基于峭度與小波包絡分析的滾動軸承故障診斷

□ 楊 晨 □ 閻樹田 □ 賀成柱 □ 馬國棟 □ 袁德強

1.蘭州理工大學 機電工程學院 蘭州 730050

2.甘肅省機械科學研究院 先進設計與制造工程實驗室 蘭州 730050

3.蘭州理工大學 數字制造技術與應用省部共建教育部重點實驗室 蘭州 730050

滾動軸承是各類旋轉機械的重要組成部件，它的運行狀態好壞直接影響到整臺機器的性能。同時也是易損部件，據統計，旋轉機械的故障有三分之一是由滾動軸承引起的，因此對滾動軸承進行故障診斷顯得尤為重要。在工況中，滾動軸承由于損傷等故障會產生沖擊振動，振動信號攜帶著軸承較全面的信息，通過采集分析振動信號來獲得滾動軸承的故障敏感特征，以達到后續精準的模式識別，振動分析法是目前應用最廣泛的故障診斷方法。

關于小波分析等方法在故障診斷中的運用，前人已經做了很多研究。文獻［1］利用小波包對振動信號進行分解重構及能量計算，提取了故障特征頻率。文獻［2］提出了結合小波包降噪與LMD的滾動軸承故障診斷方法，利用小波包去除信號中的噪聲,進行LMD分解，對故障也能有效識別。文獻［3］將峭度和小波包能量結合用在齒輪箱故障診斷，有效地實現了早期故障診斷。本文結合峭度指標、小波分解及Hilbert包絡譜分析對滾動軸承進行特征頻率的提取與識別的研究。用峭度指標直接對原始信號進行分析，可以減少誤差；峭度對沖擊脈沖類故障都比較敏感，可以明確判斷早期故障；小波分析對非平穩信號的檢測能力也很強,是實現復雜信號信噪分離的有效工具。

1 滾動軸承振動機理

滾動軸承的主要故障形式有疲勞剝落、磨損、塑性變形、銹蝕、斷裂等，當軸承元件（包括外圈、內圈和滾動體）的工作表面出現局部缺陷時,會以一定的通過頻率產生一系列寬帶沖擊,通過振動的頻率即稱為故障頻率,滾動軸承故障診斷就是要檢測這個頻率。故障特征頻率計算式如下［4］：

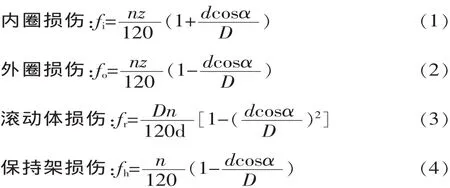
式中：d為滾動體直徑；D為節圓直徑；α為接觸角；z為滾動體個數；n為工作轉速。

對包含滾動軸承故障的振動信號進行頻譜分析,信號會在特征頻率處出現較大波峰，檢測此波峰頻率可達到監測軸承運行狀態。實際中，由于誤差等原因，故障特征頻率可能只在理論頻率或倍頻附近游動。

2 峭度指標理論應用

對于實時檢測到的振動信號直接使用無量綱峭度指標，可避免出現信號畸變和泄漏等缺陷，易于現場實現，且指標一般不受負載、轉速等變化的影響。

峭度 （Kurtosis）K是反映振動信號分布特性的數值統計量，實踐中，常用振動信號的離散數據進行分析計算，其峭度指標 K［5］為:

式中:xi為信號值；x為信號均值；N為采樣長度；σ為標準差。

設備正常運行時，峭度指標大約為3.0；若峭度指標大于3，則可判斷出現早期故障；若峭度指標非常大，則可判斷出軸承存在嚴重故障。直接根據時域指標峭度的大小和變化程度可靈敏地判斷軸承故障是否發生。但是隨著故障的進一步發展，峭度指標會下降，也不能判斷軸承故障發生的具體部位，下面將結合小波變換作進一步分析故障。

3 小波分解和Hilbert包絡分析

3.1 小波分析 ［6-7］

小波分解能夠將信號分解到一個由小波伸縮而成的基函數族上，信息量完整，且可得到各層低頻和高頻信號。這樣可以根據診斷需要選擇故障信息的頻段，進行深層處理，以便查找故障。

基本小波經伸縮、平移后形成小波函數：

式中：a為尺度參數；b為位置參數；t為時間參數；ψ為基本小波。

這樣,離散小波變換為：

3.2 Mallat算法［8-9］

在離散小波中，最常用的是二進小波變換,其快速算法稱為Mallat算法。如圖1所示，算法的實質是將原始信號f（t）通過一濾波器與一個高通濾波器分別形成近似信號與細節信號,再對近似部分進行處理，將信號在小尺度上的近似部分分解為大尺度上的近似系數和細節系數，從而保留了信號全部信息。該算法所要處理的信號是實際的連續信號f（t）經采樣得到的離散信號f（n），起始點為 A0（n）=f（n），公式為：

式中：Z為整數。

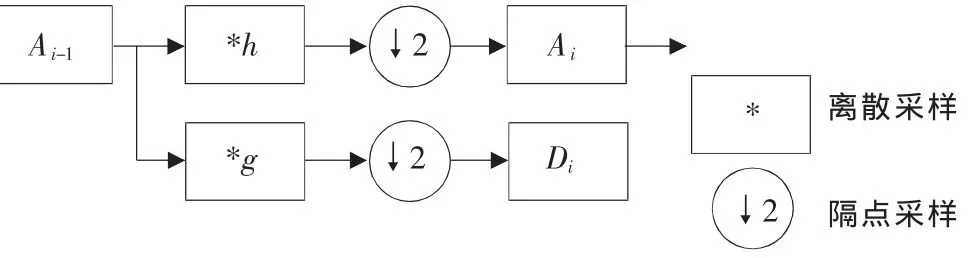
▲圖1 離散小波變換算法流程示意圖

3.3 Hilbert包絡分析

Hilbert變換是一種將時域實信號變為時域解析信號的方法。變換所得解析信號實部是實信號本身，虛部是實信號的Hilbert變換，而解析信號的幅值便是實信號的包絡。對小波處理后的包絡信號做譜分析,即可得小波包絡譜。

任意一個時間序列 g（t）的 Hilbert變換為 g（t）,數學表達為［8］：

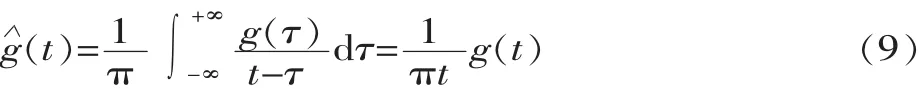
g（t）的解析信號 z（t）為：

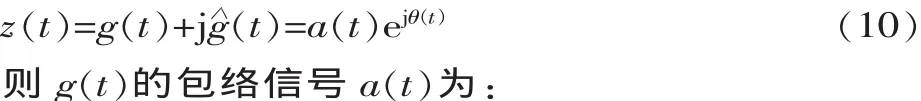
則 的包絡信號 為：

本文首先通過峭度指標計算，對滾動軸承是否出現早期故障進行判斷，若出現故障,則需對信號作進一步分析，然后選擇Db10小波進行小波分解，在通頻范圍內得到不同頻段的各層信號，消噪和消除干擾，重構各層信號，最后對能量集中的小波頻段信號進行Hilbert包絡譜分析，對照故障頻率可揭示故障類型和原因。經實驗驗證，結合峭度分析、小波分解和Hilbert包絡譜分析方法是行之有效的。

4 實驗驗證

4.1 滾動軸承實驗數據

實驗采用的滾動軸承型號為SKF6205，實驗數據來自美國Case Western Reserve University電氣工程實驗室。實驗臺包括電機、測試用軸承及傳感器等。測試用的軸承連接在電機軸上，人為地在軸承劃上電弧損傷。實驗軸承分為五組，分別為1#正常軸承、2#外圈故障、3#內圈故障、4#滾動體故障及5#保持架故障軸承。采樣頻率為12 kHz，取采樣點數8 192，轉速為1 730 r/min。 對工況中滾動軸承，根據式（1）～式（4）計算得到故障頻率，見表1。

表1 滾動軸承故障特征頻率/Hz

對1#正常軸承和2#軸承（內圈故障）進行對比分析，實時采集信號的時域波形圖如圖2所示。由圖可知，正常軸承振動信號比較平穩，當滾動軸承出現內圈故障時，信號中存在著等間隔的脈沖沖擊成分。但是由于噪聲等干擾信號,無法直接根據時域波形信號確定故障產生的原因和部位，需要更深入分析。

4.2 結合峭度指標和小波包絡譜分析

根據峭度理論，峭度指標對于沖擊脈沖類故障比較敏感。采用峭度公式對1#正常軸承信號計算其峭度，K=3.22。而對2#軸承計算，得其峭度K=5.43，明顯大于3，故2#滾動軸承確實處于故障狀態。但不能解釋故障類型和故障原因，需要進一步用小波分析。本文采用工程上常用的Db10小波對內圈故障信號進行4層小波分解。 最大觀察頻率為 6 000 Hz。 d1、d2、d3、d4分別為經Db10小波4層分解后各層的高頻系數，a4為第4層低頻系數，系數重構如圖3所示。

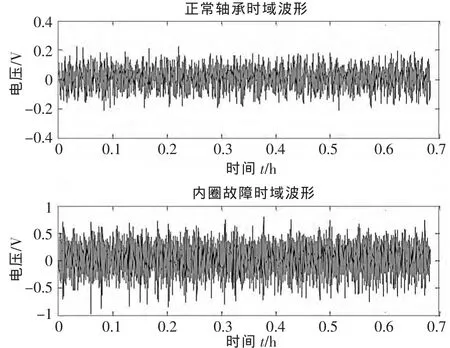
▲圖2 正常軸承、內圈故障軸承時域波形

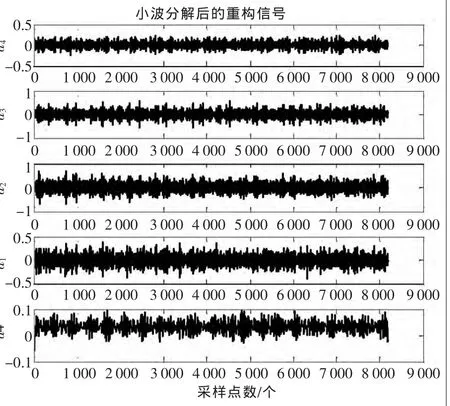
▲圖3 2#內圈故障軸承小波分解的系數重構圖

第4層小波分解低頻信號a4頻率范圍為0～375 Hz，故障能量在此頻段比較集中，故障頻率在此范圍內，故對a4重構信號進行Hilbert包絡譜分析，如圖4所示。由圖可知，Hilbert包絡譜更進一步解調細化了故障頻率的頻譜，可以看到振動信號在156.1Hz周圍存在明顯的波峰脈沖，振動能量較大，且與計算的滾動軸承內圈故障頻率也吻合，從而證實2#滾動軸承存在內圈故障。

同樣對另外的幾組故障軸承利用相同的方法進行峭度分析、小波分析及Hilbert包絡譜分析，最終也得出相似結論。一般情況對振動信號小波分解、重構頻段及包絡分析，可診斷出滾動軸承的故障。但是小波分解信號后，如何找到能量最集中、最能代表故障信號的頻段并有效提取特征具有一定技巧性。

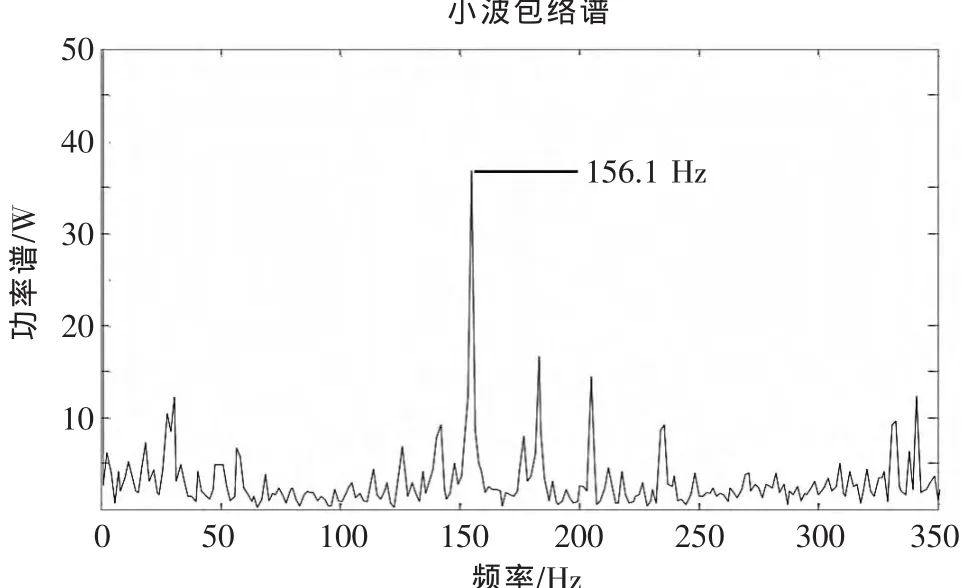
▲圖4 2#內圈故障軸承信號小波包絡譜圖

5 結束語

實際采集到的滾動軸承振動信號成分繁雜，為防止信號的畸變和泄漏等缺陷，本文直接對信號進行峭度分析判斷是否存在早期故障，同時結合處理變頻信號的有力工具——小波包絡譜，有效地提取滾動軸承故障特征頻率。通過實驗驗證，結合峭度指標、小波分析和Hilbert包絡分析的方法是一種強有力的故障診斷方法，可以有效地對滾動軸承信號進行噪聲分離、特征提取及故障識別。

［1］ 王冬云，張文志.基于小波包變換的滾動軸承故障診斷［J］.中國機械工程，2012（3）：295-298.

［2］ 孫偉，熊邦書.小波包降噪與LMD相結合的滾動軸承故障診斷方法［J］.振動與沖擊，2012（18）：153-156.

［3］ 陳水宣，鄒俊.基于峭度和小波包能量特征的齒輪箱早期故障診斷及抗噪研究［J］.機械傳動，2012（11）：9-14.

［4］ 盛兆順，尹琦嶺.設備狀態監測與故障診斷技術及應用［M］.北京：化學工業出版社，2003.

［5］ 袁云龍.基于峭度-小波包分析的滾動軸承故障診斷［J］.新技術新工藝，2008（5）：40-43.

［6］ Daubechies I.Ten Lectures On Wavelets ［M］.Philadelphia:Capital City Press,1992.

［7］ 屈梁生，張西寧，沈玉娣.機械故障診斷理論與方法［M］.西安：西安交通大學出版社，2009.

［8］ 徐玉秀，原培新，楊文平.復雜機械故障診斷的分型與小波方法［M］.北京：機械工業出社，2003.

［9］ Mallat S.A Theory for Multiresolution Signal Decomposition:The Wavelet Representation ［J］.IEEE Transactions Pattern Analysis and Machine Intelligence，1989，11（7）:674-693.