基于改進相關系數聚類法的股票投資組合研究

溫 權 陳 茜 劉力一

（中國人民大學商學院 北京 100872）

一、引言

最優股票投資組合選擇及其風險控制一直是資本市場研究的熱點問題。已有文獻對資產組合最優決策理論進行了大量研究，在資產組合選擇與最優配置、資產組合規模效應與影響因素、以及資產組合風險度量與控制等重要問題取得了豐碩成果。但遺憾的是，無論是理論還是實證研究都很少考慮到金融時間序列的時變性、聚集性、持續性等波動特征對資產組合風險規避與控制的影響。而本文正是針對目前研究的不足，通過對滬市A股的120支股票收益率進行擬合使用改進的相關系數法對股票收益波動時間序列相關性進行匹配，聚類，從而優化了股票投資組合選擇的方法。并通過實證研究，證明了在哈里?馬柯威茨證券組合評價標準下，使用該種股票投資組合選擇方法，可以獲得同等收益水平下，更低風險的股票投資組合，從而為投資者選擇合理的股票投資組合提供了可能的方法。

二、文獻綜述

（一）國外文獻 馬柯威茨于1952年最早提出了均值-方差理論，成為現代投資組合理論的開山鼻祖。自此之后，很多金融學者在前人的研究基礎上對該理論進行了補充和發展，如托賓（1958）在提出了著名的兩基金分離定律：當存在無風險資產的情況下，有效前沿上的任意一點都可以表示為（無風險利率，0）和切點的線性組合。此外，大批學者踏上了簡化計算，完善模型的征程。一是盡可能的減少模型計算量，例如：夏普（1963，1964，1970）提出了單因素模型，它的主要思想是：市場的總體因素統一作用于所有股票，市場以外的因素只作用于某一只股票，因此可以通過股票組合來分散。單因素模型使用β來衡量投資組合的風險。提高了人們對市場行為的了解。羅斯（1976）提出了套利定價理論。該理論認為在市場均衡時沒有套利機會，因此承擔相同風險因素的投資組合應該具有相同的期望收益率。二是開發新的投資組合模型。例如Mao（1970）提出了均值-下半方差模型。Speranza（1993）提出半絕對風險偏差函數。J.P Morgan提出的基于Var的風險度量系統等，至今這個風險度量系統還在很多金融機構被廣泛使用。

（二）國內文獻 我國對金融市場研究起步較晚是一個現實，這是由于很多客觀因素造成的。近幾年中，我國學者也對投資組合理論進行了深入的研究。唐小我（1994）針對我國證券市場的賣空限制情形下的投資組合模型進行了研究。王春峰、屠新曙和厲斌（2002）運用了幾何方法解決投資組合問題。徐緒松、楊小青和陳彥斌（2002）提出了“半絕對離差風險測量工具”。劉小茂、李楚林和王建華（2003）研究了在正態情形下，風險資產組合的均值-CVaR邊界，并與方差風險下的均值-方差邊界進行了比較。陳金龍和張維（2002）分析了投資組合與CVaR之間的關系。此外，安起光、王厚杰（2006），劉慶富（2006），榮喜民、武丹丹和張奎廷（2005）、劉志東（2006）等學者在組合預測和方法領域獲得了顯著的理論成果。

三、研究設計

（一）研究思路 本文選取了馬柯威茨的均值-方差模型作為本文的理論依據，該模型評價投資組合的標準，是當收益一定時風險最小，或者當風險一定時收益最大。該模型的思想是選取相關性低的投資工具進行組合來分散風險，從而得到更好的投資收益。因此如何衡量股票相關性，并進而篩選出相關性低的投資組合成為該模型的關鍵。由于之前的研究，無論是理論還是實證都很少考慮到金融時間序列的時變性、聚集性、持續性等波動特征對資產組合風險規避與控制的影響。而本文正是針對目前研究的不足，通過使用改進的相關系數法衡量股票收益波動時間序列的相關性，并據此聚類，優化了股票投資組合選擇的方法。具體的思路如下：

（1）股票收益波動性擬合。對于金融時間序列分析，常常會出現某一特征的值成群出現的情況。如對股票收益率序列建模，其隨機擾動項往往在較大幅度波動后緊接著較大幅度的波動，在較小幅度波動后緊接著較小幅度的波動，這種性質稱為波動的集群性。在一般回歸分析中，要求隨機波動項是同方差，但這類序列隨機擾動項的無條件方差是常量，條件方差是變化的量。所以需要使用自回歸條件異方差模型（ARCH）或者廣義自回歸條件異方差模型（GARCH）。

（2）時間序列相似性度量。測量時間序列相似性的方法有很多，最主要使用的是歐式距離法和相關系數法。歐式距離法的優點是計算簡單，易于理解，但是它容易受到序列波動性的影響，而且當序列長度增加時，其距離也會增加。特別是當時間軸發生伸縮或彎曲時，就不能夠準確測量序列的相似性了。而相關系數法的優點是計算量少，而且即使兩個序列均值不同，也能夠準確比較相似性，而在歐式距離法中，如果兩個序列均值不同，即使它們是相似的，計算出來的距離仍然會很大，從而誤導了結果。但是相關系數法也存在其局限性，它只適用于長度相同的序列,因此在比較長度不同的時間序列時，需要改進該方法，改進的相關系數法如下。設有兩只股票P和Q，長度為m的收益波動序列分別為X和Y：X=（x1，x2，…，xm-t，xm-t+1，xm）；Y=（y1，y2，…，ym-t，ym-t+1，ym）。首先要在X和Y中截取長度相同的兩個子序列，設長度為t，最好從序列最鄰近當前時段開始截取，t不宜過短，計算子序列X1=（xm-t+1，xn）和Y1=（ym-t+1，yn）的相關系數r1：r1=將子序列的長度向前增加一個，即長度為（t-1），計算X2=（xm-t，xm-t+1，xm）和Y2=（ym-t，ym-t+1，ym）的相關系數：r2=，重復上述步驟，依次類推，直到子序列包含全部序列的長度m，計算出的相關系數有（m-t+1）個。

將計算出的全部相關系數進行平均，則得到的為改進的相關系數：r~=。由于聚類需要使用距離，而改進的相關系數r~是屬于［-1,1］，所以要將~r轉化成大于等于零的距離，另d=|~r-1|，則d∈［0,2］。通過d對股票進行聚類。

（3）股票聚類。聚類分析。方法中最常用的是分層聚類。分層聚類方法是通過一系列或者是相繼的合并，分割來進行的。是從單個對象開始，這樣在開始時每一個對象都是一類，將那些最相似的對象首先分組，然后將組與組根據它們之間的相似性進行合并，最后隨著相似性不斷下降，所有的組漸漸融合成為一個聚類。

（4）確定最小方差資產組合集合的方法。常用的投資策略優劣評估標準有：收益率分布形態指標，夏普比率，風險價值（VAR），條件尾部期望（CTE）等。本文將主要使用由馬柯威茨于1952年提出的用圖像分析法確立風險資產的最小方差組合集合和有效邊界的過程。我們以只擁有三個資產的組合為例。利用圖像法建立最小方差資產組合集合的過程，就是在以資產權數為坐標軸的空間內，繪制反映資產組合各種預期收益和風險狀況的線，然后依理性投資者選擇資產和資產組合的原則確定最小方差資產組合集合的過程。我們分析是在允許賣空的前提下，以便不受限制條件的約束。假設我們對資產A，B，C進行組合，已知E（rA）=10%，E（rB）=20%，E（rC）=30%，設A，B，C資產的權數分別由xA，xB，xC表示，限制條件為xA+xB+xC=1，由于xC=1-xA-xB，因此只要知道xA和xB的數據，就可以得到xC的數據。因此，可以在一個二維平面圖上顯示三個資產的組合情況，同理，可以使用（n-1）維圖顯示n種資產的組合。在以xA，xB為坐標軸的圖形中，直線AB的方程式是xA+xB=1，所有僅投資A和B資產，不投資C的資產組合都分布在這條線上；不包括A的組合都分布在B軸上，同理，不包括B的都分布在A軸上，分布在AOB三角形區域內的各種資產組合都不含賣空資產，在AOB以外的資產都含有一種或者兩種資產的賣空。根據具體的限制條件在坐標圖上的某個區域進行查找，以確定最小方差的資產組合。而這個過程可以通過EXCEL線性規劃的方式實現。

（二）樣本選擇與數據來源 本文選取的研究對象為2008年1月1日到2009年12月31日在上交所交易的，代碼為sh600000-sh600120的A股股票，數據來源為國泰安數據庫。剔除掉缺失值，實際得到102只股票。分別計算這102只股票的日收盤價數據個數，其中最多的為488個數據，以488為基準，凡是數據個數小于（不包括等于）基準數據15個以上的股票都被清除。這樣經過清除后，剩下83只股票。然后對這83只股票的缺失值進行修補，修補的原則是以前一天的收盤價代替缺失值，經過修補后，每只股票都有488天的數據。計算每只股票的日對數收益率，公式為：日對數收益率=log（當日收盤價）-log（前日收盤價）。經過計算，每只股票都有487個日對數收益率，

（三）時間序列分析建模過程 首先需要對得到的股票對數收益率進行建模，以單只股票序列為例，過程如下：（1）做統計圖觀察判斷。（2）單位根檢驗。序列大致可分為有三種：擴散型序列，單位根型序列和平穩序列。在實際問題中，時間序列大多并不平穩，而是呈現出各種趨勢性和季節性。由于在實際生活中擴散型序列比較少見，很少作為理論研究的對象，所以我們判斷的基礎就建立在單位根型序列和平穩序列上。做單位根檢驗的目的就是要區分二者，對單位根型序列做差分處理，去除趨勢性因素，從而得到平穩序列。（3）確定時間序列主模型。對原序列進行差分處理，得到寬平穩序列，求解它的自相關系數，偏自相關系數，同時觀察自相關和偏自相關圖像，確定ARMA（p，q）階數。由計算機程序，生成主模型系數的參數估計，得到相應的殘差序列。（4）根據股票對數收益率數據畫散點圖，趨勢圖，觀察序列是否屬于平穩序列，是否具備集群性，直觀地判斷是否可以采用條件異方差模型擬合數據。（5）ARCH效應檢驗。ARCH模型通常用于回歸模型：yt=x'tβ+εt。若隨機干擾項εt不存在ARCH效應，則可以直接對模型作最小二乘估計；若εt存在ARCH效應，則應找到ARCH模型的形式，即在上式中附加εt=·vt，并確定q，再進行參數估計。對序列進行ARCH效應檢驗的最常用方法是拉格朗日乘數法即LM檢驗。假設εtARCH（q），則可以建立如εt=·vt的輔助回歸模型：ht=α0+α1εt-12+…+αqεt-q2

原假設：H0：α1=…=αq=0；備擇假設：H1存在αi≠0，1≤i≤q；檢驗統計量：LM=nR2～X（2q）

其中，n為計算輔助回歸時的樣本數據個數，R2為輔助回歸的未調整可決系數，即擬合優度。檢驗標準。根據輔助回歸ht=α0+α1εt-12+…+αqεt-q2的最小二乘估計，得到擬合優度R2，由LM=nR2～X（2q）計算檢驗統計量LM，根據給定的顯著性水平α和自由度q查x2分布表，得到相應的臨界值xα2（q）或原假設成立的概率，則可得到結論。LM＞xα2（q），拒絕H0，表明序列存在ARCH效應；LM＜xα2，不能拒絕H0，表明序列不存在ARCH效應。當階數需要取一個很大的值時，可以考慮GARCH模型。（6）對殘差序列建立模型。根據上一步效應檢驗的結果，使用理論部分講述的條件異方差模型對殘差序列建立模型。（7）模型的檢驗。這一步是通過對模型殘差序列et檢驗是不是白噪聲，考核所建模型的優劣。也就是說，如果經檢驗et是白噪聲序列，模型是合理的，可用于預測，否則，應進一步改進模型。所謂白噪聲序列就是一個各項之間互不相關的純隨機序列。（8）提取結論所需的條件方差數據。根據模型求得條件方差，此列數據就是目標數據：收益率波動性的擬合估計數據。用方差度量刻畫了投資組合的整體風險。

表1聚類過程表

四、實證檢驗分析

（一）投資組合收益波動性擬合 根據上文的時間序列分析擬合步驟，使用S-PLUS軟件中finmetrics的模塊，Excel規劃求解，VBA，SAS，R軟件共同完成從數據的整理，預處理，分析到得出結論，并配以圖形的表達來完成對投資組合風險的度量。

（1）ARCH效應檢驗及股票再篩選。對收益波動率的估計本文使用動態波動率估計模型。在使用GARCH類模型對股票收益的波動率進行擬合之前需要再對選入研究的股票做一次篩選。通過ARCHTEST對這83支股票進行檢驗。在0.05的顯著性水平下通過檢驗說明該股票的收益率波動性具有集群性，也就是說收益率是變換的，使用ARCH或GARCH模型擬合更加合理。共有33支股票的收益率數據經過了ARCH效應檢驗。

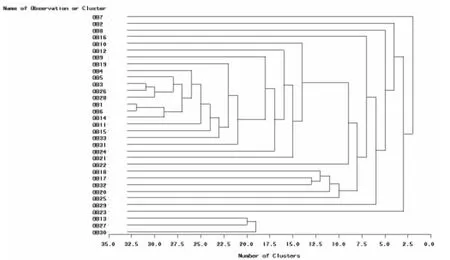
圖1 33支股票聚類過程圖

（2）股票收益波動性擬合。對這33支股票分別進行收益波動性擬合。第一次采用ARMA模型作為主模型對收益率數據進行建模，然后對殘差進行GARCH模型擬合，雖然擬合后殘差序列均通過了檢驗，但在相似性聚類中效果不佳。于是重新選定主模型。將常系數模型作為主模型，然后對殘差進行GARCH模型擬合，殘差也均通過了檢驗。在模型中，條件方差序列就是待求的股票收益波動性序列，最后得到33條各488個數據的波動率序列。GARCH（p，q）的最簡單形式GARCH（1，1）。該過程可以表示為：

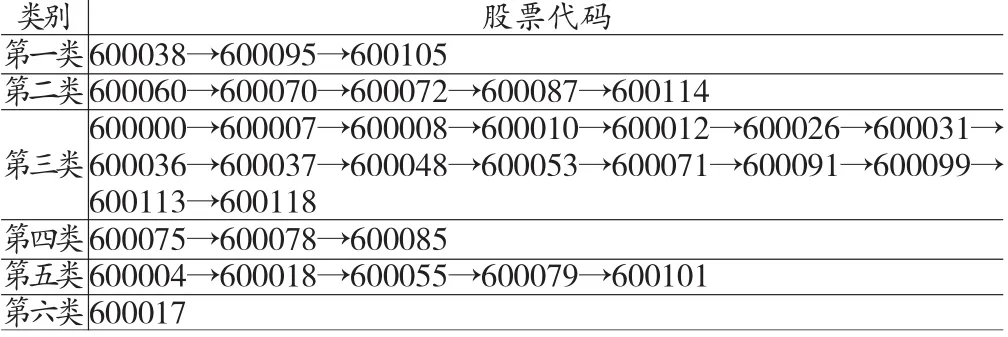
表2 33支股票聚類結果

其中，｛v｝t獨立同分布，且vt～N（0，1），參數滿足α0＞0，β1≥0，α1≥0。εt～GARCH（1，1）是穩定過程的成分必要條件為α1+β1＜1。

（二）采用改進的相關系數法比較股票收益波動性的相似性

計算33支股票中任意兩支股票的相似性。設任意兩支股票A、B：A=

由于股票收益波動序列是兩年期的日數據，因此首先選取時間期為2008年1月2日-2008年12月31日長度為245的兩個子序列A1、B1：

計算A1、B1的相關系數記為r1。之后將序列的起點向前推一個，計算時間期為2008年12月28日-2009年12月31日長度為246的兩個子序列A2、B2：

計算A2、B2的相關系數記為r2。繼續按照這種方式，每次將子序列的起點向前推進一期，計算相同時間期的兩個子序列之間的相關系數，直到最后一次計算A、B序列全部數據之間的相關系數r242。總共可以得到242個相關系數。最后，將所得的全部相關系數的均值作為A、B序列間改進的相關系數r*AB：r*AB=

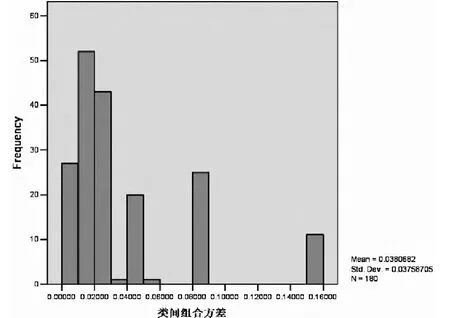
圖5 類間組合方差圖

相關系數的取值范圍在［-1,1］之間，系數為正，說明兩支股票收益率的波動性之間成正相關，系數越大，相似度越高；系數為負，說明兩支股票收益率的波動性之間成負相關；系數為零，說明兩支股票收益率的波動性之間不相關。

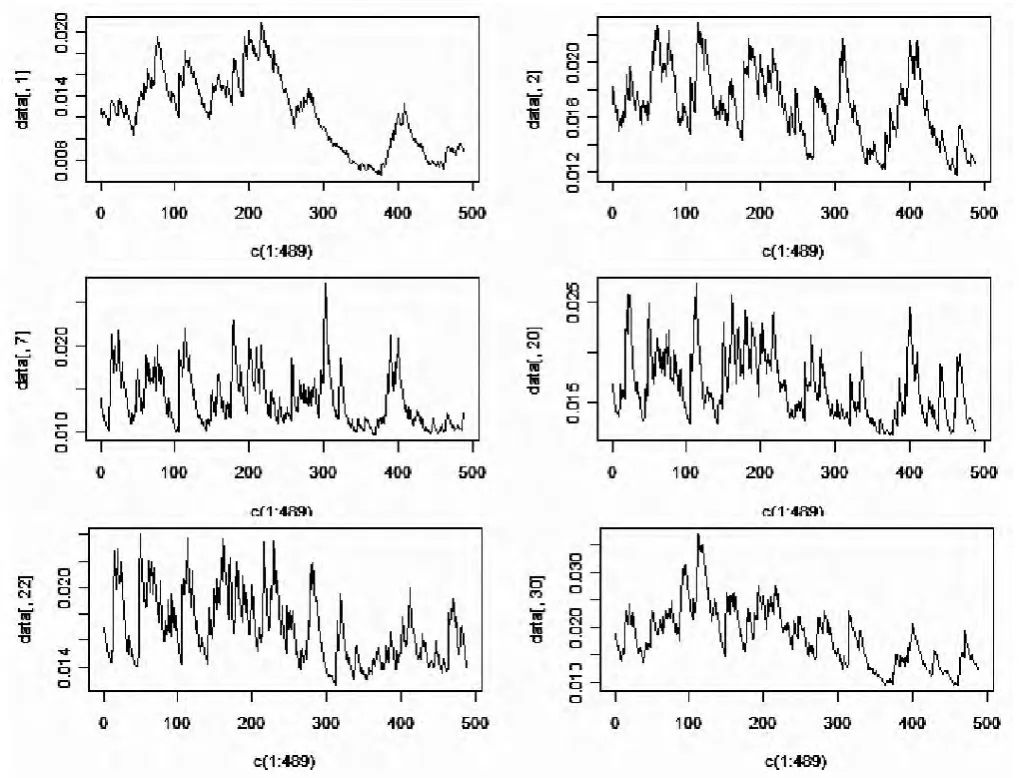
圖2 六類股票收益波動序列圖

（三）股票聚類 為了將A、B之間的相關系數轉化成距離，還需計算|r*AB-1|，記為dAB，即 dAB=|r*AB-1|

全部股票經過點間距計算，可以得到33×33的距離矩陣。由于篇幅限制，這里不做展示。將距離矩陣輸入到SAS軟件當中，借助軟件的聚類方法，采用Agglomerative算法，選擇method=density，K=2可以得到聚類結果。這里所用的類間距估計法是最近鄰密度估計法。軟件輸出的聚類過程及結果如表（1）和圖（1）所示，可以看出33支股票被聚為6類，具體分類情況如表（2）所示。這六類股票的收益波動率序列存在很大差異，從每一類中選擇一個典型的序列收益波動率圖，展示結果如下。

（四）投資組合績效比較 為了驗證改進的相關系數聚類法在股票投資組合中的應用效果，使用的主要方法是將基于使用改進相關系數聚類法根據收益率相似性聚類的股票投資組合與隨機組合、類內組合對比，比較在相同收益率水平下，組合的最小方差值大小。該值越小，說明該組合績效越好。具體來說，投資組合績效比較的研究思路為：首先確定組合收益率的大小，其次確定每種組合方案下抽取組合樣品的個數，然后分別計算每種方案下的組合風險均值，最后將三種方案下組合風險的均值進行對比得出結論。

表3 三種組合方式下可能的組合種類

（1）確定收益率大小。在計算組合的風險之前需要首先確定組合收益率的大小。由于所選數據是2008-2009年間的股票數據，而這段時期內股市處于衰退的狀態，眾多股票長期出現負收益率，因此將組合的收益率設為較小的數值，假設為0.03。

表4 EXCEL中規劃求解功能的設置

表5 三種組合方式的平均最小方差值

（2）確定三種組合方式的抽樣方案。確定三種組合方式的抽樣方案時要首先計算出每種組合方式下可能出現的組合的種類。如表（3）所示，隨機組合的種類最多，基于相似性聚類的組合次之，類內組合的數目最少。為了能比較出組合的績效，規定每種組合方式下抽取180個樣品計算風險均值。根據它們各自組合的特點，可以采用不同的方式來選取樣品。基于相似性聚類的組合在選取樣品時可以采用類似分層抽樣的方法，將不同類別作為不同層看待，從每一層中隨機抽取一支股票。每一次抽取完畢，可以得到6支股票，將這6支股票作為一個組合。按照這種方式抽取180個組合即可。隨機組合在選取樣品時按照統計中排列組合的方式，隨機從33支股票中無放回地抽取6支，作為一個組合。按照這種方式抽取180個組合即可。類內組合在選取樣品時先將可能的組合種類列出，然后按照簡單隨機抽樣方式從這8008個待抽樣品中抽取180個組合即可。

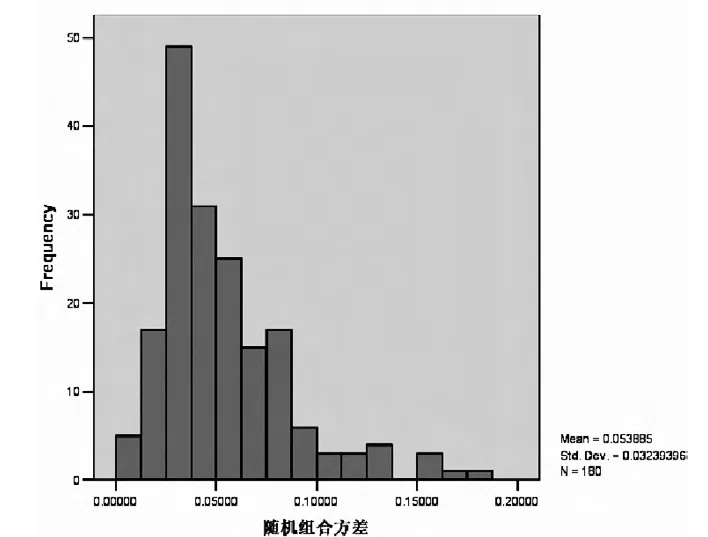
圖3 隨機組合方差圖

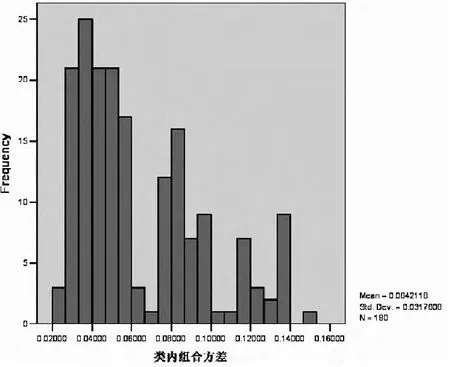
圖4 類內組合方差圖

（3）計算三種組合方式的風險。計算不同組合方式的風險大小時主要通過EXCEL軟件中規劃求解的功能來完成。相應的指標設置如表（4）所示。通過計算就可以得到滿足條件的有效組合的最小方差值。由于篇幅所限，每種組合方式下的樣本方差計算結果不在此列示。

（4）比較三種組合方式的風險。通過均值計算，很容易得到每種組合方式下平均最小方差值，如表（5）所示。可以看出，基于股票收益率波動性的相似性聚類的組合在確定的收益率下獲得了比隨機組合、類內組合更小的最小方差值。另外，從圖（3）到圖（5）中對于不同組合方式下的實驗結果進行觀察，發現在基于相似性聚類的組合方式下180次試驗結果的方差很小，也就是說每次實驗得到的最小方差值十分相近。這些現象說明采取基于相似性聚類的組合方式不僅可以更有效地降低風險，而且在這種組合方式下獲得的最小方差值更具穩定性。

五、結論

本文研究的重要意義在于它以資產組合整體為對象和基礎，以擁有整個資產組合投資者的效用最大化為目標所進行管理。股票組合研究是有其必要性的，首先構建股票組合可以降低投資風險，如同將雞蛋分放在不同的籃子中一樣；其次股票組合可以實現收益最大化，就單個股票而言，風險與收益成正比，高收益總伴隨著高風險，但是，各種不同的股票以不同比例組合起來，就可以使證券組合整體的收益-風險特征達到在同等風險水平下收益最高和在同收益水平下風險最小的理想狀態。經過文章的分析和研究，得到了如下結論：本文運用一個新的方法，使用改進的相關系數法對股票收益波動率進行擬合，并據此對股票進行聚類，然后通過比較隨機，類內兩個參照組的方差，得出在相同收益率下，使用該方法獲得的收益波動性差異大的股票組合可以獲得更低的風險系數。當今社會，資產價格波動和投資管理的歷史使人們認識到憑借資產價格預測來進行投資管理是不可靠的，還是應該把重點放在科學地選擇資產，確定最佳組合上。本文為投資者，研究者都提供了一種選擇股票投資組合的新路徑。

［1］陳湘濤、李明亮、陳玉娟：《基于時間序列相似性聚類的應用研究綜述》，《計算機工程與設計》2010年第3期。

［2］勞艷清：《我國企業年金基金投資組合研究》，《廣東外語外貿大學碩士學位論文》2008年。

［3］李俊奎：《時間序列相似性問題研究》，《華中科技大學碩士學位論文》2008年。

［4］管河山：《金融多元時間序列挖掘方法研究與應用》，《廈門大學博士學位論文》2008年。

［5］許星劍：《全國社會保障基金股票投資組合績效評價與實證研究》，《哈爾濱工業大學碩士學位論文》2008年。

［6］普繼平、馬永開：《我國證券市場中基金組合風險與組合規模關系的實證分析》，《電子科技大學學報》2005年4期。

［7］王玲玲：《證券投資組合優化模型的研究》，《華中師范大學碩士學位論文》2008年。

［8］高鑫生：《現代投資組合理論對中國資本市場適用性的實證研究》，《天津財經大學碩士學位論文》2009年。