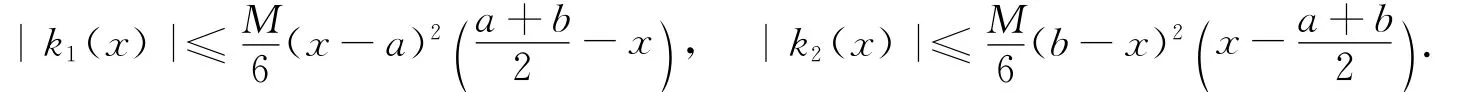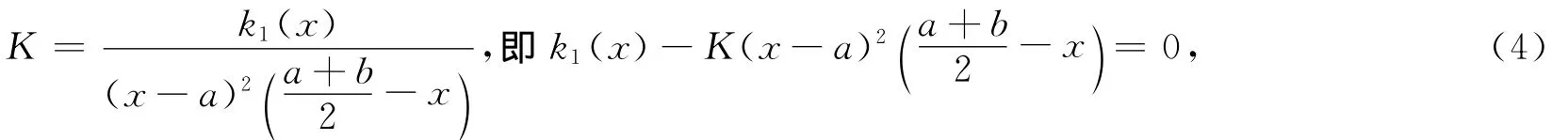關于h凸函數(shù)的加權(quán)三點不等式

時統(tǒng)業(yè)，吳 涵，宋祥斌

（海軍指揮學院 浦口分院，江蘇 南京 211800）

Simpson不等式在計算定積分的數(shù)值計算中有著重要的作用.近些年來，許多學者針對被積函數(shù)的各種情形，利用被積函數(shù)的各階導數(shù)估計求積公式的誤差.本文針對三階可微函數(shù)，通過建立關于積分的恒等式，在三階導函數(shù)的絕對值是h凸函數(shù)的情形下，利用簡單的數(shù)學分析方法和H?lder不等式，給出若干帶有權(quán)函數(shù)的三點不等式，并在特殊情況下得到有關文獻的結(jié)果.

1 預備知識和引理

關于Simpson不等式的各種改進和推廣，可參見文獻［1－9］.文獻［7－8］分別對其三階導函數(shù)的絕對值是m凸函數(shù)和第二種意義上的s凸函數(shù)的可微函數(shù)建立了一些Simpson型不等式.

定義1［10］設h：J?R→R是取正值的函數(shù)，f：I?R→R是非負函數(shù)，且對于任意x，y∈I，t∈［0，1］，有f（tx＋（1－t）y）≤h（t）f（x）＋h（1－t）f（y），則稱f是h凸函數(shù).

關于h凸函數(shù)的性質(zhì)和不等式可參見文獻［9－16］.文獻［9］考慮了三階導函數(shù)的絕對值是h凸函數(shù)的可微函數(shù)，建立了一些Simpson型不等式，推廣了文獻［8］的結(jié)果.

定理A［9］設h：J?R→R（［0，1］?J）是非負函數(shù)，f：I?［0，∞）→R是int I上的三階可微函數(shù)，a，b∈int I，a＜b，f（3）∈L1［a，b］.若｜f（3）｜是［a，b］上的h凸函數(shù)，則有

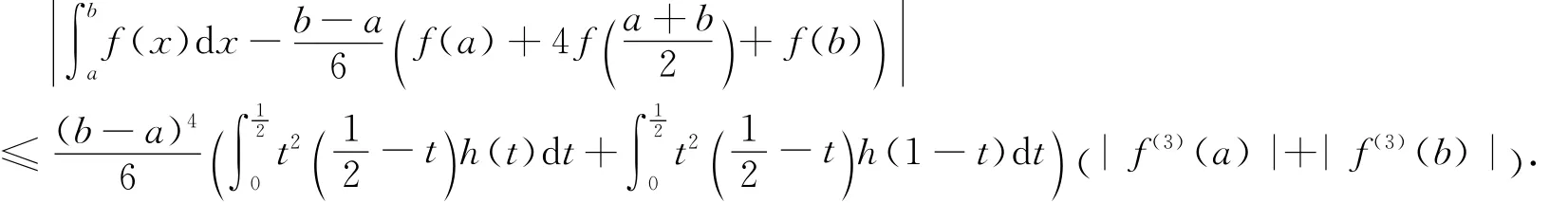
定理B［9］設h：J?R→R（［0，1］?J）是非負函數(shù)，f：I?［0，∞）→R是int I上的三階可微函數(shù)，a，b∈int I，a＜b，f（3）∈L1［a，b］.若｜f（3）｜q是［a，b］上的h凸函數(shù)，且，則有

定理C［9］設條件同定理B，則有

為了建立證明本文主要結(jié)論所用引理，引入函數(shù)k（x），并考慮其簡單的性態(tài).假設g：［a，b］→R是正的可積函數(shù)，定義

其中

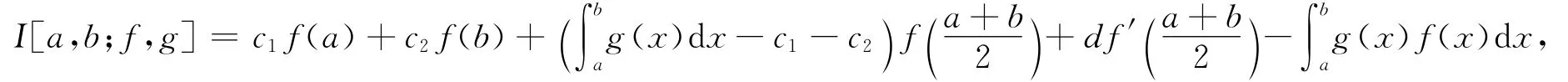
其中c1和c2如（2）式所定義，

引理1 設f：I?R→R是int I上的三階可微函數(shù)，a，b∈int I，a＜b，f（3）∈L1［a，b］，g：［a，b］→R是正的可積函數(shù)，k（x）由（1）式所定義，則有

證 由分部積分法易證得，過程略.

引理2 設g：［a，b］→R是正的可積函數(shù)，k1（x）和k2（x）如（1）式所定義.若g≤M，M 為正常數(shù)，則有

2 主要結(jié)……

登錄APP查看全文

猜你喜歡

定義利用

利用min{a，b}的積分表示解決一類絕對值不等式

中等數(shù)學(2022年2期)2022-06-05 07:10:50

永遠不要用“起點”定義自己

海峽姐妹(2020年9期)2021-01-04 01:35:44

定義“風格”

VOGUE服飾與美容(2020年9期)2020-09-02 14:47:26

利用一半進行移多補少

小學生學習指導(低年級)(2020年6期)2020-07-25 02:31:36

利用數(shù)的分解來思考

小學生學習指導(低年級)(2018年9期)2018-09-26 05:59:44

Roommate is necessary when far away from home

瘋狂英語·新讀寫(2018年2期)2018-09-07 09:32:10

成功的定義

山東青年(2016年1期)2016-02-28 14:25:25

修辭學的重大定義

當代修辭學(2014年3期)2014-01-21 02:30:44

山的定義

公務員文萃(2013年5期)2013-03-11 16:08:37

教你正確用（十七）

海外英語(2006年11期)2006-11-30 05:16:56

江蘇師范大學學報(自然科學版) 2014年3期

江蘇師范大學學報(自然科學版)的其它文章

非精確線搜索條件下共軛梯度法的收斂性分析

我國區(qū)域文化產(chǎn)業(yè)競爭力水平與格局研究

江蘇省制造業(yè)空間格局及其變化分析

2，4－二羥基 －3，5－二氯苯乙酮的微波合成及晶體結(jié)構(gòu)

類Mg離子的電子關聯(lián)效應研究

偏心拉桿極值應力的電測法研究