稠油集輸伴熱管道軸向溫度場數(shù)值模擬算法研究

陳春，徐太貴，杜培楠，李博，劉漢強，姜帥, 陳飛，寶月

（1. 中國石油大學（北京），北京 102249； 2. 中國石油集團東南亞管道有限公司，北京 100083；3. 中原油田分公司油氣儲運管理處，河南 濮陽 457165; 4. 常州大學，江蘇 常州 213016）

我國稠油資源分布廣泛，預計資源量達300′ 108t。隨著陸上大多數(shù)主力油田進入“雙高”（高采出程度、高含水率）和產量遞減階段，加大對稠油資源的開采力度，必將成為我國能源領域的發(fā)展趨勢[1]。在稠油集輸?shù)倪^程中，常采用熱水外伴熱的方式對其進行加熱，以降低粘度，保證其流動性能。由于稠油具有密度大，粘度高，流動性差的特點，每年集輸系統(tǒng)中動力和熱力消耗巨大[2]。同時，在對稠油伴熱系統(tǒng)進行設計時，使用的熱力和水力分析方法通常偏于保守，造成了一定的浪費。本文對稠油伴熱系統(tǒng)溫度場數(shù)值模擬提出了新的方法，為稠油伴熱系統(tǒng)水力熱力耦合求解奠定基礎。

1 物理問題描述

將熱水管道、稠油管道以及管道與保溫層間的空氣分別看做溫度均勻介質，求解能量方程可以得到稠油伴熱系統(tǒng)的溫度場初步分布結果，但是此結果不夠精確。在此初步計算的結果之上確定某一管段的熱水溫度，可以將熱水溫度與伴熱系統(tǒng)外界空氣溫度作為邊界條件，求解稠油溫度。求解過程的難點在于：①管段內熱水溫度固定后，可將熱水看做非流動狀態(tài)，然而稠油處于流動狀態(tài)，不能將稠油的導熱看做簡單的穩(wěn)態(tài)問題；②鋼管與空氣及保溫層處于靜態(tài)，其導熱為穩(wěn)態(tài)過程，欲得到稠油溫度場，兩者需要耦合求解。

2 數(shù)學模型建立

為求解此物理問題，需將其做必要簡化：①忽略系統(tǒng)內稠油管道、熱水管道與防腐層間的空氣自然對流換熱，看做簡單的熱傳導；②忽略兩種介質之間的接觸熱阻。表1為符號說明。

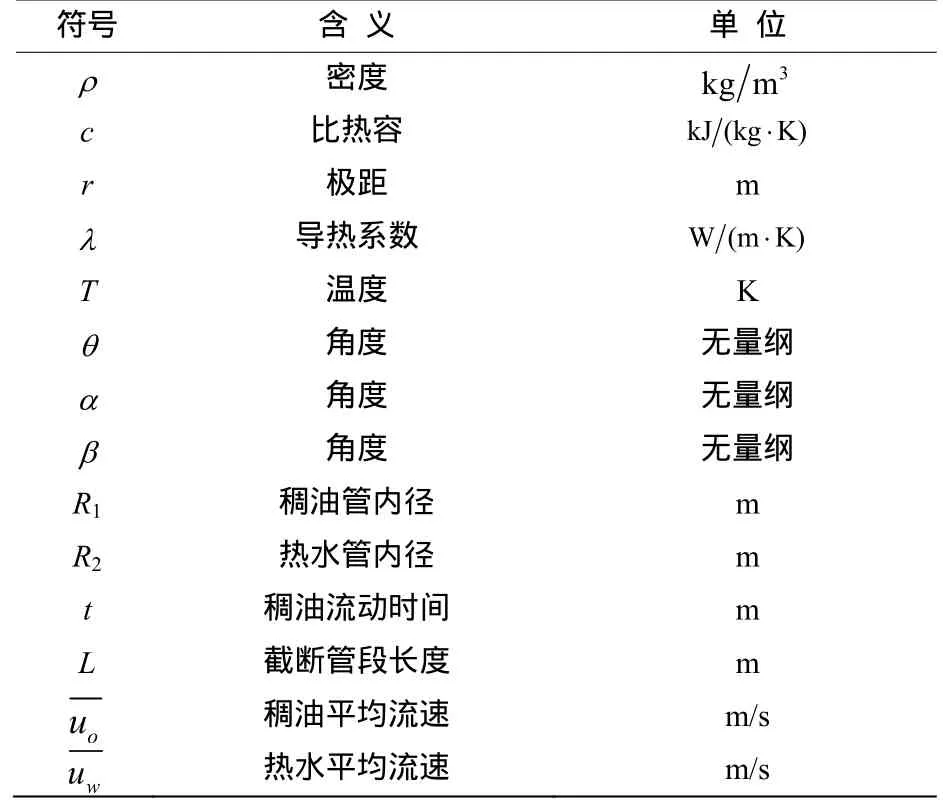
表1 符號說明Table 1 Explanation of symbols

由于計算區(qū)域的不規(guī)則性，在極坐標下求解此物理問題。下面給出稠油伴熱系統(tǒng)徑向導熱過程的數(shù)學模型。能量方程如下式：

3 網絡劃分

結構化極坐標網格的實施主要涉及參數(shù) 與參數(shù) 的計算，由于計算區(qū)域關于x軸對稱，故劃分網格時，只需劃分x軸上方區(qū)域，將區(qū)域分為三部分：BOF，AOB，EOA，如圖1所示，其中，A、B、C、D為切點。

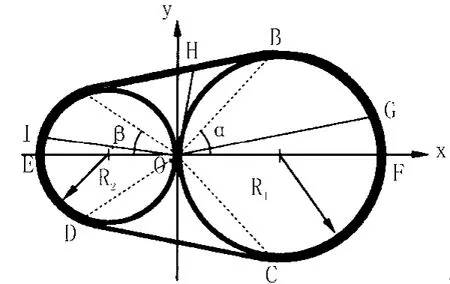
圖1 網格劃分參數(shù)函數(shù)關系示意圖Fig.1 The schematic of mesh parameter function

通過角度的大小來識別三個區(qū)域，通過數(shù)學推導，可得：

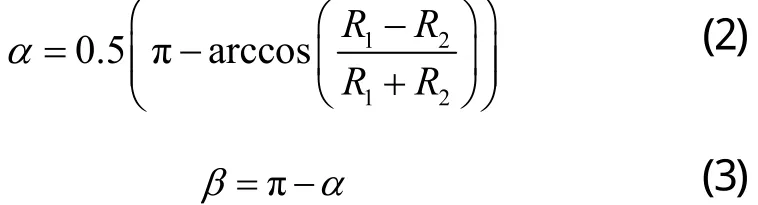
對應三個區(qū)域的極距的計算函數(shù)，例如，OG、OH、OI，計算函數(shù)為：

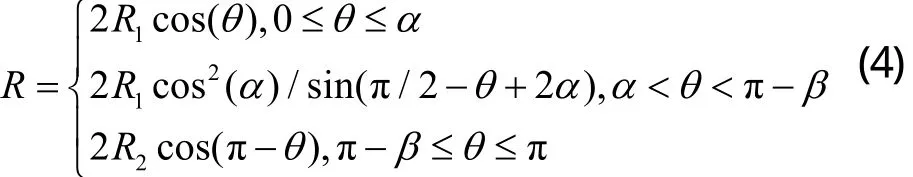
按精度需求將極軸旋轉一周 2π角度分成 Nq份，將極距分成Nr份，參考文獻[3]做法，并將保溫層區(qū)域、管壁區(qū)域加密，進行計算區(qū)域的網格劃分。通過函數(shù)控制將網格分為保溫層、空氣、管道、熱水以及稠油五個部分。

為了實施有限容積法，需求得各個節(jié)點的控制容積，由于計算區(qū)域不規(guī)則，控制容積的計算比圓形計算區(qū)域極坐標網格、直角坐標系均分或非均分網格復雜得多，針對三個不同的網格劃分區(qū)域，分別推導控制容積的計算公式，得到不同節(jié)點的控制容積，并可知遠離極點處節(jié)點的控制容積大，網格加密處節(jié)點控制容積小，符合網格特點。使用函數(shù)控制將保溫層、空氣、管道、熱水以及稠油五部分抽離出來，區(qū)域面積的相對偏差為0.013%，符合精度要求。

4 方程離散

對保溫層、空氣、管道、熱水以及稠油的導熱方程(1)在極坐標控制容積上進行離散,為保證物理問題的物理意義，需將物理平面映射到計算平面中去，來實施有限容積法[4]。

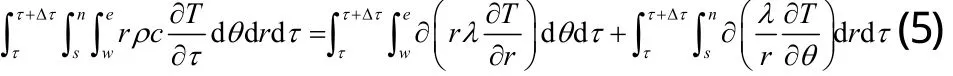
將上式整理成通用的離散化方程形式：

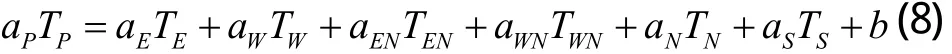
式中各符號含義和關系如圖2所示。

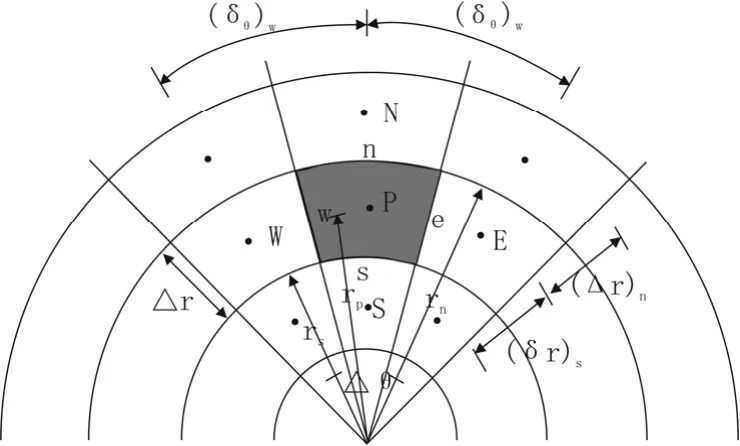
圖2 離散參數(shù)示意圖Fig.2 The schematic of discrete parameters

5 方程求解

圖3 問題簡化模型Fig.3 The simplified model

綜上所述，稠油溫度的求解轉變?yōu)橐韵聠栴}：以長度L的熱水管段截面上的平均溫度作為第一類邊界條件，以及伴熱系統(tǒng)外界空氣溫度作為第三類邊界條件，求解稠油截面上溫度分布，此問題為非穩(wěn)態(tài)導熱問題，非穩(wěn)態(tài)過程的總發(fā)展時間為采用高斯-賽德爾求解器進行求解，求解過程中處理的兩個難點及解決方案如下：

(1)難點1：極坐標奇點的處理方法

極坐標下劃分網格求解物理問題，按照有無奇點可將網格分為兩類。奇點形成的原因為：當極坐標的極點被包含在計算區(qū)域內時，極點周圍的控制容積由矩形退化為三角形，且極點被周圍的三角形控制容積所共有。

目前，對于奇點的處理有：線性差分和能量守恒等方法[5]。本研究采用符合物理意義的分塊線性差分方法，奇點為水管與油管的切點處，在奇點處熱量由水管傳向油管，水管溫度高于油管，因此將奇點一分為二，一個使用油管內的奇點周圍節(jié)點線性差分，并將差分結果納入到油管內的節(jié)點離散系數(shù)中去，另一個使用水管內的奇點周圍節(jié)點線性差分，并將差分結果納入到水管內的節(jié)點離散系數(shù)中去，這樣便滿足了熱流方向的物理意義。

(2)難點2：邊界條件的處理方法

盡管熱水溫度與伴熱系統(tǒng)外界的空氣溫度已知，導熱求解方程封閉，但是，稠油的真實邊界條件為稠油管道的溫度。稠油管道與系統(tǒng)內的空氣，保溫層溫度未知，這是求解稠油溫度分布不可避免的問題。解決此問題可以采用處理第三類邊界條件的邊界更新法思想，本研究將系統(tǒng)內空氣、稠油管道以及保溫層作為動態(tài)邊界條件，即將三者與稠油溫度同樣看做為非穩(wěn)態(tài)傳熱，非穩(wěn)態(tài)傳熱結束之后，將計算出的溫度場作為初場，而稠油溫度初場仍為上一管段末的溫度分布，再次進行迭代耦合求解，直到上下兩次求解結果的相對偏差符合精度要求為止，此時，系統(tǒng)內空氣、稠油管道以及保溫層的溫度場為真實的穩(wěn)態(tài)溫度場。

6 算例分析

為便于對數(shù)值計算的分析，假設熱水流量足夠大以至于整個伴熱系統(tǒng)熱水管線上，熱水溫度保持為90 ℃，稠油入口溫度為50 ℃，平均流速1 m/s，水管管徑0.4 m，管壁壁厚0.01 m，油管管徑0.6 m，管壁壁厚0.01 m，保溫層厚度0.01 m，系統(tǒng)外界空氣溫度為0 ℃。在此條件下，當投入到管道內的稠油橫截面運行1 000 s后，其整個系統(tǒng)、稠油、保溫層的溫度場分布如圖4-6所示。

圖4 伴熱系統(tǒng)溫度場Fig.4 The temperature field of heating system

圖5 稠油溫度場Fig.5 The temperature field of heavy-oil

從圖中可以看出，靠近熱水管道處的稠油溫度較高，遠離熱水管道一側的稠油溫度較低，靠近保溫層處，存在一定的溫度梯度，這符合稠油伴熱系統(tǒng)的溫度場特征；圖中顯示，保溫層中存在非常大的溫度梯度，這符合保溫層導溫系數(shù)低，保溫性能好的特點。

圖6 保溫層溫度場Fig.6 The temperature field of insulation

7 結 論

（1）本文建立了新的稠油伴熱系統(tǒng)軸向溫度場計算的物理模型與數(shù)學模型，對求解過程進行了詳細描述；

（2）對稠油熱傳導過程進行的詳細的分析與描述，并對數(shù)值模擬過程中極坐標奇點處理方法以及邊界條件處理方法進行了研究。通過對算例計算結果進行分析，證明此算法對稠油伴熱系統(tǒng)溫度場進行很好的數(shù)值模擬。

［1］ 李雪峰. 稠油集輸系統(tǒng)的熱力學分析[D]. 大慶:大慶石油學院,2007.

［2］劉文勝,郭東旭.稠油輸送技術及方法[J].石油科技論壇,2008(2):53-57.

［3］ 陶文銓. 計算傳熱學的近代進展[M]. 北京: 科學出版社, 2000.

［4］ 陶文銓. 數(shù)值傳熱學[M]. 第2版. 西安:西安交通大學出版社，2001.

［5］ Koji Fukagata. Highly energy-conservative finite difference method for the cylindrical coordinate system[J].J.Comput Phys., 2002, 181:478-498.