基于數值模擬的滑帶土蠕變特性研究

李 翔，程 聰

（中國地質大學工程學院，湖北 武漢430074）

滑坡是一種重要的地質災害，給人類的生命財產帶來重大威脅。滑帶是滑坡最重要的結構，滑坡動態演化規律的三個階段：蠕動緩滑階段、等速變形階段和加速滑動階段的內因直接與滑帶土的蠕變特性有關，而滑帶土的長期強度對滑坡的穩定性起著至關重要的控制作用。目前室內巖石三軸蠕變試驗主要用于滑坡滑帶土的蠕變特性及其長期穩定性研究，通過大量的試驗可以揭示滑坡的蠕變力學屬性，確定其參數，并建立力學模型［1—5］。但是由于室內巖石蠕變試驗費時長、耗資大，在實際操作中比較困難。而數值模擬技術的經濟性和快速性，使巖石蠕變試驗數值模擬得到了廣泛的應用［6—8］。因此，通過實驗技術及蠕變理論分析，確定滑帶土的蠕變特性，建立其蠕變模型，進而對滑坡演化趨勢進行分析，具有重要的理論意義和應用價值。

1 滑帶土的室內三軸蠕變試驗

本次三軸蠕變試驗的滑帶土取自位于黃土坡臨江Ⅱ號崩滑堆積體上TP4平硐內，滑帶土樣品的物質組成為粉質黏土夾（含）碎石（角礫），其中黏土礦物以蒙脫石、高嶺石、綠泥石、伊利石等親水礦物為主。為了研究黃土坡滑坡滑帶土長期蠕變特性，選擇了Burger’s蠕變方程，并對參數進行辨識，同時利用FLAC 3D內置的cvisc模型進行了三軸蠕變試驗數值模擬，研究了滑帶土的蠕變特性及其長期強度。

1.1 室內三軸蠕變試驗

黃土坡滑坡滑帶土的三軸蠕變試驗在中科院武漢巖土所經過改裝的三軸流變儀上進行。軸向加載采用砝碼加載，并保持原有的圍壓系統、反壓系統和孔隙水壓力系統不變，加載增量一般根據土樣的常規力學指標推算出土樣達到破壞時的應力值，并確定蠕變試驗的加載分級，一般取n＝4～8，則每級應力水平的增量為（qf/n），其中qf為在一定的圍壓σ3下的破壞應力值，加載方法采用陳氏加載法；固結壓力一般根據滑帶土的埋深來確定，垂向固結壓力σ3分別設定為200kPa、300kPa、400kPa。本次三軸固結不排水蠕變試驗的穩定標準規定為24h內變形量小于0.01mm，則可進入下一級應力水平試驗。

在黏彈性體假設的前提下，利用Boltzmann迭加原理對蠕變試驗原始數據進行處理，可以得到各級剪應力作用下的剪應變（ε）隨時間（t）變化的蠕變曲線，即分別加載蠕變曲線，詳見圖1至圖3。

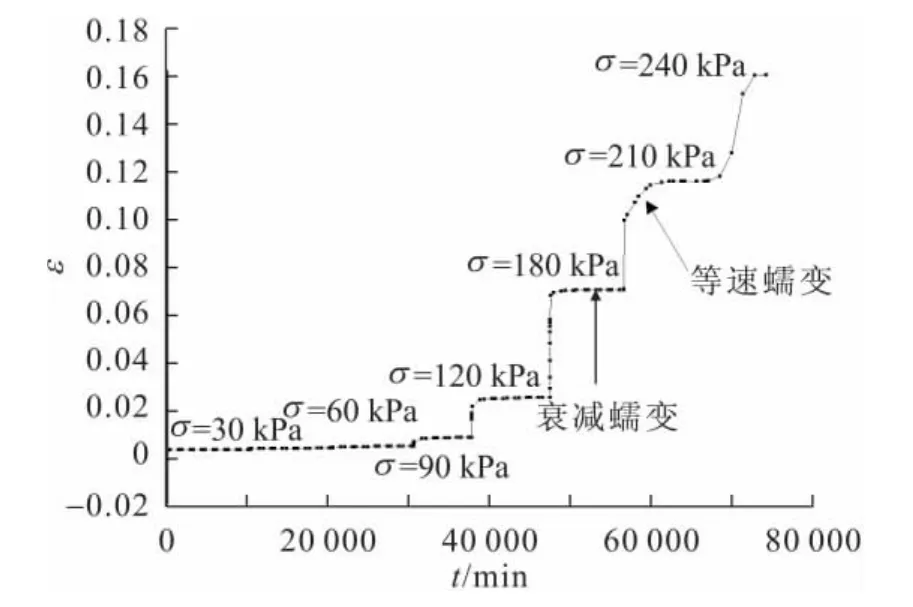
圖1 圍壓σ3為200kPa時各級剪應力下滑帶土的蠕變曲線Fig.1 Results of creep experiments under differentσ levels with 200kPaσ3

由圖1至圖3可以看出：當剪應力較小時，剪應變速率逐漸減小，最后趨向于零，試樣主要以瞬時變形為主，而沒有達到破壞，即發生衰減蠕變；隨著剪切力的增加，試樣開始出現等速蠕變階段，最后發生非衰減蠕變，試樣發生破壞。

此外，從各蠕變曲線可見，在任何一個剪切荷載作用下，試樣都存在著瞬時變形，因此可使用一個彈性元件來模擬該現象。當剪應力較低（小于長期強度）時，隨著時間的增加，剪應變速率逐漸降低，近似呈負指數的形式趨于某一漸近線，這種性質可以采用Kelvin體來模擬。將彈性元件和Kelvin體串聯起來，可以反映滑帶土蠕變變形的瞬時變形和衰減變形階段。當剪應力大于長期強度時，試樣將出現等速蠕變，并最終進入加速蠕變階段而破壞，因此在上述模型的基礎上再串聯一個黏性元件就可以模擬滑帶土的等速蠕變階段。這樣，模擬瞬時變形的彈性元件和模擬等速蠕變的黏性元件串聯，則構成了Maxwell體。

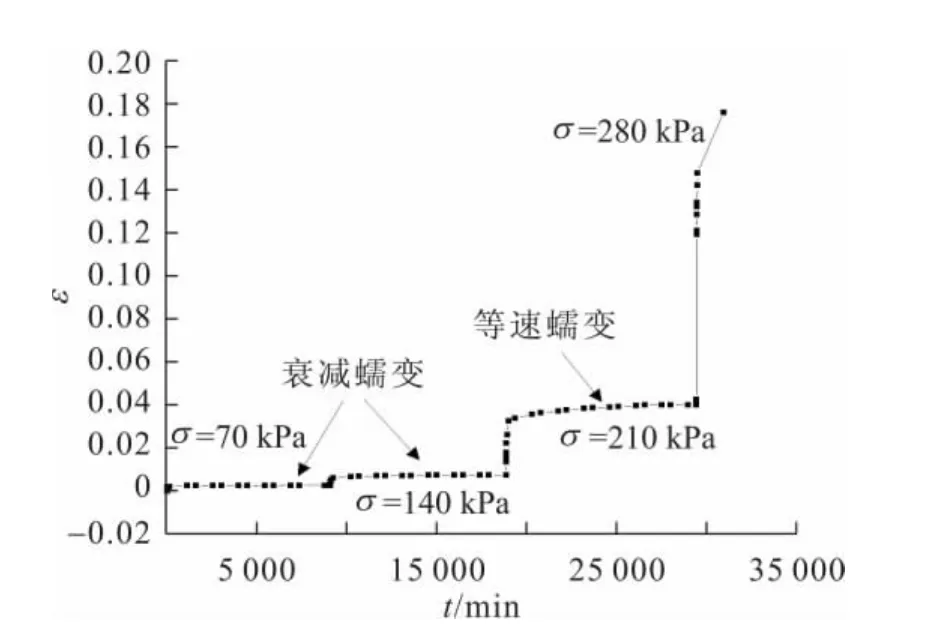
圖2 圍壓σ3為300kPa時各級剪應力下滑帶土的蠕變曲線Fig.2 Results of creep experiments under differentσ levels with 300kPaσ3

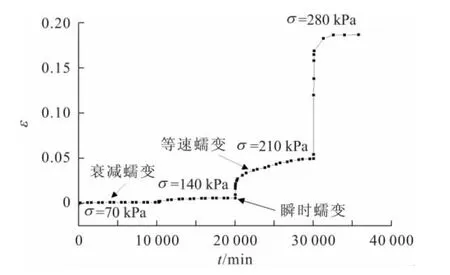
圖3 σ3為400kPa時各級剪應力下滑帶土的蠕變曲線Fig.3 Results of creep experiments under differentσ levels with 400kPaσ3

1.2 Burger’s模型及參數辨識

Burger’s模型是由Kelvin體和 Maxwell體串聯而成，如圖4所示。該模型的蠕變方程為

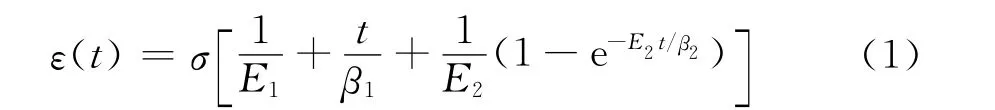
式中：ε（t）為三軸蠕變試驗過程中某級圍壓σ3及剪應力σ作用下的軸向應變；E1、E2、β1、β2分別為Maxwell和Kelvin單元的彈性模量（kPa）及黏滯系數（kPa·min）。

在剪切蠕變試驗中，對于每一個固定剪切荷載值τ，在固定的圍壓下可將式（1）改寫為如下形式：

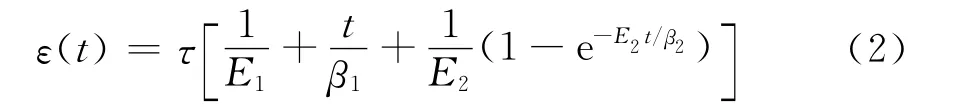
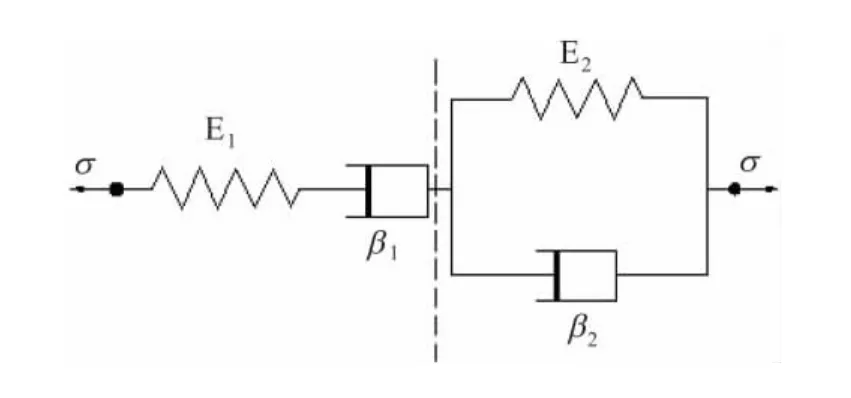
圖4 Burger’s模型Fig.4 Burger’s model

式（2）可以進一步簡化為

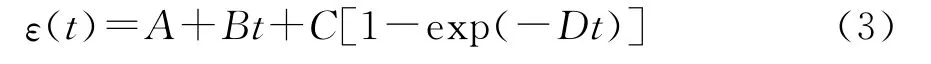
令t＝0，式（3）右端等于A，即可以根據瞬時變形來確定A；當時間足夠大時，式（3）右端最后一項趨于常數C，則式（3）可看作是直線方程，直線斜率即為B。當土體中的應力小于長期強度時將產生衰減蠕變，此時蠕變過程可能減速進行，蠕變速率逐漸減小，最后趨向于零，變形值也趨向于穩定值。由于衰減蠕變過程中沒有等速蠕變階段，因此式（3）可簡化為

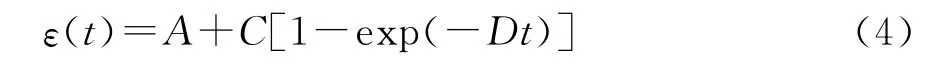
將上式中常數項移至等式左邊，在等式兩邊取對數，該式在對數坐標系中也為一直線方程，A已確定，D為直線的斜率，再將D值代入式（4）即可解出C。由此可確定一組初值，然后在 Matlab中利用lsqcurvefit非線性回歸工具可回歸出A、B、C、D的穩定解，這樣Burger’s模型所有的參數均可獲得。按上述方法，得到了各固結壓力和不同剪切力作用下的Burger’s模型的參數，詳見表1。

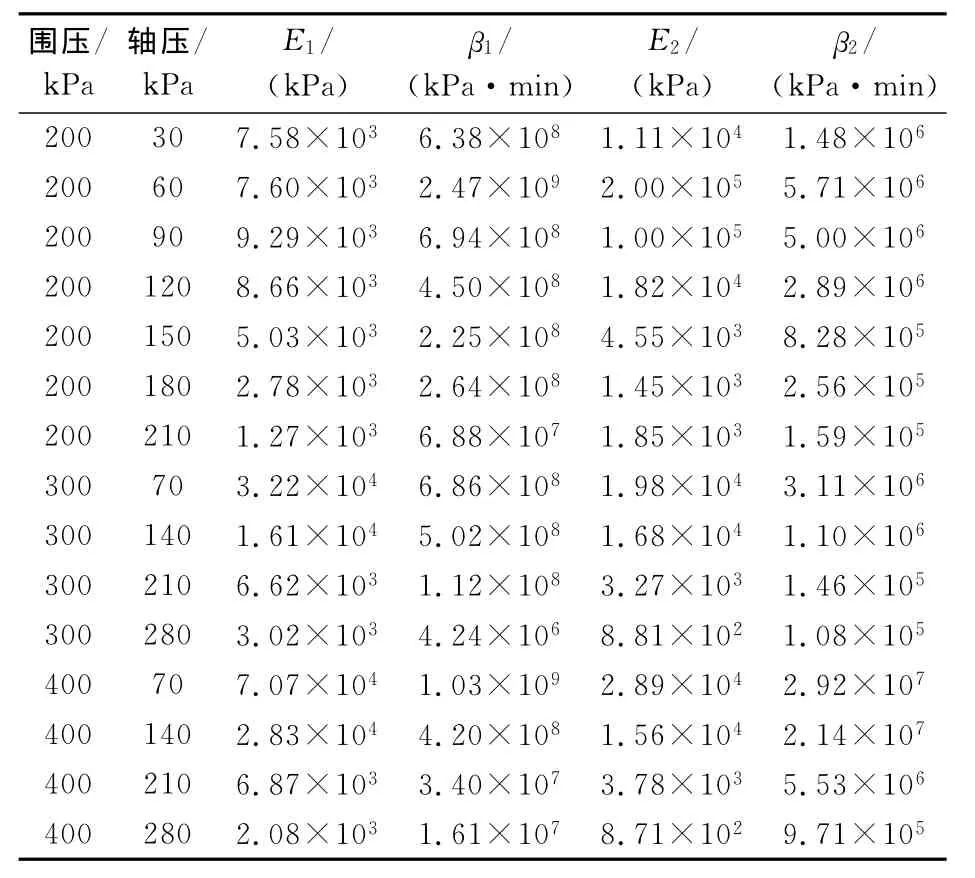
表1 Burger’s模型的參數Table 1 Parameters of Burger’s model

根據蠕變試驗數據，本文僅對圍壓為200kPa時各級剪應力下的蠕變曲線進行分析，Burger＇s模型的擬合曲線見圖5和圖6。由圖5和圖6可以看出：Burger’s模型能較好地擬合出試樣在低剪應力情況下的蠕變特性，即試樣主要以瞬時變形為主，發生衰減蠕變，隨著剪應力的增加，開始出現等速蠕變階段。

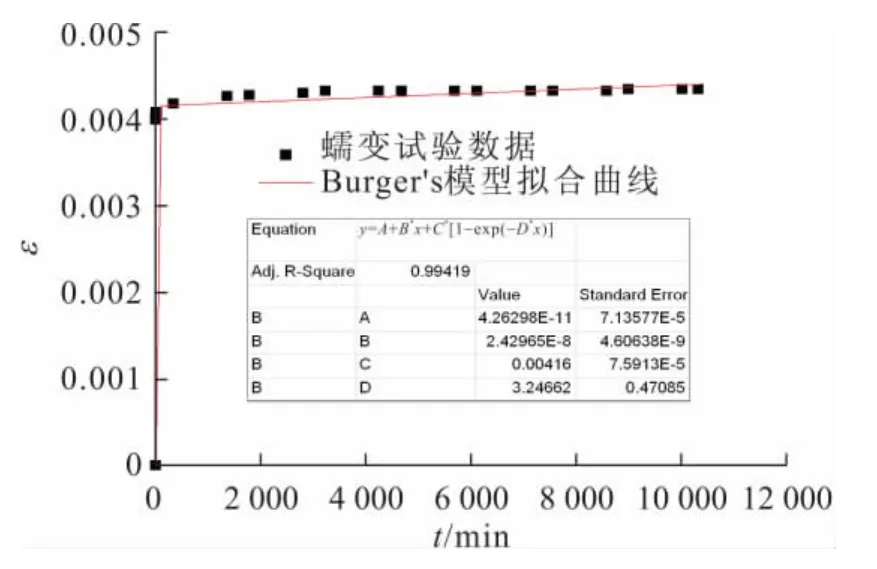
圖5 圍壓為200kPa、剪應力為30kPa時Burger’s模型的擬合曲線Fig.5 Fitting curve of Burger’s model with 200kPaσ3 and 30kPaσ

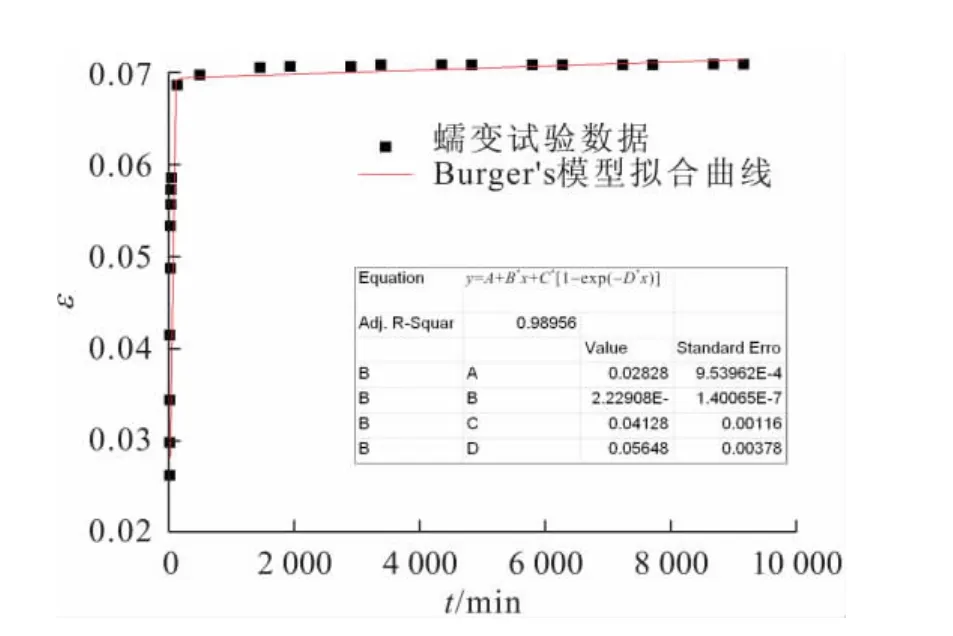
圖6 圍壓為200kPa、剪應力為180kPa時Burger’s模型的擬合曲線Fig.6 Fitting curve of Burger’s model with 200kPaσ3 and 180kPaσ

2 滑帶土室內三軸蠕變試驗的數值模擬

本文利用Burger＇s模型擬合參數并借助FLAC 3D對室內三軸蠕變試驗進行了數值模擬研究。模型的運行條件與實際的室內試驗條件相同，三軸試樣尺寸為：d＝3.91cm，h＝8cm。模型體為圓柱體，網格采取均勻劃分，劃分的網格為10×10×10，單元底面為豎向位移約束，周圍采用應力邊界條件；模型頂部荷載為分別加載，荷載為實際室內試驗的多級加載值。蠕變模型選用FLAC 3D內置的cvisc模型，即Burger’s（伯格斯）蠕變模型和摩爾－庫侖模型合成的伯格斯蠕變粘塑性模型，且采用蠕變大變形模式，根據室內三軸蠕變試驗的結果以及室內試驗時各級荷載下軸向位移量的大小，對滑帶土試樣的蠕變參數進行必要的調整后取值，并通過對室內三軸蠕變試驗進行數值模擬，可以得出不同圍壓、不同軸向應力時滑帶土分別加載的蠕變模擬曲線，見圖7至圖9。

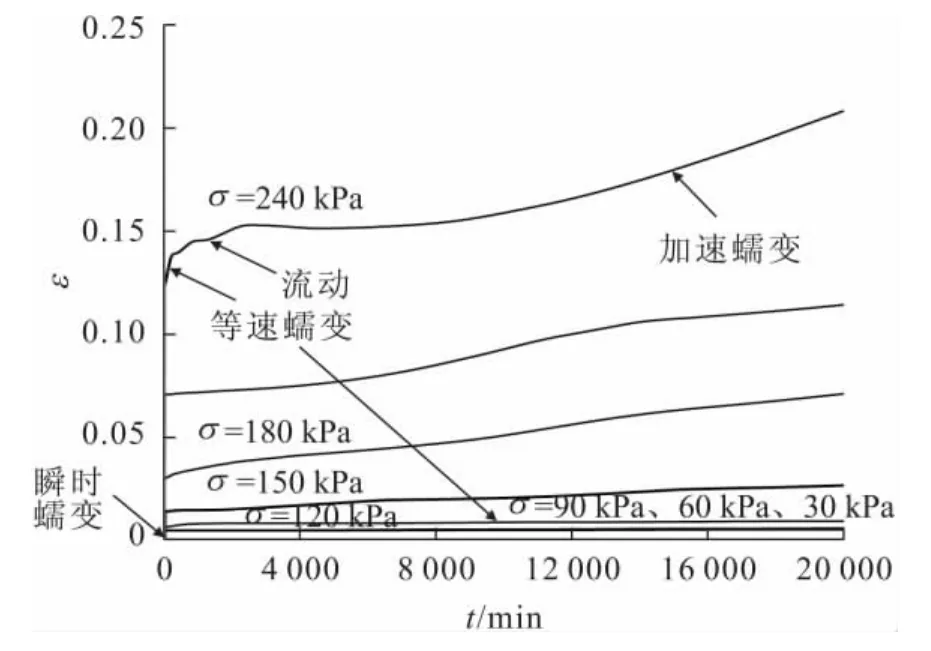
圖7 圍壓σ3為200kPa時滑帶土分別加載的蠕變模擬曲線Fig.7 Simulation curves of the creep of the slip soil under different loads with 200kPaσ3

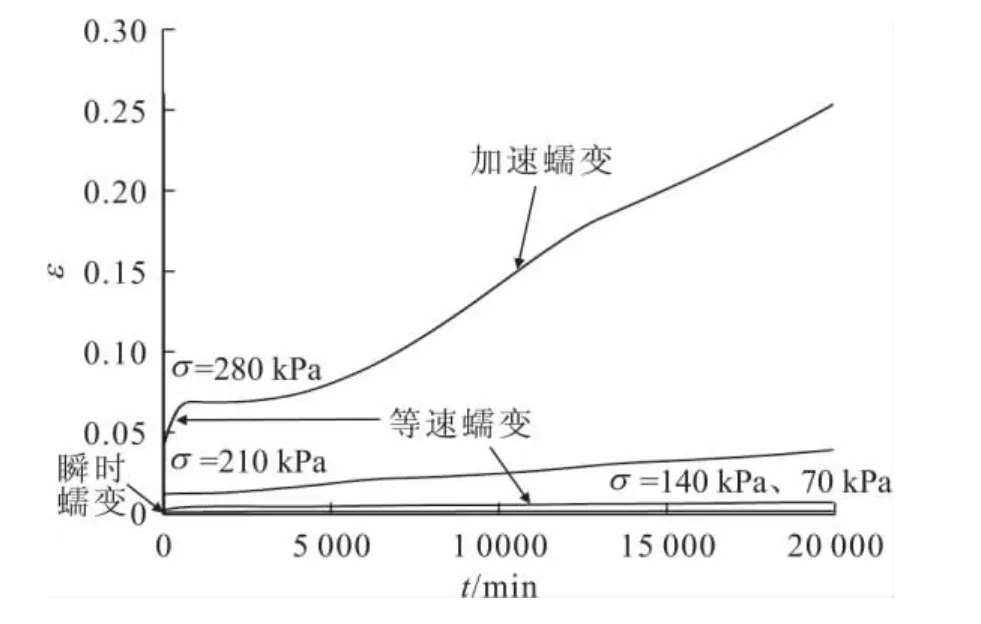
圖8 圍壓σ3為300kPa時滑帶土分別加載的蠕變模擬曲線Fig.8 Simulation curves of the creep of the slip soil under different loads with 300kPaσ3

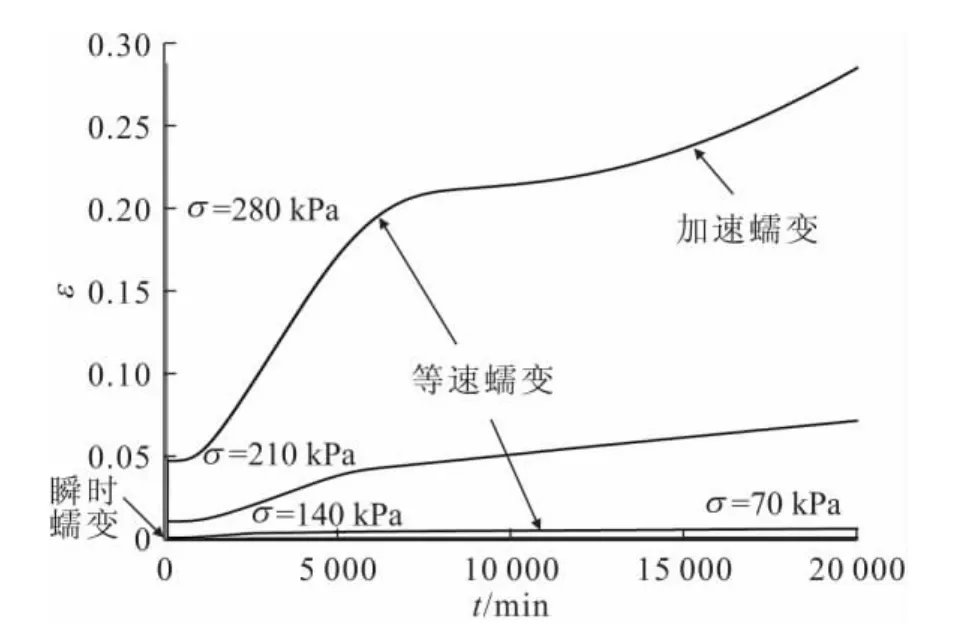
圖9 圍壓σ3為400kPa時滑帶土分別加載的蠕變模擬曲線Fig.9 Simulation curves of the creep of the slip soil under different loads with 400kPaσ3

由圖7至圖9可見，隨著圍壓的增大，滑帶土蠕變強度具有明顯的提高。較低軸向應力水平下，試件存在明顯的瞬時變形，而后產生等速蠕變；較高軸向應力水平下，試件沒有明顯的瞬時變形，而是一開始即產生等速蠕變，之后巖體的應變速率減小，隨著時間的增加，其變形趨于穩定或出現流動，直至試件發生加速蠕變破壞。

3 滑帶土的長期強度

土的非衰減蠕變的發展可引起具有加速特征的流動，并最后導致土體破壞，因此土的長期破壞強度可能小于短期荷載作用下的強度值。在實際工程中，一些線性土坡其安全系數達到或甚至超過設計要求，然而在施工完成若干年后，其強度卻降低并產生破壞，因此土的長期強度越來越引起人們的重視。在實驗室一般采用以下方法來確定土的長期強度：一種方法是將梯級加載的試驗結果在對數坐標下繪制應力－應變曲線，找到對數坐標中曲線上有明顯拐點的應力作為長期強度極限值τ∞，這是因為在非衰減蠕變階段變形值急劇增長的結果；另一種方法是根據流動速度來判斷，長期強度極限值是區別衰減蠕變和非衰減蠕變的界限值，因此可以通過繪制應力和該應力下的應變速率之間的關系曲線來判斷，曲線和應力軸的交點就是長期強度極限值τ∞。

本文采用等時曲線來確定滑帶土的長期強度，即為某時刻的應力－應變曲線。首先從數值模擬試驗中導出滑帶土分別加載蠕變曲線數據，如圖10右半部分τ1～τ6等荷載作用下的分別加載蠕變曲線；接著利用Excel，將對應于t4時間的各級應力作用下的時間－應變點A、B、C、D、E投影到圖10左半部分，并將橫坐標轉換成對應的剪應力，然后在新的坐標軸下將投影點連接起來得出其等時曲線。當試驗時間足夠長時，可以通過t∞直接獲取滑帶土的長期強度；當試驗時間較短時，也可以通過不同時刻的應力－應變曲線的拐點連線來確定長期強度。圖11至圖13為不同圍壓、不同時刻滑帶土的軸向應力－軸向應變關系曲線，即等時曲線。

由圖11至圖13可以看出：不同軸向應力下的等時曲線由近似線性段和非線性段組成，并且有轉折點，將各個轉折點連接起來，并利用指數函數進行擬合，在軸向應變達到0.15時可以認為該試樣在不同圍壓下的長期強度。采用這種方法可以得出：圍壓為200kPa下滑帶土的長期強度為130kPa，圍壓為300kPa下滑帶土的長期強度為180kPa，圍壓為400kPa下滑帶土的長期強度為200kPa。通過繪制莫爾應力圓可以得到滑帶土的長期強度參數：內聚力c∞為21.20kPa，內摩擦角φ∞為18.56°。

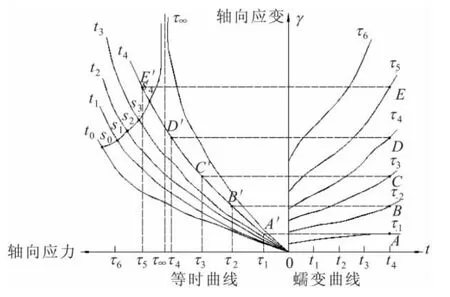
圖10 滑帶土的等時曲線圖解法示意圖Fig.10 Sketch map of isochronal curve graphical method

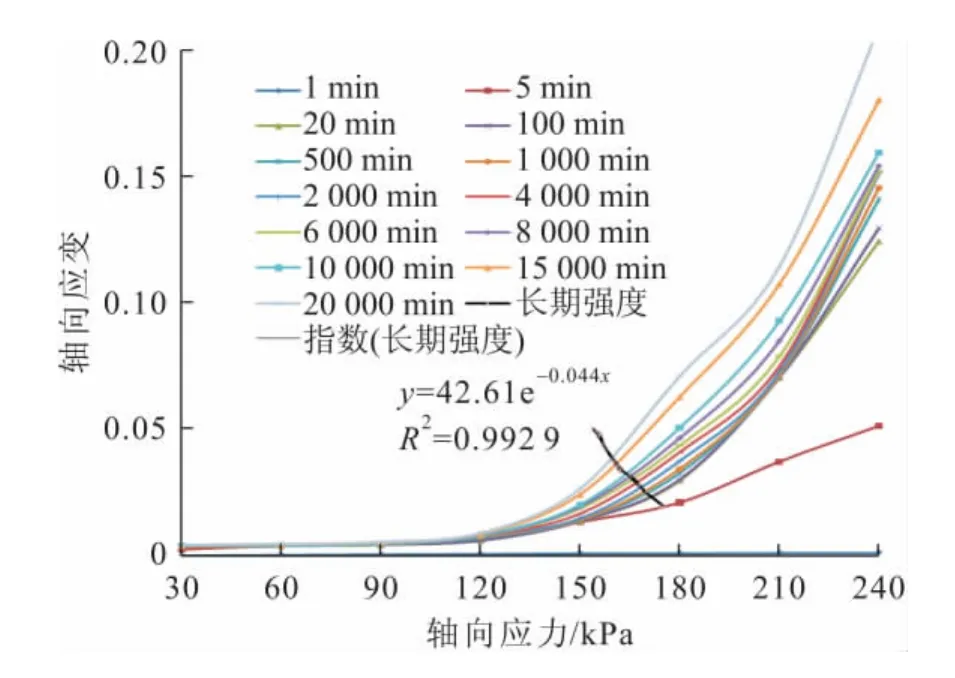
圖11 圍壓σ3為200kPa時滑帶土的等時曲線Fig.11 Isochronal curves of the slip soil with 200kPaσ3

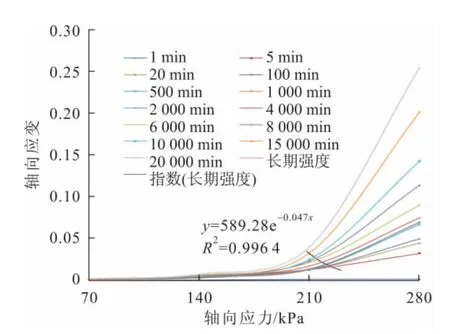
圖12 圍壓σ3為300kPa時滑帶土的等時曲線Fig.12 Isochronal curves of the slip soil with 300kPaσ3

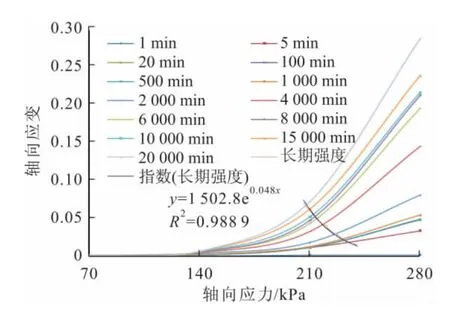
圖13 圍壓σ3為400kPa時滑帶土的等時曲線Fig.13 Isochronal curves of the slip soil with 400kPaσ3

4 結 論

（1）本文以室內三軸蠕變試驗結果為依據，通過對Burger＇s蠕變方程中各參數進行辨識，從而為描述黃土坡滑坡滑帶土的力學特性，特別是其長期蠕變特征打下了一定的基礎。

（2）數值模擬試驗結果與室內三軸蠕變試驗結果具有很好的相似性。數值模擬試驗主要依托三軸蠕變試驗結果，在滿足其誤差的基礎上，利用數值模擬，試驗結果可以獲取滑帶土分別加載下的等時曲線，從而得到滑帶土的長期強度參數：內聚力c∞為21.20kPa，內摩擦角φ∞為18.56°。

［1］汪斌，朱杰兵，唐輝明，等.黃土坡滑坡滑帶土的蠕變特性研究［J］.長江科學院院報，2008，25（1）：49－52.

［2］嚴紹軍，項偉，唐輝明.大巖淌滑坡滑帶土蠕變性質研究［J］.巖土力學，2008，29（1）：58－63.

［3］鄒良超，王世梅.古樹包滑坡滑帶土蠕變經驗模型［J］.工程地質學報，2011，19（1）：59－64.

［4］曹運江，黃潤秋.某水電站高邊坡煤系軟弱結構面流變特性試驗研究［J］.巖石力學與工程學報，2008，27（增2）：3732－3740.

［5］王琛，唐明.三峽泄灘滑坡滑動帶土的Singh－Mitchell蠕變方程［J］.四川大學學報（工程科學版），2003，35（5）：93－95.

［6］王旭東，付小敏.壓縮蠕變力學試驗的數值模擬研究［J］.工程地質學報，2009，17（4）：533－537.

［7］鄭俊.某滑坡滑帶土流變模型構建及FLAC3D二次開發［D］.宜昌：三峽大學，2009.

［8］陳育民，劉漢龍，鄧肯·張.本構模型在FLAC3D中的開發與實現［J］.巖土力學，2007，28（10）：2123－2126.

［9］Itasca Consulting Group.FastLagrangianAnalysisofContinua in3Dimensions［M］.MN.USA：Itasca Consulting Group Inc.，Minneapolis，2002.

［10］周德培等.流變力學原理及其在巖土工程中的應用［M］.成都：西南交通大學出版社，1995.