基于方差分析的經管類專業學生必備數學知識重要性的調查研究
何靜,方建衛
(重慶人文科學技術學院,重慶401524)
基于方差分析的經管類專業學生必備數學知識重要性的調查研究
何靜,方建衛
(重慶人文科學技術學院,重慶401524)
本文對經管類三個專業學生進行了必備數學知識重要性的調查,并分析數據得出了一些有意義的結論,對經濟數學的教學工作具有一定的指導性作用。
總觀測變異;F分布;方差分析
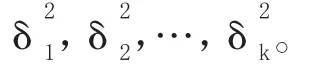
于是可建立原假設:H0:μ1=μ2=…=μk;H1:μ1,μ2,…,μk不全相等。為對H0進行檢驗,通常對樣本數據的總觀測變異(SST)進行分解:一部分為組內均值變異(SSW),它是每個觀察數據與其所在組平均值離差的平方和,它反映了數據xij抽樣誤差的大小,是隨機誤差,又稱為誤差平方和。另一部分為組間均值變異(SSB),它是各組平均值與總平均值離差的平方和,它反映了各總體的樣本平均值μi之間的差異程度,在一定程度上反映了各總體均值之間的差異,可反映由因素影響所導致的系統誤差。若SSB顯著大于SSW,則說明各組平均值之間的差異顯著大于抽樣誤差,表明各組平均值之間的差異并不僅僅是由于隨機波動引起的,是有系統波動的,從而原假設不能成立。這種通過比較方差大小來推斷原假設是否成立的方法稱為方差分析法。
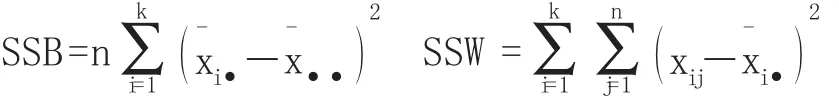
故若F的觀察值大于其臨界值,則拒絕原假設H0;反之接受原假設H0。對概率P的觀察值,若小于規定的顯著性水平α,則拒絕原假設,否則接受原假設。可將其總結于一張表內,其形式如下:

如果H0成立,則表明自變量和因變量之間沒有關系,自變量對因變量的影響不顯著。若H0不成立,則說明自變量對因變量的變動有顯著的影響,即自變量不同分組的因變量均值是顯著不同的。
據此用單因素方差分析法來進行必備數學知識重要性的調查研究。
在實際的教學工作中,經常會出現經管類學生對必備數學知識學習接受程度的差異性問題。為了根據實際需要合理設計各專業經濟數學的教學內容,達到因材施教的目的,調查了金融、會計、工程管理三個專業共計300個受訪者。為簡便期間在各組中隨機抽取了6個人,測量了他們對于必備數學知識的重要性認識。用十級量表,最高為10分,最低為0分,數據見下表,計算數據有四舍五入誤差。
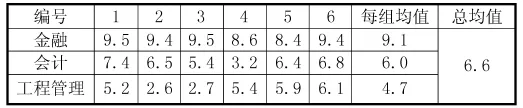
建立原假設:不同的專業對必備數學知識的重要性認識程度一樣。用統計語言表示為:H0:μ1=μ2=μ3。分別計算總變異SST,組間均值變異SSB和組內均值變異SSW。
其中:SST=(9.5-6.6)2+(9.4-6.6)2…+(6.1-6.6)2=88.8
SSB=6×(9.1-6.6)2+6×(6.0-6.6)2+6×(4.7-6.6)2≈63.8
SSW=(9.5-9.1)2+…+(7.4-6.0)2+…+(5.2-4.7)2+…+(6.1-7.7)2=25
于是有下列方差分析表:
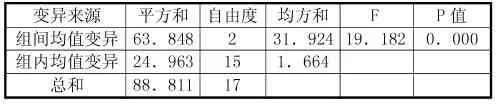
因為F=SSB/(K-1)/[SSW/(N-K)]=19.2,查F分布表可知,F(2,15)=6.51,顯然計算出的F值遠遠大于臨界值,于是拒絕原假設。即不同的專業對必備數學知識的重要性認識程度是不一樣的。
在應用單因素方差分析時,應注意:方差分析是假定各觀測數據是從具有相同方差且相互獨立的總體中抽取的。對于不同的誤差項,它們之間是不相關的。若誤差項之間是相關的,那么F值會被扭曲,嚴重影響到結果的客觀性。上述經管類學生對必備數學知識學習接受程度的差異性問題所選取的樣本是同一個學院學習同一門經濟數學課程的不同專業的學生,樣本個體之間是相互獨立的,符合應用單因素方差分析的前提。
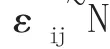
因子的第i種效應αi是指除了因子對試驗指標的平均影響之外,因素的第i種水平對試驗指標的特殊影響。上面通過方差分析得出了不同因素水平對試驗指標的影響是顯著不同的,但卻未給出何種因素水平的效應最大,因而還有必要進一步分析。對于上面的數學模型來說,除了進行各總體均值的差異外,還能求出各水平效應αi的點估計和區間估計。
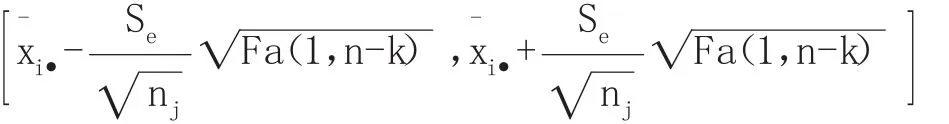
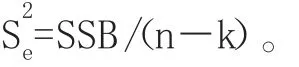
下面還是對上述經管類學生對必備數學知識學習接受程度的差異性問題進一步分析。金融專業的抽樣調查數據可認為是第一個因素水平,會計專業的抽樣調查數據可認為是第二個因素水平,工程管理專業的抽樣調查數據可認為是第三個因素水平。
為此,根據不同因素水平效益的點估計公式,有:
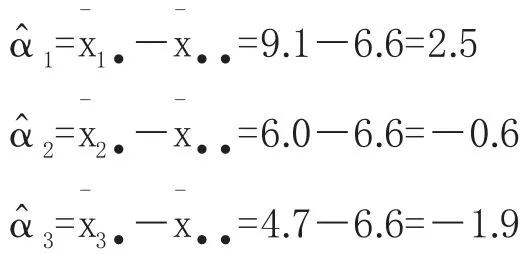
由此得出結論,對于經管類不同專業的學生而言,必備數學知識在后續專業的學習過程中的作用是不徑相同的。雖然教學課程都是經濟數學,但是根據不同專業的需要教師在課堂教學過程中應合理的安排教學內容和教學程度,以達到更好的教學效果的目的。
[1]盛驟,謝式千,潘承毅.概率論與數理統計[M].北京:高等教育出版社,2005.
[2]馮梅.教師對教學質量影響程度的單因素方差分析[J].數學的實踐與認識,2005,(11).
[3]田兵.單因素方差分析的數學模型及其應用[J].陰山學刊,2013,(6).
G 642.0文獻標志碼:A文章編號:1674-9324(2014)50-0198-02
【教師觀點】

