扇圖與輪圖的［r，s，t］－著色

張新軍

（莆田學院 數學學院，福建 莆田 351100）

0 引 言

圖的著色理論是圖論中一個非常重要的分支，有廣泛的應用，如排課表問題、存儲問題、電路安排問題、交通問題、頻道分配問題等。作為一般點著色、邊著色和全著色的推廣，2007年，A.Kemnitz和 M.Marangio［1－2］提出了圖的［r，s，t］－著色和［r，s，t］－色數的定義，給出有關的一些性質、定理，并討論完全圖的［r，s，t］－色數。在文獻［3－4］中討論了二部圖和樹路的［r，s，t］－色數，在文獻［5－7］中分別討論圈和星圖的［r，s，t］－色數，文獻［8］給出了超圖的［r，s，t］－著色和［r，s，t］－色數。文中主要討論了扇圖和輪圖的［r，s，t］－色數。

1 預備知識

文中所涉及的圖G均為簡單有限連通圖，Δ（G）＝Δ表示圖G（V，E）的最大度，VΔ表示由最大度頂點的集合，χ（G），χ′（G），χ″（G）和χr，s，t（G）分別表示點色數、邊色數、全色數和［r，s，t］－色數，未定義的符號和術語可參見文獻［9］。

下面給出［r，s，t］－著色和［r，s，t］－色數的定義：

定義1［1］給定非負整數的r，s和t，且max｛r，s，t｝≥1，圖G（V，E）的一個k－［r，s，t］－著色是指從V（G）∪E（G）到｛0，1，…，k－1｝，k∈N的一個映射c，如果c滿足下列條件：

1）對V 中相鄰的點vi，vj，有｜c（vi）－c（vj）｜≥r；

2）對E中相鄰的點ei，ej，有｜c（ei）－c（ej）｜≥s；

3）對V∪E中相關聯的點vi和邊ej，有｜c（vi）－c（ej）｜≥t。

則稱c為G 的一個［r，s，t］－著色。

定義2［1］使得圖G 存在［r，s，t］－著色的最小的 值k，稱 為 圖 G 的 ［r，s，t］－色 數，記 作χr，s，t（G）。

顯然，［r，s，t］－著色是對點著色、邊著色和全著色的推廣，因為［1，0，0］－著色是正常的點著色，［0，1，0］－著色是正常的邊著色，［1，1，1］－著色是正常的全著色，即

下面幾個引理是文獻［1］得到的部分結論。

引理1［1］若 H?G，則χr，s，t（H）≤χr，s，t（G）。

引理2［1］若r′≤r，s′≤s，t′≤t，則

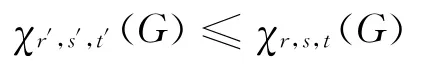
引理3［1］

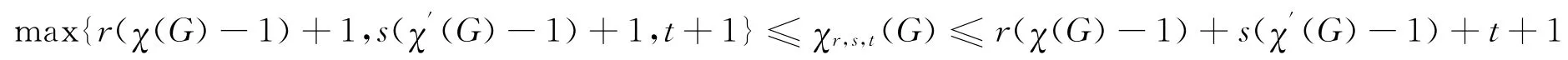
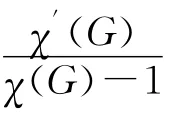
2 主要結果及證明

定義3 扇圖Fn＝Pn－1＋O1，其中Pn－1為n－1階的路，O1為一個孤立點。

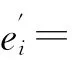
定理1 若G＝Fn（n≥4），則

1）

2）

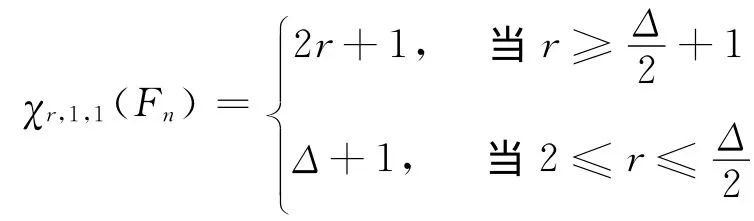
3）當s≥2時，χ1，s，1（Fn）＝（Δ－1）s＋1。

4）χ1，1，t（Fn）＝Δ＋t＋1。

證明：

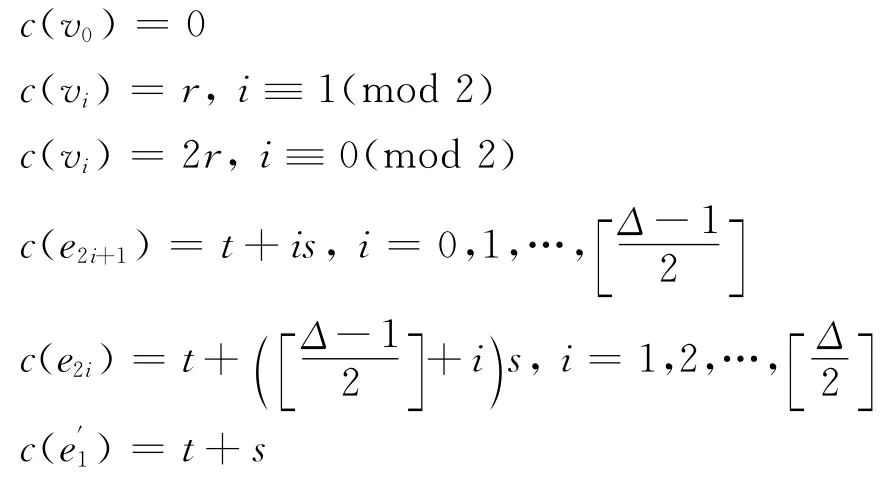
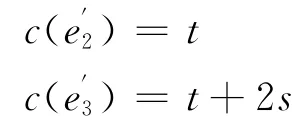
其余的邊可用t和t＋s交替著色。所以

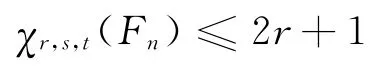
又

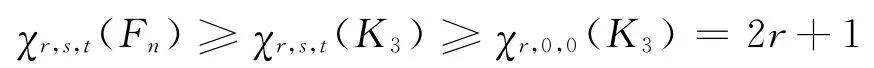
故

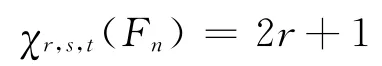
當（Δ－1）s≥2r＋2t且s≥2t，r≥2s時，有（Δ－1）s－（2r＋t）≥t，s－t≥t且r＋t－2s≥t，于是可對Fn進行如下的［r，s，t］－著色：

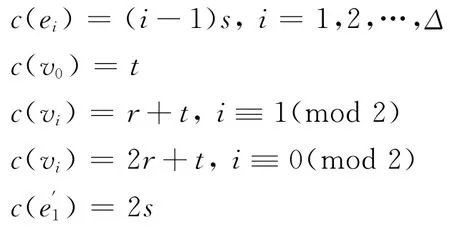
其余的邊可用0和s交替著色。所以

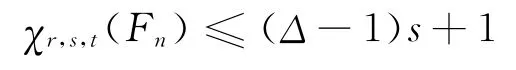
又

所以

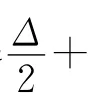
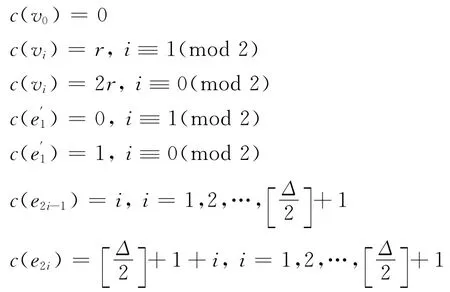
然后進行檢驗，如果發現有兩條邊和它對應的端點的顏色相同，則可以互換這兩條邊的顏色；若只有一條邊的顏色和端點的顏色相同，則可將這條邊的顏色和著2r的這個頂點所對應的邊的顏色互換。這樣總共用Δ＋1種顏色，即χr，1，1（Fn）≤Δ＋1，又由引理2知

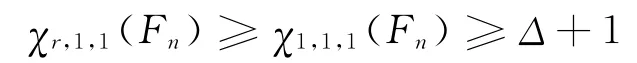
所以

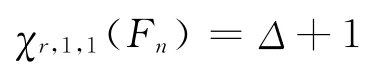
3）由引理 2 知，χ1，s，1（Fn）≥χ0，s，0（Fn）＝（Δ－1）s＋1。當n＝4時，因為s≥2，所以2s－1≠s，2s≠2，可進行如下著色：

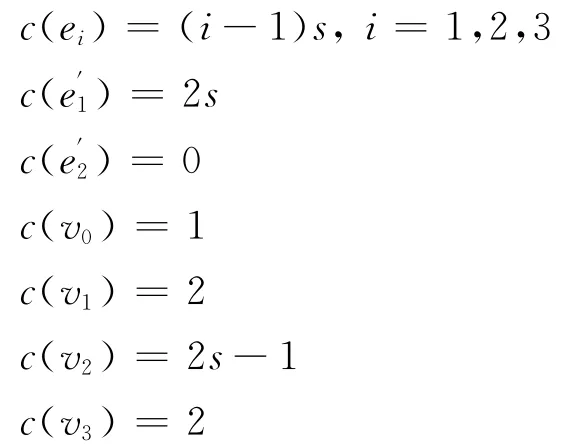
所以

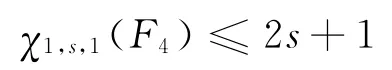
因此

當n≥5時，因為s≥2，所以2s－1≠s，3s－1≠2s，于是可進行如下著色，如圖1所示。

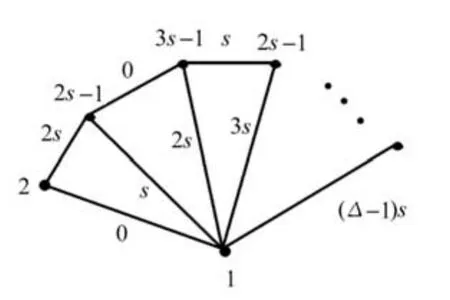
圖1 當n≥5，s≥2時扇圖的［1，s，1］－著色

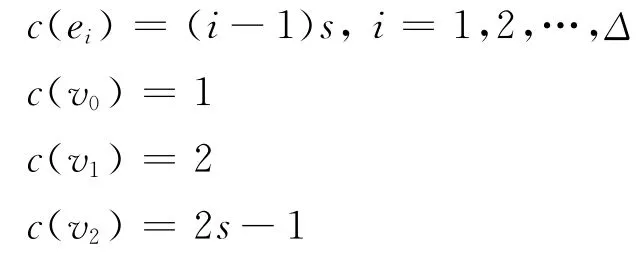
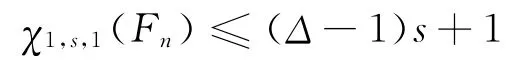
所以

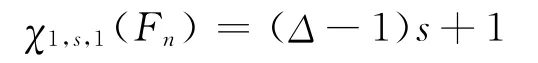
4）因為G＝Fn且n≥4，所以

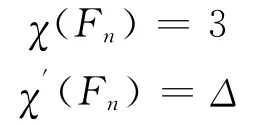
由引理3知

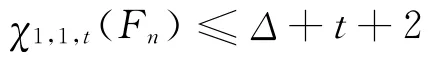
當n＝4時，因為r＝s＝1，t≥1，所以可進行如下著色：

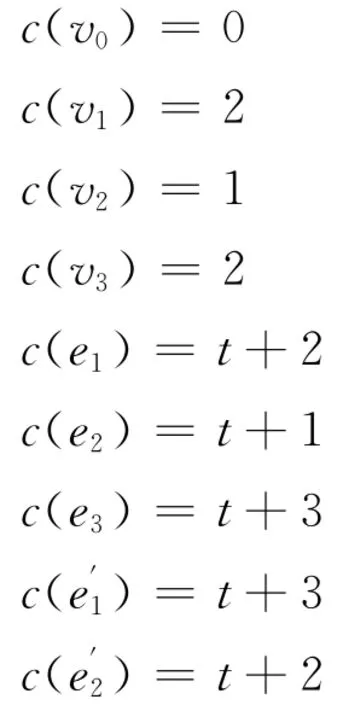
共需t＋4＝Δ＋t＋1種顏色。于是

考慮K1，3：對K1，3來說，因為Δ＝3，所以如果要對其進行［1，1，t］－著色，則需要t＋4種顏色。而由引理1知

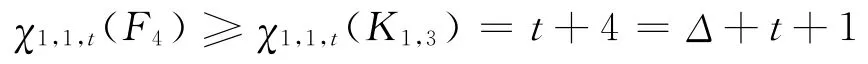
所以

當n≥5時，可進行如下著色：

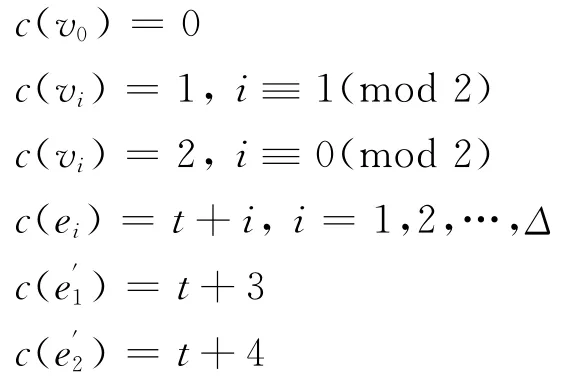
其余的邊可用t＋2和t＋3進行交替著色。這樣就得到一個［1，1，t］－著色。即

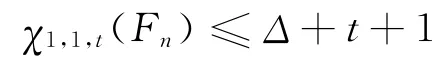
由引理1知

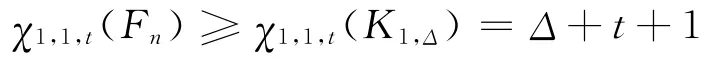
所以

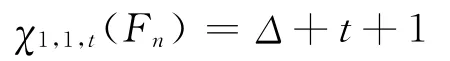
綜上所述，χ1，1，t（Fn）＝Δ＋t＋1。

下面研究輪圖的［r，s，t］－色數。

定義4 輪圖Wn＝Cn－1＋O1，其中Cn－1表示長度為n－1的圈。

當n≥7為奇數時，有如下定理成立。

定理2 設G＝Wn（n為奇數，n≥7），則

1）

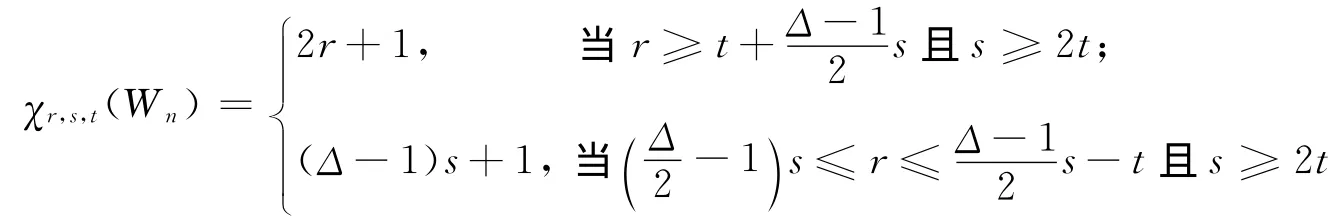
2）

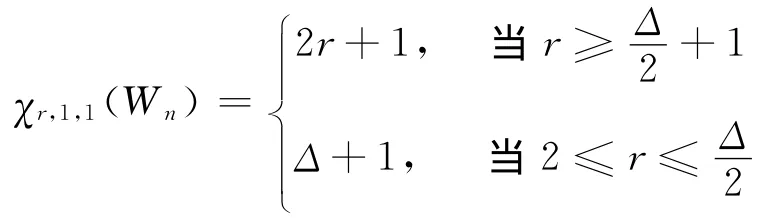
3）當s≥2時，χ1，s，1（Wn）＝（Δ－1）s＋1。

4）

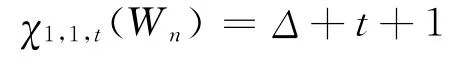
證明

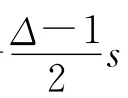
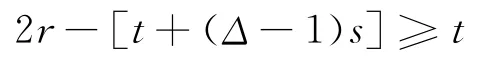
且

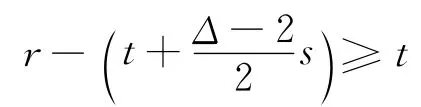
于是可以進行如下著色（當n＝9時）如圖2所示。

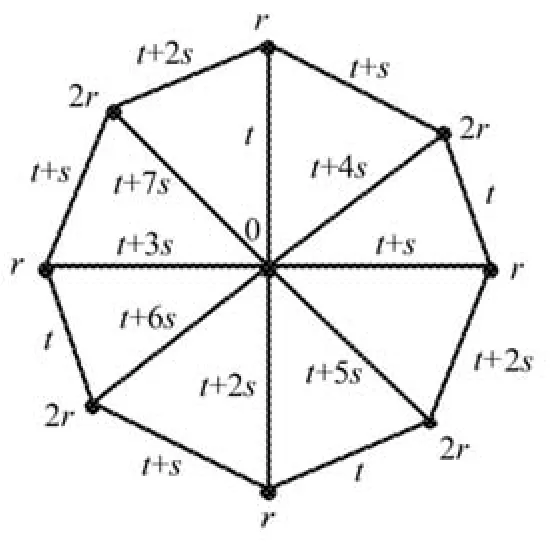
圖2 當n＝9時輪圖的［r，s，t］－著色

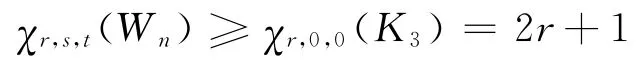
又所以

χr，s，t（Wn）＝2r＋1

因為

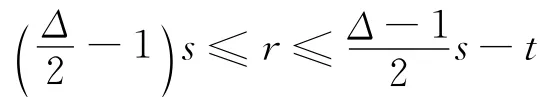
且s≥2t，所以

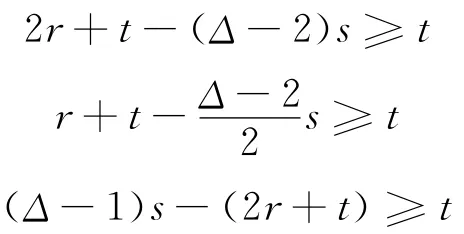
所以可以進行如下著色：

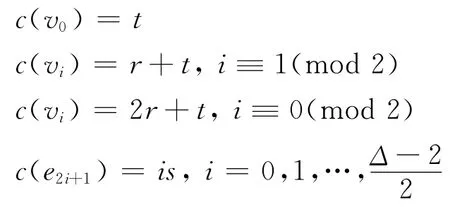
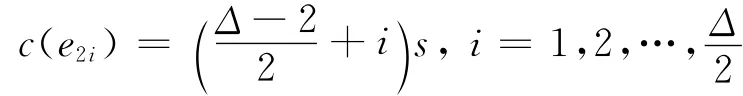
另一方面

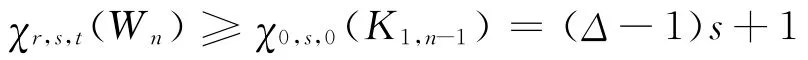
所以

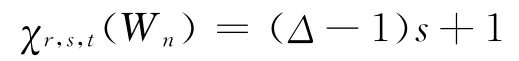
2）因為G＝Wn（n為奇數，n≥7），所以

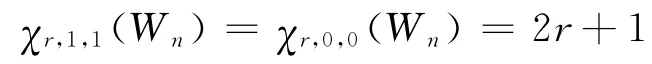
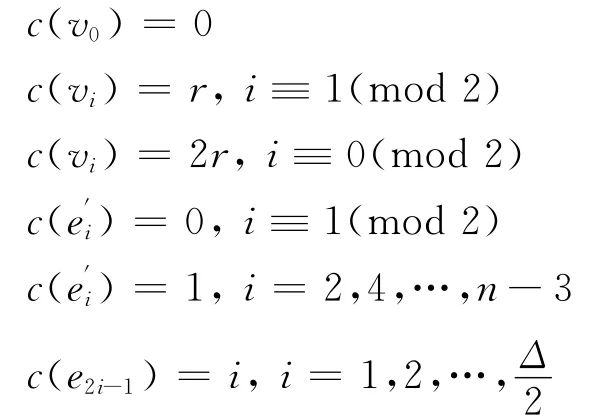
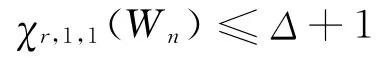
由引理2知

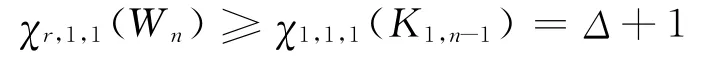
所以

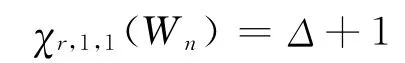
當n≥6為偶數時，有如下定理成立。

定理3 設G＝Wn（n為偶數，n≥6），則

1）

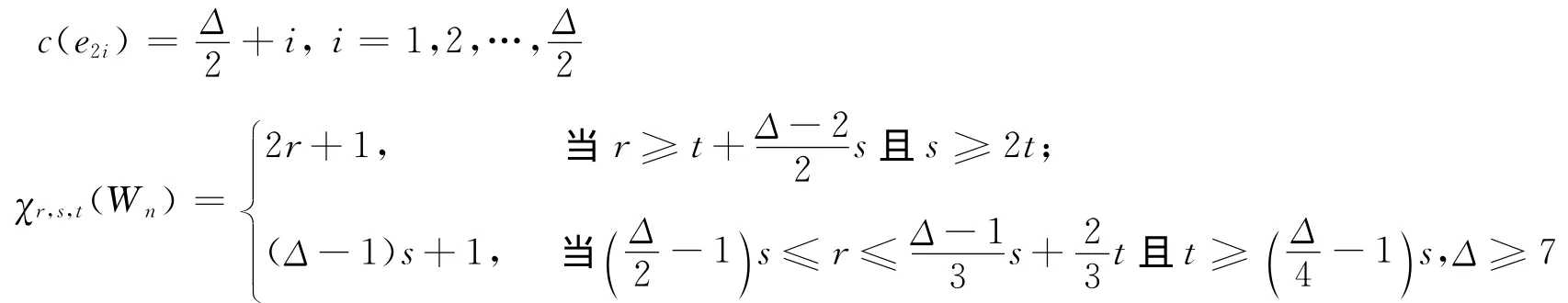
2）

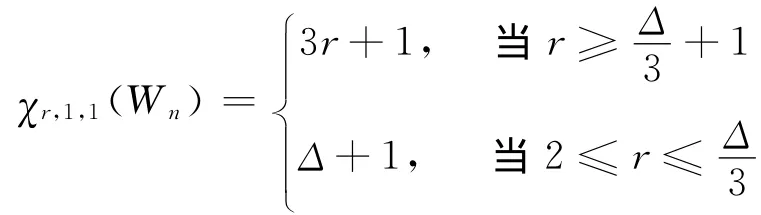
3）當s≥2時，χ1，s，1（Wn）＝（Δ－1）s＋1。

4）

證明

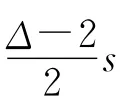
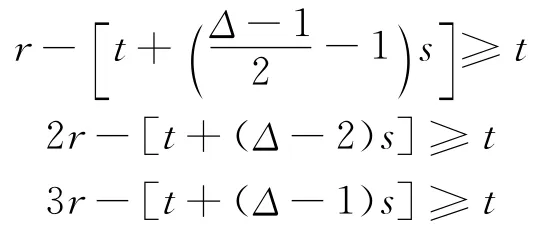
于是可以進行如下著色：

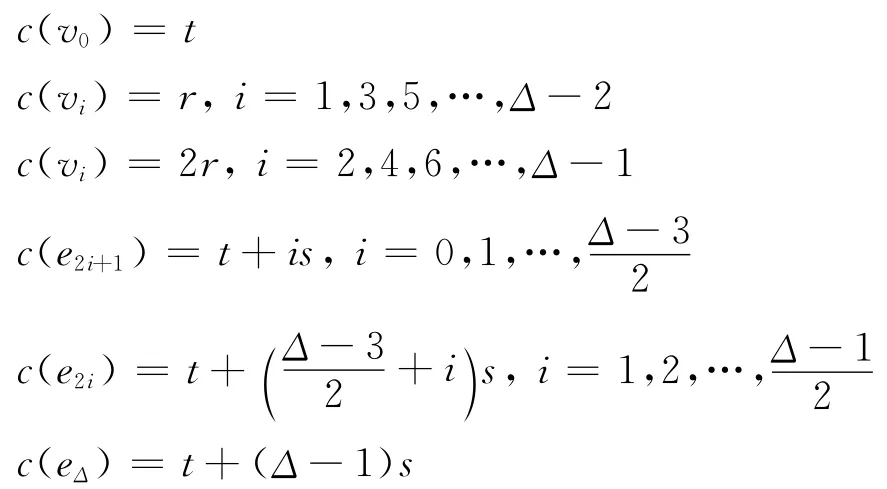
其余的邊可用t，t＋s和t＋2s這3種顏色進行著色，所以

又由引理2知

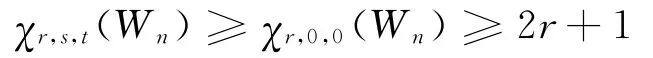
所以

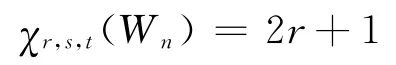
因為

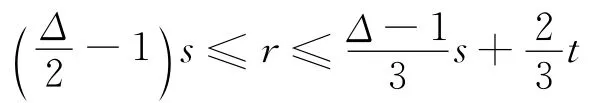
且

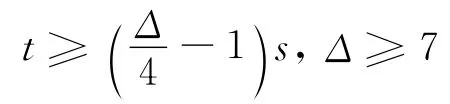
所以

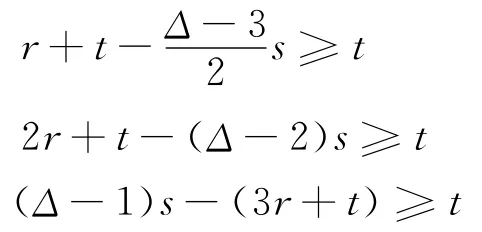
于是可以作如下著色，如圖3所示。

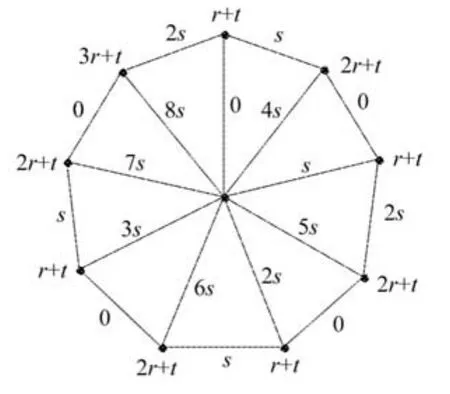
圖3 當n＝10時輪圖的［r，s，t］－著色

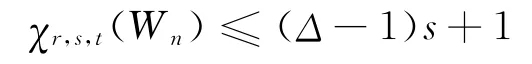
又因為

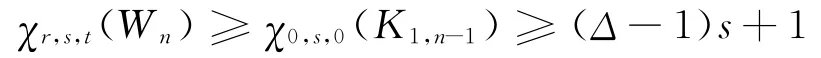
所以

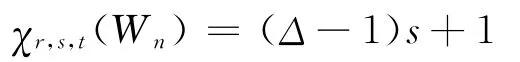
2）因為n（n≥6）為偶數，所以

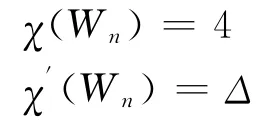
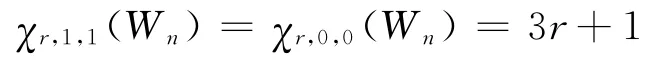
然后檢驗輪輻，如果只有一條邊的顏色和端點的顏色相同，則可將這條邊的顏色和著2r的這個頂點所對應的邊的顏色互換，如果有兩條邊和它對應的端點的顏色相同，則可以互換這兩條邊的顏色；如果有3條邊和它對應的端點的顏色相同，則可以輪換這3條邊的顏色，使這3條邊和它們對應的端點的顏色不同；最后，對e′n－1這條邊可以用｛0，1，…，Δ｝／｛0，1，c（eΔ），r，2r｝（c（eΔ）表示邊eΔ所用的顏色）中的一種顏色進行著色，這樣總共用Δ＋1種顏色。即

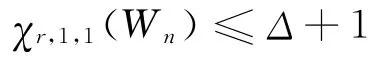
又由引理2可得

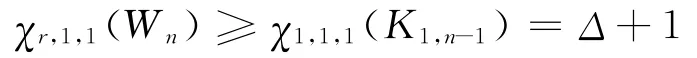
所以

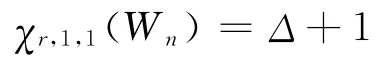
3）由引理2知

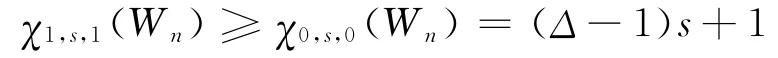
因為n≥6且s≥2，所以2s－1≠s，3s－1≠2s，于是可進行如下著色：

所以

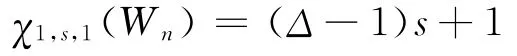
4）因為n≥6，所以Δ≥5，于是可進行如下著色：

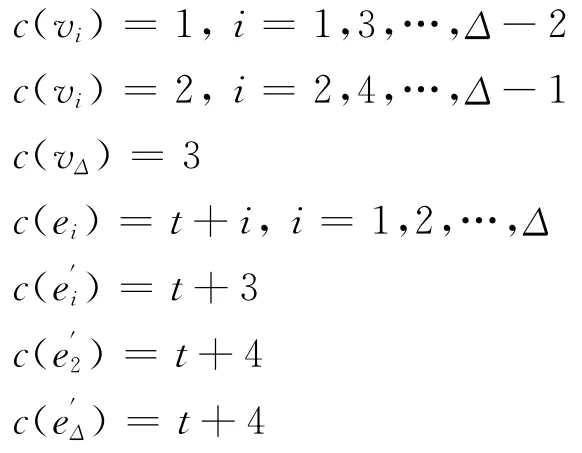
其余的邊可用t＋2和t＋3進行交替著色。這樣就得到一個［1，1，t］－著色。即

而由引理1知

所以

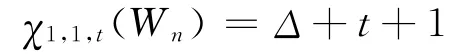
對圖的［r，s，t］－著色還有很多值得完善的地方，很多圖的［r，s，t］－色數都還沒精確的結果，這也是后續要完成的重要的工作。

［1］A Kemnitz，M Marangio.［r，s，t］－colorings of graphs［J］.Discrete Math.，2007，307：199－207.

［2］A Kemnitz，M Marangio.［r，s，t］－chromatic numbers and hereditary properties of graphs［J］.Discrete Math.，2007，307：916－922.

［3］龔劬，張新軍.二部圖的［r，s，t］－著色［J］.重慶大學學報：自然科學版，2007，30（12）：95－97.

［4］L Dekar，B Effantin，H Kheddouci.［r，s，t］－coloring of trees and bipanrtite graphs［J］.Discrete Mathematics，2010，310（2）：260－269.

［5］A Kemnitz，J Lehmann.［r，s，t］－colorings of stars［J］.Congressus Numerantium，2007，185：65－80.

［6］M S Villà.［r，s，t］－colorings of paths，cycles and stars［J］.Doctoral Thesis，TU Bergakademie，Freiberg，2005：665－689.

［7］Changqing Xu，Xianli Ma，Shouliang Hua.［r，s，t］－Coloring of kn／n［J］.J.Appl.Math.Comput，2009，31：45－50.

［8］張新軍.超圖的［r，s，t］－著色［J］.莆田學院學報，2012，19（2）：7－10.

［9］J A Bondy，U S R Murty.Graph Theory［M］.Berlin：Springer，2008.