基于直角坐標的電力系統潮流計算方法研究

(廣西電網公司崇左供電局，廣西 崇左 532200)

1 引言

潮流計算是電力系統運行與規劃的重要手段，也是電力系統安全穩定分析的基礎。其主要目標是在給定的運行方式下求電力系統節點的電壓以及輸電線路的功率[1]。電力系統是非線性系統，潮流方程的求解實質上是求解非線性的方程組。早在1950年初,潮流計算就開始采用高斯-塞德爾法，該方法以節點導納矩陣為基礎,其優點是計算過程簡便且對計算機的要求不高,易于編程實現，在早期得到了一定的發展應用。但是高斯-塞德爾法并不是多項式時間算法，其收斂性差,在求解變量較多是其計算量急劇增加，甚至不收斂。為改善收斂性問題，60年代初以阻抗矩陣為基礎的阻抗法開始出現，該方法改善了收斂性，但是阻抗陣是滿矩陣，計算量大且需要很大的內存空間。1960年后，牛拉法和P-Q分解法相繼出現，這些算法不但收斂性好，且對計算機的要求也大大降低。

由于我國電源分布與負荷分布不平衡，就南方電網而言，水電等大量清潔能源主要分布于西部地區云南、貴州等，而負荷中心則分布在廣東，高壓直流輸電的出現，使原有的潮流計算方法已不再適用，必須對其加以改進。文獻[2-3]詳細分析了含直流輸電線路的交直流潮流交替求解算法的流程，論述交流系統和直流系統之間的相互影響特性。直流輸電電能轉換裝置有不同的控制方式[4]，文獻[5]采用計算機進行控制方式轉換的方法,計算效果較好。風電等新能源的出現也對傳統的潮流計算方法提出了挑戰。風電存在不確定性、間歇性等因素，其接入電網后電源也存在不確定性，傳統的潮流計算模型則以確定性的電源功率為基礎。聯合迭代算法在計算含風電的電力系統潮流時有較好的效果[6-8]，其通過修正雅克比矩陣解決了計算精度與迭代次數之間的矛盾。

2 牛頓法求解電力系統潮流

牛頓法是把非線性的方程式簡化為線性方程式，通過求解線性方程來得到原方程的近似解。線性化的過程如下：

設有非線性方程

f(x)=0

(1)

設x(0)為該方程式的初值，則精確解x可表示為：

x=x(0)-Δx(0)

(2)

f(x(0)-Δx(0))=0

(3)

按泰勒級數展開：

(4)

選擇的初值接近精確解時，Δx(0)很小，(Δx(0))2和更高次項可忽略不計，因此可化為：

f(x(0))-f′(x(0))Δx(0)=0

(5)

這個方程稱為修正方程式，可以求出修正量Δx(0)。由于Δx(0)是由簡化公式求得，所以此時x=x(0)-Δx(0)不是精確解。可令：

x(1)=x(0)-Δx(0)

(6)

將x(1)代入公式(5)，得：

f(x(1))-f′(x(1))Δx(1)=0

(7)

這樣可以得到更加接近精確解的x(2)：

x(2)=x(1)-Δx(1)

(8)

如此不斷反復下次，就可以得到符合要求的近似解。

3 常數雅克比矩陣潮流計算

潮流計算一般以節點功率和電壓表征電力系統的運行特性，電力系統節點的功率方程為：

(9)

其中Pi、Qi分別為節點i的有功功率和無功功率，Vi、Vj分別為節點i、j的電壓，j∈i表示節點j與節點i相連，Yij為線路導納。本文在推導的過程中用直角坐標形式表示節點電壓Vi和導納Yij，即

(10)

將式(10)代入式(9)，則得到復數形式表示的節點功率方程式(11)，此時變量由傳統潮流計算的變量電壓幅值和相角V、θ轉換為電壓的實部和虛部e、f。

(11)

將式(11)進一步展開，就可以得到節點的有功功率和無功功率表達式(12)，即基于直角坐標的節點功率方程。

(12)

考慮潮流計算中節點的發電機出力以及節點的負荷后，電力系統潮流計算方程式可以寫為式(13)。

(13)

其中PGi、PLi分別為節點i的電源有功功率和有功負荷，QGi、QLi分別為節點i的電源無功功率和無功負荷，包括無功補償器補償的無功功率。該潮流計算模型中沒有正余弦函數，在求解的過程中相對簡便，且節約計算時間和計算機的容量。對方程式(13)的求解，用求增量形式Δe、Δf的方法，即如式(14)。

(14)

其中e0、f0為節點電壓實部和虛部的初值，將式(14)展開后就可以得到只含e0、f0和只含Δe、Δf的兩部分，并令：

(15)

取平啟動的初值e0=1、f0=1并將式(15)代入式(14)，得到最終的潮流計算方程式(16)。

(16)

將式(16)寫成矩陣的形式有：

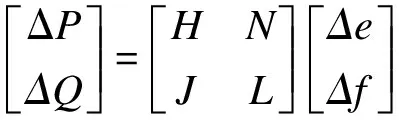
(17)

其中：

H=

(18)

N=

(19)

J=

(20)

L=

(21)

4 算例分析

本文采用IEEE14網絡節點數據為例，用Matlab軟件編寫潮流計算程序，計算的得到的結果與傳統牛頓法潮流計算所得的結果基本一致，傳統牛頓法和基于直角坐標的常雅克比矩陣法潮流計算的電壓幅值比較如圖1所示，由圖可知，在計算誤差允許的范圍內，本文所提的潮流算法是正確的，且與非常數雅克比矩陣的牛頓法相比，算法的雅克比矩陣為常數，避免了在迭代過程中頻繁地計算雅克比矩陣，計算的效率更高。

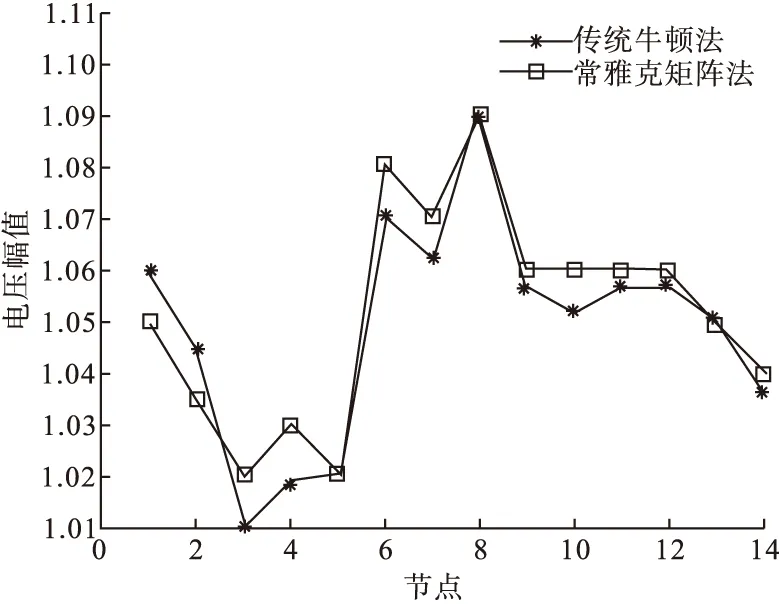
圖1 電壓幅值對比圖

算法的迭代次數為5次，非常數雅克比矩陣牛頓法的迭代次數為3次，這是迭代初值選取的不同引起的，但在每次迭代的計算時間上，本算法比非常數雅克比矩陣牛頓法少。

5 總結

潮流計算是電力系統穩定分析的基礎，數十年來學者們不斷地致力于研究快速、可靠、簡便的潮流計算方法。目前牛頓法求解非線性方程已經是非常方便，在計算非線性的電力系統潮流方程中應用最為普遍，本文在牛頓法的基礎上對雅克比矩陣加以改進，推導出雅克比的常數形式，在計算的過程中把雅克比矩陣的變化量轉換給節點功率的變化量，計算過程更加簡潔方法，收斂速度也更快。電力系統的運行方式以及運行要求在不斷地發生變化，新型電源如不確定性的風電廠、太陽能電廠接入電網后，部分電源的有功和無功值并不確定，這給潮流計算帶來了新的挑戰。潮流計算方法的研究發展在滿足收斂性、快速性、簡潔等基本要求的基礎上，應更多地計及新型電源和設備接入電網后網絡的變化要求，建立合理的潮流計算模型。

[1] 夏沛，汪芳宗.大規模電力系統快速潮流計算方法研究[J].電力系統保護與控制，2012，40(9)：38-40.

[2] 鄭超，盛燦輝，郭小江,等.實用高壓直流輸電穩態模型及潮流算法解析[J].電網技術，2011，35(3):57-62.

[3] 楊鏑.特高壓直流輸電系統可靠性及其對交流系統的影響[D].上海交通大學，2011.

[4] 葉廷路.葛南直流輸電系統的運行與控制[J].電網技術，1994，18(1)：20-25.

[5] 劉崇茹，張伯明.交直流輸電系統潮流計算中換流器運行方式的轉換策略[J].電網技術，2007，31(9):17-21.

[6] 王海超，周雙喜，魯宗相,等.含風電場的電力系統潮流計算的聯合迭代方法及應用[J].電網技術，2005，29(18):59-62.

[7] 雷亞洲，王偉勝，印永華，等.基于機會約束規劃的風電場穿透功率極限計算[J].中國電機工程學報，2002，22(5)：32-35.

[8] 鄭國強，鮑海，陳樹勇.基于近似線性規劃的風電場穿透功率極限的優化算法[J].中國電機工程學報，2004，24(10)：68-71.