卡爾曼濾波在應變式力傳感器中的應用

， ， ，

(同濟大學 機械與能源工程學院，上海 201804)

0 引 言

應變式力傳感器是使用最為廣泛的一種測力傳感器，具有較高的靈敏度和精度，并且適用于靜態和動態測量。由于電阻應變計、傳感器機械本體和信號調理電路的熱噪聲、環境噪聲和電磁噪聲，輸出信號會出現較大的信號漂移，即傳感器在恒定加載時，輸出信號不穩定，波動較大，且不具有明顯規律[1]。隨機噪聲的出現對傳感器的靜動態性能測量精度影響較大，甚至導致無法進行標定。

卡爾曼濾波是一種高效率的自回歸濾波器，能夠從一系列的不完全和包含噪聲的測量中，估計動態系統的狀態[2]。它根據前一時刻的狀態估值和當前時刻的觀測值遞推估計出新的狀態估值，因此，卡爾曼濾波對信號的平穩性和時不變性不做要求，并且不需要存儲歷史數據，適合于實時信號處理。

本文以數字信號處理器(DSP)和A/D轉換器設計的數據采集系統為硬件電路平臺，以實驗室自主研制的應變式單維力傳感器為研究對象，采用卡爾曼濾波算法實現了對傳感器輸出信號的實時濾波，有助于提高傳感器測量精度。卡爾曼濾波程序通過Matlab仿真實現，最后在CCS(code composer studio)開發平臺上進行硬件驗證。

1 卡爾曼濾波原理

1.1 系統方程

卡爾曼濾波的研究對象是隨機線性離散系統，其狀態方程可表示為[3]

Xk=FkXk-1+BkUk+Wk.

(1)

觀測方程為

Zk=HkXk+Vk,

(2)

式中Xk為系統的狀態向量,Fk為狀態轉移矩陣,Bk為輸入控制矩陣,Uk為控制向量,Wk為過程噪聲，其符合均值為0，協方差矩陣為Qk的正態分布,Wk～N(0,Qk)。

Zk為系統的觀測向量,Hk為觀測矩陣,Vk為觀測噪聲，其符合均值為0，協方差矩陣為Rk的正態分布。Vk～N(0,Rk)。

1.2 濾波過程

卡爾曼濾波器的濾波計算包括2個階段：預測與更新。在預測階段，濾波器使用上一狀態的估計，做出對當前狀態的估計。在更新階段，濾波器利用對當前狀態的觀測值優化在預測階段獲得的預測值，以獲得更為精確的新估計值。假設控制信號Uk=0，則預測狀態方程

(3)

預測誤差協方差為

(4)

更新為

(5)

更新狀態估計為

(6)

更新誤差協方差為

Pk|k=(I-KkHk)Pk|k-1.

(7)

對于力傳感器測量系統，可以認為過程噪聲Wk和觀測噪聲Vk是互相獨立的高斯白噪聲序列，對應的協方差矩陣Qk和Rk可認為是常值Q和R[4]。實際應用中，Q和R可由對象模型和離線采集數據獲得，再根據經驗調整這兩個濾波參數以獲得良好的濾波性能。只要給定濾波初值0和P0，根據k時刻的觀測值Zk就能遞推出此刻的狀態估計值k|k和誤差協方差Pk|k。

2 卡爾曼濾波實際應用

應變式力傳感器數學模型[1]如圖1所示。

圖1 應變式力傳感器測試模型

其中,Uk為傳感器收到的載荷信號，力傳感器彈性體、應變電橋電路和信號調理電路可以等效為一階慣性環節，其傳遞函數為

(8)

力傳感器輸出模擬信號經過A/D轉換為數字量，采樣環節可以簡化為零階保持器

(9)

其中,T為采樣周期。對系統模型進行離散化，即取z變換得

(10)

由圖1的數學模型得

(11)

則

(1-e-aT·z-1)x(z)=(1-e-aT)·z-1u(z).

(12)

對上式作z反變換，得差分方程

Xk=e-aT·Xk-1+(1-e-aT)Uk.

(13)

式(13)與系統狀態方程(1)和觀測方程(2)對比，考慮到實際模型中存在噪聲，得出力傳感器實際工作中的狀態方程和觀測方程如下

Xk=e-aT·Xk-1+(1-e-aT)Uk+Wk,

(14)

Zk=Xk+Vk.

(15)

傳感器彈性體一階固有頻率f=1 700 Hz，則式中a≈f=1 700Hz。采樣頻率f=50 kHz，則

e-aT≈1.

(16)

根據卡爾曼濾波理論，如果系統滿足完全隨機可控性和完全隨機可觀測性，則濾波初值0和P0選擇帶來的影響會隨著遞推次數增加而減少，因此,濾波初值可以根據經驗擬定，不會對濾波結果產生影響,算法流程圖見圖2。

圖2 卡爾曼濾波算法流程

3 硬件電路設計

3.1 測試系統框圖

力傳感器測試系統如圖3所示。以實驗室研制的薄壁柱式單維力傳感器為研究對象，當傳感器受力時，應變電橋輸出差分電壓，經過信號調理電路的放大和濾波，由A/D采樣進入DSP，DSP采集并實時使用卡爾曼濾波算法處理數據，將濾波結果存儲到上位機軟件中。

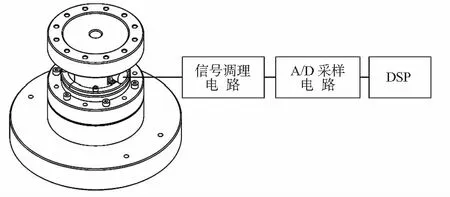
圖3 測試系統框圖

3.2 A/D轉換設計

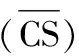
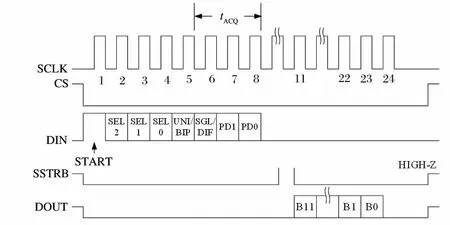
圖4 A/D轉換時序圖

3.3 接口電路設計

McBSP(multichannel buffered serial port)是一種多通道緩沖串行口，擁有二級發送緩沖寄存器和三級接收緩沖寄存器，可對連續的數據流進行操作。可以與IOM-2,SPI,AC97等兼容設備直接連接，支持多通道發送和接收，串行字長度可選。McBSP包括一個數據通道和一個控制通道。數據發送引腳DX負責數據的發送，數據接收引腳DR負責數據的接收，發送時鐘引腳CLKX，接收時鐘引腳CLKR。

TMS320C6416芯片的McBSP在時鐘停止模式時與SPI接口兼容。此時多通道緩沖串口中發送器和接收器內部同步，接收時鐘信號CLKR和發送時鐘信號CLKX在內部相連。McBSP中DX端口數據在時鐘CLKX的上升沿采樣并逐位移入到MAX1281內部移位寄存器，同時A/D轉換的結果在接收時鐘信號CLKR的下降沿由DR腳逐位移入到McBSP內部數據接收寄存器(DRR)中，等待DSP處理。串口電路如圖5。

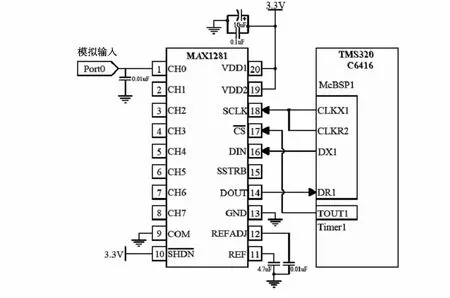
圖5 接口電路

4 實驗與分析

濾波實驗前先將力傳感器固定在標定臺上，以采樣頻率f=50 kHz采集50×103個數據，計算出平均值和方差作為濾波初值0和P0。濾波參數Q反映的是模型噪聲方差，由于模型準確可定為極小值，R反映的是測量方差，由采集的50×103個數據求得。再根據經驗調整這兩個濾波參數以獲得良好的濾波性能，最終確定Q=1×10-6，R=2.5×10-3。

圖6為傳感器加載800 g砝碼時采樣值濾波前后結果，可見濾波值很好地抑制了隨機干擾噪聲信號，保留了傳感器載荷信號，有助于提高標定精度。

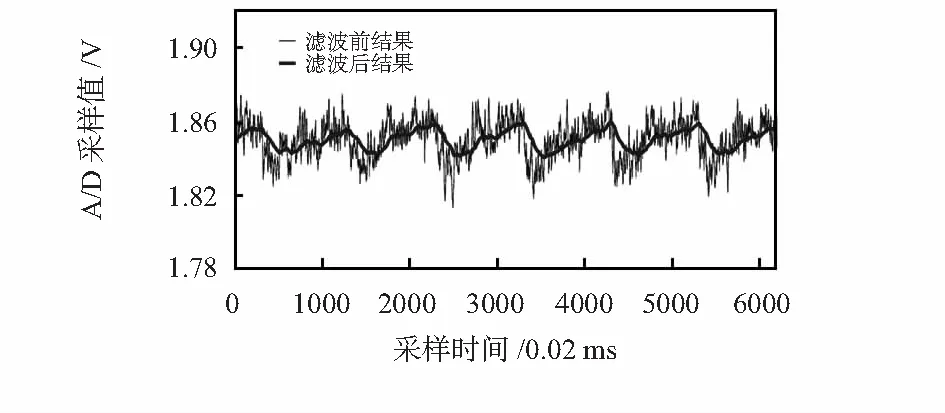
圖6 標定結果濾波前后對比

圖7和圖8為傳感器由800 g加載到1 000 g砝碼時采樣值濾波前后結果，可見卡爾曼濾波也適用于動態加載過程，可應用于傳感器動態性能分析。

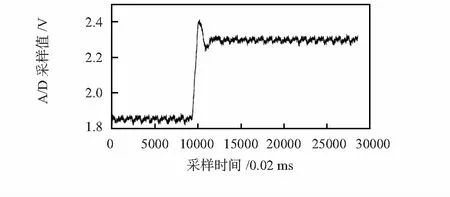
圖7 動態加載濾波前結果

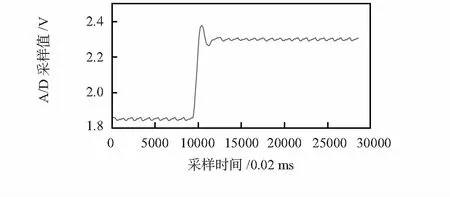
圖8 動態加載濾波后結果

標定實驗時，采用逐級加載和逐級卸載的方法采集6組濾波數據，取均值得到對應的輸入—輸出數據。Matlab編程[5]計算可得V=0.007 8+0.002 3L，非線性誤差為0.271 6 %，滯后誤差為0.130 5 %。擬合結果如圖9所示，可見擬合直線與測量數據點十分接近，即測量范圍內電壓值V與載荷值L具有良好的線性關系。

5 結 論

本文將卡爾曼濾波算法應用到應變式力傳感器信號采

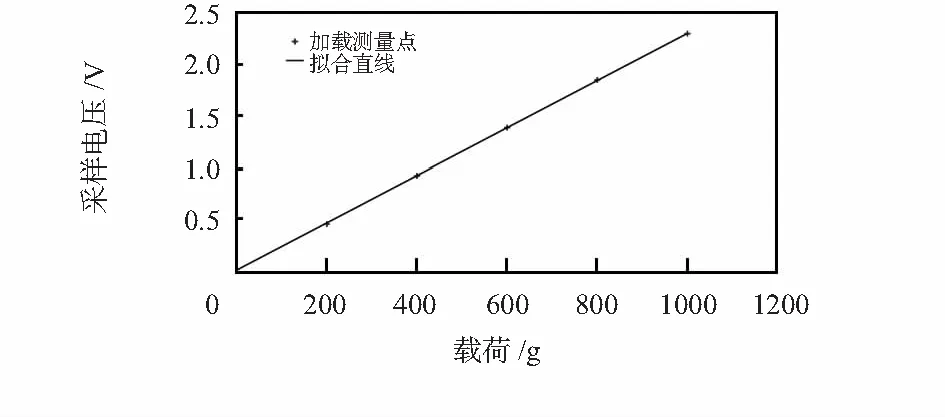
圖9 標定過程擬合曲線

集系統中，實現了高速實時數據處理，可以很好地濾除測量過程噪聲。通過分析傳感器的數學模型，獲得了濾波初值和濾波參數，最后在自主研制的單維力傳感器測試系統上進行了實驗驗證。結果表明:卡爾曼濾波可以抑制隨機干擾噪聲信號，保留傳感器的載荷信號，適用于靜態和動態測量過程，有利于提高傳感器的標定精度。

參考文獻:

[1] 許德章,葛運建,高理富.機器人多維力傳感器標定Kalman濾波[J].電子測量與儀器學報,2006(1):100-105.

[2] 鄒振宇.基于DSP的Kalman濾波器的算法研究[D].成都:成都理工大學,2012:2-15.

[3] Kalman R E.A new approach to linear filtering and prediction problems[J].Journal of Basic Engineering,1960,82(1):35-45.

[4] 周 倩.車輛組合導航中卡爾曼濾波器的設計及FPGA實現[D].北京:北京交通大學,2009:7-10.

[5] 姬翠翠,朱 華,江 煒.基于Matlab和Origin實現測力傳感器的靜態標定[J].傳感器與微系統,2007(12):111-113.