基于自適應Kriging代理模型的葉型氣動優化設計

余 銳， 周代偉， 竺曉程， 杜朝輝

（1.上海交通大學 航空航天學院，上海200240；

2.上海電氣電站設備有限公司上海汽輪機廠，上海200240）

葉型的氣動設計是現代葉輪機械設計的核心技術.合理高效的葉型是提高葉輪機械性能、降低葉輪機械運行成本的前提條件之一.葉型的優化設計往往要求在滿足各種性能結構約束的前提下改善葉型的氣動參數.目前葉型的氣動外形設計有反設計和優化設計2種方法.反設計需要給出目標壓力分布或表面速度分布，將目標壓力分布轉化為葉型幾何外形是一個比較困難且對經驗有較高要求的問題.隨著優化算法的發展和計算機水平的提高，基于隨機性尋優的優化設計方法被廣泛使用.雖然隨機性優化算法具有良好的全局性、魯棒性及高并行性等特點，但多維大尋優空間導致收斂速度慢是制約該算法應用的主要障礙.建立高效的目標評價方法、合理設計優化參數空間和提高優化算法的尋優效率是應用隨機性優化算法的重要前提.雖然目前大多數透平型線已具有較高的熱力效率，但是作為組成葉片基本單元的型線，對其進行優化設計仍是目前進行三維葉片設計的必要步驟.

基于梯度的優化算法最早被運用于葉片的氣動數值優化設計中.Burguburu［1］采用基于梯度的優化算法耦合N－S求解器對3種葉輪機械葉片進行了優化設計，提高了葉片的效率.然而由于基于梯度的優化算法易陷入局部最優，且難以適應葉片氣動優化設計多模態的特點，因而一些具有較好全局尋優能力的啟發式算法逐漸廣泛應用于優化設計中［2］.Oyama［3］采用遺傳算法對 NASA Rotor67壓氣機葉片進行優化設計，取得了較好的效果.?KSüZ［4］介紹了一種用于三維燃氣輪機葉片的氣動優化設計，采用遺傳算法分別對葉片的氣動效率和扭矩進行單目標優化，結果表明，優化后葉片的氣動效率從83.9%提高到85.9%，扭矩增大了7.6%，完成了對原型葉片的改進.全局尋優的算法需要大量CFD計算，時間耗費巨大，不能滿足實際的氣動設計和工程應用.在設計變量與優化目標間構造近似模型（又稱代理模型）來替代CFD計算進行尋優可以很好地解決上述問題，因此，該方法得到了越來越多的應用［5］.薛亮等［6］采用二次多項式近似模型及改進遺傳算法，省時高效地完成了對NASA Rotor67動葉片葉型的優化設計，使得葉片絕熱效率提高了1.1%.高行山等［7］在渦輪葉片氣動優化時引入近似技術，加速了整個尋優過程，通過對某渦輪葉片的優化分析驗證了該方法的可行性.Mengistu等［8］采用遺傳算法構造優化目標與優化變量間的近似模型，以最大化絕熱效率、壓比和最小化總壓損失為優化目標，對亞音速渦輪葉柵二維流動情況進行優化改進.最后通過4組方案分析了設計參數對葉片氣動性能的影響，得到了更優的葉型.王紅濤［9］對比分析了基于自適應Kriging代理模型的優化算法與小生境微種群遺傳算法，發現基于自適應Kriging代理模型的引入減少了迭代所需調用CFD計算的次數，有效地提高了優化過程的效率.

筆者采用基于自適應Kriging代理模型的近似代理技術建立具有全局尋優能力的優化算法，通過對葉型進行參數化描述，代入RANS方程求解得到葉型氣動性能參數，建立葉型氣動優化設計方法，并以壓力恢復系數為目標函數，使用該方法對某設計工況下的葉型進行了優化設計，驗證了整個優化系統的可靠性，提高了葉型的性能.

1 數值優化方法

一般對于帶有約束條件的優化問題可采用如下表達形式

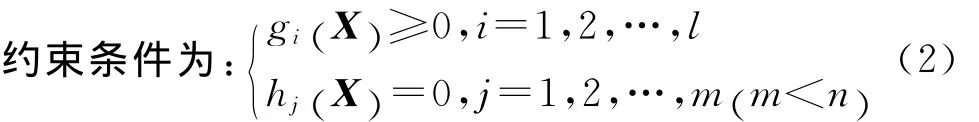
式中：X為設計變量；fopt（X）為目標函數的最優值；X＝［x1，x2，…，xn］T，代表在n維空間Rn中的點，即優化問題中的1組方案；Ω為設計變量的定義域；gi（X）和hj（X）為約束函數.

式（2）中的優化問題需要滿足2種約束條件：不等式約束和等式約束.按照規范化形式，一般都將優化問題歸結為目標函數的于極小值問題，對于目標函數極大化問題可以通過轉換為對應的極小化問題求解.

圖1給出了基于自適應Kriging代理模型的葉型氣動優化設計流程示意圖.由圖1可知，該系統以調節葉型形狀的控制參數作為設計變量，通過試驗設計（DOE）獲得初始的設計變量樣本集.并在完成對葉型網格的自動生成和流場的求解分析后，獲取目標函數信息（即響應樣本集）.進而采用自適應Kriging代理模型構造變量和響應間的近似模型，完成校正點的尋找和評估.若不收斂，將校正點和對應響應值加入樣本庫，不斷更新代理模型直至收斂，獲得目標函數最優的葉型.該系統將試驗設計、CFD數值模擬和優化設計方法相結合，自動完成各模塊間的數據傳遞，減少了人工干預且極大地提高了葉型開發效率.

圖1 基于自適應Kriging代理模型的葉型氣動優化設計流程Fig.1 Flowchart of airfoil aerodynamic optimization design based on adaptive Kriging surrogate model

1.1 優化算法

全局優化算法（如遺傳算法等）雖然可以使優化問題避免陷入局部最優，但由于耗時巨大，難以直接應用于實際工程優化設計中.因而采用代理模型代替數值模擬手段是一種行之有效的方法，可以大大減少優化過程的計算量、提高優化效率及優化算法的性能和組成更好的優化策略.

常用的代理模型主要有多項式響應面模型、徑向基函數模型和Kriging模型等.筆者對葉型優化時選取的算法是一種基于自適應Kriging代理模型的自適應序貫優化算法［10］.由于Kriging模型在訓練樣本點處滿足無偏估計，具有良好的高度非線性近似能力，因此最適合在葉型優化等高度非線性優化問題中作為代理模型使用.

Kriging模型假設樣本點x（維數為m）與對應響應值y之間的關系為

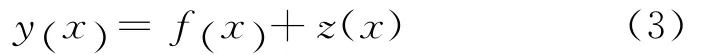
式中：f（）x為確定性部分，可以用一個常數表示，是對設計空間的全局近似；z（x）為一隨機過程，表示對全局近似的背離.

該隨機過程與全局模型的局部偏差是由相關函數反映的.z（x）具有期望為0，方差為σ2的統計特征.方差σ2反映了試驗的精度，一般σ2越大，表示試驗誤差越大.隨機過程z（x）的協方差為：

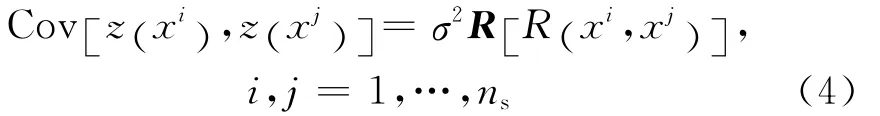
式中：R為相關函數矩陣；ns為樣本點個數；R （xi，xj）為點（xi，xj）間的相關函數，此相關函數為高斯函數.

相關函數的形式如下：

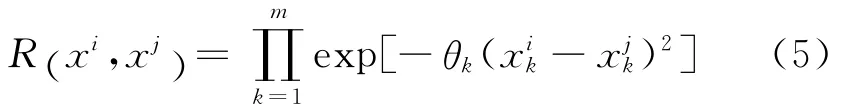
式中：θk為各向異性參數.

在預測點x0處的預測響應值和預測標準差分別為

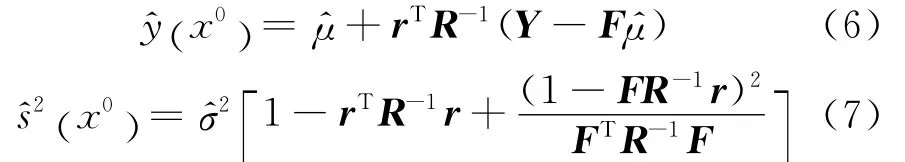
相關函數R （xi，xj）及和均依賴于各向異性參數θ，因而構建Kriging模型的關鍵在于θ的求解，通常由極大似然估計給出，即在θ＞0的情況下使式（8）取得極大值.通過求解得到各向異性參數θ后，即完成了整個Kriging代理模型的構建.

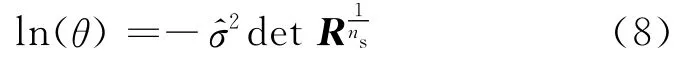
1.2 參數化葉型

對葉型進行參數化表達是實現自動優化設計的前提，一般二維葉型的參數化主要有2種方法：中弧線加厚度分布和采用構造曲線直接對葉型壓力面、吸力面型線進行參數化.目前常用的構造曲線主要有3種：Bézier曲線、均勻有理B樣條曲線和非均勻有理B樣條即NURBS曲線［11］.其中Bézier曲線由于形式簡單、易操作，在參數化中得到廣泛應用.

采用2段Bézier曲線分別對某渦輪葉型壓力面和吸力面型線進行參數化，共有16個控制點控制葉型形狀.其中位于原點處的控制點為2段Bézier曲線的公共點，吸力面型線由自公共點順時針連接的10個控制點獲得，而壓力面型線由自公共點逆時針連接的7個控制點獲得.圖2為葉型型線及對應控制點連線示意圖，其中x和y分別表示葉型的軸向和周向位置.對葉型進行氣動優化設計時，通過改變控制點位置即可生成新的葉型，直到獲得設計變量空間下目標函數最優時的葉型，完成葉型優化改進.

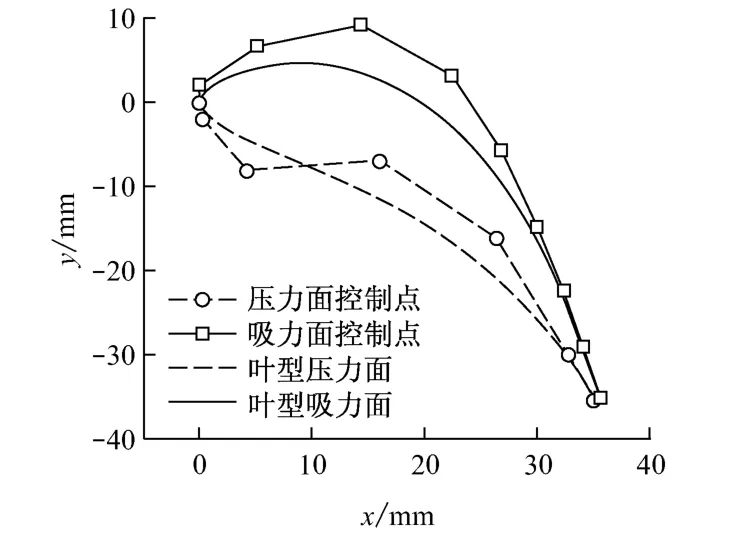
圖2 葉型型線及對應控制點連線Fig.2 Profile of the airfoil and polyline of airfoil control points

1.3 數值方法

在網格生成時選用HOH型拓撲結構：進口段為H型結構化網格，葉型處為O型結構化網格，考慮到實際流動情況，出口段選擇I型網格.對近壁面處網格進行加密，使葉片壁面第1層網格滿足y＋＜10.圖3給出了葉型前緣和尾緣處的網格.

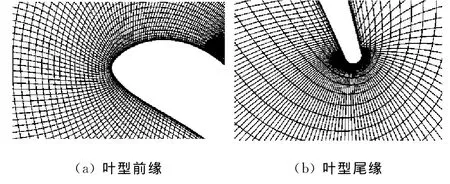
圖3 葉型前緣和尾緣處的網格Fig.3 Mesh for the leading and trailing edge of airfoil

對要進行氣動優化研究的渦輪葉型構造平面葉柵，葉柵柵距為50mm.數值計算時給定進出口邊界條件，其中進口處給定平均總壓為2×106Pa，進口總溫為573K，進口來流氣流角為5°；在出口處給定平均靜壓，使得出口靜壓與進口總壓比為0.896.湍流模型選擇一方程的Spalart－Allmaras湍流模型（即S－A湍流模型），空間離散采用二階精度的迎風格式，時間項推進采用四階Runge－Kutta法加速迭代求解.最大迭代步數設為5 000，收斂標準設為全局殘差降到10－6以下.

為驗證本文數值方法的可靠性，選取文獻［12］中出口氣流角為67°的直葉片進行校核.該文獻采用試驗手段和理論計算對不同出口氣流角的葉柵進行氣動性能的研究，給出了詳細的葉片幾何數據和試驗數據.根據上述數據生成葉柵網格，采用S－A湍流模型和二階精度的迎風格式在設計工況下進行數值模擬.圖4給出了中徑處葉片表面臨界速度比沿相對軸向弦長的分布對比.由圖4可以看出，數值計算所得結果與試驗數據吻合較好，從而驗證了數值計算方法的可靠性.

圖4 中徑處葉片表面臨界速度比分布對比Fig.4 Comparison of surface critical velocity ratio at mid－span height between experimental and numerical data

2 渦輪葉型優化設計

采用2組Bézier控制點控制型線變化，其中O點為壓力面型線和吸力面型線的公共控制點，如圖5所示.在生產實踐中，常通過微調葉片的頭部型線來滿足不同設計要求下進出口流動角的變化，為此需要研究工程設計中對頭部型線的微調是否合理及是否存在最優頭部型線.以對葉型頭部控制點的優化為例，采用上述氣動優化設計方法，研究其對葉型氣動性能的優化設計.設定原始葉型控制點A和B到O點的距離分別為R1和R2，控制點變化后對應的距離為r1和r2.優化時為保證葉型幾何進氣角不變，只改變OA和OB2段控制線的長度而不改變其角度，即以系數矩陣L作為設計變量，以壓力恢復系數ξ最大為優化目標進行葉型的優化設計.

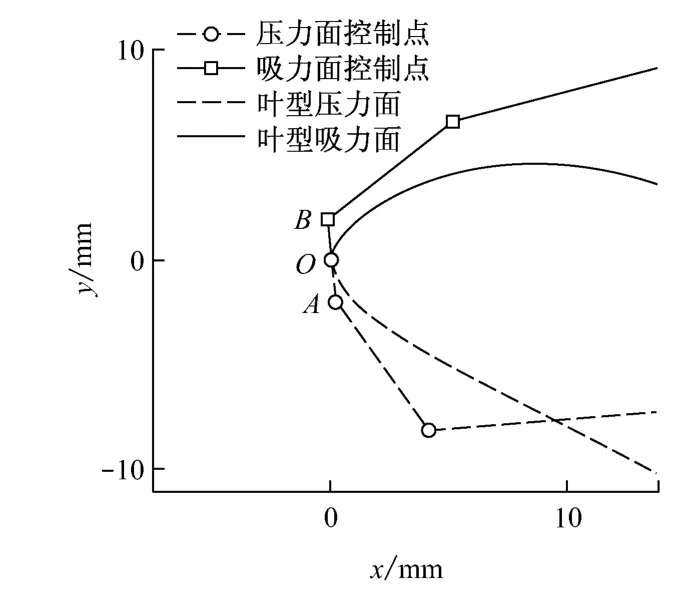
圖5 葉型前緣控制點Fig.5 Control points at leading edge of profile

系數矩陣L與壓力恢復系數ξ的定義如下式中：p01和p02分別為平面葉柵進口和出口的總壓；p2為出口靜壓.

渦輪葉型氣動優化問題可以用式（11）來表示

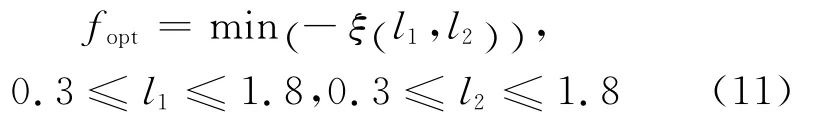
利用試驗設計方法和U＊10（108）均勻設計表生成10個初始樣本點，使樣本點在試驗空間里均勻分布，并構造初始化代理模型，進而對優化目標進行尋優.圖6給出了整個優化過程中響應值隨迭代步數的變化.

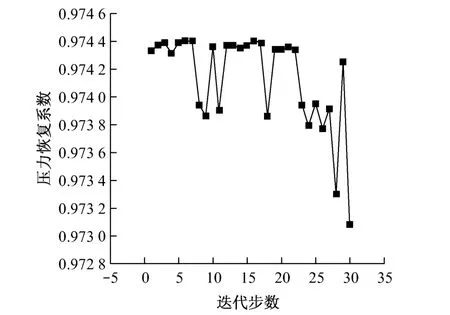
圖6 響應值隨迭代步數的變化Fig.6 Response of pressure recovery coefficient to iteration step

設計工況下原始葉型的壓力恢復系數ξ0＝0.973 76，通過優化迭代后得到當設計變量L＝［1.800 000，1.032 544］時，總壓恢復系數達到最大，即ξ1＝0.974 40，壓力恢復系數有所增大.優化結果表明，存在最優頭部型線，但壓力恢復系數增大的程度有限；同時也說明了實際工程設計中所采用的頭部型線微調方法的合理性.圖7給出了優化前后控制點及型線的對比.從圖7可以看出，葉型前緣處控制線段長度優化的主要變化集中在吸力面型線上，壓力面型線整體上保持不變.

為進一步分析葉型前緣型線的變化對流場的影響，圖8給出了原始葉型和優化葉型表面壓力系數Cp沿軸向的分布，其中表面壓力系數Cp定義如下

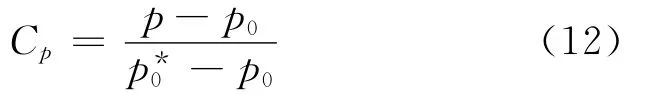
式中：p為當地靜壓；p0為葉柵進口平均靜壓；p＊0為葉柵進口平均總壓.

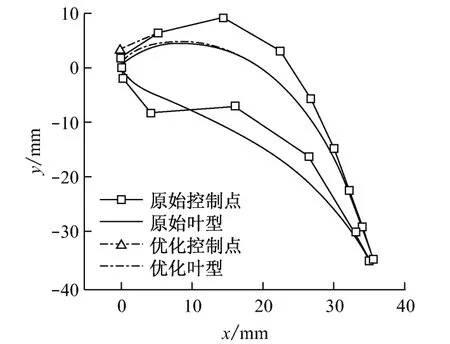
圖7 優化前后控制點及型線的對比Fig.7 Comparison between original and optimized profile

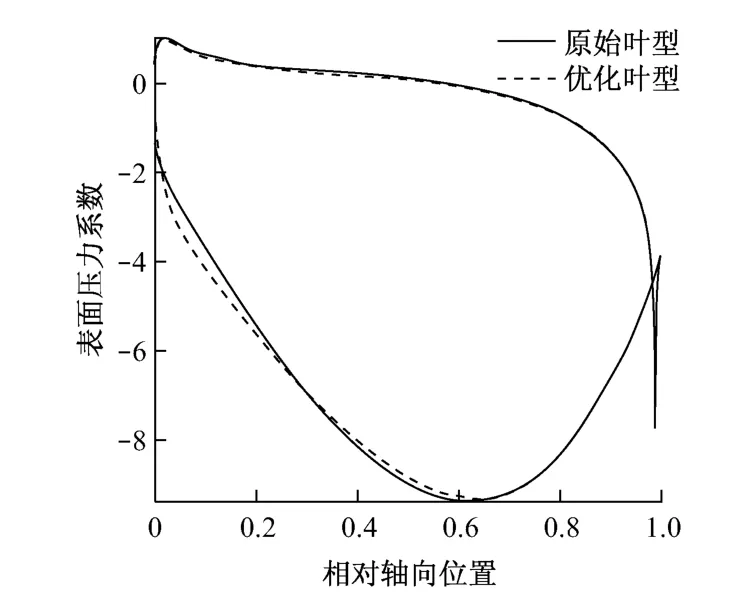
圖8 原始葉型和優化葉型表面壓力系數沿軸向的分布Fig.8 Comparison of pressure coefficient between original and optimized airfoil

從圖8可以看出，優化前后葉型壓力面上的表面壓力系數分布規律基本一致；而在吸力面上存在明顯的差異，優化葉型靠近前緣吸力面處的表面壓力系數較小，氣流沿吸力面流動時壓力變化較平緩.葉型前緣變化引起的流動變化使得葉型型面損失減小，壓力恢復系數有所增大，達到了優化葉型、提高葉柵性能的目的.

3 結 論

基于自適應Kriging代理模型，設計開發了一套集參數化建模、優化算法和數值求解于一體的自動葉型氣動優化設計系統.利用該系統對某渦輪葉型頭部型線進行了優化設計，使原始葉型的壓力恢復系數進一步增大，結果表明存在最優頭部型線，說明了工程實踐中對頭部型線調整的合理性.經過優化改善了葉型的性能，同時也驗證了整個優化系統的可靠性，為葉片的全三維優化設計、提高葉片及級性能的研究奠定了基礎.

［1］BURGUBURU S，TOUSSAINT C，BONHOMME C.Numerical optimization of turbomachinery bladings［J］.Journal of Turbomachinery，2004，126（1）：91－100.

［2］ZHOU Fangzhen，FENG Guotai，JIANG Hongde.The development of highly loaded turbine rotating blades by using 3doptimization design method of turbomachinery blades based on artificial neural network＆genetic algorithm［J］.Chinese Journal of Aeronautics，2003，16（4）：198－202.

［3］OYAMA A，LIOU M S，OBAYASHI S.Transonic axial flow blade optimization：evolutionary algorithms／three dimensional Navier－Stokes solver［J］.Journal of Propulsion and Power，2004，20（4）：612－619.

［4］?KSüZ?，AKMANDOR˙I.Turbine blade shape aerodynamic design using artificial intelligence［C］／／ASME Turbo Expo.Reno－Tahoe，Nevada：ASME，2005.

［5］王紅濤，竺曉程，杜朝輝.自適應Kriging近似模型及其在二維擴壓器優化設計中的應用［J］.計算力學學報，2011，28（1）：15－19，24.WANG Hongtao，ZHU Xiaocheng，DU Zhaohui.Applications of adaptive Kriging approximation model in two dimensional diffuser aerodynamic optimization design［J］.Chinese Journal of Computational Mechanics，2011，28（1）：15－19，24.

［6］薛亮，韓萬金.基于遺傳算法與近似模型的全局氣動優化方法［J］.推進技術，2008，29（3）：21－26.XUE Liang，HAN Wanjin.Global aerodynamic optimization method using genetic algorithms and surrogate model［J］.Journal of Propulsion Technology，2008，29（3）：21－26.

［7］高行山，韓永志，張娟，等.基于近似技術的渦輪葉片氣動優化設計［J］.計算力學學報，2008，25（6）：874－877.GAO Hangshan，HAN Yongzhi，ZHANG Juan，et al.Blade aerodynamic optimization design based on approximation method［J］.Chinese Journal of Computational Mechanics，2008，25（6）：874－877.

［8］MENGISTU T，GHALY W，MANSOUR T．Aerodynamic shape optimization of turbine blades using a design－parameter－based shape representation［C］／／ASME Turbo Expo．Montreal，Canada：ASME，2007．

［9］王紅濤．汽輪機低壓排汽系統內部流動及其氣動優化設計研究［D］．上海：上海交通大學，2011．

［10］王紅濤，竺曉程，杜朝輝．基于Kriging代理模型的自適應序貫優化方法［J］．計算機工程與應用，2009，45（26）：193－195．WANG Hongtao，ZHU Xiaocheng，DU Zhaohui．A－daptive sequential optimization algorithm based on Kriging surrogate model［J］．Computer Engineering and Applications，2009，45（26）：193－195．

［11］樂英，王璋奇，韓慶瑤．基于非均勻有理B樣條曲面重構汽輪機扭曲葉片［J］．動力工程學報，2010，30（12）：926－931．YUE Ying，WANG Zhangqi，HAN Qingyao．Reconstruction of turbine blade twisted based on NURBS surface［J］．Journal of Chinese Society of Power Engineering，2010，30（12）：926－931．

［12］SCHWAB J R．Aerodynamic performance of high turning core turbine vanes in a two－dimensional cascade［C］／／AIAA／SAE／ASME 18th Joint Propulsion Conference．Cleveland，Ohio：AIAA，1982．