正弦激勵法在傳感器校準中的新應用*

楊雪松， 李長春， 母東杰， 陳 策

(北京交通大學 機械電子控制工程學院，北京 100044)

0 引 言

國家標準GB 7665—87對傳感器的定義是：“能感受規定的被測量件并按照一定的規律(數學函數法則)轉換成可用信號的器件或裝置，通常由敏感元件和轉換元件組成”。因而傳感器校準的本質是通過分析被測量的實際值與傳感器輸出來確定這種規律(數學函數法則)。當然受測量手段精度的限制和隨機噪聲的影響，被測量的實際值是很難獲取的，人們往往是以足夠精度的測量值替代之。于是選擇怎樣一種方法來獲取該測量值成為了傳感器校準的關鍵問題之一。

以速度的測量為例，常見的方法有空間濾波器法、相關法、利用多普勒效應或電磁感應原理、加速度積分法和位置微分法。文獻[1]采用瞬時平均速度獲得近似的標準速度，本質上屬于空間濾波器方法，獲得的速度實際上是極短時間段內平均速度而非瞬時速度。再以加速度傳感器的校準為例，目前主流的校準方法有振蕩校準法和沖擊校準法。其中,振蕩校準法即正弦激勵方法，是一種較為簡單且精度又高的校準方法[2]，因此,該方法作為一種標準方法被包含在ISO 16063—11(基于激光干涉儀的絕對振動校準法)中，并得到廣泛的運用[3]。相比于振蕩校準法，沖擊法更適用于高gn值的加速度傳感器校準，且在高頻段的相位不確定度更小[4]。這2種方法的優點是可以對傳感器進行高精度的動態標定，缺點是必須使用激光干涉儀，成本高不易推廣。

本文采用的速度傳感器校準方法是正弦激勵法，實驗平臺采用電液位置伺服系統，該平臺具有結構簡單、成本低、易于推廣的特點。信號處理方法采用基于最小二乘的正弦逼近方法，該方法不僅能夠得到真正意義上的瞬時速度信號，而且能夠在存在噪聲的情況下取得最優解。

上述方法還可以被應用到測量定回轉軸角加速度的問題中。長期以來，由于角加速度傳感器的成本遠高于線加速度傳感器，因此,工程人員期望找到一種用線加速度傳感器測量角加速度的方法。經過多年的發展，國內外學者分別提出了六加速度計、九加速度計和十加速度計的組合方法[5]來獲取剛體在所有自由度方向上的運動狀態。不過在一般的機電系統中定軸回轉的狀態是最為常見的，文獻[6]提出了一種用2只雙軸線加速度計獲取定軸回轉狀態的方法。相比之下，在適當的假設條件下，這種改進的正弦逼近算法可以實現用一只單軸加速度計來完成角加速度的測量，顯然該方法是更經濟實用的。

1 校準算法

校準算法的核心是基于最小二乘法的正弦信號逼近方法，文獻[7]提出了一種辨識正弦信號幅值和相位差的方法。但是，實際的傳感器信號常包含有偏置，使得上述方法不再適用，因此，本算法在原算法的基礎上加入了偏置項的辨識，大大提高了計算精度。

假設有一正弦信號v(t)被以采樣頻率fs采樣，得到一組M個采樣點。待辨識的信號如下

v(t)=Vsin(ωt+φ)+W.

(1)

展開上式可得

v(t)=C0sinωt+C1cosωt+C2.

(2)

其中，C0=Vcosφ,C1=Vsinφ,C2=W。

需要確定的參數為C0，C1，C2，為此需要應用最小二乘法得到該參數的最小二乘估計。假設采樣頻率為fs，得到M個采樣點，通過采集系統可得采樣點的值v(t0)，v(t1)，…，v(tM-1)，可得到v(t)的測量殘差為

vi=C0sinωti+C1cosωti+C2-v(ti),

i=0,1,…,M-1.

(3)

其殘差平方和為

(4)

令Φ0(t)=sinωt，Φ1(t)=cosωt，則有

(5)

根據最小二乘原理，由極小值存在的必要條件，求殘差平方和[v2]的極小值，可由式(5)求出對Cj(j=0,1,2)參數的偏導數，并令其為0，如式(6)所示

(6)

由上式可獲一個方程組，這一方程組的解即為參數Cj的最小二乘估計。為此，根據式(6)可導出方程組

(7)

式中Φ0=Φ0(ti),Φ1=Φ1(ti)。為便于計算可以將方程組(7)寫成矩陣的形式

ATAC=ATb.

(8)

其中

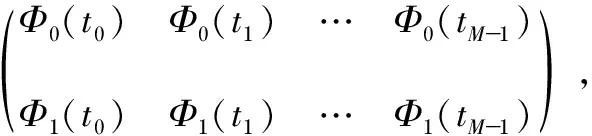
CT=[C0C1C2]，

bT=[v(t0)v(t1) …v(tM-1)].

若式(8)中的ATA為非奇異矩陣，則C必有唯一解，其矩陣表達式為

C=(ATA)-1ATb.

(9)

綜上所述，通過最小二乘法可以辨識出參數Cj，進一步可以推導出正弦信號的幅值、相位以及偏置。

2 實驗研究

為證明上述算法的有效性，分別設計了使用位移傳感器標定速度傳感器的試驗和利用線加速度測量定回轉軸角加速度的實驗。

2.1 實驗一

實驗系統由：閥控液壓缸、傳感器、數據處理系統組成，如圖1所示。實驗開始后，閥控液壓缸在控制系統的閉環控制下進行正弦運動，數據采集系統采集位置傳感器信號和速度傳感器信號，再利用正弦信號參數辨識算法分別得到位置信號和速度信號的幅值Ap,As,則速度傳感器的靈敏度S(V/(m·s-1))可由式(10)得到

(10)

其中,Ap的單位是m，As的單位是V，因為正弦位置信號的導數是頻率相同但幅值增大了ω倍的余弦信號，因此，在這里ω是一個無量綱比例系數，數值上等于信號的角頻率。

圖2展示了一組實驗過程中位置與速度傳感器的信號，如圖所示位置信號的信噪比大，速度信號的信噪比小，因此，先利用正弦信號參數辨識算法去除噪聲的影響，而后利用較理想的位置信號的微分值校準速度傳感器的靈敏度是合理的。校準結果如表1所示，為方便計算表中的幅值Ap，As使用dB為單位，不影響計算結果。對實驗數據求平均得到該速度傳感器的靈敏度S為0.136 8(V/(m·s-1))，其標準差為0.000 55，因此，該校準方法具有較高的精度。

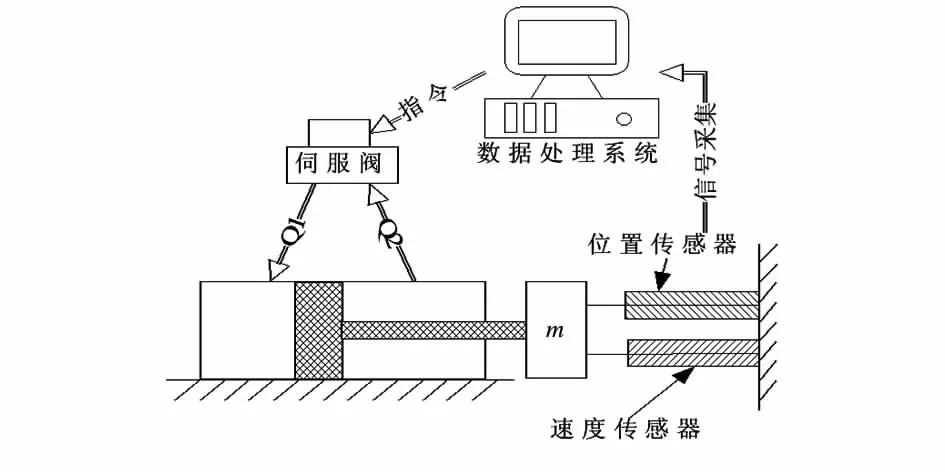
圖1 實驗一系統組成示意圖

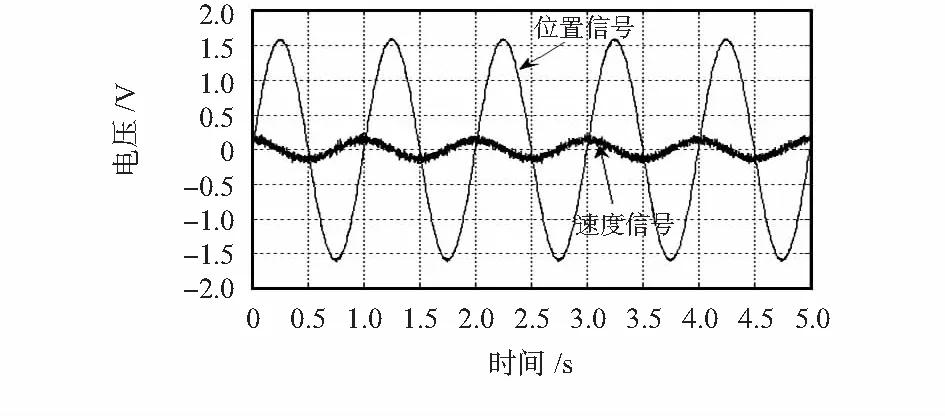
圖2 頻率1 Hz的正弦激勵下的傳感器信號

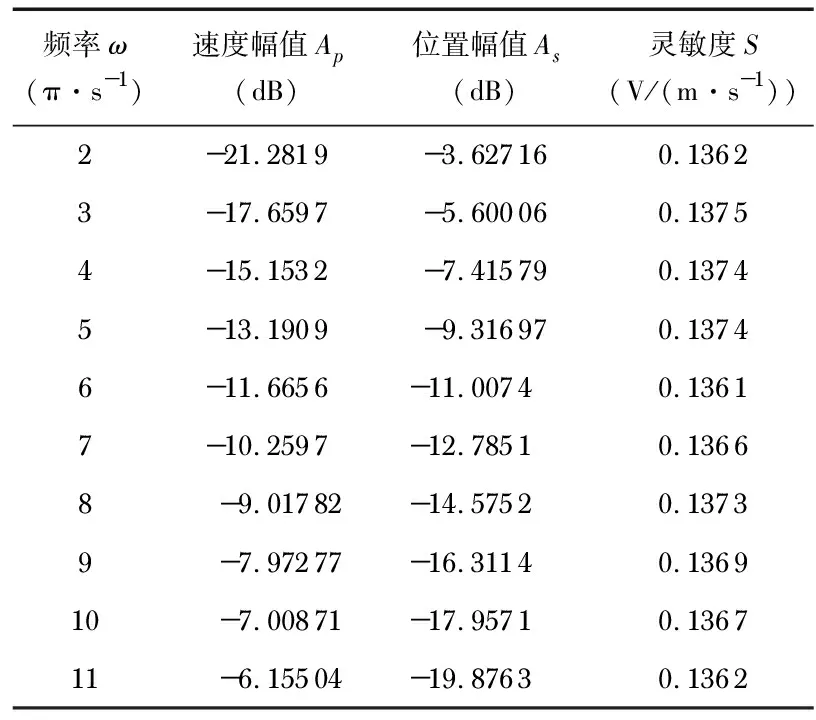
表1 各頻率點速度傳感器靈敏度校準結果

2.2 實驗二

當線加速度計被安放在定回轉軸的切線方向上時，線加速度計就可以測量出角加速度。不過當該回轉軸平行于大地(或者說除非其垂直于地面)時，重力加速度就會在切線方向產生一個分量，如圖3所示，該分量是轉角θ的正弦函數gsin(θ+π/2)，在角加速度的測量中應當將其去除。試驗系統由伺服電機、單軸線加速度計、測控系統組成。首先測控系統發出指令使伺服電機勻速轉動，實時采集伺服電機反饋的轉角信號和加速度計的反饋信號,令θ=ωt，其余算法與第二部分介紹的校準算法一致，即可得到由重力產生的加速度信號與轉角的函數關系，如式(11)所示。從而可以根據此函數關系對重力加速度的切線方向分量進行補償。圖4顯示了當電機回轉軸進行勻速轉動時，加速度信號補償前后的情況，補償效果非常理想。

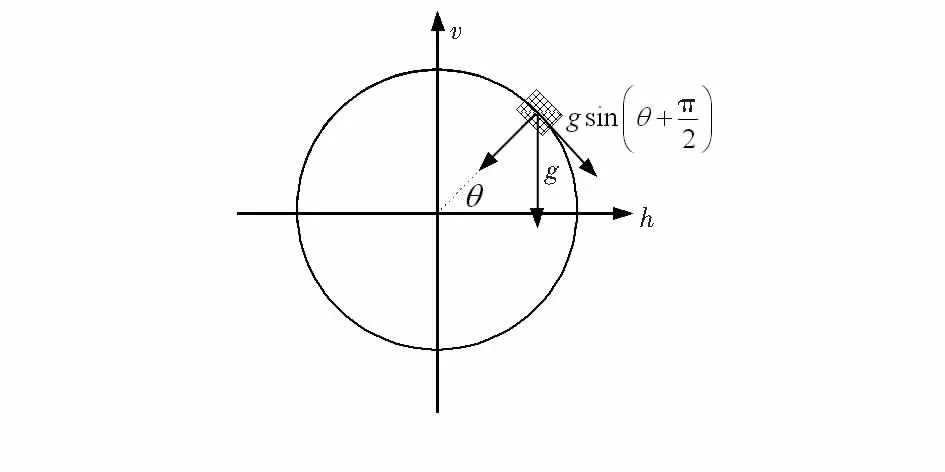
圖3 重力加速度切線分量與轉角關系圖

g′(θ)=Agsin(θ+φg)+Wg,

(11)

式中g′為線加速度傳感器繞回轉軸勻速轉動時輸出的信號，Ag,φg,Wg分別為該函數的幅值、初始角和偏置。

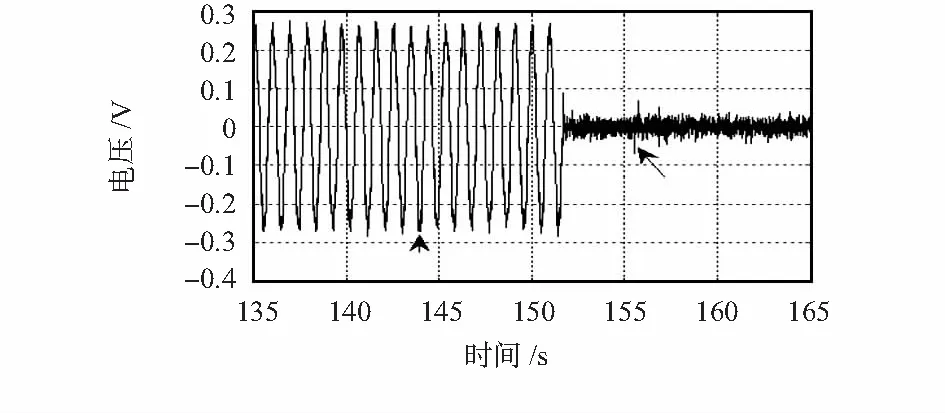
圖4 回轉軸勻速轉動時加速度信號對比圖

3 結 論

1)實際的傳感器信號常存在零位漂移，因此,新的正弦逼近算法在老算法的基礎上增加了對信號偏置量的辨識。該方法可適用于各類型的速度、加速度傳感器的靜態靈敏度校準，實驗結果表明,該方法具有很高的精度。

2)該方法可用于補償重力加速度對于繞定回轉軸轉動的線加速度的影響，從而可以使單軸線加速度具備測量角加速度的能力，實驗結果表明:該方法獲得了極佳的補償效果。

參考文獻:

[1] 李亞榮，付繼華.絕對式線速度傳感器標定系統原理與實現[J].大連鐵道學院學報,2003，24(1):93-95.

[2] 大畑正已，吳 凡.壓電式加速度傳感器的校準方法[J].國外計量，1988(5)：23-24.

[3] Veldman C S.A novel implementation of an ISO standard method for primary vibration calibration by laser interferometry[J].Metrologia，2003,40:1-8.

[4] Link A，Taubner A， Wabinski W，et al.Calibration of accelero-meters:Determination of amplitude and phase response upon shock excitation[J].Measurement Science & Technology，2006,17:1888-1894.

[5] 費 維，劉正士，鄭傳榮.幾種角加速度傳感器的工作原理及其應用[J].機床與液壓，2005(1):145-146.

[6] 陶建峰，劉成良，王旭永.用線性加速度計測量定軸回轉系統狀態的理論研究[J].上海交通大學學報，2006，40(4):553-557.

[7] 程 捷.檢測正弦信號相位差算法的研究[J].計量技術，1997(10):28-30.