基于Fisher信息距離的被動傳感器目標協(xié)同跟蹤方法

王 勇

(1.中國礦業(yè)大學 信息與電氣工程學院，江蘇 徐州 221116；2.徐州工業(yè)職業(yè)技術學院，江蘇 徐州 221140)

0 引 言

隨著現(xiàn)代戰(zhàn)爭的需要和傳感器技術的迅速發(fā)展，多傳感器數(shù)據(jù)融合技術得到了廣泛的應用。在現(xiàn)有的多傳感器目標跟蹤系統(tǒng)中， 傳感器的多樣性和信息來源的廣泛性和復雜性，不僅限制了對傳感器信息資源的有效利用，而且嚴重影響了傳感器的合理使用。因此，研究對有限的傳感器資源進行科學合理的分配，實現(xiàn)多傳感器的協(xié)同探測已成為目前亟待解決的問題[1]。

從信息論的角度出發(fā)，當傳感器對目標定位時或被跟蹤目標的狀態(tài)估計的精確度提高時目標的信息有所增加，即通過傳感器對目標的觀測使目標的位置估計得到更新，從而減少了目標位置的不確定性。文獻[2]在對目標的狀態(tài)估計過程中，將信息增量的含義推廣為在獲得新的量測條件下，定量表述目標狀態(tài)不確定性的改變，并且將信息熵定義為估計誤差協(xié)方差矩陣形式。文獻[3]則根據(jù)Rényi差異求得信息增量，并基于此解決了大規(guī)模動態(tài)網絡的傳感器資源管理問題。文獻[4]通過貝葉斯網絡建立量測過程模型，采用分辨力增量實現(xiàn)異類傳感器融合中目標分類的最優(yōu)化。文獻[5]針對傳感器網絡中機動目標跟蹤問題，提出了一種基于Rényi信息增量的機動目標協(xié)同跟蹤方法。文獻[6]利用信息增量對被動傳感器資源分配算法進行了研究。最近，文獻[7]利用信息幾何理論，以Fisher信息距離來定義目標之間的區(qū)分度，并直接依據(jù)目標之間的區(qū)分度制定傳感器資源分配策略。

本文針對多被動傳感器目標跟蹤問題，在無跡卡爾曼粒子濾波算法的框架下，利用Fisher信息距離來計算觀測到來之前的先驗概率密度函數(shù)和獲得觀測后的后驗概率密度函數(shù)之間的信息增量，選擇信息增量最大的傳感器進行目標跟蹤。仿真實驗表明:本文所提算法能夠顯著提高目標的跟蹤精度，實現(xiàn)協(xié)同跟蹤。

1 Fisher信息距離

1.1 基本理論

考慮如下概率分布族

P=p(x;ζ).

(1)

其中,x為隨機向量，ζ=(ζ1,ζ2,…,ζn)為概率分布的參數(shù)，它是一個包含n個元素的向量。每一個參數(shù)ζ對應一個概率分布p(x;ζ)。從幾何的觀點來看，概率分布族P可以看做高維空間中的n維流形。在統(tǒng)計流形中，流形上的每一個點代表了一個概率分布函數(shù)，因此，概率密度函數(shù)之間的差異可以用流形中點之間的距離來度量,通常采用隨機變量的Fisher信息作為度量張量,其定義如下[7]

(2)

其中，ζ1和ζ2分別對應概率密度函數(shù)p(x;ζ1)和p(x;ζ2)，則概率密度函數(shù)p(x;ζ1)和p(x;ζ2)之間的距離即為統(tǒng)計流形中對應點ζ1和ζ2之間的距離；[gij]為Fisher信息矩陣，各元素定義如下

(3)

此處E[·]表示關于p(x)的期望，也就是

(4)

在信息幾何理論中，由于每個概率分布函數(shù)都被抽象為統(tǒng)計流形上的一個點，潛移默化實現(xiàn)了“去隨機性”。因此，信息幾何有潛力將統(tǒng)計學中的隨機性問題變?yōu)橐粋€確定性問題來求解，實現(xiàn)現(xiàn)有方法的革新。

1.2 Fisher信息距離的計算

直接計算Fisher信息距離需要大量的計算資源。本文采用文獻[7]給出的基于完全的Isomap(isometric feature mapping)算法的Fisher信息距離近似求解方法。結合本文背景，具體算法步驟如下

2)對距離矩陣DG進行初始化

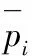
(5)

由于本文是在無跡卡爾曼粒子濾波的框架下進行跟蹤，故

(6)

其中，wk為k個粒子的權值，p(z|xk)為似然函數(shù)，p(z)為觀測的邊緣分布函數(shù)，其表達式為

(7)

3)對距離矩陣中每個元素依次進行遍歷，用D(i,j),D(i,d)+D(d,j)中較小的值來替換D(i,j),d=1,2,…，M，從而得到距離矩陣DG,并得到DF(p1,p2)。

2 基于Fisher信息的被動傳感器協(xié)同跟蹤

2.1 多被動傳感器資源協(xié)同分配模型

設被動傳感器跟蹤系統(tǒng)中有Ms只傳感器，各被動傳感器使用成本相同且已進行時空對準，每只傳感器能夠探測和跟蹤的最大目標數(shù)為m。這些傳感器構成基本集合為S={1,2,…,Ms}，將集合S的子集全體(除去空集)記為擴展集合D，并記第r個子集為Dr，Dr中所包含的傳感器數(shù)目為Mr，則集合D的每一個元素Dr描述了一種可能的傳感器組合，所有傳感器組合的數(shù)目為2Ms-1。假設在探測區(qū)域內，目標的數(shù)目為N，當傳感器組合Dr分配給目標n時獲得的信息增量為IDin。

建立如下線性規(guī)劃模型

(8)

約束條件：

1)傳感器分配約束

(9)

2)每個目標的最大被跟蹤容量約束

(10)

3)每部傳感器最大跟蹤能力約束

(11)

其中,G為系統(tǒng)總體信息增量和；Ds為傳感器組合總數(shù)。

式(10)給出了每個目標被跟蹤容量約束，式(11)給出了每只傳感器最大跟蹤能力約束，從而確保被跟蹤的目標數(shù)量不超過傳感器的最大跟蹤能力[6]。

2.2 算法實現(xiàn)步驟

多被動傳感器協(xié)同目標跟蹤算法步驟如下：

1)將所有的被動傳感器進行分組；

2)每個傳感器組合利用UPF獲得目標狀態(tài)的先驗概率密度、后驗概率密度函數(shù)；

3)對于每個傳感器組合計算跟蹤不同目標時獲得的Fisher信息增量；

4)建立線性規(guī)劃模型對傳感器資源進行分配，求出滿足約束條件時系統(tǒng)總體的信息增量和最優(yōu)分配方案；

5)輸出最優(yōu)分配方案進行濾波跟蹤。

3 仿真實驗分析

3.1 仿真場景設置

本文所提的算法與無跡粒子濾波與協(xié)方差矩陣相結合的方法進行了比較分析。設觀測區(qū)域x為[0,100]m,y為[0,100]m內隨機分布10只被動傳感器，各傳感器的測角誤差標準差σ相同，且均為1 mrad，系統(tǒng)采樣周期T=1 s，每只傳感器最大跟蹤目標數(shù)為2。3個目標在觀測區(qū)域內做勻速直線運動，運行時間為30 s，目標運動模型采用CV模型，粒子數(shù)為200，蒙特—卡羅次數(shù)為50次。當目標進行運動時，F(xiàn)isher信息距離的求解作為目標跟蹤的一部分融入整個跟蹤濾波遞推過程。圖1給出了仿真實驗的態(tài)勢圖，其中包括3個目標的運動軌跡和被動傳感器系統(tǒng)中10只隨機分布的傳感器位置。

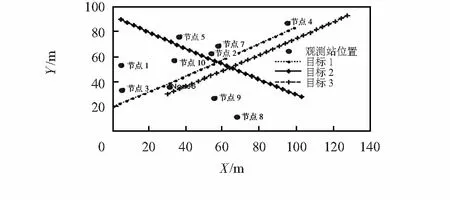
圖1 目標與傳感器分布態(tài)勢圖

3.2 實驗結果與分析

圖2和圖3給出了1次蒙特—卡羅仿真各目標相應的傳感器選擇結果。從仿真結果來看，由于各被動傳感器測角誤差相同，所以，傳感器的選擇一定程度上取決于目標與傳感器的距離。

圖4為50次蒙特—卡羅實驗的均方根誤差曲線圖。從結果可以看出：在跟蹤區(qū)域內，采用本文方法獲得的3個目標的位置誤差均優(yōu)于無跡粒子濾波與協(xié)方差矩陣相結合的方法。這是因為與本文提出的方法相比，在非線性非高斯環(huán)境下，協(xié)方差矩陣表征的只是后驗概率密度函數(shù)的一個特征值，用其來衡量跟蹤精度是不準確的，從而做出的跟蹤傳感器選擇方案亦不是最優(yōu)的。而本文的方法是利用大量粒子來近似先驗概率密度函數(shù)和、后驗概率密度函數(shù)，比較的是概率密度函數(shù)的近似程度，因此，F(xiàn)isher信息距離包含了更多的信息，可以較為準確地描述傳感器對目標跟蹤的貢獻，從而可以在合適時間選擇恰當?shù)膫鞲衅鲗δ繕诉M行精確協(xié)同跟蹤，避免傳感器資源的浪費。因此，本文所給出的算法可以動態(tài)地選擇跟蹤性能較好的傳感器進行跟蹤，從而實現(xiàn)傳感器協(xié)同跟蹤，顯著提高系統(tǒng)的整體跟蹤性能。

3.3 算法時間復雜度分析

表1列出了10只傳感器3個目標50次蒙特—卡羅仿真實驗算法復雜度對比情況，包括算法的平均運行時間和相對計算強度(將協(xié)方差矩陣法計算強度設為1，相對計算強度無量綱)。由表1可看出：所提算法運算時間有了明顯地增加，額外的計算量主要用于計算先驗概率密度函數(shù)和后驗概率密度函數(shù)之間的Fisher信息距離。

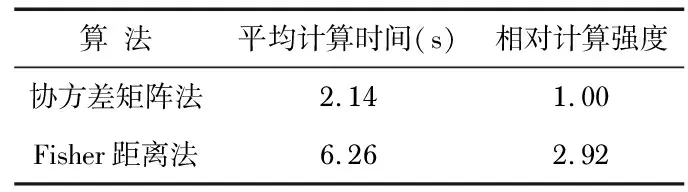
表1 算法計算復雜度

綜合上述實驗結果，本文所提算法可以自適應地選擇跟蹤性能較好的傳感器進行協(xié)同跟蹤，顯著地提高了跟蹤精度，但同時也增加了一定的計算復雜度。

4 結 論

本文針對多被動傳感器協(xié)同跟蹤問題進行了研究，依據(jù)信息幾何理論，以流形中的Fisher信息距離來衡量先驗概率密度函數(shù)和后驗概率密度函數(shù)之間的距離，繼而以此距離為依據(jù)動態(tài)選擇傳感器進行目標跟蹤。與傳統(tǒng)的協(xié)同跟蹤算法相比，能夠更加充分地體現(xiàn)出信息熵的變化。仿真實驗驗證了算法的可行性、優(yōu)越性和動態(tài)環(huán)境中的自適應性。

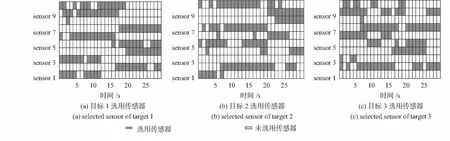
圖2 本文算法傳感器選擇情況

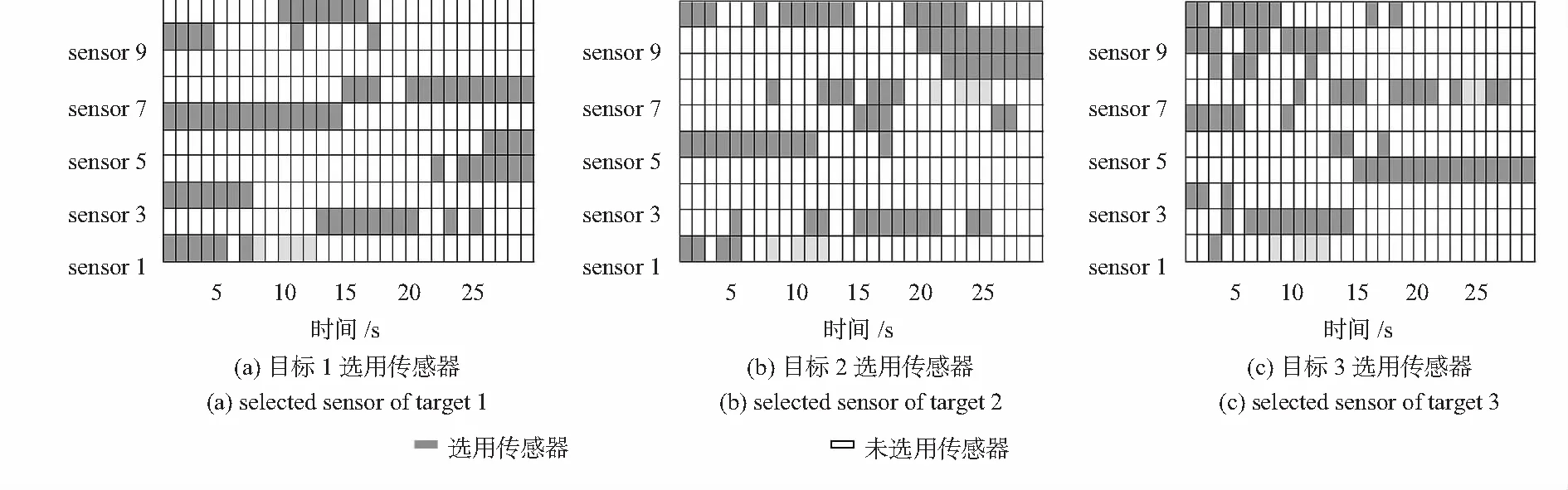
圖3 協(xié)方差法傳感器選擇情況

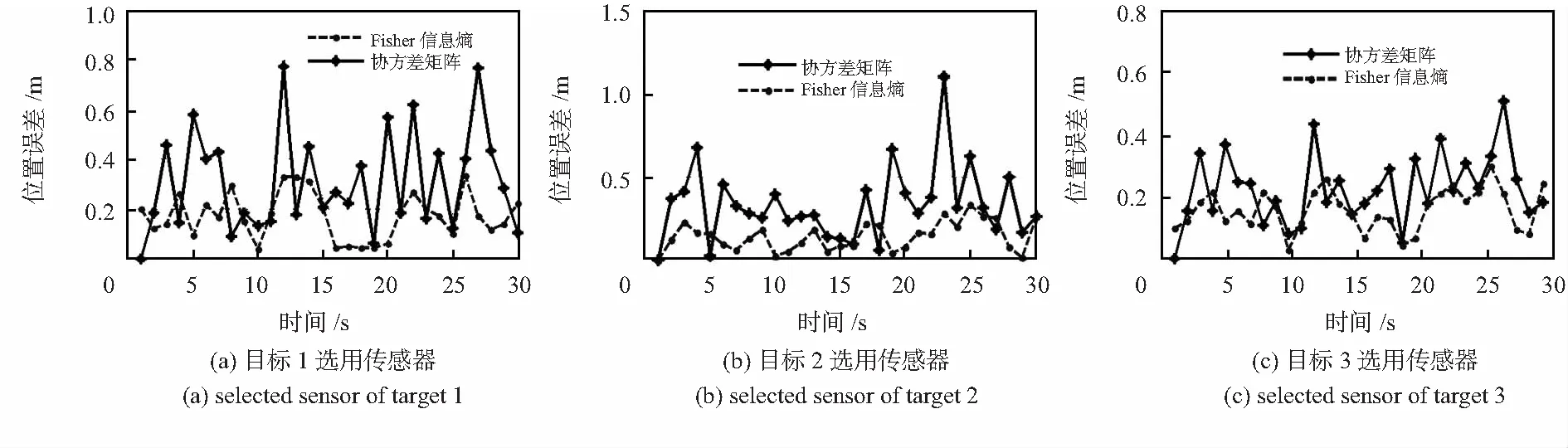
圖4 目標跟蹤位置誤差

參考文獻:

[1] 羅開平，姜 維，李一軍.傳感器管理評述[J].電子學報，2010，38(8):1901-1907.

[2] Hintz K J,Mcvey E S.Multi-process constrained estimation[J].IEEE Trans on Systems,Man and Cybernetics,1991,21(1):434-442.

[3] Kreucher C M,Hero A O,Kastella K D,et al.An information-based approach to sensor management in large dynamic network-s[C]∥Proc of the IEEE,2007,95(5):976-999.

[4] Yang Chun,Kadar Ivan,Blasch Erik.Comparison of information Theoretic divergences for sensor management[C]∥Proc of the SPIE Signal Processing,Sensor Fusion and Target Recognition,2011,8050:1-9.

[5] 劉 欽，劉 錚．一種基于Rényi信息增量的機動目標協(xié)同跟蹤方法[J].控制與決策，2012，27(9):1437-1440．

[6] 李彬彬，馮新喜，王朝英，等.基于信息增量的多被動傳感器資源分配算法[J].系統(tǒng)工程與電子技術，2012,34(3):502-507.

[7] 張華睿，楊宏文，胡衛(wèi)東，等.基于Fisher信息距離的傳感器管理方法[J].系統(tǒng)工程與電子技術，2012，34(8):1587-1591.

[8] Lapuyade-Lahorgur J,Barbaresco F.Radar detection using siegel diatance between autoregressive processed,application to HF and X-band radar[C]∥Proc of IEEE Radar Conference,2008:1-6.