PPP星間單差整周模糊度的固定方法與結果分析*

潘 林 蔡昌盛 朱建軍

(中南大學地球科學與信息物理學院，長沙 410083)

PPP星間單差整周模糊度的固定方法與結果分析*

潘 林 蔡昌盛 朱建軍

(中南大學地球科學與信息物理學院，長沙 410083)

為消除載波相位觀測值中存在的小數偏差項，將消電離層模糊度分解為寬巷模糊度與窄巷模糊度，通過星間單差消除接收機端的寬巷模糊度與窄巷模糊度小數偏差，并利用衛星端寬巷模糊度小數偏差恢復寬巷模糊度的整數特性，而衛星端的窄巷模糊度小數偏差則包含在CNES提供的精密衛星鐘差數據中，應用其鐘差數據也可以恢復窄巷模糊度的整數特性。利用IGS站觀測數據進行分析表明，模糊度固定成整數后，星間單差精密單點定位固定解與非差精密單點定位浮點解相比，定位精度有顯著改善，三維定位精度的最大改善率達63.8%。

精密單點定位;整周模糊度;小數偏差;寬巷模糊度;窄巷模糊度

利用IGS分析中心提供的精密軌道和精密鐘差數據進行精密單點定位(PPP)，可以得到cm級甚至mm級的定位精度［1］。但傳統的PPP中，非差載波相位觀測值中存在源自于接收機和衛星的小數偏差項(FCB，fractional cycle biases)，而且這些小數偏差與非差整周模糊度難以分離［2］，破壞了模糊度的整數特性，致使模糊度只能當作浮點數處理，限制了精密單點定位精度的進一步提高。針對這一問題，目前主要有兩種方法:借助全球或者廣域參考網站的數據，將小數偏差項估計出來［2－6］;從鐘差估計的角度，利用衛星鐘差和接收機鐘差分別吸收衛星端和接收機端的小數偏差項［7－8］。目前用第一種方法得到的小數偏差數據還沒有公布。而第二種方法中，通常采用非差觀測值進行解算，使用吸收了衛星端小數偏差的精密衛星鐘差數據，只進行了衛星端小數偏差改正，并認為在解算過程中，接收機鐘差會吸收接收機端的小數偏差。實際上，接收機鐘差不可能完全吸收接收機端的小數偏差，因而模糊度固定必然會受到接收機端小數偏差項的影響。

本文在將消電離層模糊度分解成寬巷模糊度和窄巷模糊度的基礎上，通過星間單差操作來消除接收機端的寬巷模糊度與窄巷模糊度小數偏差，然后根據CNES提供的衛星端寬巷模糊度小數偏差改正觀測值，以恢復寬巷模糊度的整數特性。而CNES提供的精密衛星鐘差數據在生成的過程中吸收了衛星端的窄巷模糊度小數偏差［9］，因此，應用其鐘差數據也可以恢復窄巷模糊度的整數特性。利用IGS站提供的數據進行分析表明，在模糊度固定成整數后，星間單差PPP固定解與非差PPP浮點解相比定位精度有顯著提高。

1 固定整周模糊度的PPP實施方法

1.1 PPP誤差源與改正方法

1)衛星軌道和鐘的誤差:使用CNES提供的精密軌道和精密衛星鐘差數據，精密軌道的精度優于5 cm，精密衛星鐘差的精度優于0.12 ns，滿足PPP中固定窄巷模糊度的精度要求［9］。

2)電離層延遲:采用消電離層組合消除一階電離層誤差的影響，而高階電離層誤差模型因為復雜且影響較小，在太陽活動不劇烈時可以忽略不計。

3)對流層延遲:對流層延遲值隨高度角在2.4～25 m 之間變化［10］。干分量通過 Hopfield 模型［11］進行改正，濕分量作為未知參數進行估計，使用的投影函數為 Niell［12］。

4)DCB(differential code biases):由于CNES所提供的精密軌道和精密衛星鐘差數據是相對于P碼觀測值的，因此如果用戶觀測文件中使用的是C/A碼觀測值，就必須進行DCB改正。DCB的影響可達1.2 m，約1.4個寬巷模糊度波長，如果不進行DCB改正，可能導致寬巷模糊度固定不準確。IGS分析中心CODE按月提供DCB改正數據［13］。

5)天線相位中心偏差:天線相位中心偏差可達dm級［14］，因此在PPP中必須進行改正。IGS所提供的ATX文件給出了衛星天線相位中心改正與接收機天線相位中心改正的數據。

6)天線相位纏繞:天線相位纏繞對PPP的影響十分顯著，能達到半個波長，如果忽略將使得定位精度只能達到dm級，因此在PPP中必須進行天線相位纏繞改正［15］。

7)固體潮、大洋負荷與大氣負荷:固體潮可以引起徑向30 cm、水平方向5 cm的定位誤差，因此必須進行改正［16］;而大洋負荷和大氣負荷引起的誤差很小［16－17］，在處理過程中可以忽略。

1.2 寬巷模糊度固定

在GPS衛星定位中，常用的觀測值有測碼偽距和載波相位觀測值。對于雙頻接收機，測碼偽距和載波相位觀測值可以表示為:

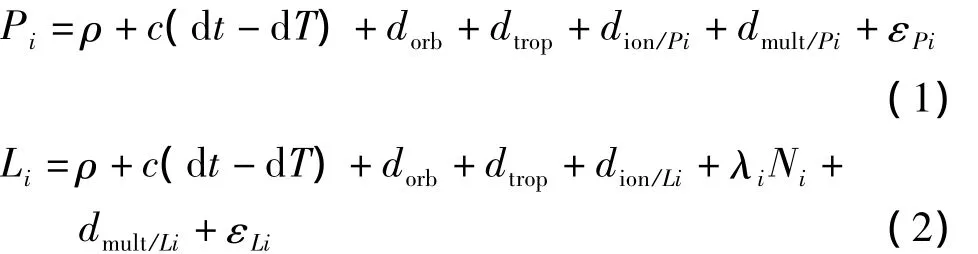
式中，i(i=1，2)表示GPS衛星的兩個頻率，P是偽距觀測值，L是載波相位觀測值，ρ是衛星到測站之間的幾何距離，c是光速，dt是接收機鐘差，dT是衛星鐘差，dorb是衛星軌道誤差，dtrop是對流層延遲，dion是電離層延遲，λ是載波相位觀測值的波長，N是載波相位觀測值上的整周模糊度，dmult是多路徑誤差，ε是觀測噪聲。

為了消除接收機端的小數偏差，需要進行星間單差操作，公式為:

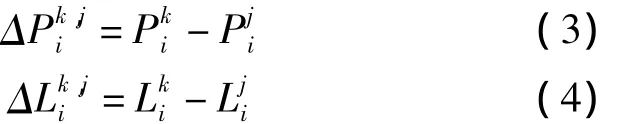
式中，k與j分別代表一顆GPS衛星，其中j代表參考衛星，并且滿足k≠j。

寬巷模糊度通過Melbourne-Wubbena組合觀測值［18－19］計算得到，計算公式為:

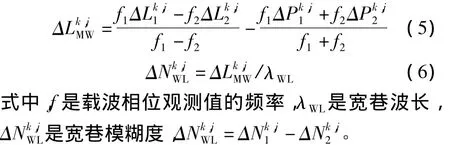
在固定寬巷模糊度之前，還需要進行衛星端寬巷模糊度小數偏差改正，來恢復寬巷模糊度的整數特性。CNES中心提供每日更新的衛星端寬巷模糊度小數偏差改正［9］，圖1顯示的是2012-11-30的32顆GPS衛星的衛星端寬巷模糊度小數偏差改正值。從圖中可知，個別衛星的寬巷模糊度小數偏差改正甚至達到1周，如果不進行改正，可能導致寬巷模糊度固定不準確。

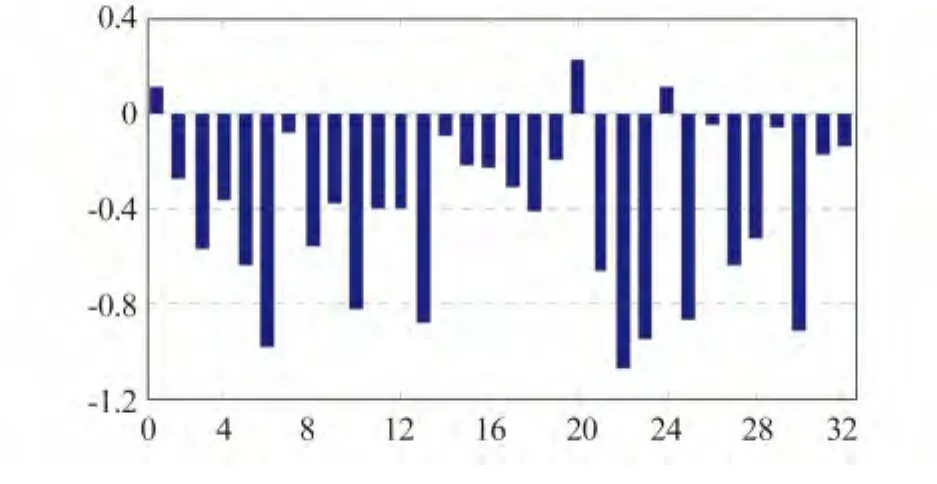
圖1 2012-11-30衛星端寬巷模糊度小數偏差改正Fig.1 Satellite FCB corrections of wide-lane ambiguities on November 30，2012

寬巷模糊度波長達0.86 m，可以直接通過取整運算來固定，但由于觀測噪聲較大，可能導致個別歷元的寬巷模糊度固定不準確，所以需要對其進行平滑來提高模糊度固定的準確率和可靠性。在進行平滑操作之前，還需進行周跳探測，若有周跳發生，必須從周跳發生的歷元重新進行平滑計算。本文使用TurboEdit方法［20］進行周跳探測。

1.3 窄巷模糊度固定

為了消除一階電離層誤差的影響，精密單點定位中通常使用消電離層組合觀測值，公式為:

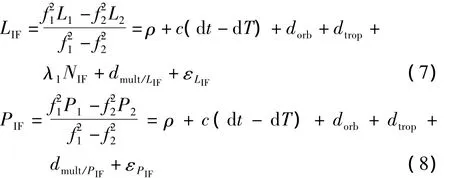
式中，NIF是消電離層模糊度，它可以分解成寬巷模糊度NWL與窄巷模糊度N1，其星間單差形式為:

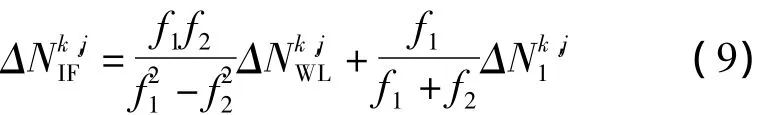
本文使用Kalman濾波進行解算，在寬巷模糊度固定成整數后，窄巷模糊度作為一個未知參數在Kalman濾波中進行估計。由于模糊度固定需要30～60 min［9，21］，所以對觀測時間少于 30 min 的衛星進行剔除。窄巷模糊度的固定方法同樣是直接取整。由于浮點模糊度在收斂前誤差較大，我們沒有對每個歷元直接固定，而是取觀測時段最后一個歷元的窄巷模糊度進行固定，以此來作為這顆衛星所有歷元的窄巷模糊度固定值。如果有周跳發生，則分段進行上述操作，因此該方法僅適用于精密單點定位事后處理。

由于窄巷模糊度的波長只有0.19 m，個別衛星的窄巷模糊度可能固定不準確。當窄巷模糊度固定不準確時，相當于引入粗差到觀測值中，所以必須進行質量控制來識別窄巷模糊度固定錯誤的衛星。質量控制的公式為:

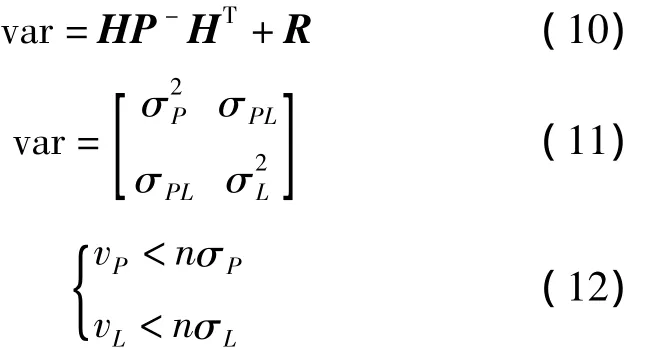
式中，H是系數陣，P－是預報的參數方差協方差陣，R是觀測值方差協方差陣，σP是測碼偽距改正值的中誤差，σL是載波相位改正值的中誤差，σPL是測碼偽距改正值與載波相位改正值的協方差，vP是測碼偽距觀測值與預報值之差，vL是載波相位觀測值與預報值之差，n是進行質量控制所取的倍數。n是經驗值，經驗證，n取8時效果較好。

當某顆衛星不滿足式(12)時，認為這顆衛星的窄巷模糊度固定不準確。這時，對這顆衛星的窄巷模糊度進行±2周內的搜索，找到vP與vL最小的窄巷模糊度。如果最小的 vP與 vL仍然不滿足式(12)，則剔除這顆衛星。

當窄巷模糊度固定成整數后，需要再一次進行Kalman濾波解算，此時寬巷模糊度和窄巷模糊度均為已知值，待估參數只有三維位置坐標和天頂對流層濕分量延遲。

現取2012-11-30 HERT站02:00～05:00的觀測數據對質量控制的重要性進行說明。圖2是進行質量控制與不進行質量控制兩種情況下星間單差PPP固定解的三維定位誤差對比。從圖2可知，若不進行質量控制，定位結果將出現嚴重的發散現象，說明個別衛星的窄巷模糊度固定不準確;而進行質量控制時，無發散情況出現，定位結果收斂到cm級。

2 結果與分析

選取 2012-11-30 HERT、LAMA、MATE、SOFI、WTZR、ZIM2 6個 IGS站02:00～05:00、05:00～08:00、08:00～11:00(GPS時)的觀測數據進行分析，數據采樣間隔30 s，截止高度角15°。

圖3為HERT站02:00～05:00觀測數據非差浮點解與星間單差固定解的定位誤差。從圖中可知，模糊度固定成整數后，東方向、北方向、高程方向的定位精度均有顯著提高。和非差浮點解相比，星間單差固定解具有更好的可靠性和穩定性。

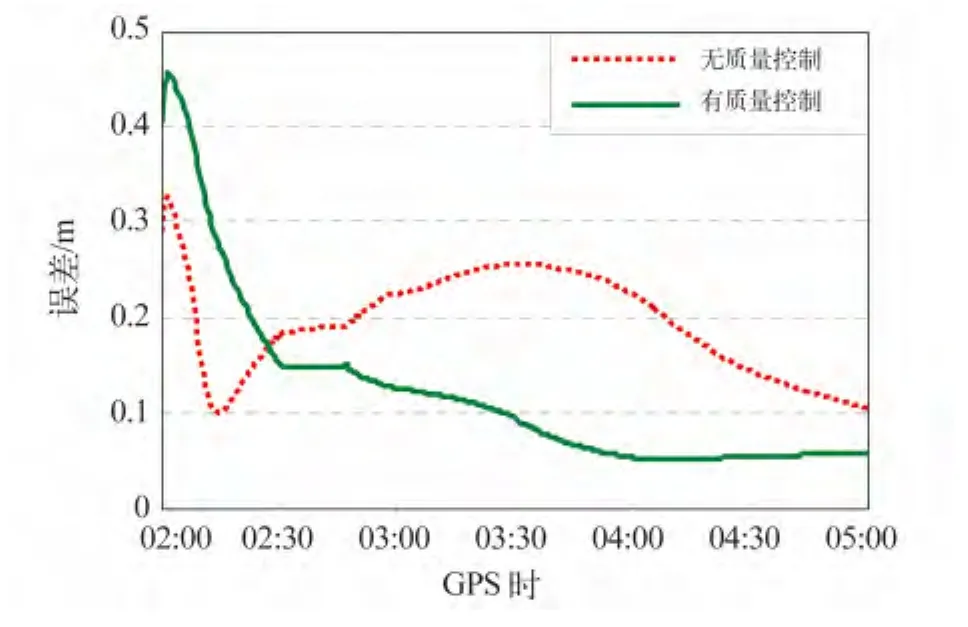
圖2 有無質量控制的星間單差PPP固定解三維定位誤差對比Fig.2 Comparison of 3-D position errors for PPP fixed resolution with and without quality control

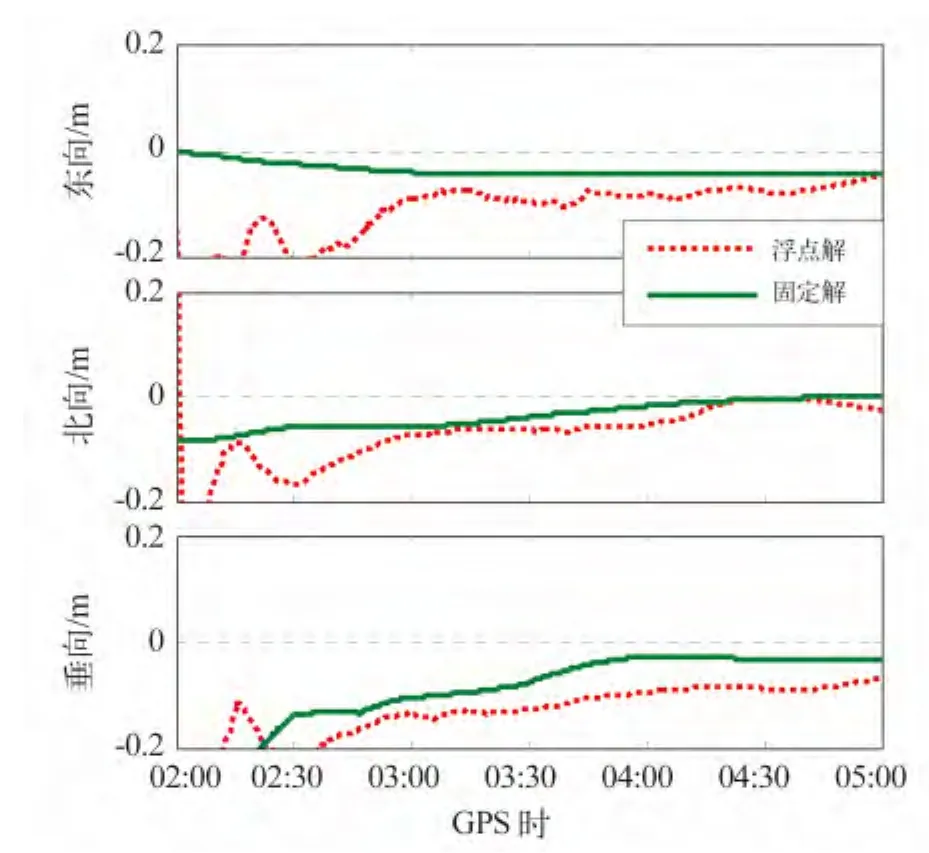
圖3 HERT站02:00～05:00觀測數據非差浮點解與星間單差固定解定位誤差對比Fig.3 Comparison of position errors with zero-difference PPP float resolution and with between-satellitedifference PPP fixed resolution using observation data from 2 to 5 at HERT

圖4為6個IGS站02:00～05:00觀測數據非差浮點解與星間單差固定解3個方向定位誤差的RMS統計值，統計時間是觀測時段最后20 min。從圖中可知，除SOFI站的高程方向與WTZR站的北方向之外，星間單差固定解的定位精度均有顯著提高。為了更加清楚地反映星間單差固定解相比非差浮點解定位精度的改善情況，表1給出了6個IGS站3個時段觀測數據的非差浮點解與星間單差固定解三維定位誤差的RMS統計值。從表中可知，模糊度固定之前，有5組觀測數據的三維定位誤差達到1 dm以上，而模糊度固定之后，三維定位誤差大幅降低，均在cm級。和非差浮點解相比，星間單差固定解三維定位精度的最大改善率達到63.8%。

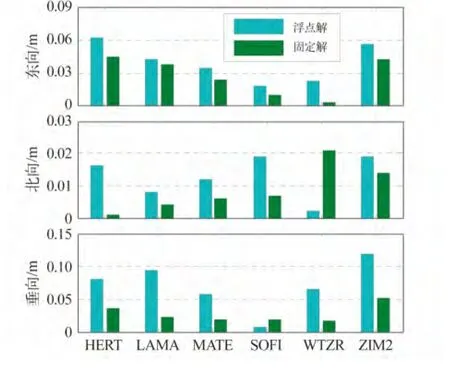
圖4 02:00～05:00觀測數據非差浮點解與星間單差固定解定位誤差的RMS比較Fig．4 RMS comparison of position errors with zero-difference PPP float resolution and with between-satellitedifference PPP fixed resolution from 2 to 5

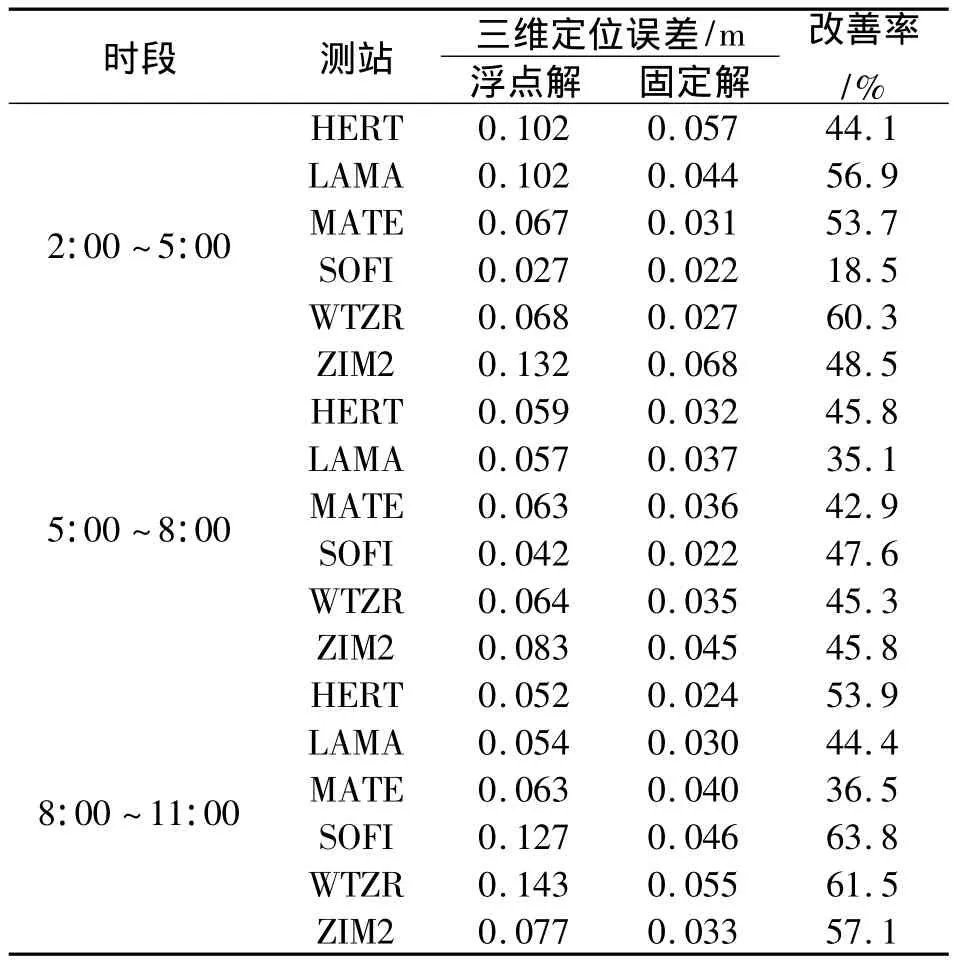
表1 非差浮點解與星間單差固定解三維定位誤差RMS比較Tab.1 RMS comparison of 3-D position errors with zerodifference PPP float resolution and with betweensatellite-difference PPP fixed resolution

3 結論

本文將消電離層模糊度分解成寬巷模糊度和窄巷模糊度，通過星間單差操作來移除接收機端的寬巷模糊度與窄巷模糊度小數偏差，然后利用IGS分析中心CNES提供的衛星端寬巷模糊度小數偏差值恢復寬巷模糊度的整數特性，而CNES提供的精密衛星鐘差數據在生成過程中吸收了衛星端的窄巷模糊度小數偏差，因此，應用其鐘差數據也可以恢復窄巷模糊度的整數特性。

利用6個IGS站提供的觀測數據進行分析，結果表明，模糊度固定成整數后，星間單差固定解和非差浮點解相比，定位精度有顯著改善，三維定位精度的最大改善率達到63.8%。

1 Zumberge J F.Precise point positioning for the efficient and robust analysis of GPS data from large networks［J］.Journal of Geophysical Research，1997，102(B3):5 005 －5 017.

2 Ge M.Resolution of GPS carrier-phase ambiguities in precise point positioning(PPP)with daily observations［J］.J Geod，2008，82(7):389 －399.

3 Geng J.Ambiguity resolution in precise point positioning with hourly data［J］.GPS Solution，2009，13(4):263 －270.

4 Geng J.Kinematic precise point positioning at remote marine platforms［J］.GPS Solution，2010，14(4):343 － 350.

5 Zhang X H，Li P，Guo F.Ambiguity resolution in precise point positioning with hourly data for global single receiver［J］.Advances in Space Research，2012，51(1):153 －161.

6 Li X X，Zhang X H.Improving the estimation of uncalibrated fractional phase offsets for PPP ambiguity resolution［J］.The Journal of Navigation，2012，65:513 －529.

7 Laurichesse D.Integer ambiguity resolution on undifferenced GPS phase measure-ments and its application to PPP and satellite precise orbit determination［J］.Navig J Inst Navig，2009，56(2):135 －149.

8 Collin P.Isolating and estimating undifferenced GPS integer ambiguities［C］.ION National Technical Meeting，San Diego，USA，2008.

9 Laurichesse D.The CNES real-time PPP with undifferenced integer ambiguity resolution demonstrator［C］.24th International Technical Meeting of the Satellite Division of the Institute of Navigation(ION GNSS 2011)，Portland，2011.

10 Kaplan E D，Hegarty C J.Understanding GPS principles and applications［M］.Artech House，2006.

11 Wielgosz P.Results of the application of tropospheric corrections from different troposphere models for precise GPS rapid static positioning［J］.Acta Geophysica，2012，60(4):1 236－1 257.

12 Niell A E.Global mapping functions for the atmosphere delay at radio wavelengths［J］.Journal of Geophysical Research，1996，101:3 227 －3 246.

13 Dach R.Bernese GPS software version 5.0 user manual［Z］.2007.

14 Abdel-salam M.Precise point positioning using un-differenced code and carrier phase observations［D］.University of Calgary，2005.

15 Kouba J，Héroux P.Precise point positioning using IGS orbit products［J］.GPS Solution，2000，5(2):12 －28.

16 Kouba J.A guide to using International GNSS Service(IGS)products［EB/OL］.http://igscb.jpl.nasa.gov/igscb/resource/pubs/UsingIGSProductsVer21.pdf，2009.

17 Urquhart L.Atmospheric pressure loading and its effects on precise point positioning［C］.22nd International Technical Meeting of the Satellite Division of the Institute of Navigation(ION GNSS 2009)，2001.

18 Melbourne W G.The case for ranging in GPS-based geodetic systems［C］.The First International Symposium on Precise Positioning with the Global Positioning System，Rockville，Maryland，USA，1985.

19 Wubbean G.Software developments for geodetic positioning with GPS using TI 4100 code and carrier measurements［C］.The First International Symposium on Precise Positioning with the Global Positioning System，Rockville，Maryland，USA，1985.

20 Geoffrey B.An automatic editing algorithm for GPS data［J］.Geophysical Research Letters，1990，17(3):199 －202.

21 Geng J.Towards PPP-RTK:Ambiguity resolution in realtime precise point positioning［J］.Advances in Space Research，2011，47:1 664 －1 673.

THE METHODS AND RESULTS OF PRECISE POINT POSITIONING WITH BETWEEN-SATELLITE-DIFFERENCE INTEGER AMBIGUITY FIXING

Pan Lin，Cai Changsheng and Zhu Jianjun
(School of Geosciences and Info-Physics，Central South University，Changsha 410083)

In the traditional precise point positioning(PPP)，the integer ambiguity can only be estimated as float value，which restricts the further enhance of PPP accuracy for the existence of fractional cycle biases(FCB)in the carrier phase observations from the receiver and satellite ends.In the study，the ionosphere-free ambiguity is decomposed into wide-lane(WL)and narrow-lane(NL)ambiguities.The between-satellite-difference(BSD)operation can remove the FCB included in WL and NL ambiguities at the receiver end.The satellite-based FCB contained in the WL ambiguity provided by the international GNSS service(IGS)analysis center CNES can be used to recover the integer nature of the WL ambiguity.Due to the precise satellite clock corrections provided by CNES assimilate the satellite-based FCB of the NL ambiguity，the integer nature of NL ambiguity can also be recovered after applying the precise clock corrections.The analysis results based on the IGS observation data indicate that the positioning accuracy of BSD PPP fixed resolution is significantly better than the zero-difference(ZD)PPP float resolution.The improvement rate of 3-dimensional positioning accuracy reaches 63.8%.

precise point positioning(PPP);integer ambiguity resolution;fractional cycle biases;wide-lane ambiguity;narrow-lane ambiguity

P228.4

A

1671-5942(2014)05-0090-04

2013-11-01

國家自然科學基金項目(41004011)。

潘林，男，1989年生，碩士研究生，主要研究方向為GNSS導航和精密單點定位。E－mail:panlin15116333665@163.com。