用移測顯微鏡測量平凸透鏡的基點

盧 杰，韓 力，曲延吉

（吉林大學物理學院，吉林長春 130012）

用移測顯微鏡測量平凸透鏡的基點

盧 杰，韓 力，曲延吉

（吉林大學物理學院，吉林長春 130012）

用干涉法測量平凸透鏡的曲率半徑，用視深法測量其折射率，通過基本公式計算得出透鏡的焦距和基點.

曲率半徑；折射率；視深度；基點

1 引 言

大學物理實驗中牛頓環實驗和基點測量實驗都是很典型、很基礎的實驗.大學物理中基點實驗一般用焦距儀測量透鏡的焦距和焦點位置，用節點儀測節點和主點的位置［1-2］.本文測量了透鏡的折射率和曲率半徑，通過基本公式求出焦距和基點［3-5］.通過基本公式的應用使學生清楚基點的概念的同時，更具體地把干涉應用到了實際測量中.

2 實驗原理

如圖1，厚透鏡L，其折射率為nL，第一折射面的曲率半R，第二折射面的曲率半R′，R′＝∞.透鏡的nL和R可以測量，即用nL和R來表述厚透鏡L的焦點、主點和節點的位置.

圖1 透鏡的焦點和主點位置

2.1 透鏡焦距

透鏡的光角度p，第一折射面的光焦度p1，第二折射面的光焦度p2，透鏡頂點距離t如圖1所示.

由于實驗考慮的對象R′＝∞，所以p2＝0，則

因為

則透鏡焦距為

2.2 主點距和節點距

如圖1，平行光Ⅰ進入透鏡后，通過第一折射面成像位置在F1′處，即第一表面的像方焦距光線通過第二表面再次成像到F′，那么由單球面成像公式及得：

如圖1，像方主點距

當平行光Ⅱ從第二表面入射時，第二表面不折射，則根據物像公式第一表面的像距就是焦距，物方主點距xH＝0，如圖1中H點.因為透鏡的物方和像方都在空氣中，因此節點和主點重合.

3 用移測顯微鏡測平凸透鏡的曲率半徑

3.1 實驗裝置

如圖2，平板玻璃P和凸透鏡L之間形成空氣楔，當鈉光燈（589.3 nm）垂直照時，通過移測顯微鏡可看見干涉圓環，環的疏密和級次取決于凸透鏡的曲率半徑.當看見干涉圓環時用測量牛頓環的方法測量凸透鏡的曲率半徑R.

圖2 用移測顯微鏡測曲率半徑

3.2 光程差的計算

在透鏡凸面與平面玻璃板之間形成空氣薄層如圖3所示.以波長為λ的單色光垂直照射到該裝置上，則由空氣薄層上、下表面反射的光波在P點發生干涉，所經歷的光程差Δ可以證明約為式中n是空氣薄層的折射率，d是考察點P處空氣層厚度，λ/2是光從疏媒質到密媒質交界面上C處反射時發生的半波損失.

圖3 薄膜表面干涉場

透鏡和玻璃方磚形成的空氣薄層等厚線是以接觸點為中心的同心圓，因此干涉圖像是以接觸點為中心的一族同心圓環，而且剛好接觸時中心是暗斑，對應某厚度的暗環，光程差Δ滿足：

整理得

3.3 曲率半徑的表達式

如圖4，設O點到P點的水平距離為rm，由圖4中幾何關系可知：

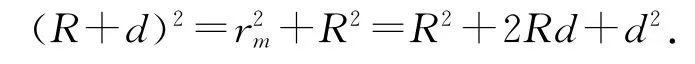
通常R比d大很多，略去d2項，則有

（10）式和（11）式聯立，其半徑rm為

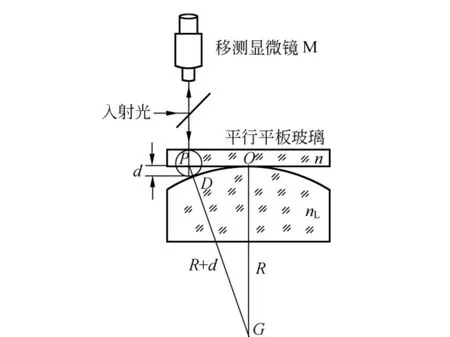
圖4 透鏡曲率半徑

（12）式表明，當λ和n已知時，只要測出第m級干涉暗環的半徑rm，就可算出透鏡的曲率半徑R.實驗中λ＝589.3 nm，空氣折射率n＝1.實際測量時為了減少誤差，把（12）式變形：（13）式表明，測量任意兩環的半徑和及半徑差，以及它們級次之差，通過式（13）可以算出透鏡曲率半徑R值.在實際測量中，如圖5所示，測量Lm2，Lm1和Lm1′的位置坐標，半徑和差直接測得.

圖5 干涉環讀數符號

4 用視深法測量凸透鏡的折射率

4.1 視深法測量折射率公式的推導

如圖6所示，在待測物質Ⅱ中深度為d處有一發光點Q，作QO垂直于界面.在介質Ⅰ中可以看到介質Ⅱ中Q點的虛像Q′，它是Q點發出經界面折射后光線的反向延長線與QO的交點.Q′點深度為h′稱為Q點的視深度（簡稱視深），視深h′的值決定于待測物質的折射率n.設光線由Q點發出，至M點發生折射，入射角和折射角分別為β和α，根據折射定律n1sinα＝n sinβ，如果介質Ⅰ是空氣，則n1＝1.h為實際深度.

圖6 視深法測折射率原理

上式表明，由Q點發出的不同方向的光線，折射后的延長線不再交于同一點，而與入射角β有關.但對于那些接近法線方向的光線，β≈0，sin2β≈0，cosβ≈1，可得

4.2 凸透鏡的折射率的測量方法

如圖7，把移測顯微鏡的半反鏡取下，在平臺上放坐標紙，移測顯微鏡清楚，在移測顯微鏡縱向標尺上讀數稱Q，然后在透鏡的中心用圓珠筆點上一個小點（稱痕跡），把凸透鏡放在移測顯微鏡上，痕跡在下方，調整移測顯微鏡看清楚痕跡，在移測顯微鏡縱向標尺上讀數稱Q1，把透鏡翻轉，即痕跡朝上，調整移測顯微鏡看清楚，再在移測顯微鏡縱向標尺上讀數稱Q2，完成1次測量.

圖7 視差法測量視深度示意圖

4.3 測量數據和結果

測量曲率半徑數據如表1所示，其中r＋表示半徑和，r－表示半徑差.

表1 測量曲率半徑數據mm

透鏡的曲率半徑

測量凸透鏡的折射率數據如表2所示，其中h＝Q2－Q，h′＝Q2－Q1.

表2 測量折射率數據 mm

透鏡的折射率為

透鏡的厚度為

透鏡焦距為

透鏡物方主點和節點距為透鏡像方主點和節點距為

5 結束語

由于本實驗是根據實驗室現有條件做的實驗，移測顯微鏡縱向讀數不夠精確，導致總的測量結果誤差比較大.如果開設學生實驗，可以改進移測顯微鏡縱向讀數精度，厚透鏡曲面的曲率半徑可再大一些，以提高測量精度.改進后加進牛頓環實驗中，可使牛頓環實驗［6-7］內容更充實.

［1］ 紀紅，韓力，王學風.普通物理實驗［M］.長春：吉林大學出版社，2009：158-162.

［2］ 曹琳敏，郭梓健，林柏婷，等.光具組基點測定實驗儀的設計［J］.湛江師范學院學報，2013，34（6）：50-52.

［3］ 趙凱華，鐘錫華.光學（上冊）［M］.北京：北京大學出版社，1982：16-82.

［4］ 姚啟均.光學教程［M］.北京：高等教育出版社，2009：130-200.

［5］ 玻恩M，沃爾夫E.光學原理（上冊）［M］.北京：科學出版社，1978.

［6］ 趙議魯.也談牛頓環實驗的誤差估算［J］.物理實驗，1995，15（6）：265-266.

［7］ 虞仲博，屠全良.牛頓環實驗等精度測量及其不確定度的評定與表示［J］.物理實驗，2000，20（5）：17-18.

［責任編輯：任德香］

Measuring the cardinal point of lens using a travelling microscope

LU Jie，HAN Li，QU Yan-ji
（College of Physics，Jilin University，Changchun 130012，China）

The radius of curvature of plano-convex lens was measured with interferometry.The refractive index of convex lens was measured with the method of apparent depth.The basic formula was used to calculate the focal length and the cardinal point.

radius of curvature；refractive index；apparent depth；cardinal point

O435

A

1005-4642（2014）10-0008-04

“第8屆全國高等學校物理實驗教學研討會”論文

2014-05-29；修改日期：2014-07-01

盧 杰（1958－），女，河北福寧人，吉林大學物理學院高級工程師，主要從事普通物理實驗教學工作.