布朗運動仿真實驗的設計與實現

丁望峰

（杭州師范大學理學院，浙江杭州 310036）

布朗運動仿真實驗的設計與實現

丁望峰

（杭州師范大學理學院，浙江杭州 310036）

介紹了布朗運動仿真實驗的設計與實現方法，利用“位置朗之萬方程”的數值離散化，最大程度還原真實的布朗運動.通過對仿真實驗數據的定量分析，并計算出了阿伏加德羅常量的近似值.

布朗運動；仿真實驗；阿伏加德羅常量

1 引 言

1827年，英國植物學家羅伯特·布朗（Robert Brown）在顯微鏡下觀察懸浮在水中的花粉時，發現花粉粒子會不停地進行連續不規則的運動.次年他以《植物花粉的顯微觀察》為題發表論文來描述這種運動，后來就以他的名字來命名這一現象［1］.由于當時人們的認識還沒有達到分子層面，一時產生了不少觀點.直到1905年前后愛因斯坦（Albert Einstein）發表了他有關布朗運動的論文，才第一次對這種不規則運動進行定量地分析.在他文章的最后，愛因斯坦還給出了驗證理論正確性的方法［2］：

這里對原文中的部分符號作了修改，其中N是阿伏加德羅常量，Δt是運動軌跡上鄰近2個記錄點的時間間隔，R是氣體常量，T是實驗溫度，η是實驗溫度下液體的黏度，a是球形微粒的半徑.在實驗上，每隔時間Δt記錄1次布朗顆粒的坐標，可以得到布朗運動的軌跡圖.通過測量顆粒在x方向上位移的平均平方值λ2x，就可以根據式（1）計算出阿伏加德羅常量的實驗測量值.

布朗運動實驗是對分子理論正確性很好的驗證，通過上面簡單的式子，就可以從布朗運動軌跡計算出阿伏加德羅常量的估算值，是一個很好的大學物理實驗項目.但目前相關教學實驗大都停留在定性的演示層面，要進行定量測量卻存在諸多困難［3，4］.首先，傳統的顯微鏡雖然能很好地觀測布朗運動，但卻無法精確記錄其運動軌跡，同時還存在尺度標定等問題.雖然一些實驗室已配備帶圖像采集系統的數字顯微鏡，但其價格不菲，不適合開展大規模教學.其次，由于不能確定哪些顆粒會進入視野，而對運動的顆粒進行尺寸測量非常困難，所以實驗所用的微粒小球尺寸需要精確訂制.另外，觀測區內一般會有多顆微粒，要想對1個顆粒進行追蹤，實驗操作上也有很大的難度.

為了解決以上難題，筆者設計了布朗運動的仿真實驗，能保證最大程度地還原真實的實驗條件和現象，加深學生對布朗運動的理解.整個仿真實驗采用Java語言開發，同時提供Java應用程序和Java Applet兩種版本，后者可以嵌入網頁供學生遠程操作.

2 實驗原理

布朗運動的模擬通過求解朗之萬方程（Langevin equation）來實現［5，6］：

其中η是液體黏度.

根據隨機耗散理論，隨機作用項Ri（t）與摩擦系數滿足如下關系

在實際模擬中，往往假定隨機作用力在不同時刻是不相關的，即式（5）可采用如下形式

式（6）把布朗粒子受到的隨機熱擾動與體系溫度及摩擦系數關聯起來.

當液體的黏滯阻力相對于布朗粒子而言很大時，布朗粒子看上去像沒有慣性質量一樣地運動，這時式（2）等號右邊可近似為零，即

該等式也被稱為“位置朗之萬方程”，是朗之萬方程的“過阻尼”形式［6］.利用式（7）進行的動力學模擬稱為布朗動力學（Brownian dynamics）.

仿真實驗是基于式（7）的數值離散化來完成的.計算機數值化模擬把連續的真實的物理過程分割成時間間隔為Δt的狀態點，通過計算從t時刻到t＋Δt時刻狀態點的演化來實現模擬.這里記位矢ri的三維坐標為（x1，x2，x3），則再根據式（7），xα（α＝1，2，3）方向上粒子i從t到t＋Δt的演化方程為

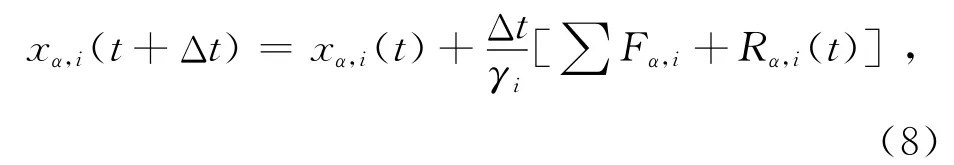
從上式可以看出，位置朗之萬方程中并不出現速度，粒子下一步的走向完全取決于粒子此刻受到的明確作用力和熱擾動產生的隨機作用力.由于本文中的布朗運動不考慮顆粒之間的相互作用，即∑Fα，i為零，上式可簡化為

為了滿足式（3）和式（4）要求，隨機作用力Rα，i（t）可以取期望值為0、標準差為的高斯分布，記為

從式（9）和（10）可以看到，位置朗之萬方程的具體實現已與顆粒的材質沒有關系，而這正是布朗運動的特征之一.

3 實驗設計

如圖1所示，仿真實驗界面分為實驗觀測區與實驗參量控制區.左邊的觀測區是對布朗運動軌跡的顯微放大，通過下面的倍率選擇按鈕可以選擇不同的放大倍數.右邊的參量控制區為實驗提供了豐富的選項，實驗者可以選取不同的實驗參量，對布朗運動的諸多特性進行定性比較和定量分析，比如不同顆粒大小、密度，液體溫度、黏度等對布朗運動的影響.如果只是觀測實驗現象，還可以設定較多的粒子數，不同的顆粒軌跡會用不同的顏色表示.當實驗者設定好所有參量，就可以點擊“開始”按鈕開始實驗，顆粒在觀測區內的連續運動軌跡用曲線表示，設定時間間隔所記錄的點用圓點表示.程序內部的模擬時鐘與電腦時鐘同步，如果選擇每隔10 s記錄1個點，那么記錄30個點就需要300 s的時間.如果顆粒運動不明顯或者越出了視野，可以實時地調節放大倍數，以達到最佳的觀測效果.當記錄了所需的足夠點后，選擇停止并保存軌跡，所記錄的點的坐標就會輸出到文件.值得注意的是，保存的軌跡只是點的坐標，而并非實驗過程中觀測到的連續的曲線.

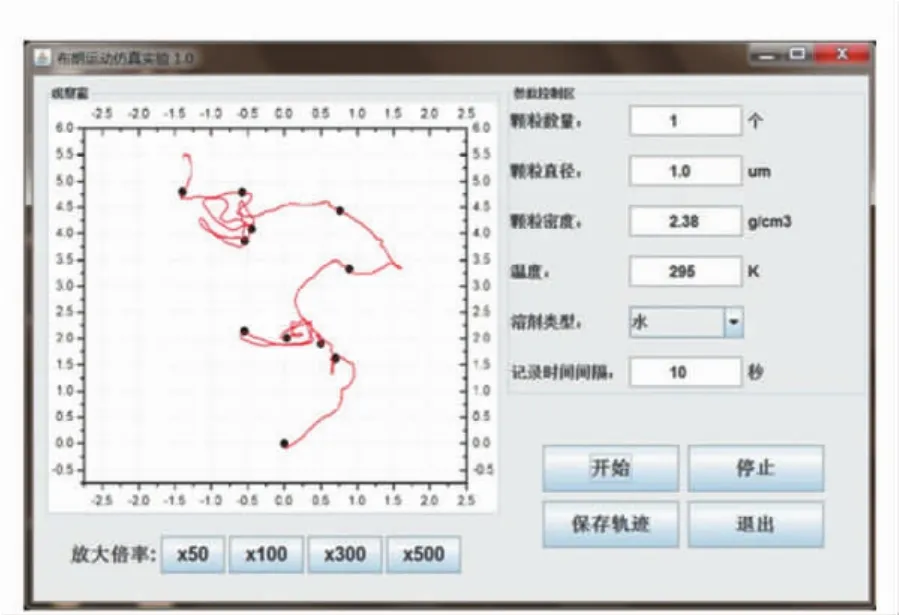
圖1 布朗運動仿真實驗界面

4 實驗結果與分析

首先，做定性的分析.通過參量的調節，可以驗證布朗運動的如下特性：

1）粒子運動永不停止，沒有固定的軌跡；

2）運動隨溫度的升高而加劇；

3）運動速度與粒子大小成反正；

4）溶液的黏度減小時，布朗運動加劇；

5）粒子的成分或密度不會影響粒子的運動.

接下來，用愛因斯坦給出的式（1）進行定量分析.這里考慮直徑1μm的SiO2顆粒在溫度為295 K的水中的布朗運動，模擬的相關參量如下：直徑為1.0μm，密度為2.38 g/cm3，溫度為295.0 K，水的黏度為1.003 g/（m·s），時間步長為10 s。

圖2中相鄰兩點的記錄時間間隔為10 s，共記錄了30個點.計算兩點間的距離平方

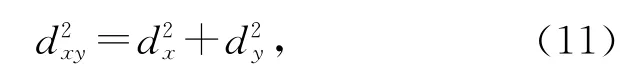
一共可得到29個數據，對其求平均

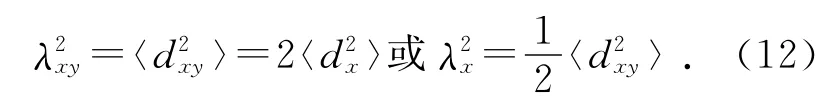
從計算結果來看，僅從少量的坐標數據就可以得到較為精確的阿伏加德羅常量值.

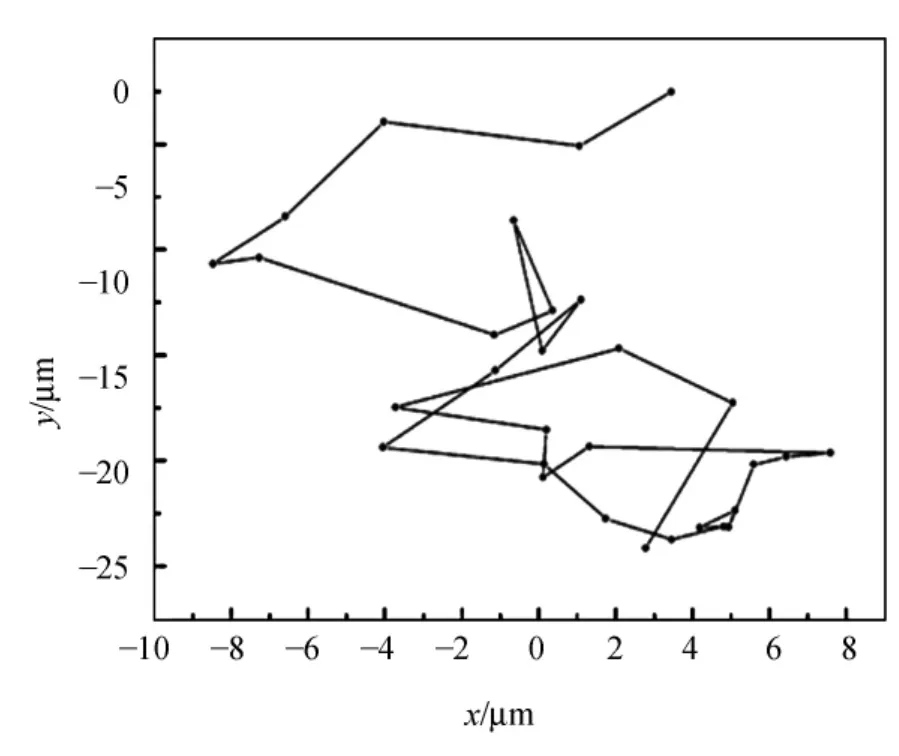
圖2 直徑為1μm的SiO2微粒在295 K的水中做布朗運動的軌跡

表1 對圖2中的布朗運動軌跡的數值分析

5 結束語

本文介紹了布朗運動仿真實驗原理，并據此設計開發出適合學生操作的仿真實驗.模擬程序通過參量的調節，不僅能定性地展示布朗運動的特點，而且可以對布朗運動的軌跡進行定量分析，計算出較為精確的阿伏加德羅常量值，由此也驗證了計算機仿真是對物理運動規律的真實反映.

［1］ 郝柏林.布朗運動理論一百年［J］.物理，2011，40（1）：1-7.

［2］ Einstein A.Investigations on the thoery of the Brownian movement［M］.New York：Dover，1956.

［3］ 李鴻寅.介紹布朗運動的一種演示實驗 ［J］.物理實驗，1981，1（1）：23-24.

［4］ 梁超聯.用顯微鏡觀察氣體中的布朗運動［J］.物理實驗，2000，20（8）：34.

［5］ 王子瑜，曹恒光.布朗運動、朗之萬方程式、與布朗動力學［J］.物理，2005，27（3）：456-461.

［6］ Coffey W T，Kalmykov Yu P，Waldron J T.The Langevin Equation［M］.Second Edition.Singapore：World Scientific，2004.

［責任編輯：郭 偉］

Simulation experiment of Brownian motion

DING Wang-feng
（College of Science，Hangzhou Normal University，Hangzhou 310036，China）

The design and implement method of Brownian motion simulation experiment were introduced.The characteristics of real Brownian motion was maximally retained by the numerial discretization of position of Langevin equation.By quantitative analyzing of the motion traces，a close approximation of Avogadro constant was obtained.

Brownian motion；simulation experiment；Avogadro constant

O414.2；O4-39

A

1005-4642（2014）10-0038-03

2014-05-16；修改日期：2014-08-25

丁望峰（1984－），男，浙江義烏人，杭州師范大學理學院實驗師，博士，主要從事實驗物理方面教學工作.