考慮河流沖刷作用的車(chē)橋耦合系統(tǒng)動(dòng)力分析

李克冰，張 楠，方翔宇，田 園，夏 禾

（北京交通大學(xué) 土木建筑工程學(xué)院，北京 100044）

隨著我國(guó)經(jīng)濟(jì)的發(fā)展，跨江大橋、超長(zhǎng)跨海灣大橋的建設(shè)已經(jīng)進(jìn)入一個(gè)飛速發(fā)展的階段。目前，高速鐵路大規(guī)模興建，其中高架橋梁的總里程占線路總長(zhǎng)的比例非常高，這些橋梁中跨江跨海的也不在少數(shù)。許多橋梁不同程度地受到水流沖刷的影響。近年來(lái)出現(xiàn)一些因沖刷使橋梁發(fā)生倒塌的事故，給生命財(cái)產(chǎn)安全造成危害。2001年8月，藍(lán)煙線外夾河橋和東萊線東泉河橋分別因橋渡沖刷而倒塌，因及時(shí)攔停了列車(chē)，未造成重大人員財(cái)產(chǎn)損失；2002年6月，西安灞河爆發(fā)洪水，將隴海線灞河橋1～5號(hào)橋墩沖垮，1～6孔梁墜落，造成隴海線雙線中斷行車(chē)14．5小時(shí)；2008年9月份，臺(tái)灣南橫公路高雄縣甲仙鄉(xiāng)甲仙大橋被湍急的旗山溪水沖擊，橋墩松動(dòng)，橋面陷落，無(wú)法通行而封橋。

水流沖刷對(duì)基礎(chǔ)埋深的改變直接會(huì)對(duì)橋梁動(dòng)力特性以及運(yùn)行在橋上的列車(chē)的動(dòng)力響應(yīng)產(chǎn)生影響。因此，對(duì)在河流沖刷作用下的車(chē)橋系統(tǒng)動(dòng)力響應(yīng)及列車(chē)行車(chē)安全性的分析研究是必要的。

在進(jìn)行河流沖刷對(duì)橋梁動(dòng)力響應(yīng)的影響研究時(shí)，首先要確定沖刷深度。目前，橋墩沖刷深度的計(jì)算主要有三類(lèi)：基于沖深與來(lái)流強(qiáng)度關(guān)系的來(lái)流相關(guān)法，基于橋墩沖刷深度主要影響參數(shù)進(jìn)行量綱分析的經(jīng)驗(yàn)方法，還有解析法或者半經(jīng)驗(yàn)法［1］。從國(guó)內(nèi)外現(xiàn)行的沖刷深度計(jì)算公式看都是經(jīng)驗(yàn)性的或半經(jīng)驗(yàn)性的，目前尚未發(fā)現(xiàn)純理論推導(dǎo)公式，大都采用實(shí)驗(yàn)資料來(lái)建立局部深度的關(guān)系式，然后用野外實(shí)橋觀測(cè)資料來(lái)修正系數(shù)和指數(shù)得到?jīng)_刷深度計(jì)算公式［2］。

本文僅考慮沖刷作用對(duì)橋梁基礎(chǔ)剛度的影響，并認(rèn)為此類(lèi)影響仍在線性范圍內(nèi)，因此有關(guān)車(chē)橋動(dòng)力分析仍可以通用的方式進(jìn)行。吳定俊等［3］以m法確定了基礎(chǔ)彈性剛度，建立了考慮樁土相互作用的高速鐵路橋梁－墩－基礎(chǔ)體系列車(chē)過(guò)橋動(dòng)力分析模型；蔣通等［4］將支架及支架下的樁基礎(chǔ)和土體的彈性變形采用彈性支座模擬，研究了彈性支撐條件下對(duì)車(chē)－橋體系振動(dòng)的影響；單德山等［5］以某鐵路曲線多跨簡(jiǎn)支梁橋?yàn)槔瑢鐾羺^(qū)地面以下的地基土等效為線性彈簧，從而簡(jiǎn)單的考慮了樁土的相互作用效應(yīng)；李小珍等［6］以等效地基剛度考慮橋梁樁土相互作用，分析了某主跨為1 120m的懸索橋的車(chē)橋動(dòng)力性能。

河流沖刷可顯著降低高速鐵路橋梁基礎(chǔ)埋深，有可能影響橋梁整體剛度，劣化其服役性能。因此本文進(jìn)行了群樁基礎(chǔ)的沖刷深度計(jì)算，建立了基于全過(guò)程迭代的列車(chē)－橋梁系統(tǒng)動(dòng)力分析模型，通過(guò)考慮河流沖刷引起的群樁基礎(chǔ)等效剛度變化，進(jìn)行水流沖刷對(duì)車(chē)橋動(dòng)力響應(yīng)及行車(chē)安全性的影響研究。

1 樁基承臺(tái)基礎(chǔ)沖刷深度

對(duì)于架設(shè)橋梁的河道，除河床的自然演變外，還有橋梁孔徑壓縮水流和墩臺(tái)阻擋水流引起的沖刷，各種沖刷交織在一起同時(shí)進(jìn)行，沖刷過(guò)程較為復(fù)雜。根據(jù)泥沙運(yùn)動(dòng)和河床變形原理，橋墩附近的河床變形的原因可以分為三類(lèi)：河道自然演變引起的河床變形，一般沖刷和局部沖刷。目前對(duì)沖刷深度的計(jì)算，一般先算出一般沖刷，再用一般沖刷后的水流條件計(jì)算局部沖刷，二者相加即為總沖刷深度。

總體來(lái)說(shuō)，國(guó)內(nèi)外對(duì)群樁基礎(chǔ)局部沖刷的預(yù)測(cè)，目前尚屬于初級(jí)階段［7］。

國(guó)外眾多學(xué)者對(duì)群樁橋墩局部沖刷做了大量的研究和實(shí)踐工作。國(guó)際水力學(xué)協(xié)會(huì)組織國(guó)際專(zhuān)家編著出版一系列文件和手冊(cè)，主要描述了影響樁群沖刷的機(jī)理，同時(shí)對(duì)雙樁柱橋墩的局部沖刷特性進(jìn)行了試驗(yàn)研究，提出了雙圓柱體的樁群系數(shù)Kgγ，但未能給出計(jì)算公式；美國(guó)聯(lián)邦公路局發(fā)布的行業(yè)規(guī)范，針對(duì)簡(jiǎn)單布設(shè)群樁的橋基在單向水流作用下的局部沖刷推薦了計(jì)算公式，用群樁相連的等效實(shí)體樁乘以群樁的間距校正系數(shù)來(lái)計(jì)算局部沖刷深度，即：式中：S為樁中心的間距；Φ為樁的直徑；Ks為間距校正系數(shù)；Ka為迎流角校正系數(shù)；hb為等效實(shí)體樁的最大局部沖刷深度；a為墩寬；k2為水流沖擊角系數(shù)；k3為河床狀態(tài)系數(shù)；k4為床沙粒徑系數(shù)；hp為一般沖刷后的水深；Fr為弗勞德數(shù)。

我國(guó)鐵路和公路系統(tǒng)廣泛協(xié)作，對(duì)非粘性河質(zhì)橋墩局部沖刷進(jìn)行了研究。對(duì)于群樁橋基的局部沖刷，我國(guó)行業(yè)規(guī)范采用“墩形系數(shù)法”進(jìn)行預(yù)測(cè)計(jì)算，以一個(gè)單樁作為參照物，采用樁群系數(shù)計(jì)入樁群的影響來(lái)計(jì)算局部沖刷深度，這里樁群系數(shù)的物理意義相當(dāng)于墩形系數(shù)。

我國(guó)鐵路規(guī)范［8］中非粘性土河床的局部沖刷深度計(jì)算公式為：

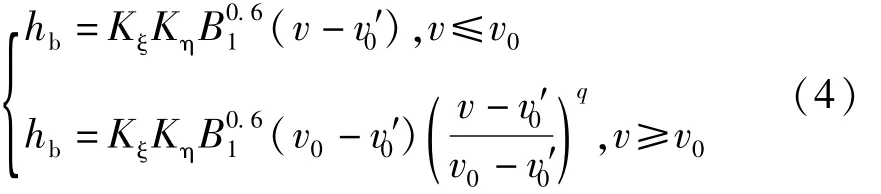
對(duì)于樁基承臺(tái)橋墩，當(dāng)承臺(tái)地面高于水面時(shí)引進(jìn)樁群系數(shù) Km，代入公式（4）計(jì)算：

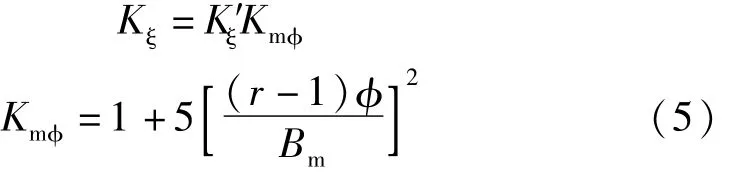
式中：hb為橋墩局部沖刷深度；Kη為河床顆粒影響系數(shù)；v為墩前水流行近流速；B1為橋墩計(jì)算寬度；v0為河床泥沙起動(dòng)流速；v′0為墩前始沖流速；Kξ為墩形系數(shù)；K′ξ為單樁形狀系數(shù)；Bm為樁群垂直水流的分布寬度；r為樁的排數(shù)；為樁徑；q為指數(shù)。

當(dāng)承臺(tái)底面相對(duì)高度在0≤h／h≤1．0時(shí)，沖刷深度hb按下式計(jì)算：

式中：h為承臺(tái)底到河床的距離；K為淹沒(méi)樁體折減系數(shù)，；K、B按承臺(tái)底處于ξ11一般沖刷線計(jì)算；Kh2為墩身承臺(tái)減少系數(shù)。

為了獲得整體的沖刷深度，還需要計(jì)算橋位處的一般沖刷深度，我國(guó)鐵路規(guī)范［8］中對(duì)非粘性土河床的一般沖刷深度計(jì)算公式為：

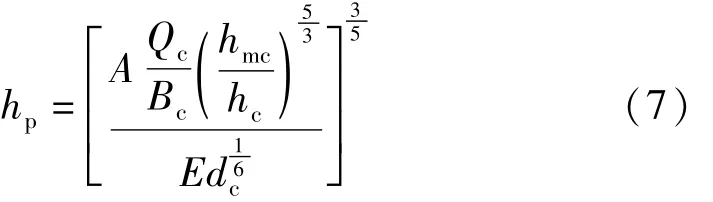
式中：hp為橋下一般沖刷后的最大水深；hmc為橋下河槽部分的最大水深；hc為橋下河槽部分的平均水深；Bc為橋下河槽部分橋孔過(guò)水凈寬；Qc為橋下河槽部分通過(guò)的設(shè)計(jì)流量；E為與汛期含沙量有關(guān)的系數(shù)；A為單寬流量集中系數(shù)；dc為河槽平均粒徑，以mm為單位。

2 群樁基礎(chǔ)等效剛度

當(dāng)橋墩周?chē)l(fā)生局部沖刷，基礎(chǔ)埋深減小，引起橋墩墩身及上部結(jié)構(gòu)的一系列變化，需要我們對(duì)其剛度進(jìn)行重新驗(yàn)算。建立橋梁有限元模型時(shí)采用等效剛度模型，等效剛度模型就是承臺(tái)處施加6個(gè)自由度的彈性約束，將樁基礎(chǔ)的剛度簡(jiǎn)化到承臺(tái)處，模擬樁基和土體對(duì)上部結(jié)構(gòu)的影響。

根據(jù)文獻(xiàn)［9］采用地基系數(shù)法，即m法，計(jì)算土的彈性抗力，將土視為具有隨深度成正比增長(zhǎng)的地基系數(shù)的彈性變形介質(zhì)，深度y處垂直于基礎(chǔ)側(cè)面的水平地基系數(shù)Cy＝my，深度h處基底豎向地基系數(shù)C0＝m0h，m、m0為地基系數(shù)的比例系數(shù)。對(duì)于群樁基礎(chǔ)，以構(gòu)件相互影響系數(shù)k計(jì)入多構(gòu)件對(duì)土的彈性抗力的影響。

定義樁群的剛度系數(shù)δAB為當(dāng)承臺(tái)發(fā)生單位B種變位時(shí)，所有樁頂（必要時(shí)包括承臺(tái)側(cè)面）引起的A種反力之和。忽略樁頂橫向位移與轉(zhuǎn)角的耦合關(guān)系，計(jì)算群樁基礎(chǔ)的等效剛度可得到順橋向平移剛度δaa1、橫橋向平移剛度δaa2、豎向平移剛度δaa3和順橋向抗扭剛度 δcc1、橫橋向抗扭剛度 δcc2、豎向抗扭剛度 δcc3，如圖1所示。

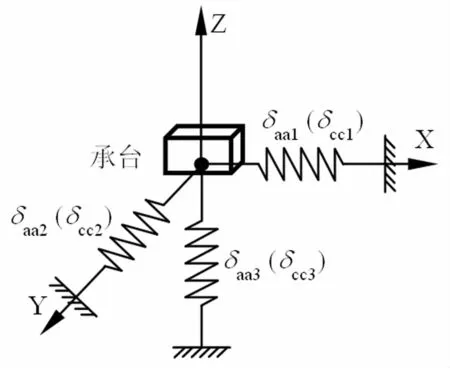
圖1 群樁等效剛度示意圖Fig．1 Schematic diagram of equivalent-stiffness model

計(jì)算得到的群樁基礎(chǔ)等效剛度可以表述為以下矩陣形式：

3 基于全過(guò)程迭代的車(chē)橋系統(tǒng)動(dòng)力分析

列車(chē)－橋梁動(dòng)力耦合系統(tǒng)可分為列車(chē)子系統(tǒng)和橋梁子系統(tǒng)兩部分，兩者通過(guò)輪軌關(guān)系相聯(lián)系，系統(tǒng)的激勵(lì)源為軌道不平順。

3.1 列車(chē)子系統(tǒng)

列車(chē)子系統(tǒng)模型由多節(jié)車(chē)輛組成。每節(jié)車(chē)輛模型都是由一個(gè)車(chē)體、兩個(gè)轉(zhuǎn)向架和四個(gè)輪對(duì)組成的多自由度體系，如圖2所示。

將車(chē)體、轉(zhuǎn)向架和輪對(duì)均視為剛體，忽略其在振動(dòng)中的彈性變形。假定每個(gè)車(chē)體和轉(zhuǎn)向架擁有橫擺y、沉浮z、側(cè)滾rx、點(diǎn)頭ry和搖頭rz共5個(gè)自由度，每個(gè)輪對(duì)有橫擺、側(cè)滾、沉浮共3個(gè)自由度，即每節(jié)車(chē)輛有27個(gè)自由度。忽略列車(chē)各節(jié)車(chē)輛之間的連接，不同車(chē)輛之間的振動(dòng)不存在耦合關(guān)系，可以分別求解各節(jié)車(chē)輛的運(yùn)動(dòng)狀態(tài)和輪軌力。

單節(jié)車(chē)輛的運(yùn)動(dòng)方程可以由下式表示：

式中：MV、CV、KV、XV分別是單節(jié)車(chē)輛的質(zhì)量矩陣、阻尼矩陣、剛度矩陣以及單節(jié)車(chē)輛的位移向量；PV是作用在單節(jié)車(chē)輛上的外加力向量。車(chē)輛系統(tǒng)方程的建立方法參考文獻(xiàn)［10－15］。

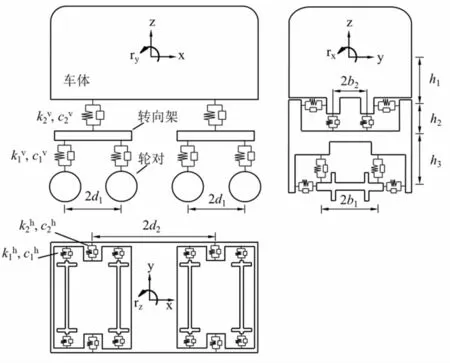
圖2 車(chē)輛動(dòng)力分析模型Fig．2 Dynamic model of vehicle system

3.2 橋梁子系統(tǒng)

橋梁子系統(tǒng)方程可以表示為

式中：Mb、Kb分別為橋梁子系統(tǒng)的質(zhì)量矩陣和剛度矩陣，可由有限元法求得；Cb為橋梁子系統(tǒng)的阻尼矩陣，可由各類(lèi)比例阻尼法求得；Xb為橋梁子系統(tǒng)的位移向量；Fb為作用在橋梁子系統(tǒng)的力向量，即輪軌間作用力，由下述的輪軌關(guān)系假定得到。

3．3 輪軌關(guān)系

輪軌間作用力作用于左右輪軌接觸點(diǎn)。假定在豎向上輪對(duì)與鋼軌密貼，輪軌間豎向作用力為常數(shù)，其值為一系懸掛力、輪對(duì)慣性力、靜軸重三者之和。同時(shí)假定輪軌關(guān)系在橫向上滿足Kalker蠕滑理論，并且車(chē)輪與軌道間相對(duì)運(yùn)動(dòng)與其接觸力之間符合線性關(guān)系。由文獻(xiàn)［16］假定，橫向蠕滑系數(shù)為常數(shù)，輪軌間橫向作用力為蠕滑系數(shù)與輪軌橫向運(yùn)動(dòng)速度的乘積，因此認(rèn)為橫向輪軌相互作用力與輪軌橫向相對(duì)速度成正比。將式（8）右端項(xiàng)中車(chē)輛的速度項(xiàng)移至左端，即為

式中：CC為由于輪軌間蠕滑產(chǎn)生的附加阻尼矩陣。

3．4 全過(guò)程迭代法求解系統(tǒng)方程

將列車(chē)子系統(tǒng)方程和橋梁子系統(tǒng)方程聯(lián)立，并設(shè)列車(chē)的節(jié)數(shù)為n，可得到車(chē)－橋耦合系統(tǒng)的動(dòng)力方程為

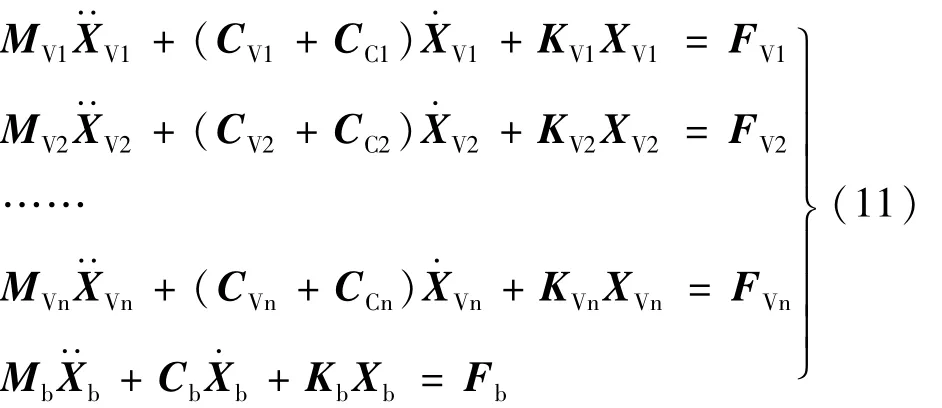
式（11）中，前n行為列車(chē)子系統(tǒng)方程，后1行為橋梁子系統(tǒng)方程。本文采用全過(guò)程迭代法［17］求解系統(tǒng)方程，首先假定橋梁子系統(tǒng)為剛性，求解獨(dú)立的列車(chē)子系統(tǒng)方程，得到列車(chē)動(dòng)力響應(yīng)及輪軌間作用力時(shí)程，然后將輪軌間作用力施加于橋梁，求解獨(dú)立的橋梁系統(tǒng)方程而得到橋梁的動(dòng)力響應(yīng)，將求出的橋面動(dòng)力響應(yīng)時(shí)程與軌道不平順疊加作為新的車(chē)輛系統(tǒng)激勵(lì)進(jìn)行下一步迭代。其計(jì)算過(guò)程見(jiàn)圖3。

圖3 全過(guò)程迭代計(jì)算過(guò)程Fig．3 Inter-system iteration process

由于在迭代過(guò)程中單獨(dú)求解橋梁子系統(tǒng)方程，因此對(duì)于復(fù)雜或直接計(jì)算系統(tǒng)動(dòng)力矩陣?yán)щy的橋梁，可利用通用有限元軟件直接計(jì)算其在輪軌力時(shí)程作用下的動(dòng)力響應(yīng)，以代替建立和求解式（9）。

全過(guò)程迭代法每步計(jì)算即為全時(shí)程計(jì)算，而非針對(duì)單一時(shí)間步的計(jì)算。因此，每次列車(chē)或橋梁子系統(tǒng)的求解，分別得到列車(chē)或橋梁子系統(tǒng)全部計(jì)算時(shí)間內(nèi)的響應(yīng)過(guò)程，而非某一時(shí)刻的響應(yīng)。

4 算 例

某跨江特大橋橋址區(qū)與河道呈垂直相交，橋墩基礎(chǔ)采用樁基承臺(tái)基礎(chǔ)。橋梁2＃～5＃墩之間為（32＋48＋32）m的單線連續(xù)梁，5＃～9＃墩之間的梁為單線32 m簡(jiǎn)支梁，9＃～12＃墩之間為（40＋64＋40）m的單線連續(xù)梁，橋梁截面如圖4～圖6所示。橋墩之中4＃～10＃墩位于江上，受河流沖刷影響，墩高7～12．1 m。橋位所在位置河床寬約243 m，橋址處設(shè)計(jì)控制的水文數(shù)據(jù)為：設(shè)計(jì)流量 Q＝5 500 m3／s，設(shè)計(jì)水位 H＝240．95 m，河面寬度約256 m，平均水深約6．13 m，最大水深為7．02 m。據(jù)勘察揭露顯示，橋址區(qū)地表層為粗砂、圓礫土等，下伏氣孔狀玄武巖，抗壓強(qiáng)度為44．5 MPa。

圖4 32＋48＋32 m連續(xù)梁截面圖（單位：mm）Fig．4 Section of continuous beam with spans（32＋48＋32）m（Unit：mm）

圖5 40＋64＋40 m連續(xù)梁截面圖（單位：mm）Fig．5 Section of continuous beam with spans（40＋64＋40）m（Unit：mm）

圖6 32 m簡(jiǎn)支梁截面圖（單位：mm）Fig．6 Section of 32 m span simply supported beam（Unit：mm）

本文采用有限元軟件MIDAS建立該橋2＃～12＃墩之間橋跨的有限元模型，如圖7所示。模型中以空間梁?jiǎn)卧M墩梁，以主從節(jié)點(diǎn)模擬支座，以節(jié)點(diǎn)彈性支承模擬基礎(chǔ)等對(duì)上部結(jié)構(gòu)的影響，承臺(tái)基底彈性約束的剛度按表4中取值，將橋梁二期恒載以提高材料密度的方法施加于梁體。

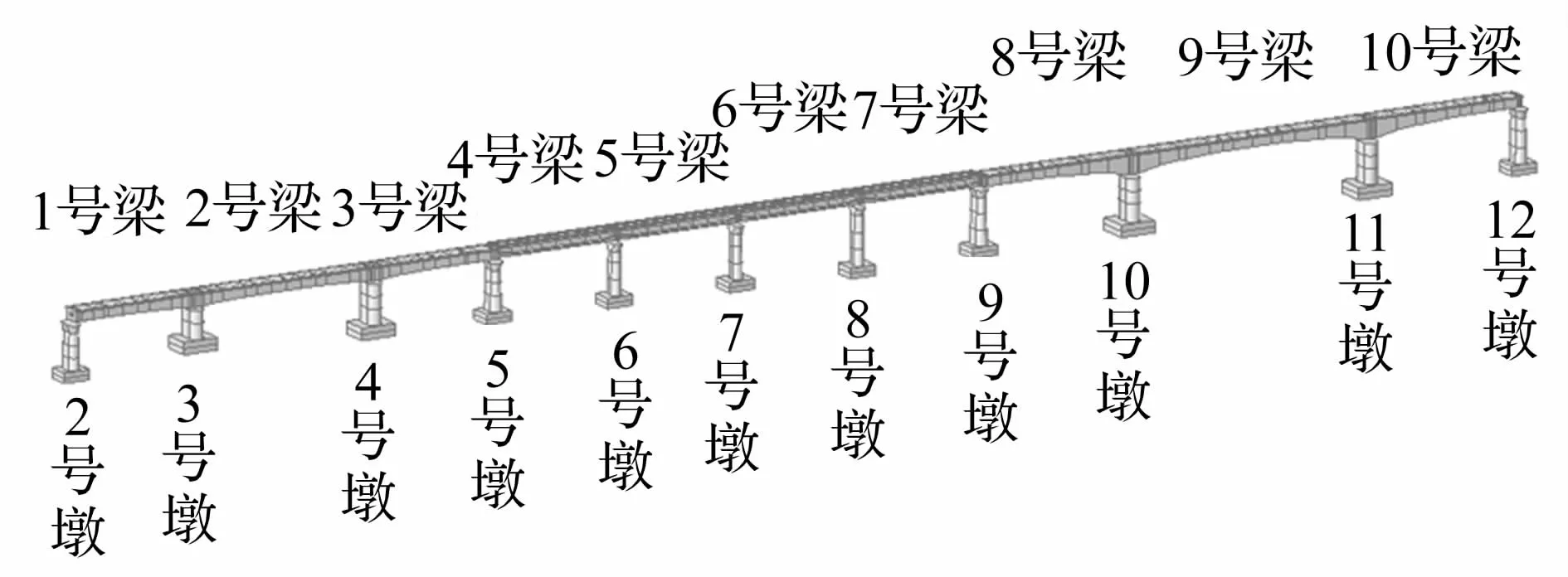
圖7 橋梁有限元模型Fig．7 FE model of bridge

4．1 沖刷深度與等效剛度

結(jié)合實(shí)際的水文資料并根據(jù)式（7）計(jì)算得到一般沖刷深度，見(jiàn)表1。偏安全考慮，河道平均深度增大2．03 m。一般沖刷前后各墩承臺(tái)埋深如表2中所示，負(fù)號(hào)表示橋墩在受到一般沖刷之后承臺(tái)底面均高于一般沖刷線。

表1 一般沖刷計(jì)算參數(shù)及沖刷深度Tab．1 Calculation parameters and general scouring depth

表2 一般沖刷前后各墩承臺(tái)埋深Tab．2 Buried depth of pile-caps pre and post general scouring

在計(jì)算局部沖刷深度時(shí)，4＃墩與10＃墩承臺(tái)底面低于一般沖刷線，按上部實(shí)體進(jìn)行計(jì)算，即按公式（4）計(jì)算；其它各墩按公式（6）計(jì)算。計(jì)算得到各墩局部沖刷深度見(jiàn)表3。局部沖刷之后，全部橋墩承臺(tái)底面均高于沖刷線，并且樁身暴露相當(dāng)長(zhǎng)度。8＃墩沖刷前后如圖8所示。

表3 各墩局部沖刷深度Tab．3 Local scouring depth of all piers

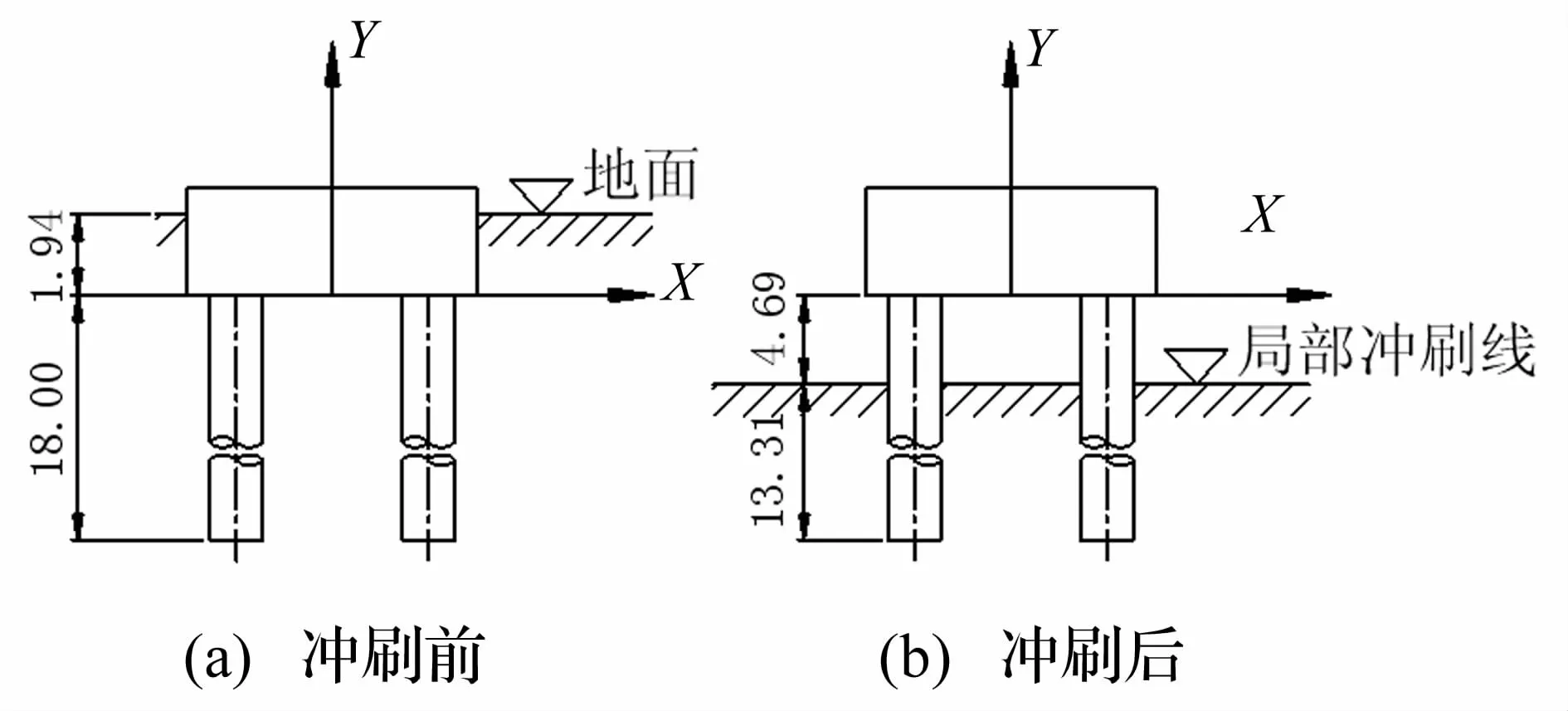
圖8 8＃墩沖刷前后的基礎(chǔ)埋深（單位：m）Fig．8 Variation of buried depth of 8＃pier（Unit：m）

圖9 群樁分布圖（單位：cm）Fig．9 Schematic diagram of pile-group（Unit：cm）

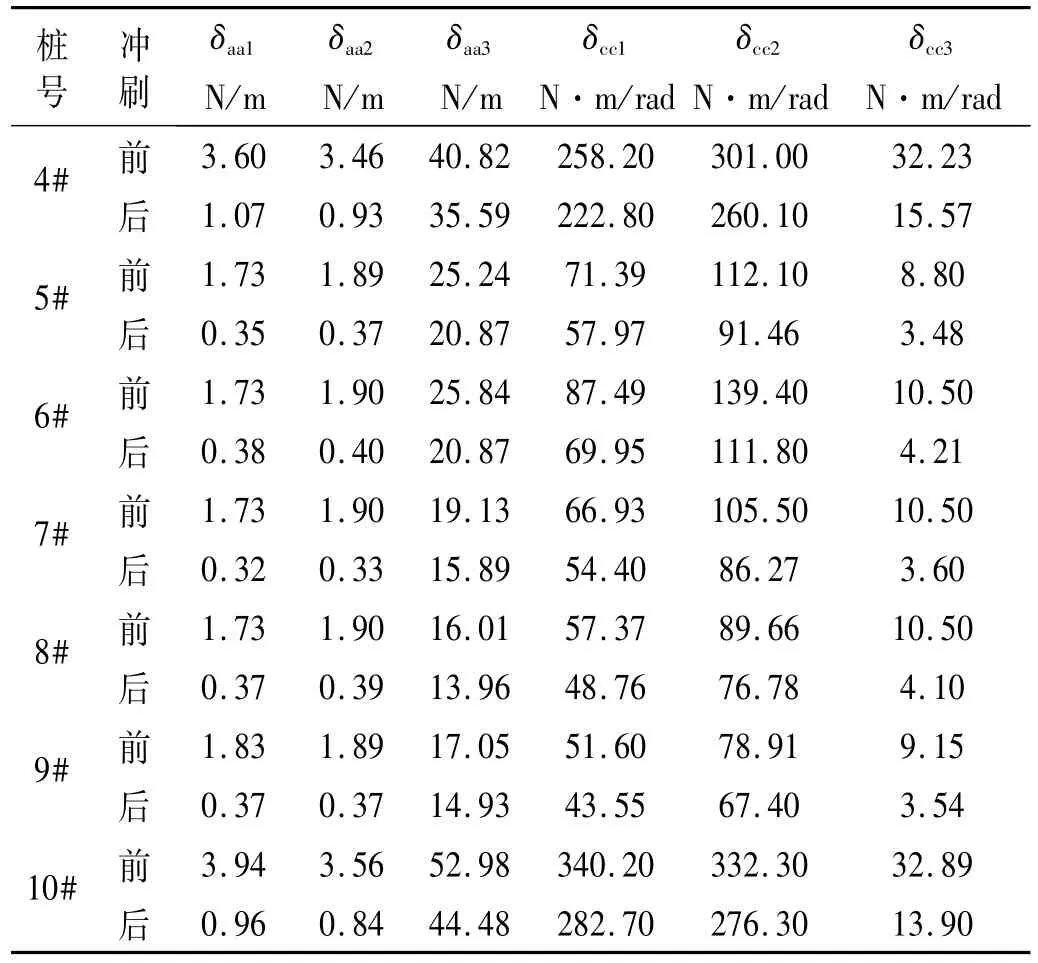
表4 沖刷前后各墩基礎(chǔ)等效剛度（×109）Tab．4 Equivalent stiffness of foundation before and after scouring

該橋樁基礎(chǔ)為鉆孔樁，樁端置于一定深度的弱風(fēng)化玄武巖中，各墩群樁分布如圖9所示。各墩基礎(chǔ)沖刷前后的等效剛度計(jì)算結(jié)果見(jiàn)表4。從表中結(jié)果可以看出，各墩基礎(chǔ)等效剛度在沖刷之后都減小，其中水平方向的平移剛度與豎向的抗扭剛度減小最顯著。沖刷之前，承臺(tái)側(cè)面受到土的抗力，沖刷之后，承臺(tái)全部暴露在水中，只有土中的樁基礎(chǔ)橫向受力，剛度必然顯著減小；該橋樁基礎(chǔ)為端承樁，豎向剛度主要受基底豎向承載力影響，沖刷僅減小了承臺(tái)底土的豎向抗力，對(duì)整體的豎向剛度的影響小于水平向剛度。

4．2 橋梁自振特性分析

通過(guò)有限元計(jì)算，得到該橋在沖刷前后的自振頻率及響應(yīng)振型，計(jì)算結(jié)果對(duì)比見(jiàn)表5。圖10～圖11所示為沖刷前后橋梁典型振型的振型圖。在兩聯(lián)連續(xù)梁和多孔簡(jiǎn)支梁中有部分梁的振型是獨(dú)立的。前10階振型大部分出現(xiàn)在兩端連續(xù)梁處，其中前3階振型都出現(xiàn)在邊跨（40＋64＋40）m連續(xù)梁處。沖刷之后，順橋向與橫橋向的一階模態(tài)頻率值均變小，一階縱漂頻率降低22．3%，一階橫彎頻率降低8．4%。河流沖刷使得基礎(chǔ)剛度減小，尤其是水平方向的剛度減小顯著，橋梁整體變得更柔，順橋向與橫橋向的自振頻率變低。

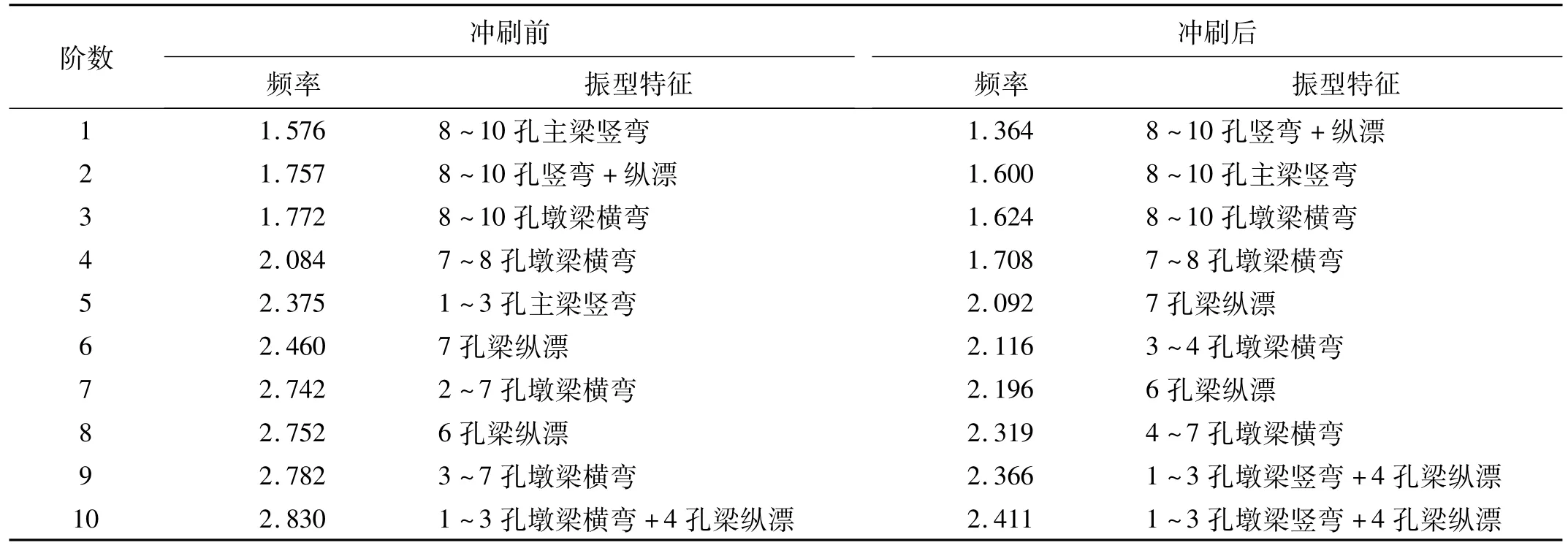
表5 自振頻率及振型Tab．5 Free vibration characteristic

圖10 沖刷前橋梁振型圖Fig．10 Mode shapes of bridge before scouring

圖11 沖刷后橋梁振型圖Fig．11 Mode shapes of bridge after scouring

4．3 車(chē)橋響應(yīng)分析

通過(guò)該橋的鐵道線路為客貨共線線路，由于貨車(chē)單位延長(zhǎng)重量遠(yuǎn)大于客車(chē)，其對(duì)橋梁基礎(chǔ)及周?chē)鷧^(qū)域產(chǎn)生的振動(dòng)亦大于客車(chē)，偏安全，計(jì)算中采用軸重較大的C70貨車(chē)，計(jì)算無(wú)機(jī)車(chē)50節(jié)編組以90 km／h過(guò)橋時(shí)引起的振動(dòng)狀態(tài)。采用德國(guó)低干擾譜轉(zhuǎn)換的時(shí)域不平順樣本作為軌道不平順激勵(lì)，截至波長(zhǎng)80m。

由于貨車(chē)車(chē)輛只有一系懸掛裝置，在建立車(chē)輛子系統(tǒng)模型時(shí)，將公式（10）各矩陣中有關(guān)轉(zhuǎn)向架自由度的行與列去掉即可。

計(jì)算中各工況時(shí)程積分的時(shí)間步長(zhǎng)均為0．02 s。橋梁系統(tǒng)的阻尼按Rayleigh阻尼考慮，計(jì)入橋梁的一階橫向頻率和一階豎向頻率。偏安全起見(jiàn)，各階頻率的阻尼比均取0．02。

如表6所示為沖刷前后車(chē)輛的最大振動(dòng)響應(yīng)結(jié)果，可以看出，沖刷前后列車(chē)行車(chē)時(shí)脫軌系數(shù)、輪軸橫向力與車(chē)體加速度都小于容許值，橫向與豎向平穩(wěn)性達(dá)到優(yōu)良的等級(jí)；橋墩基礎(chǔ)受到?jīng)_刷之后，車(chē)輛的動(dòng)力響應(yīng)普遍增大，其中車(chē)體橫向加速度變化最顯著，最大值增大64%。輪重減載率在沖刷之間已經(jīng)接近容許值，在沖刷之后值為0．64，超過(guò)了容許限值，影響行車(chē)安全。河流沖刷引起樁基礎(chǔ)的剛度變化導(dǎo)致整個(gè)橋梁的振動(dòng)模態(tài)發(fā)生變化，從而對(duì)車(chē)體的響應(yīng)也造成影響，基礎(chǔ)水平剛度的減小使得車(chē)體的橫向響應(yīng)變化顯著。

表6 沖刷前后車(chē)輛動(dòng)力響應(yīng)Tab．6 Dynamic responses of vehicle

表7給出了沖刷前后各梁的橋梁動(dòng)力響應(yīng)最大值。圖12～圖14給出了第2孔梁、第7孔梁與第9孔梁跨中的動(dòng)力響應(yīng)時(shí)程。

橋墩基礎(chǔ)在受到?jīng)_刷之后橋梁各跨跨中豎向位移變化不大，豎向加速度略有減小，由于河流沖刷對(duì)于群樁基礎(chǔ)豎向剛度影響較小，從而對(duì)橋梁豎向動(dòng)力響應(yīng)的影響不顯著。

橫向位移與橫向加速度時(shí)程曲線呈現(xiàn)啞鈴狀，連續(xù)梁比簡(jiǎn)支梁更為明顯。分析認(rèn)為這是列車(chē)荷載突加突減引起的，列車(chē)長(zhǎng)度大于橋梁長(zhǎng)度，列車(chē)第一節(jié)車(chē)上橋與最后一節(jié)車(chē)出橋，使橋梁受到突加荷載與突減荷載，在跨中處沖擊效應(yīng)最大。沖刷之后，結(jié)構(gòu)剛度變小，沖擊效應(yīng)減弱。連續(xù)梁跨度大于簡(jiǎn)支梁使得效應(yīng)突增段比簡(jiǎn)支梁明顯。

沖刷前后，橫向位移與橫向加速度有顯著變化。中部第4孔～第7孔簡(jiǎn)支梁橋墩基礎(chǔ)受到?jīng)_刷之后橫向位移與橫向加速度都明顯增大，其中第7孔梁橫向動(dòng)力響應(yīng)增加最為顯著，橫向位移增大1．44倍，橫向加速度增加84%。河流沖刷使得橋梁水平方向剛度減小，橫向車(chē)致振動(dòng)響應(yīng)增大。

兩聯(lián)連續(xù)梁橋的橫向響應(yīng)時(shí)程曲線形狀差異較大。第1、第2、第9、第10孔梁在橋墩基礎(chǔ)沖刷之后橫向位移與橫向加速度都減小，其中第2孔梁橫向位移幅值減小54%，橫向加速度幅值減小67%。橋梁橫向響應(yīng)振型在沖刷之前基本是獨(dú)立的，而沖刷之后與簡(jiǎn)支梁耦合在一起。在1～3孔連續(xù)梁體系中，沖刷后第3孔梁與簡(jiǎn)支梁剛度減小，而第1、2孔梁剛度下降不顯著，故此連續(xù)梁振型形狀有較大改變。沖刷前后橋梁橫向振動(dòng)能量基本保持不變，由于第3孔梁振動(dòng)加劇，因而第1、2孔梁振幅反而有所下降。8～10孔梁在沖刷之后橫向自振頻率降低，橫向響應(yīng)的變化除與1～3孔梁相同的原因外，還有車(chē)橋體系共振的因素。車(chē)體橫向一階自振頻率為1．809Hz。沖刷之前，橋梁第3階頻率為1．772Hz，與車(chē)體的橫向自振頻率接近，當(dāng)列車(chē)經(jīng)過(guò)橋梁時(shí)發(fā)生橫向共振作用。梁的第3階頻率振型獨(dú)立，為8～10孔梁橫彎振型，對(duì)中間簡(jiǎn)支梁影響不大。而在沖刷之后，梁的各階橫向頻率及其諧波頻率均遠(yuǎn)離車(chē)體橫向自振頻率，未發(fā)生共振。第9、第10孔梁橋墩未直接受到河流沖刷，河流沖刷作用的影響較小，受共振作用影響大。故沖刷之后，第9、10孔梁的橫向響應(yīng)減小。

表7 橋梁動(dòng)力響應(yīng)最大值Tab．7 Maximum dynamic responses of bridge

圖12 2號(hào)梁跨中動(dòng)力響應(yīng)時(shí)程Fig．12 Dynamic responses of 2＃span

圖13 7號(hào)梁跨中動(dòng)力響應(yīng)時(shí)程Fig．13 Dynamic responses of 7＃span

圖14 9號(hào)梁跨中動(dòng)力響應(yīng)時(shí)程Fig．14 Dynamic responses of 9＃span

5 結(jié) 論

本文計(jì)算了群樁基礎(chǔ)的沖刷深度，采用地基系數(shù)法計(jì)算群樁承臺(tái)基礎(chǔ)的等效剛度。在橋墩墩底以多自由度彈簧約束模擬基礎(chǔ)等效剛度，建立了考慮河流沖刷作用的車(chē)橋耦合動(dòng)力分析模型，采用全過(guò)程迭代方法求解系統(tǒng)方程。得出以下結(jié)論：

（1）在沖刷之后，全部橋墩承臺(tái)底面均高于沖刷線，橋墩基礎(chǔ)由低承臺(tái)基礎(chǔ)變成高承臺(tái)基礎(chǔ)，各墩基礎(chǔ)等效剛度在沖刷之后都減小，其中水平方向的平移剛度與豎向的抗扭剛度減小最顯著。

（2）橋墩基礎(chǔ)受到?jīng)_刷之后，車(chē)輛動(dòng)力響應(yīng)普遍增大，其中車(chē)體橫向加速度變化最顯著，最大值增大62%。

（3）邊跨連續(xù)梁未受沖刷梁跨，在整個(gè)橋梁受到河流沖刷之后橫向響應(yīng)減小，其中第2孔梁橫向位移減小54%，橫向加速度減小67%；簡(jiǎn)支梁受沖刷之后跨中橫向位移與橫向加速度明顯增大，其中7＃梁橫向動(dòng)力響應(yīng)增加最為顯著，橫向位移增大1．44倍，橫向加速度增加84%。

（4）鐵路橋梁跨越江海時(shí)廣泛采用群樁承臺(tái)基礎(chǔ)，易受到水流沖刷的影響，應(yīng)對(duì)橋梁結(jié)構(gòu)的樁基、承臺(tái)進(jìn)行合理設(shè)計(jì)，并使用考慮水流沖刷作用的模型進(jìn)行動(dòng)力仿真以保證行車(chē)的平穩(wěn)性和安全性。

［1］李夢(mèng)龍．潮流作用下橋墩局部沖刷研究［D］．天津：天津大學(xué)，2012．

［2］沈周．鐵路橋梁擴(kuò)展基礎(chǔ)沖刷探測(cè)與穩(wěn)定性分析［D］．長(zhǎng)沙：中南大學(xué)，2006．

［3］吳定俊，周建民，余華．高速鐵路橋梁梁墩基礎(chǔ)體系列車(chē)過(guò)橋動(dòng)力分析［J］．上海鐵道大學(xué)學(xué)報(bào)，2000，21（10）：44－49．WU Ding-jun，ZHOU Jian-min，YU Hua．Dynamic analysis of vehicle-bridge system including pier and foundation［J］．Journal of Shanghai Tiedao University，2000，21（10）：44－49．

［4］蔣通，馬超勇，張昕．彈性支撐條件下車(chē)－橋體系的振動(dòng)分析［J］．力學(xué)季刊，2004，25（2）：256－263．JIANG Tong， MA Chao-yong， ZHANG Xin． Dynamic analysis of train-bridge system with elastic supports［J］．Chinese Quarterly of Mechanics，2004，25（2）：256－263．

［5］單德山，李喬．考慮樁土作用的鐵路曲線梁橋車(chē)橋耦合振動(dòng)分析［J］．重慶交通學(xué)院學(xué)報(bào)，2004，23（6）：10－14．SHAN De-shan，LI Qiao．Coupled vibration analysis of railway simple-supported curved-girder bridges and vehicles with soil-structure interaction［J］．Journal of Chongqing Jiaotong University，2004，23（6）：10－14．

［6］李小珍，劉德軍，晉智斌．大跨度鐵路懸索橋車(chē)－線－橋耦合振動(dòng)分析［J］．鋼結(jié)構(gòu)，2010，25（140）：6－12．LI Xiao-zhen，LIU De-jun，JIN Zhi-bin．Analysis of traintrack-bridge coupled vibration of a railway long-span suspension bridge［J］．Steel Construction，2010，25（140）：6－12．

［7］周泳濤，高正榮，鮑衛(wèi)剛．復(fù)雜群樁基礎(chǔ)沖刷計(jì)算方法研究［J］．公路，2012，（4）：26－29．ZHOU Yong-tao，GAO Zheng-rong，BAO Wei-gang．A study on erosion calculation method of complex pile group foundation［J］．Highway，2012，（4）：26－29．

［8］中華人民共和國(guó)鐵道部．TB 10017－99鐵路工程水文勘測(cè)設(shè)計(jì)規(guī)范［S］．北京：中國(guó)鐵道出版社，1999．

［9］中華人民共和國(guó)鐵道部．TB 10002．5－2005鐵路橋涵地基和基礎(chǔ)設(shè)計(jì)規(guī)范［S］．北京：中國(guó)鐵道出版社，2005．

［10］張楠，夏禾，程潛，等．制動(dòng)力作用下車(chē)輛－車(chē)站結(jié)構(gòu)耦合動(dòng)力分析［J］．振動(dòng)與沖擊，2011，30（2）：138－143．ZHANG Nan，XIA He，CHENG Qian， et al． Analysis method for a vehicle coupled system under braking force［J］．Journal of Vibration and Shock，2011，30（2）：138－143．

［11］ Zhang N．Xia H．et al．A vehicle-bridge linear interacted model and its validation ［J］． International Journal of Structural Stability and Dynamics，2010，10（2）：335－361．

［12］夏禾，張楠．車(chē)輛與結(jié)構(gòu)動(dòng)力相互作用［M］．2版．北京：科學(xué)出版社，2005．

［13］ Xia H，Zhang N，Guo W．W．Application of train-bridge interaction analysis to bridge design of high-speed railways in China［C］．Proceedings of ISEV2009．Beijing：Science Press，2009：965－975．

［14］Zhai W M，Xia H，Cai C B．High-speed train-track-bridge dynamic interactions-Part I：theoretical model and numerical simulation［J］．International Journal of Rail Transportation，2013，1（2）：3－24．

［15］ Zhai W M，Wang S L，Zhang N．High-speed train-trackbridge dynamic interactions-Part II：experimental validation and engineering application［J］．International Journal of Rail Transportation，2013，1（2）：25－41．

［16］翟婉明．車(chē)輛－軌道耦合動(dòng)力學(xué)［M］．3版．北京：科學(xué)出版社，2007．

［17］張楠，夏禾．基于全過(guò)程迭代的車(chē)橋耦合動(dòng)力系統(tǒng)分析方法［J］．中國(guó)鐵道科學(xué)，2013，34（5）：32－38．ZHANG Nan，XIA He．A vehicle-bridge interaction dynamic system analysis method based on inter-system iteration［J］．China Railway Science，2013，34（5）：32－38．