全息數據外推與插值技術的極限學習機方法

孫超, 何元安, 商德江, 劉月嬋

(1.哈爾濱工程大學 動力與能源工程學院，黑龍江 哈爾濱 150001；2.哈爾濱工程大學 水聲工程學院，黑龍江 哈爾濱 150001；3.船舶系統工程研究院，北京 100036)

近場聲全息技術[1-4](near-field acoustic holography ，NAH)是一種研究噪聲源識別和聲場輻射問題的重要技術。通過測量聲源表面附近的聲場信息，逆向重建聲源表面的各種聲學量，進而重建聲源外部三維聲場。該技術用于水下結構振動的非接觸探測和輻射噪聲測量，聲像清晰，噪聲特性分析詳盡，能夠識別主要激勵源，從而有效指導噪聲控制方案。因此，該技術發展很快，并被應用于實際工程中。由于算法自身限制，通常要求全息測量孔徑至少為聲源尺寸2倍以上，以保證孔徑邊緣的聲壓得到足夠的衰減，從而減小孔徑有限性導致的誤差。另外，對于大尺寸或結構復雜聲源所產生的聲場，測量時通常要布置較多測點，但需要大量的傳感器和采集設備，使測量工作量大大增加，在一定程度上也限制了NAH技術的應用。近年來，局部近場聲全息技術(patch NAH)的興起在一定程度上突破了測量孔徑的限制，可以在小孔徑條件下實施NAH技術，從而為大尺寸聲源重建提供了可能。全息數據外推就是一種典型的局部近場聲全息技術，通過對較小測量孔徑內的聲壓數據進行外推，獲得了較大孔徑內的聲壓數據近似值，間接地增大了測量孔徑，從而減小了有限孔徑效應對全息重建精度的影響。國內外都有相關學者對此問題已進行了較深入地研究，取得了較多成果[5-12]。

針對神經網絡極限學習機算法(extreme learning machine，ELM)具有逼近非線性函數的能力，使其適用于解決信號處理過程中的分類辨識和回歸擬合問題。本文將其與NAH技術相結合，提出了一種基于極限學習機的全息數據外推與插值技術。

1 極限學習機(ELM)理論

常規的神經網絡主要有前饋、反饋和局部逼近神經網絡。其中，單隱層前饋神經網絡以其良好的學習性能在許多領域中得到了廣泛應用。極限學習機ELM算法[13-15]是單隱層前饋神經網絡的新算法，該算法隨機產生輸入層與隱含層之間的連接權值和隱含層神經元的閾值。在訓練過程中，只需要設定隱含層神經元個數，便可獲得唯一最優解。該方法與傳統訓練方法相比具有學習速度快、泛化性能好等優點。典型的單隱層前饋神經網絡結構如圖1所示。

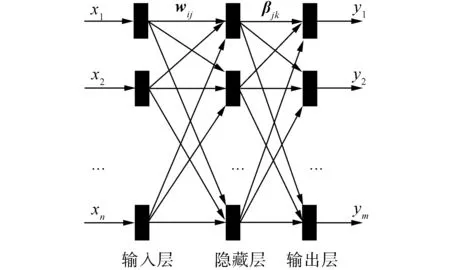
圖1 單隱層前饋神經網絡結構

網絡由輸入層、隱含層和輸出層組成，輸入層與隱含層及隱含層與輸出層間由神經元連接。設輸入層有n個神經元，對應n個輸入變量；隱含層有L個神經元；輸出層有m個神經元，對應m個輸出變量，設輸入層與隱含層間的連接權值為w，隱含層與輸出層間的連接權值為β,隱含層神經元閾值為b,則w、β、b可表示為

其中，wji為輸入層第i個神經元與隱含層第j個神經元間的連接權值,βjk為隱含層第j個神經元與輸出層第k個神經元間的連接權值。設隱含層神經元的激活函數為g(x)，則網絡輸出為

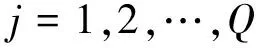
(1)

式中：Q為訓練集的樣本數，wi=[wi1wi2…win]，xj=[x1jx2j…xnj]T為訓練樣本，上式可表示為

(2)

H稱為神經網絡的隱含層輸出矩陣，表達式為

(3)

在此基礎上，由Huang等[20]提出的定理可知當激活函數g(x)無限可微時，單隱含層前饋神經網絡的參數w和b在訓練前可以隨機選擇，且在訓練過程中保持不變。隱含層與輸出層之間的連接權值β可以通過求解下面方程組獲得

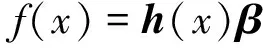
(4)

式中：h(x)為測試集的隱含層輸出矩陣。Huang等給出當訓練樣本數遠大于隱含層節點數時有：

(5)

否則

(6)

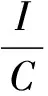
(7)

式中:K(u,v)為核函數，通常采用徑向基核函數

(8)

對于參數C和γ，采用交叉驗證方法尋找其最佳值，然后利用最佳參數訓練模型。通過引入核函數，避免了選擇隱含層神經元個數和定義隱含層的輸出矩陣，進一步提高了ELM的學習速度和泛化能力。本文即采用這種基于核函數的ELM對全息數據外推和插值問題進行研究。

2 基于ELM的全息數據外推與插值

如圖2所示，由測量區域S1中的測點聲壓外推區域S2-S1中的未測點聲壓，并保證預測值和盡可能接近真實值。將外推值與測量值組合獲得更大全息孔徑內的聲場信息，相當于間接增大了全息測量面。這樣，有效地減小了測量孔徑，降低工作量，并提高了重建精度。

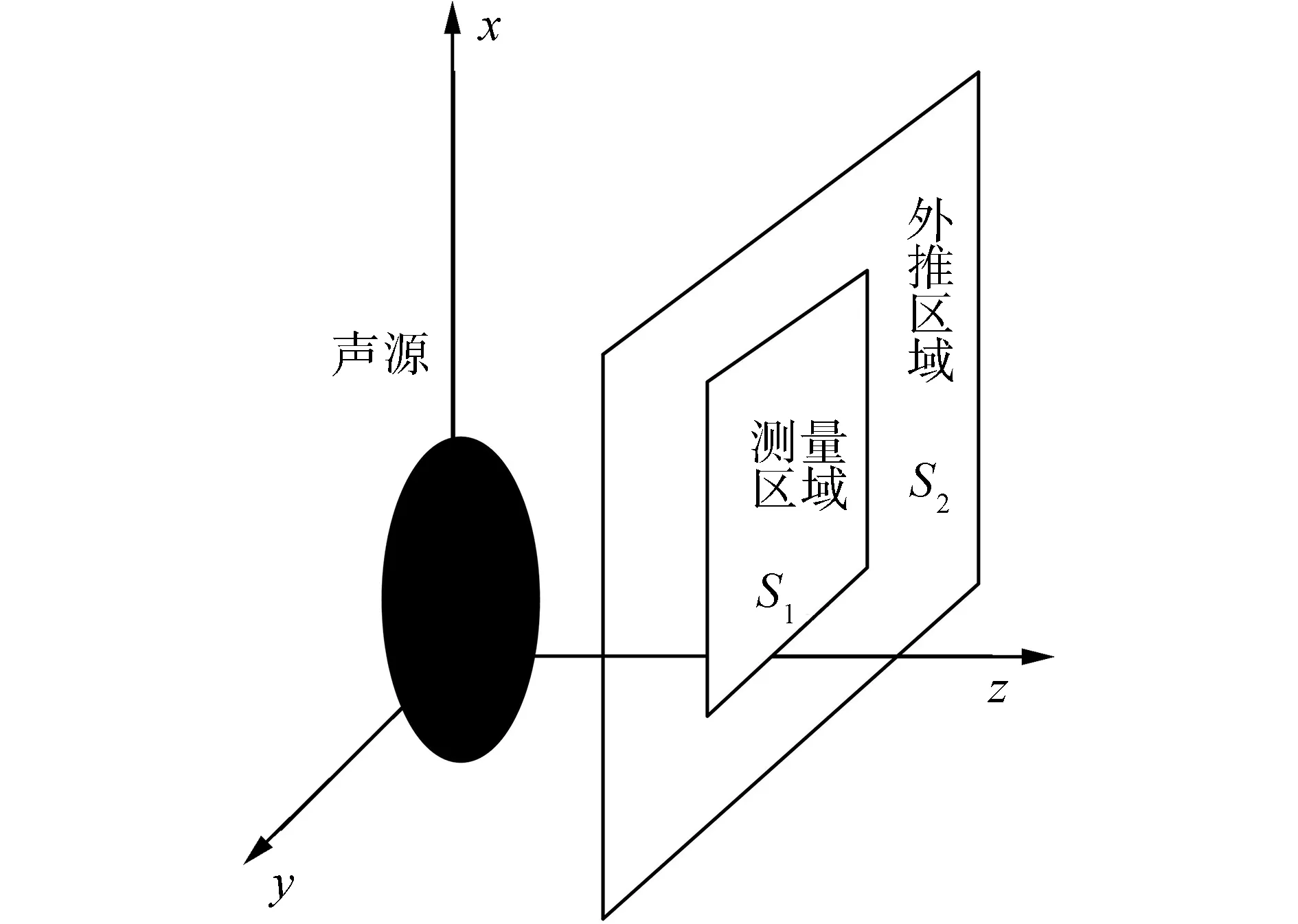
圖2 全息數據外推示意圖

概括起來，基于ELM的數據外推主要為以下步驟:1)選取測量區域S1中的坐標Xs、Ys和復聲壓作為訓練樣本集，其中坐標值為網絡的輸入值，而復聲壓的實部或虛部分別作為網絡輸出值，這樣就構造出兩類不同的網絡并進行訓練；2)根據需要外推的區域S2-S1確定位置坐標(Xpn,Ypn)，n為預測的點數，同訓練樣本集中的坐標組成預測樣本集中的輸入值，輸入至前面訓練好的網絡。網絡的輸出值為要預測的目標值，即擴展后的全息面S2上的聲壓實部和虛部，并保持初始全息面S1上的數據不變；3)根據外推后全息數據進行NAH計算，插值步驟與外推相似，插值區域為全息測量面S1測點間的插入點。

3 數值仿真

3.1 全息數據外推

首先驗證該方法在解決全息數據外推問題的有效性。設平面內有2點聲源，坐標分別為(0.2,0.2,0)和(-0.2,-0.2,0)，兩聲源強度比為2∶1。測量面位于z=0.1 m，尺寸0.3 m×0.3 m(-0.15 m≤x≤0.15 m,-0.15 m≤y≤0.15 m), 測點間隔0.025 m,包含13×13個測點。外推面0.5 m×0.5 m(-0.25 m≤x≤0.25 m,-0.25 m≤y≤0.25 m)包含21×21個測點。分析頻率為500、1 800、3 000 Hz。為了比較外推數據的準確性，定義外推誤差公式：

(9)

式中：pt為各點理論復聲壓，Pa;pe為外推得到的全息面復聲壓,Pa。結果見圖3。圖中白色方框為初始全息測量孔徑，由于全息面較小，測量孔徑并未能完全覆蓋聲壓峰值位置。通過外推方法，聲場的輻射區域都被較好地恢復，外推結果與理論值基本一致。測量未得到的峰值區域得到了準確恢復，并且峰值和位置和理論值很相似。外推誤差分別為7.91%、7.54%和12.43%。測量面的全息數據經外推后共441個測點，與實測點數相比增加1.6倍，說明本方法能夠有效增大測量孔徑的聲場外推方法。

(a) 500 Hz理論聲壓

(b) 500 Hz外推聲壓

(c)1 800 Hz理論聲壓

(d) 1 800 Hz外推聲壓

(e) 3 000 Hz理論聲壓

(f) 3 000 Hz外推聲壓

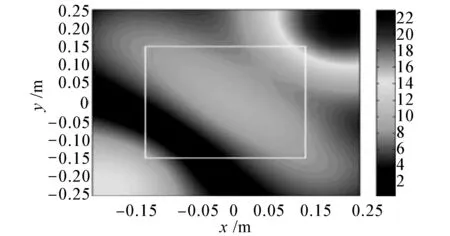
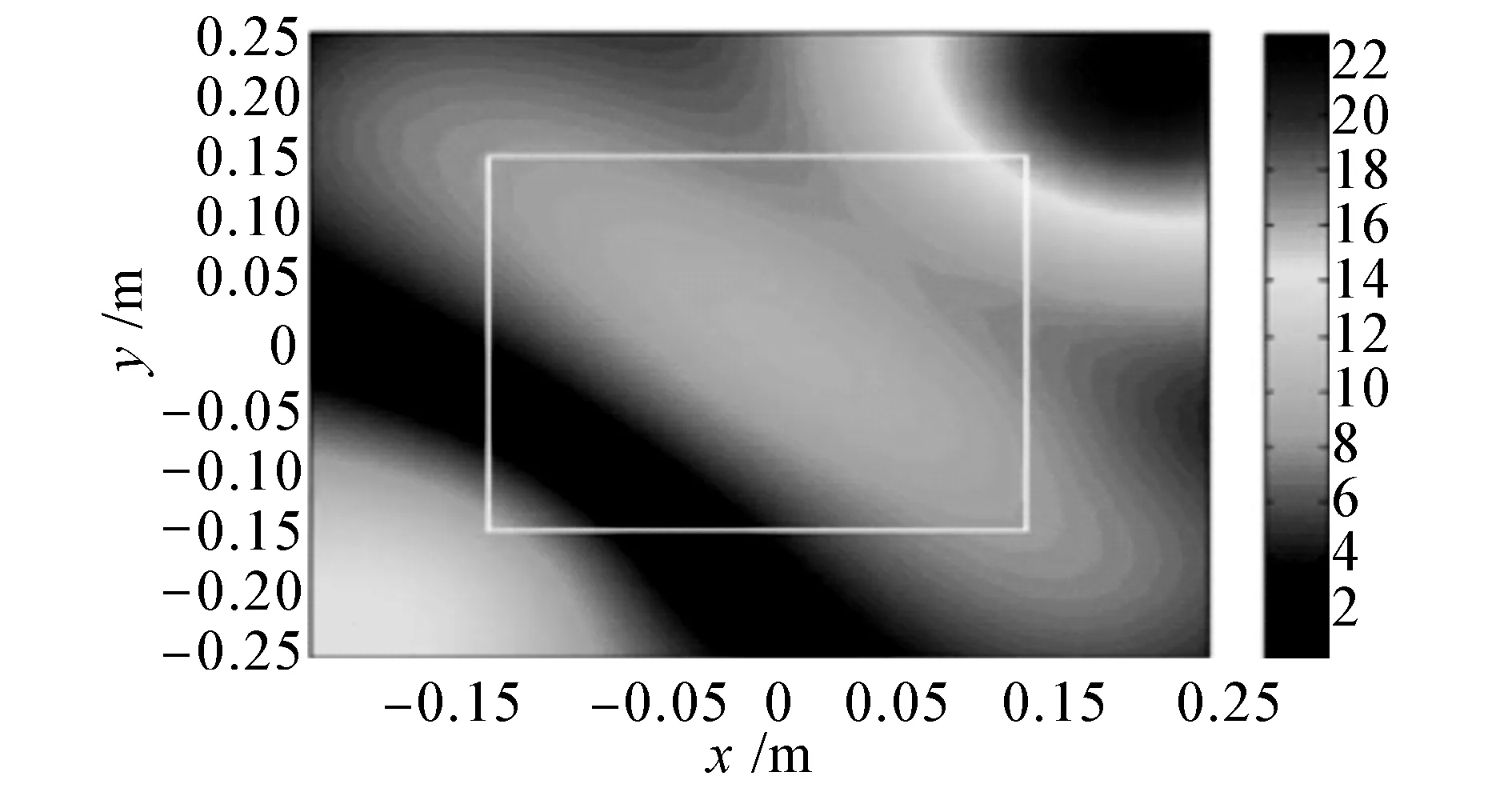
接下來采用四周為無限大障板上的簡支平板作為研究對象，平板在空氣中受簡諧力激勵。選取參數如下：鋼板長寬均為0.6 m，厚度為0.006 m，密度為7.8×103kg/m3，楊氏模量E=2.1×1011N/m2。選取板所在平面為z=0 m,全息面位置為z=0.06 m的平面。中心為坐標原點，激勵點位置在(-0.05 m,-0.04 m)，激勵力幅值為5 N，頻率分別為200、500、600、1 000 Hz。長寬方向的測量間隔均為0.025 m。全息面上S1的尺寸為-0.2 m≤x≤0.2 m,-0.2 m≤y≤0.2 m;擴展后的區域-0.3 m≤x≤0.3 m,-0.3 m≤y≤0.3 m。測量面S1共包含17×17個測點，擴展面S2共包含25×25個測點。計算過程中信噪比為30 dB，其中白色矩形框為S1中的仿真聲壓測量數據，采用ELM方法外推S2中的聲壓數據。測量面上復聲壓采用瑞利第一積分計算得出。另外，為分析本方法在較小測量孔徑下聲場外推精度，將全息測量孔徑減少為0.3 m×0.3 m (-0.15 m≤x≤0.15 m,-0.15 m≤y≤0.15 m)，測點間隔仍為0.025 m，擴展后的區域為0.6 m×0.6 m (-0.3 m≤x≤0.3 m,-0.3 m≤y≤0.3 m)，即由13×13個測點外推25×25個測點。這里只給出600 Hz和1 kHz的仿真結果，見圖4和圖5，外推誤差詳見表1。

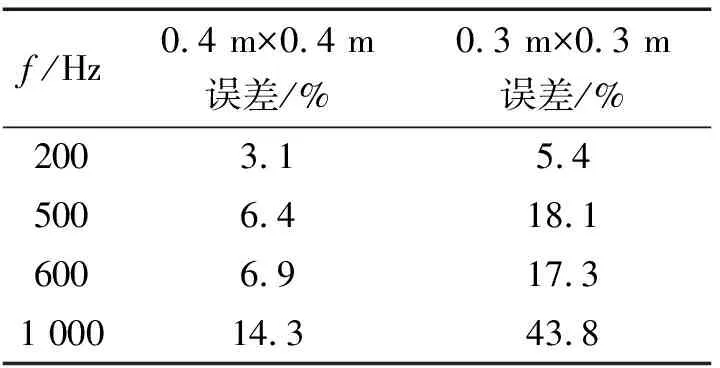
表1 不同全息孔徑數據外推誤差

能夠看到，通過聲場外推得到的聲壓分布峰值與理論值相比精度依然較高。不同頻率全息面的聲場外推結果與理論值吻合得較好。在較低頻率時，外推精度較高；當頻率變大時，聲場分布變得復雜，精度有所下降。當輸入的全息數據變少時，該方法的外推效果依然較好,全息數據經外推后與實際測點相比增加了456個測點。但高頻時由于聲場信息獲取較少，外推精度有所下降。

(a) 600 Hz理論聲壓

(b) 600 Hz外推聲壓

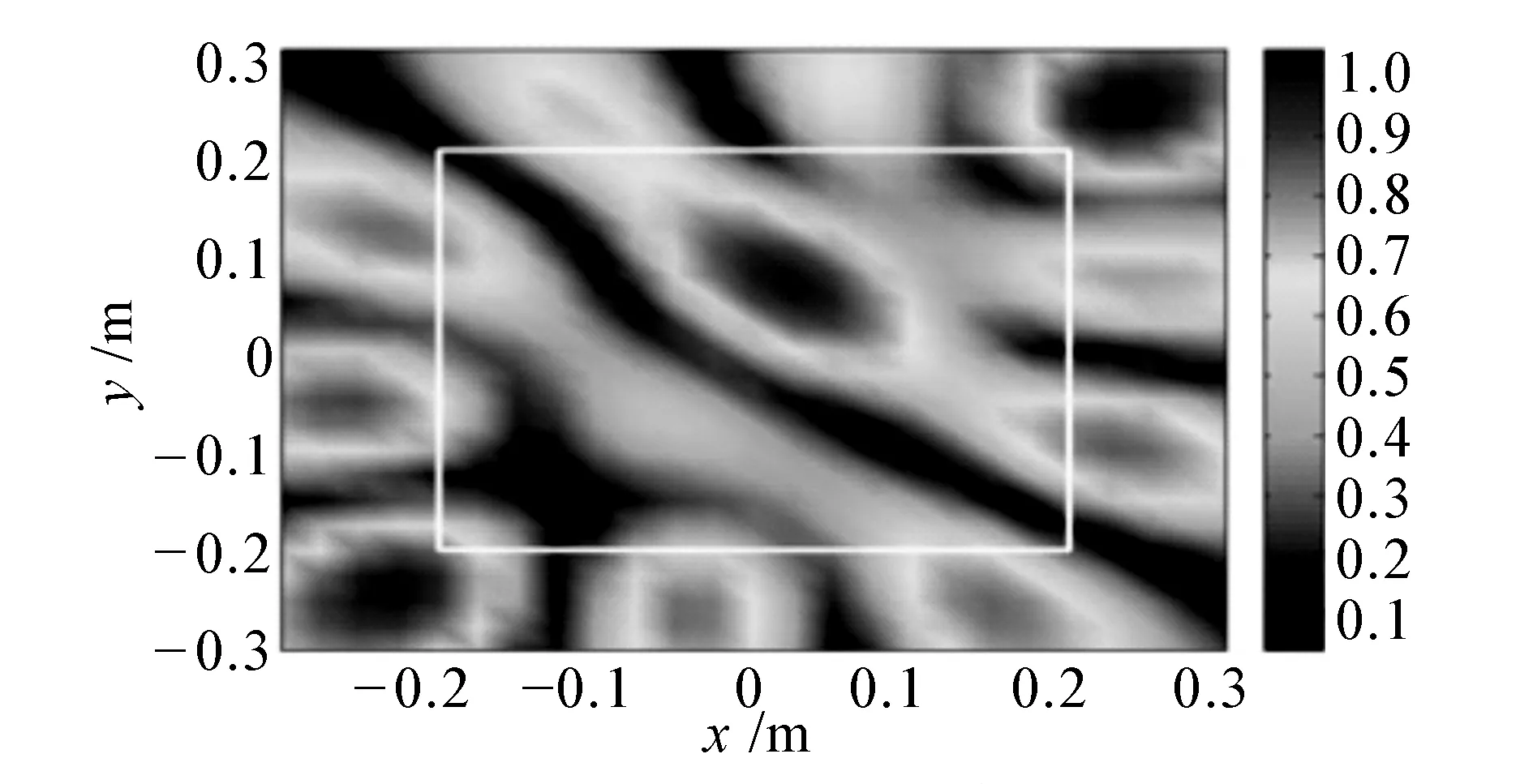
(c)1 000 Hz理論聲壓

(d) 1 000 Hz外推聲壓

(a) 1 000 Hz測量聲壓幅值

3.2 采用外推數據重建聲場

在前面平板輻射聲場外推的基礎上，基于外推數據采用統計最優近場聲全息(SONAH)進行重建，并與基于初始測量值的重建效果和重建面的理論值相比較。全息面尺寸0.3 m×0.3 m，重建面位于z=0.02 m，大小0.6 m×0.6 m，其他參數不變。不同頻率得到的重建誤差見表2。

可以看到在不同頻率時，采用基于初始測量值的重建聲場和理論值相比誤差較大，而采用基于ELM數據外推得到的全息面數據進行聲場重建效果較好，重建精度提高很多。隨著頻率升高，誤差逐漸變大，這是由于聲場外推的精度隨著頻率的升高而下降造成的，但仍比外推前的效果要好，表明該方法是一種有效的Patch NAH技術。

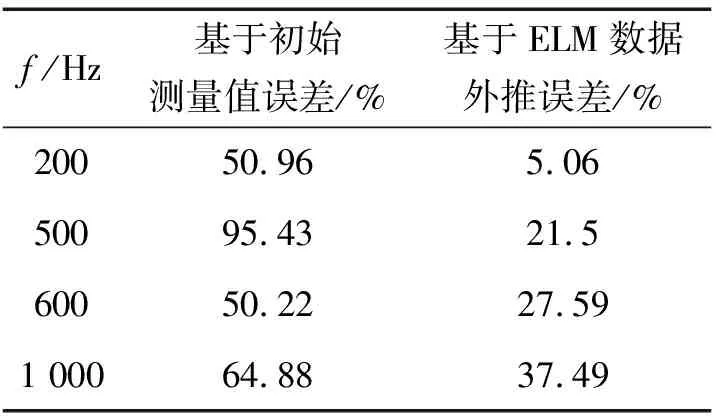
表2 不同全息孔徑數據外推誤差

3.3 全息數據插值

仍采用單點激勵無限大障板上的簡支平板作為研究對象，測量參數和平板參數與上節相同。文中給出1 kHz時插值前后的聲壓幅值，見圖5所示,表3給出不同頻率時插值聲壓與理論聲壓的誤差。為了比較方法的有效性及插值點個數對插值精度的影響，將全息面測點間隔設為0.05、0.1、0.15 m，插值后間隔0.025 m，即分別由13×13個、7×7個和5×5個的測點網格插值為25×25個虛擬網格。

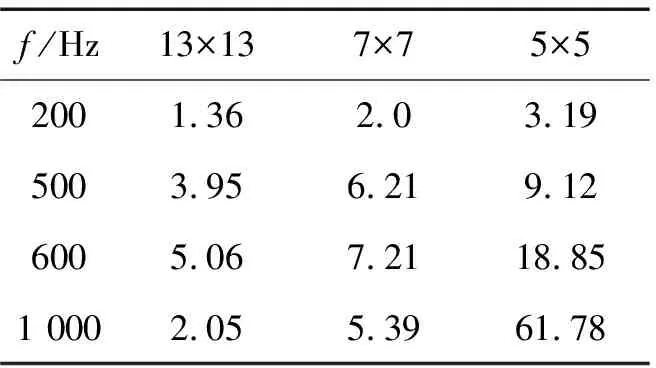
表3 不同全息數據的插值精度

通過比較可知，基于ELM的插值方法在低頻時精度較高，與理論聲壓相比誤差很小；隨著頻率的升高，5×5個全息數據輸入時將導致方法失效，這是由于頻率升高，波長變小，單位波長內采集到的聲場信息較少，而高頻時聲場更為復雜，需要更多的聲場數據。當輸入數據量增大時，插值精度顯著提高，誤差基本在10%以內，達到了預期效果。通過數值計算可知，該方法對于提高NAH采集效率進而提高NAH的重建精度是很有效的。

3.4 采用插值數據重建聲場

采用上節7×7個測點，結合SONAH算法進行全息重建，并與采用插值后25×25個虛擬測點重建的結果進行對比。重建面位于z=0.02 m，其他參數不變。圖6給出f=500 Hz情況下重建聲壓幅值對比。可以看出，插值后的全息面精度和重建圖像的空間分辨率均明顯提高，4個不同頻率插值后的重建誤差分別為4.05%、17.64%、23.9%和31.54%。

(a) 插值前重建面聲壓幅值

(b) 插值后重建面聲壓幅值

(c)重建面理論聲壓幅值

3.5 基于ELM的有限空間聲場插值

基于ELM的聲場插值技術除了可以將自由聲場插值外，也可用于非自由聲場插值。應用聲學有限元軟件ACTRAN對有限空間內聲場進行仿真，有限元模型為邊長1 m的立方體網格,如圖7所示。

圖7 非自由聲場仿真

仿真過程中將其中一平面(圖7中上表面)始終設置為水-空氣界面，另外5個表面通過設置不同導納使其滿足阻抗邊界、絕對軟邊界和絕對硬邊界(反射系數分別為0.5、-1、1)。在立方體水域中聲場由3個同相相干點源產生，點源位置分別為(0.1,0,0)、(-0.1,0,0)和(0.4,0,0)，源強之比為1∶2∶1。全息面為半徑為0.25 m的柱面測量面，長0.8 m，分析頻率100～3 000 Hz。按照下面4種不同測點情況對不同邊界條件聲場進行插值：1)軸向間隔0.1 m，周向間隔18°；2)軸向間隔0.1 m，周向間隔36°；3)軸向間隔0.2 m，周向間隔18°；4)軸向間隔0.2 m，周向間隔36°。將每種測點均插值成為軸向間隔0.05 m，周向間隔18°的測量面，因此插值后每測量面有340個測點，將插值后的結果與理論值進行對比得到插值誤差見圖8所示。

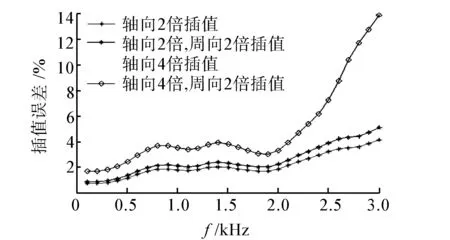
(a) 阻抗邊界

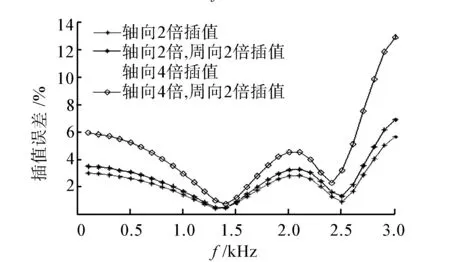
(b) 絕對軟邊界

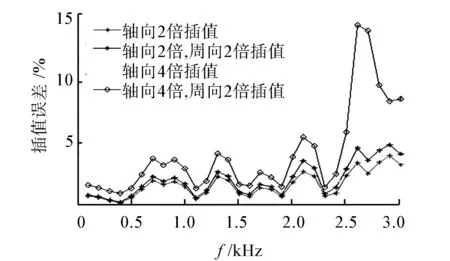
(c)絕對硬邊界

可以看到，在2 500 Hz以下不同邊界的聲場插值誤差均小于6%，精度較高；隨著頻率的升高，誤差逐漸變大，這是由于隨著頻率的升高，聲波波長逐漸變小，在單位波長內的測點個數也逐漸變少，由于測點信息的不足導致了插值的精度有所下降。另外，從圖中也能發現軸向插值倍數對插值精度的影響較大，誤差隨著軸向插值倍數的增加而變大，而周向插值倍數則影響較弱。當測量點個數為2)情況時，此時只有90個測點，通過插值得到了340個測點，且不同頻率的誤差都在5%以下。可見，通過聲場插值可以大大節省工作量，提高了工作效率。

(a) 阻抗邊界插值前聲壓幅值

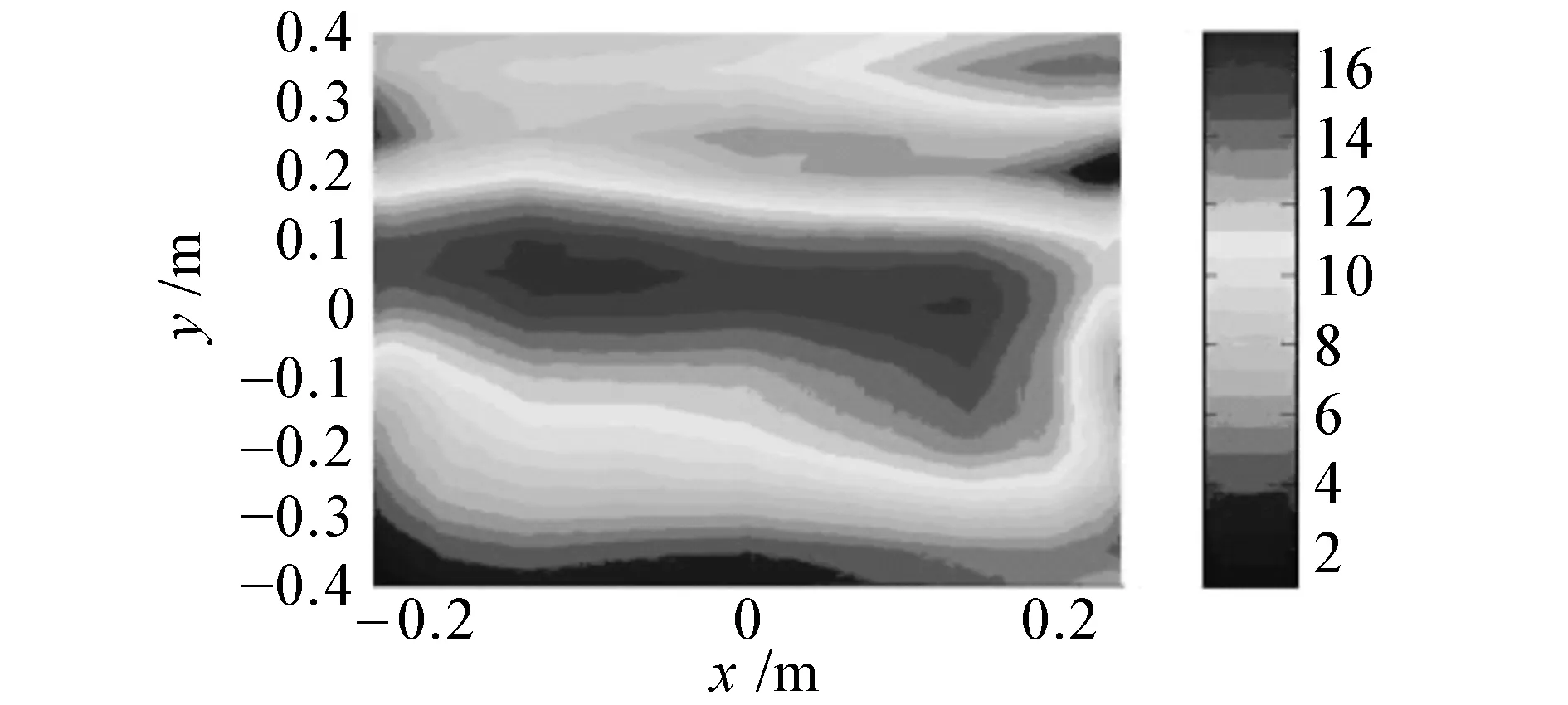
(b) 阻抗邊界理論聲壓幅值

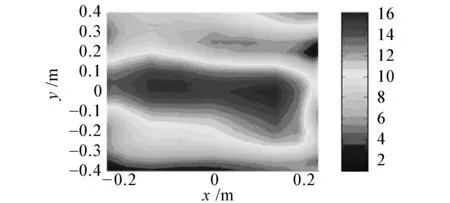
(c)阻抗邊界插值后聲壓幅值

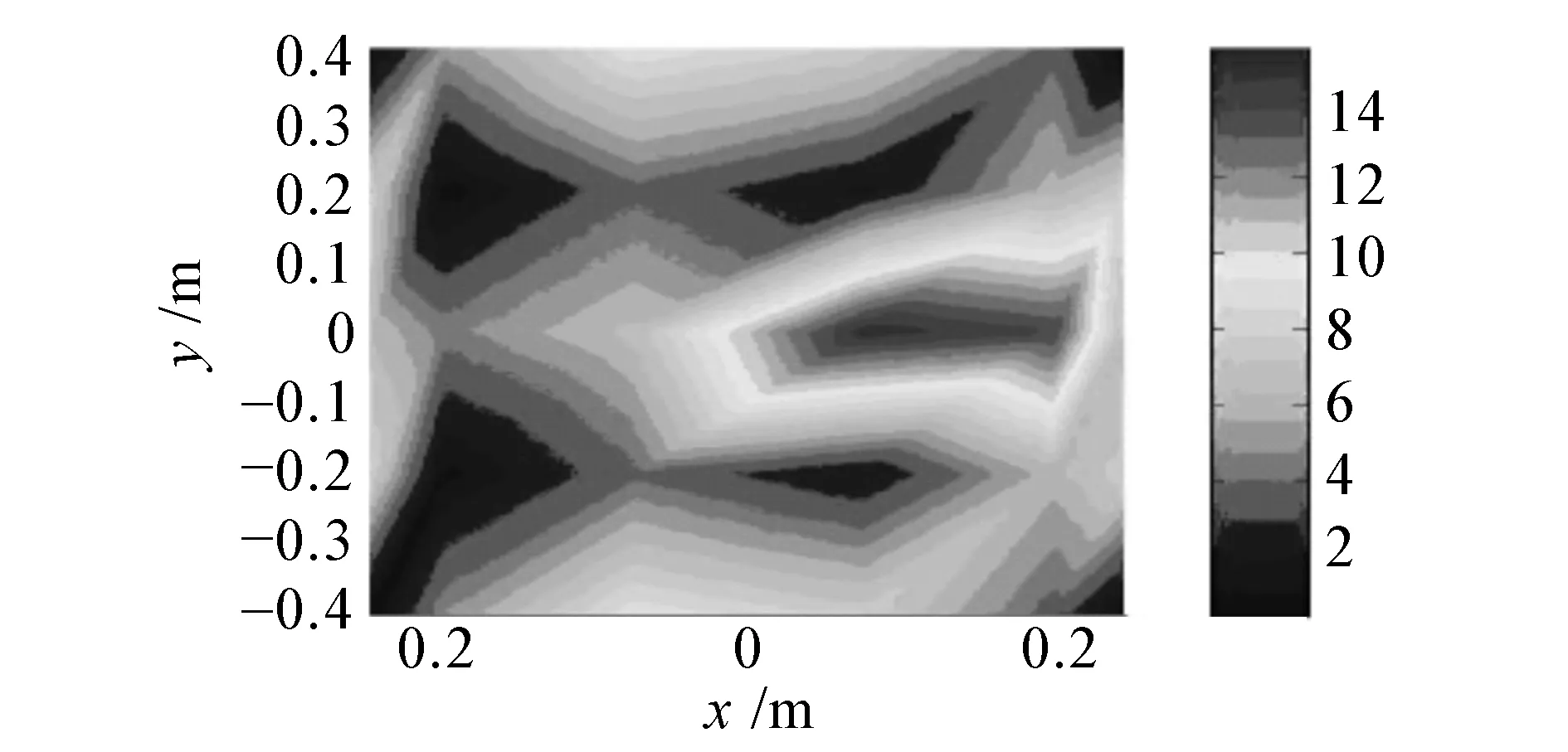
(d) 絕對硬邊界插值前聲壓幅值

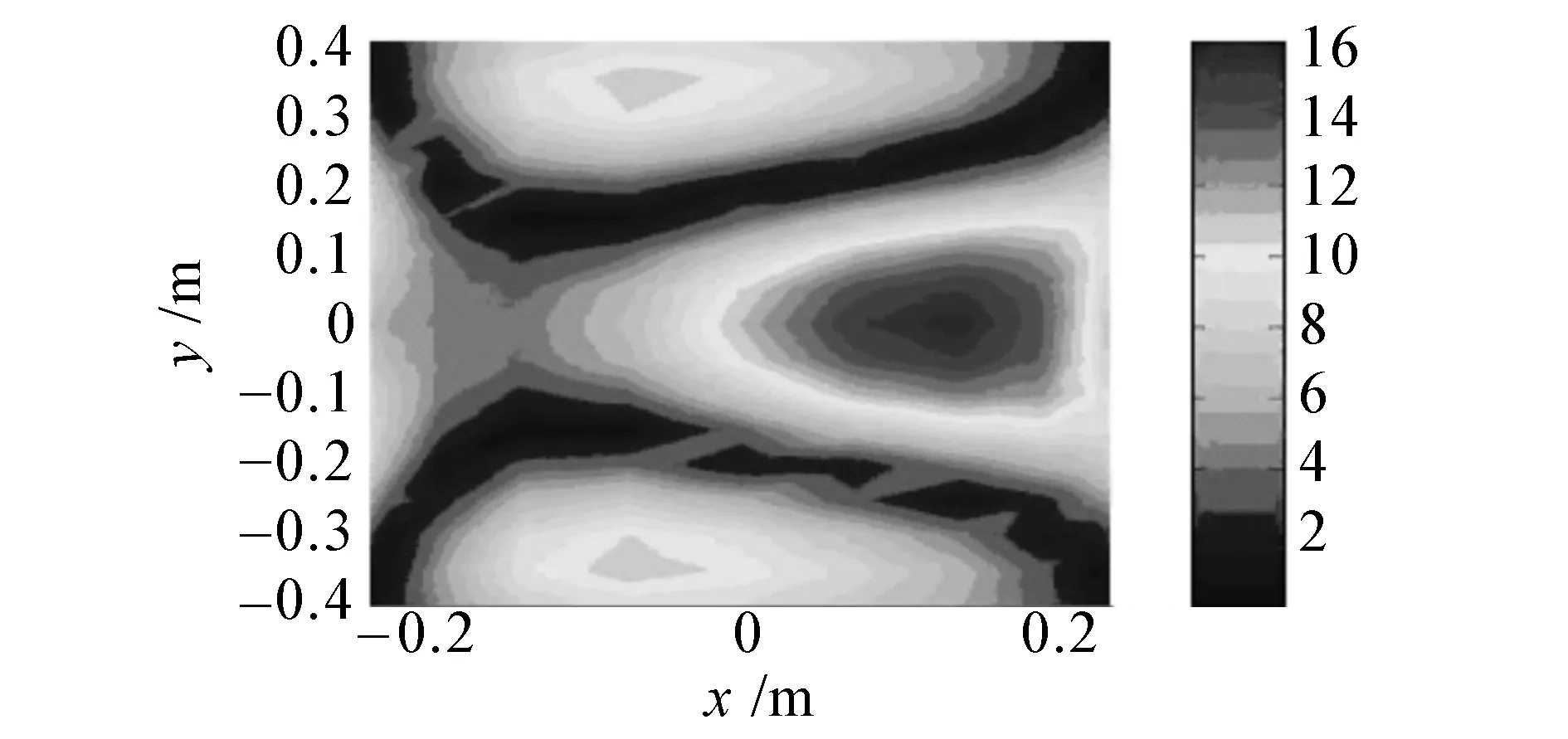
(e)絕對硬邊界理論聲壓幅值

(f) 絕對硬邊界插值后聲壓幅值

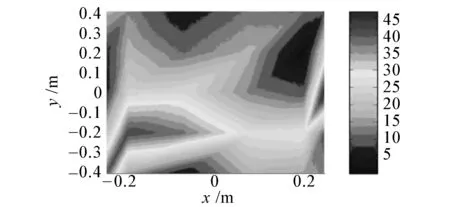
(g)絕對軟邊界插值前聲壓幅值

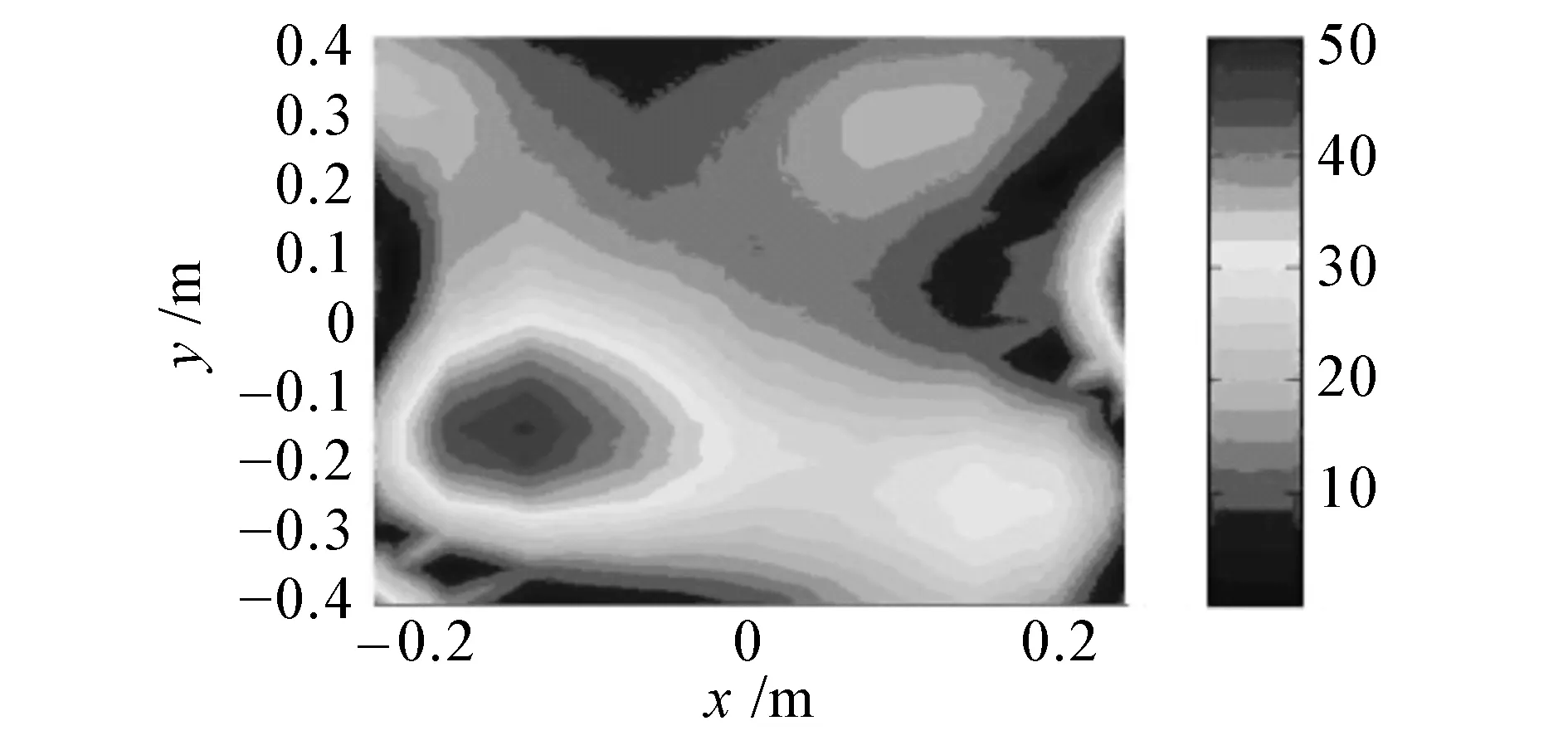
(h) 絕對軟邊界理論聲壓幅值

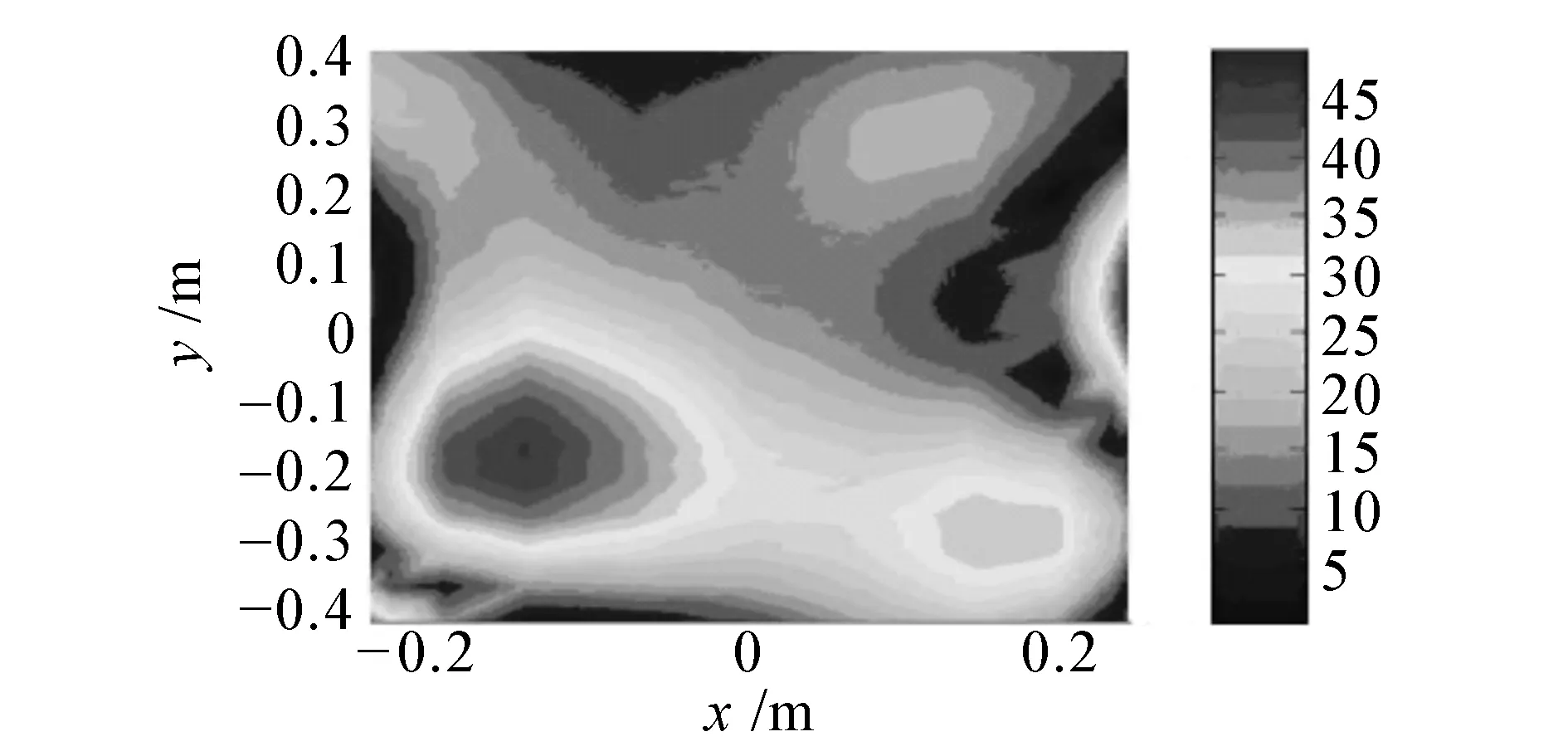
(i)絕對軟邊界插值后聲壓幅值

圖9給出了頻率在3 kHz時，測量點個數為條件4下的不同邊界條件全息面測量聲壓和插值后的聲壓及聲壓理論值的對比圖。可以明顯看出，通過插值得到了由于測點間隔較大而遺漏的聲場中的細節信息，從而有效提高了聲場的空間分辨率。

4 結論

本文通過仿真對影響外推與插值結果的參數進行了分析，利用外推或插值后的全息數據進行全息重建。通過分析得出如下結論：

1) 采用ELM技術對小孔徑測量面進行數據外推，有效地增大了測量面孔徑。將外推得到的全息面數據進行NAH重建，能夠有效提高聲場重建精度，解決了測量孔徑有限性造成的重建誤差問題。

2) 在傳感器個數較少時，采用ELM技術對全息數據進行插值，可以得到由于測點間隔較大而遺漏的聲場中的細節信息，在不增加測點數量的情況下，提高了重建圖像空間的分辨率，從而節省了工作量，提高工作效率。

3) 基于ELM的聲場插值技術除了可以將自由空間聲場進行插值外，還可應用于非自由聲場環境中，對于不同邊界條件插值效果均較好，驗證了該算法的正確性與穩健性。

參考文獻：

[1]WILLIAMS E G，MAYNARD J D，SKUDRZYK E. Sound reconstruction using a microphone array[J]. J Acoust Soc Am,1980,68(1):340-344.

[2]WILLIAMS E G，MAYNARD J D. Holographic imaging without wavelength resolution limit[J]. Phys Rev Letts,1980，45:554-557.

[3]何元安，何祚鏞．基于平面聲全息的全空間場變換：原理與算法[J]. 聲學學報,2002,27(6): 507-512.

HE Yuanan，HE Zuoyong. Full spatial transformation of sound field based on planar acoustic holography:principle and algorithm[J]. Acta Acustica,2002,27(6): 507-512.

[4]何祚鏞，何元安．近場聲全息技術應用有關物理問題研究[J]．聲學學報,2007,32(2)：137-143.

HE Zuoyong, HE Yuanan. The investigation on the physical acoustics problems of the NAH technique and its application[J].Acta Acustica,2007,32(2): 137-143.

[5]LEE M Y, BOLTON J S. Patch near-field acoustical holography in cylindrical geometry[J].J.Acoust Soc Am,2005,118(6):3721-3732.

[6]LEE M Y, BOLTON J S. A one-step patch near-field acoustical holography procedure[J].J Acoust Soc Am,2007,122(3):1662-1670.

[7]徐亮,畢傳興.基于波數域外推方法的近場聲全息[J]. 機械工程學報,2007,56(5):2776-2783.

XU Liang,BI Chuangxing. Nearfield acoustic holography based on K-space data extrapolation method[J]. Chinese Journal of Mechanical Engineering ,2007,56(5):2776-2783.

[8]徐亮,畢傳興,陳劍.基于波疊加法的Patch近場聲全息及其實驗研究[J]. 物理學報,2007,37(9):1205-1213.

XU Liang, BI Chuangxing，CHEN Jian. Algorithm and experimental investigation of patch nearfield acoustic holography based on wave superposition approach[J]. Acta Physica Sinica, 2007,37(9):1205-1213.

[9]徐亮,畢傳興.全息聲壓場的加權范數外推方法[J].物理學報,2011,60(11):114304-2-10.

XU Liang, BI Chuangxing. Hologram pressure field weighted norm extrapolation method[J]. Acta Physica Sinica, 2007,37(9):1205-1213.

[10]杜向華，朱海潮，毛榮富．基于支持向量回歸的patch 近場聲全息研究[J]. 聲學學報, 2012，37(3):286-293.

DU Xianghua,ZHU Haichao,MAO Rongfu.Patch near-field acoustic holography based on support vector regression[J]. Acta Acoustica,2012,37(3):286-293.

[11]張小正,畢傳興,徐亮.基于波疊加法的近場聲全息空間分辨率增強方法[J]. 物理學報,2010,59(08):5564-5570.

ZHANG Xiaozheng,BI Chuanxing,XU Liang.Resolution enhancement of nearfield acoustic holography by the wave superposition approach[J]. Acta Physica Sinica, 2010,59(8):5564-5570.

[12]毛榮富，朱海潮．近場聲全息中減少測量點數的研究[J].聲學技術,2009,28(3):287-294.

MAO Rongfu, ZHU Haichao. A study of measurement point reduction in near-field acoustic holography[J].Technical Acoustics,2009,28(3):287-294.

[13]HUANG G B. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems, Man and Cybernetics—Part B: Cybernetics, 2012,42(2),513-529.

[14]HUANG G B, SIEW, C K. Extreme learning machine with randomly assigned RBF kernels[J]. International Journal of Information Technology, 2005,11(1):16-24.

[15]HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine: theory and applications[J]. Neurocomputing, 2006,70: 489-501.