大型飛機顫振試飛低頻密集模態參數辨識

盧 曉 東

(中國飛行試驗研究院 飛機所, 陜西 西安 710089)

0 引言

按照GJB67.7A-2008以及CCAR-25-R4[1]的要求,新機定型試飛或合格審定試飛必須進行顫振飛行試驗,確保新機的各種構型在其整個飛行包線范圍內都不會發生顫振現象。在新型或改型飛機的研制過程中,飛機顫振飛行試驗是必須進行的試驗項目,其目的在于確定相應的顫振特性,包括顫振類型、模態參數及顫振邊界。

傳統的飛行包線擴展試驗主要采用的是亞臨界方法,并不是飛到顫振速度。該方法的基本思路是:對選定的每一種試驗構型,分別在不同的飛行高度和速度下對飛機進行激勵,并記錄飛機結構對激勵的響應。通過對這些響應的計算分析,求出若干個感興趣的結構模態的頻率和阻尼。根據這些模態頻率和阻尼隨速度(或速壓)的變化規律進行工程外推,來預測飛機的顫振臨界速度[2]。因而模態參數識別是其中最主要的一個環節。

多年來,研究人員已發展了相當數量的模態參數識別方法,包含時域、頻域甚至時頻域方法。時域和時頻域方法[3]在速度上不能很好地滿足顫振試飛的要求,因此主要采用的是頻域方法,如正交多項式方法[4-5]。針對大型飛機頻率低且密集的特點,本文提出了將主分量分析的模態參數辨識方法[6-8]引入飛機的顫振特性試飛數據處理領域。文中首先介紹了該方法的理論基礎,然后通過仿真數據和試飛數據對該方法進行了驗證和應用分析。分析結果表明,該方法是一種極具實用價值的模態參數辨識技術。

1 理論基礎

對一個l輸入m輸出的n自由度線性系統,其脈沖響應函數矩陣P(t)∈Rm×l可以用模態參數來表示:

P(t)=ΦeΛtΓT

式中,Φ∈Cm×l為振型矩陣;Λ∈C2n×2n為特征值對角矩陣;Γ∈Cl×2n為模態參與矩陣。這里Φ,Λ,Γ均是共軛成對的。

對上式進行Laplace變換,則可以得到頻率響應函數矩陣為:

H(s)=L(P(t))=Φ[sI-Λ]-1ΓT

頻率響應函數矩陣由正共軛和負共軛兩部分組成,負共軛部分相對于正共軛部分很小,因此可以將其近似為一常數矩陣。另外,考慮分析頻段外剩余模態的影響,亦可近似為另一常數矩陣。故上式可以改寫成:

對脈沖響應函數矩陣求導,即可得到頻響函數矩陣、常數矩陣、脈沖響應函數的初始狀態矩陣、振型矩陣、極點矩陣以及模態參與矩陣之間的關系式:

必然存在一個系統矩陣A∈Cm×m,滿足特征值問題:

AΦn=ΦnΛn

將方程進一步簡化得到:

式中,Il為l維的單位矩陣。

在分析頻段內的各離散頻率點ωi(i=1,2,…,L)處,上式均可成立,聯立求解可得到系統矩陣A以及常數矩陣K。而系統的模態參數可以通過求解A的特征值問題來獲得。

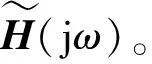
主分量的階次n即為該分析頻段內的有效模態數,亦即該分析頻段內的系統階次。可以看到,該方法是典型的多輸入多輸出參數識別方法,具備識別密集模態的能力;由于考慮了帶外模態的影響,低頻模態識別更加準確;通過采用主分量分析技術,數據量得到了極大壓縮,保證了運算速度。因而,本文所提方法非常適用于大型飛機的顫振試飛數據處理。

2 仿真算例分析

為了驗證該模態參數辨識方法的正確性和有效性,設計一個三自由度的彈簧質量系統,該系統具有三階低頻密集模態,其理論模態參數如表1所示。

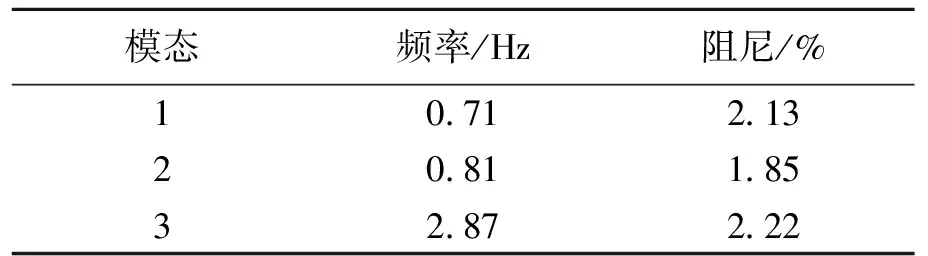
表1 三自由度系統理論模態參數Table 1 Theoretical modal parameters of a three-degrees of freedom system

利用上述模態參數仿真產生三自由度系統的頻率響應函數,添加20%的噪聲,其中白色噪聲和有色噪聲各半。仿真頻率響應函數的頻率分辨率為0.01 Hz,譜線數為400線,頻率范圍為0.01～4.00 Hz。在識別過程中分別選擇兩個頻段進行識別,第一個頻段包含第一、第二階模態,第二個頻段則只包含第三階模態。頻響函數及其擬合曲線如圖1和圖2所示。

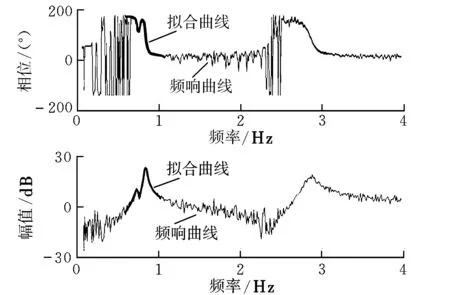
圖1 第一階和第二階模態頻響函數及其擬合曲線Fig.1 Frequency response function and fitted curve of the first and the second modes

圖2 第三階模態頻響函數及其擬合曲線Fig.2 Frequency response function and fitted curve of the third mode

表2給出了采用基于主分量分析的模態參數辨識方法所識別的三階模態結果。通過與理論值對比可知,識別算法正確,在數據存在較大噪聲的情況下,其模態頻率和阻尼的識別結果誤差較小,能夠滿足顫振試飛數據處理的需求。

表2 三自由度系統模態參數識別結果Table 2 Identified model parameters of a three-degrees of freedom system

3 試飛數據分析

為了驗證該方法在顫振試飛中的實際使用效果,對典型實測的飛行顫振試驗數據進行分析。該數據為利用1～15 Hz的操縱面掃頻激勵方法對飛機結構進行激勵,測量得到的飛機機翼尖部結構響應。響應信號的采樣率為256 Hz,分析數據的樣本長度為30 s,獲得的頻率響應函數如圖3所示。從圖3中可以看出,該飛機結構模態頻率很低且十分密集,5 Hz以下至少包含5階模態。

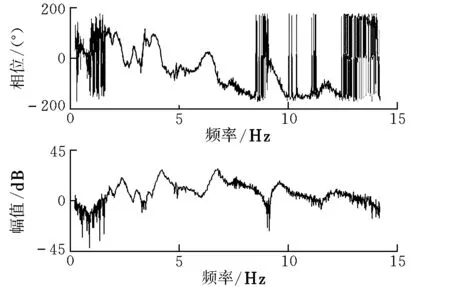
圖3 典型的實測數據頻響函數曲線Fig.3 Frequency response function of real data

應用基于主分量分析的模態參數識別技術對上述實測的頻響函數進行分析,識別出3階主要結構模態,分析結果如表3所示。

由表3可以看出,識別出了飛機結構的主要3階低頻密集模態,而且識別出的模態參數結果合理,說明該方法能夠適用于顫振試飛數據處理。另外,由于該方法可以進行總體一次性識別,計算量遠小于傳統的模態參數識別方法,因此能夠大大提高試飛數據處理的效率。

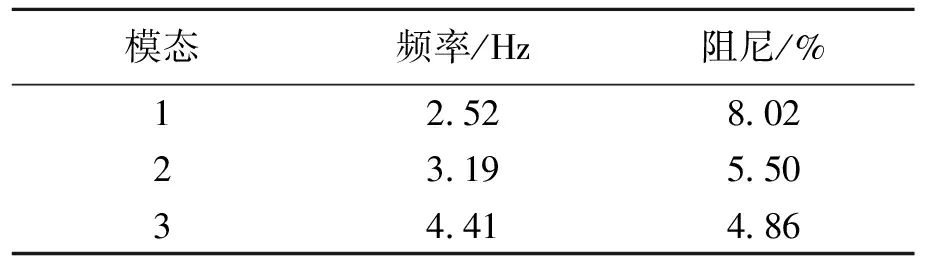
表3 典型的實測數據識別結果Table 3 Identified results from the real data

4 結論

(1)對一個三自由度具有低頻密集模態的彈簧質量系統的仿真分析表明,各階模態頻率識別結果與理論結果一致,模態阻尼誤差在0.1%以內,表明主分量分析方法可有效識別低頻密集模態參數。

(2)通過飛機實測響應數據的分析表明,主分量分析方法識別的結果可靠,適用于大型飛機顫振試飛中的低頻密集模態參數辨識。

(3)主分量分析方法能夠顯著減小模態參數識別的計算量,提高試飛數據處理的效率,滿足飛機顫振試飛實時監控/處理工程技術需求。

參考文獻：

[1] 中國民用航空局.CCAR-25-R4 運輸類飛機適航標準[S].北京:中國民用航空局,2011.

[2] 管德.飛機氣動彈性力學手冊[M].北京:航空工業出版社,1994:254-267.

[3] Martin J B.Wavelet analysis of F/A-18 aeroelastic and aeroservoelastic flight test data[R].NASA-TM 4793,1997.

[4] Richardson M H.Global frequency & damping estimates from frequency response measurements [C]//Society for Experimental Mechanics Proceedings of the 4th International Modal Analysis Conference.New York,USA:Union College,1986:465-470.

[5] 王彤,張令彌.有理分式正交多項式頻響函數模態參數識別[J].航空學報,2003,24(2):140-143.

[6] Zhang L M,Kanda H,Brown D L,et al.A polyreference frequency domain method for modal parameter identification [Z].New York,USA:American Society of Mechanical Engineers,1985.

[7] 傅志方.振動模態分析與參數辨識[M].北京:機械工業出版社,1990.

[8] 王彤.復雜結構多輸入多輸出頻域模態參數識別研究及軟件實現[D].南京:南京航空航天大學,2003.