基于馬爾可夫模型的城鄉結合部地價規律研究
——以北京市為例

郭莉濱

(重慶第二師范學院，重慶 400065)

馬爾可夫模型是地理預測中常用的重要方法之一[1]，主要是根據事件的目前狀況對未來各時期可能出現的變化情況進行預測，基本立足點是馬爾可夫鏈。顯而易見的是，雖然地價在空間上表現一定的規律性，但仍然會受到許多不確定性因素的影響，從而使地價在空間上也呈現出不確定性。影響的主要因素，包括土地的供需關系、土地需求者對不動產市場的心理預期，以及干擾因素的存在，甚至于某些偶然因素，等等。傳統地價指數編制的高難度和信息的滯后性，以及常用預測方法忽視地價指數隨時間變化呈現上漲趨勢的非平穩隨機過程，極易造成預測精度低等問題[2]。本文嘗試為城鎮地價指數提供一種全新的預測方法，即運用隨機過程中馬爾可夫鏈理論，構建起地價預測模型，進而對地價的空間變化特征進行定量分析，由此推算出在城市擴展過程中，距城市中心不同距離的城鄉結合部的不同地價，以此為農地分等定級估價以及征地片區綜合地價制訂等提供理論依據[3]。

1 馬爾可夫模型的基本原理

1.1 計算地價狀態轉移概率矩陣

一般而言，地價狀態轉移概率，是指在由于區位不同導致的地價變化中，在某一區位處于某一種地價的狀態下，其下一個區位出現有別于上一區位地價的可能性。按照對條件概率的界定，如果地價狀態Ei轉為狀態Ej，那么狀態轉移概率Q(Ei→Ej)就是條件概率Q(Ej/Ei)，即

Q(Ei→Ej)=Q(Ei/Ej)=Qij

(1)

我們假定地價狀態轉移概率矩陣在某一方向沿線上被預測的地價可能狀態有E1，E2，E3，…，En。那么，從地價狀態Ei轉為狀態Ej的狀態轉移概率，記為Qij，并形成矩陣[3]：

(2)

把地價的狀態轉移概率矩陣記為Q。假定在被預測的某一方向沿線上，某一點的目前狀態為Ei，那么在距其一定距離的下一點，則有可能轉為E1，E2，…Ei，…En中的任一狀態。基于此，Qij應當滿足以下條件：

(3)

一般地，我們把滿足(3)式的矩陣，稱為隨機矩陣或概率矩陣。容易證明，如果Q為概率矩陣，那么對于任何數，只要m>0，Qm都是概率矩陣。如果Q為概率矩陣，而且存在整數m>0，使得Qm中的各元素全部不是零，則把Q稱為標準概率矩陣。

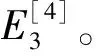
1.2 計算北京市京密引水渠沿線地價變化的狀態轉移概率矩陣

選取北京市城鄉結合部京密引水渠方向上的地價作為例子探討。基礎數據來源于課題組的實地調查。

首先，表1給出了北京市京密引水渠沿線等間距(間距為0.3km，由于實地情況的限制，間距誤差在5%之內)共36個調查點地價狀態的變化情況，方向為偏離市中心方向。

表1 北京市京密引水渠沿線等間距地價狀態變化情況

再計算地價變化的狀態轉移概率矩陣。根據表1數據，有

Q11=Q(E1→E1)=Q(E1/E1)=5/13=0.2000

Q12=Q(E1→E2)=Q(E1/E2)=7/15=0.4667

Q13=Q(E1→E3)=Q(E1/E3)=4/11=0.3333

Q21=Q(E2→E1)=Q(E1/E2)=7/13=0.5385

Q22=Q(E2→E2)=Q(E2/E2)=2/13=0.1538

Q23=Q(E2→E3)=Q(E3/E2)=4/13=0.3077

Q31=Q(E3→E1)=Q(E1/E3)=4/11=0.3636

Q32=Q(E3→E2)=Q(E2/E3)=5/11=0.4545

Q33=Q(E3→E3)=Q(E3/E3)=2/11=0.18181

則京密引水渠方向地價變化的狀態轉移概率矩陣為

(4)

2 馬爾可夫模型的應用

2.1 預測地價

運用上述模型，可以預測該方向上更遠距離的地價水平。

我們首先假定狀態概率為πj(g)，也就是事件在初始狀態(g=0)為已知的條件下，經過g次狀態轉移，在第g個時刻處于狀態Ej的概率。按照概率的性質，可得

(5)

可以看到，從初始狀態開始，經g次狀態轉移到達狀態Ej的這一過程，可視為首先經過(g-1)次狀態轉移到達狀態Ei(i=1，2，…，n)，然后再經過一次狀態轉移，從狀態Ei到達Ej。根據馬爾可夫過程的無后效性和Bayes條件概率公式，可以得到

(6)

若行向量π(g)=[π1(g)，π2(g)，…，πn(g)]，則由(6)式得出逐次計算狀態概率的遞推公式

(7)

在(7)式中，π(0)=[π1(0)，π2(0)，…，πn(0)]，為初始狀態概率向量。

可以運用以上結果對京密引水渠方向上的地價進行預測。如果將第36個樣點的地價變化狀態記為π(0)=[0，1，0]，就可以把地價狀態轉移概率矩陣及π(0)代入遞推公式，得出這一方向上沿線地區可能出現的地價變化狀態的概率(表2)。

表2 京密引水渠沿線地區地價變化狀態預測表

注：表中“距離”是根據北京市城市擴展情況，通過幾何計算確定的中心點距樣本點之間的距離。

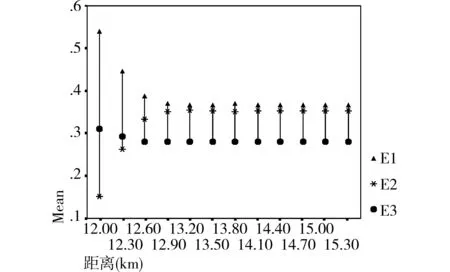
圖1 京密引水渠沿線地區地價變化狀態垂線圖

根據上述數據繪制京密引水渠方向地價變化垂線圖(圖1)。從圖中可以看出，E1、E2、E3隨著距離的增加有很大變化，在一定距離之后，變化則逐漸減小。在三個指標之中，E1變化幅度最為激烈，E3變化幅度最小。由此可見，在該方向沿線上，地價下降趨勢較為明顯，但在一定因素作用下，某些區位的地價卻能夠保持在一定的水平上，甚至高出離城區更近的區位地價。

2.2 預測地價的總體趨勢

我們把經過無窮次狀態轉移后得到的狀態概率，稱為“終極狀態概率”或“平衡狀態概率”。如果把“終極狀態概率”向量記為π=[π1，π2，…，πn]，那么

(8)

即

(9)

按照極限的定義，可知

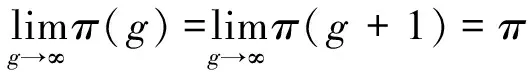
(10)

將其代入馬爾可夫預測模型的遞推公式，得到：

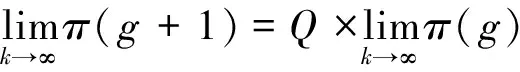
(11)

由此，可以得到終極狀態概率應滿足的條件：

A.π=πQ

B. 0≤πi≤1(i=1，2，…，n)

在三個條件中，B、C是狀態概率的要求，其中B表征的是，在經過無窮次狀態轉移后，該事件仍處于n種狀態中的一種。條件A用于計算終極狀態概率，是預測馬爾可夫過程可能出現某種趨勢的重要信息。

根據上面的方法計算京密引水渠方向地價變化終極狀態概率，設該概率為π=[π1，π2，π3]，則

[π1，π2，π3]=

(12)

即

(13)

求解方程組，得

π1=0.4653，π2=0.3525，π3=0.1822。

結果表明，在京密引水渠方向沿線地區，隨著距中心城區距離越遠，地價總體水平呈下降趨勢，上升趨勢概率約為18.22%。

2.3 對比不同區域

運用上述方法，結合課題組調研的數據資料，分別從北京市5個方向上(西北、東北、正東、東南、西南)對城鄉結合部地價趨勢進行預測，結果見表3和圖2。

表3 北京市5個方向上城鄉結合部地價趨勢預測

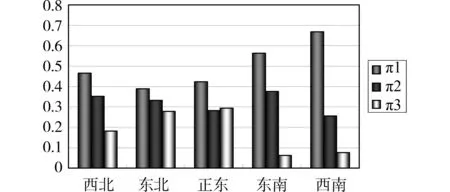
圖2 北京市5個方向上城鄉結合部地價趨勢比較圖

以上結果顯示，北京市5個方向上的地價變化趨勢存在很大差異，這也從一個側面印證了北京市的不均衡發展。結果表明，北京市西南方向地價下降趨勢最為明顯，東南方向次之。地價變化幅度最小的是東北方向。結合北京市道路網絡圖(圖3)，可以看出，北京市的不均衡發展在很大程度上影響了城鄉結合部的地價分布規律，由于投入不足，交通網絡不發達，市政基礎設施不完善，使得西南和東南方向的地價在偏離中心城區一定距離后陡降；對其他幾個方向而言，在偏離中心城區一定距離內，仍具有發達的交通網絡和基礎設施，地價自然下降得不大。

圖3 北京市道路網絡圖

同時，在各個方向上一些衛星城鎮對地價的影響也很大。從北京市衛星城鎮體系圖(圖4)可以看出，西北、東北、正東方向皆有兩個左右的衛星城鎮，基于城市引力模型，這些城鎮對于該方向上的市場結構和發展形態產生作用，進而影響到地價的變化規律。而這種影響程度的大小取決于衛星城鎮的人口數量。對于西南和東南方向而言，由于衛星城鎮的數量較少甚至沒有，因此，衛星城鎮對于地價的提升作用就不明顯。這樣，就會出現隨著距市區距離越遠，地價越低的局面[5]。

圖4 北京市衛星城鎮體系圖

3 結果討論

農用地的轉用過程集中發生在城鄉結合部，伴隨著土地權屬的變更和使用方式的演替，作為其轉換價值表象的地價必然會發生變化。因此，在城鄉結合部，地價的變化規律迥異于城市內部。研究農地轉用價格，通過城鄉結合部這一載體，可以更深入地了解農地的價值構成以及不同因素對于地價的影響。選用一定的定量模型，即可達成上述目的[6]。通過運用Margov模型對北京市城鄉結合部的地價進行測算，結果顯示，上述模型可以在一定程度上反映出北京城鄉結合部地價的變化規律，為進一步認識土地在城市化過程中的價格規律奠定了基礎。其模型的測算結果，可以反映出以下問題：

3.1 北京城市發展的不均衡性

任何一種經濟活動都處于從均衡到不均衡、再到均衡的演變過程中。經濟發展與城市化具有一致性，初期總是先在空間的某一點上形成一個發展極，人口、技術、資本都向這個點集聚，然后再通過產品的交易過程實現向周邊的擴散[7]。集聚與擴散的過程，使得區域經濟發展呈現從點到線、再連線成網、從網到片的趨勢。城市化的過程，就是這樣一種不均衡發展的過程。北京的城市發展印證了這一點。通過兩個模型的測算結果，可以清晰地看出，北京市城市處于不均衡的發展過程中，具體表現在城鄉結合部地價變化的規律上。由于基礎設施、各種投入的差異，甚至還有人們傳統思維中“北貴南賤”的思想，北京的城北地區在發展過程中逐步形成了很大的既得優勢，積累了大量物質要素，這無形中提高了人們對于城北地區的期望[8]。這也造成了城北地區農地轉用價格明顯高于其他方位的現象。造成這種現象的深層次原因，還是農地價格構成中的未來價值增長部分的差異。在區位因素、基礎設施、環境條件乃至個人偏好等因素的綜合作用下，對于城北地區未來價值增長的預期明顯高于其他方向的相應區域，于是，地價的變化也就清晰地反映出了這種差異[9]。因此，一個城市的發展應該是均衡或者是相對均衡的，否則城市的發展是難以可持續的，城市的蔓延也是無規則、非精明的。要改變北京城市發展的不均衡性，將是一項長期的工作，除了通過加大投入來提升土地價值之外，改變人們的觀念也是需要做的工作[10]。

3.2 影響城鄉結合部地價變化的多因素性

城市地價受多種因素影響，而且在這些因素作用下呈現出一系列的變化規律。城鄉結合部農地轉用價格的情況，較城市地價更加復雜，受到更多因素的影響。影響農地未來價值增長的因素，既有宏觀因素，也有微觀因素。從宏觀因素看，包括城市化進程、城市發展政策、投資趨向以及資本市場等。從微觀因素看，又可分為實體因素和虛幻因素。實體因素包括基礎設施、環境條件等，虛幻因素是人們對于農地轉用后基于該地塊的預期，其又受到傳統思維、個人偏好、社會導向等因素影響。以上分析可以看出，正是這些因素的綜合作用，才形成了模型測算出的北京市城鄉結合部不同方向上地價變化規律的迥異狀況[11]。因此，進一步對這些影響因素進行分析，對于我們深入認識農地轉用價格有重要的意義。

參考文獻：

[1]彭俊，陳方正.城市土地價格的靜態守恒與動態增長特征研究[J].同濟大學學報(自然科學版)，2005，(6)：838-842.

[2]陳順強，馬嘿瑪伙.基于隱馬爾科夫模型的彝文分詞系統設計與開發[J].西南民族大學學報(自然科學版)，2012，38(1)：146-149.

[3]阿瑟·奧沙利文.城市經濟學[M].北京：中信出版社，2002.

[4]劉俊，田崇新，張小燕，鄭光輝.馬爾可夫鏈在地價預測模型中的應用研究[J].南京師大學報(自然科學版)，2005，(03).

[5]梅昀，陳銀蓉，胡偉艷.農用土地的價值觀與農地轉用價格評估[J].國土資源科技管理，2004，(5)：26-29.

[6]陳思源，曲福田.GIS空間分析支持下的城市地價分布研究——以江蘇省鎮江市為例[J].南京農業大學學報，2005，28，(3)：119-122.

[7]謝文蕙.城市經濟學[M].北京：清華大學出版社，1996.

[8]王霞，朱道林.地統計學在都市房價空間分布規律研究中的應用——以北京市為例[J].中國軟科學，2004，(8).

[9]張新長，梁金成.城市土地利用動態變化及預測模型分析[J].中山大學學報(自然科學版)，2004，(3)：121-125.

[10]李亞麗，左獻娟，秦耀辰.基于CA的鄭州市土地利用演化研究[J].華北水利水電學院學報，2011，(10)：31-34.

[11]胡希軍，胡伏湘，何平，沈守云.基于馬爾可夫鏈的城市景觀結構演化模擬及預測[J].武漢大學學報(信息科學版)，2009，(10).