基于自適應閾值的腦電信號去噪方法*

馬玉良,許明珍,佘青山,高云園,孫 曜,楊家強

(1.杭州電子科技大學智能控制與機器人研究所,杭州 310018;2.浙江大學電氣工程學院,杭州 310027)

?

基于自適應閾值的腦電信號去噪方法*

馬玉良1,許明珍1,佘青山1,高云園1,孫 曜1,楊家強2*

(1.杭州電子科技大學智能控制與機器人研究所,杭州 310018;2.浙江大學電氣工程學院,杭州 310027)

腦電采集后得到的腦電信號(Electroencephalogram,EEG)中含有噪聲信號,為了有效去除噪聲并保留有用信息,本文在軟閾值去噪的基礎上,提出一種改進閾值去除EEG噪聲的算法。利用小波變換對EEG信號分解,得到多層的高頻系數和低頻系數;根據分解層次不同,對小波系數進行自適應的閾值處理;將縮放后的小波系數重構,得到去噪后的EEG信號。以信噪比、均方根誤差作為去噪效果的定量指標,將改進算法與硬閾值法、軟閾值法、Garrote閾值法進行比較,結果表明,改進閾值法優于其他3種閾值法。

腦電信號;自適應閾值;信噪比(SNR);均方根誤差(RMSE)

大腦是有億萬個神經元組成的復雜系統,負責人體的各個功能的協調運作,通過大腦皮層上的電極記錄下大腦細胞群的電位活動稱為腦電信號EEG(Electroencephalogram)。通過對EEG的分析研究,可以獲得豐富的的生理、心理以及病理信息,是臨床醫學和大腦研究領域的一個重要工具[1-2]。然而EEG又是一種隨機性很強的非線性非平穩信號,而且信號強度非常微弱,在采集和處理過程中,極易受到高斯噪聲信號的干擾,嚴重影響信號的分析研究工作[3]。因此去噪在腦電研究過程中扮演著重要的角色,去噪效果的好壞直接影響腦電信號特征提取和分類的效果。

小波變換是傅里葉變換的繼承和發展,具有時頻局部化、多分辨率和去相關性的特點,很適合探測信號的瞬時狀態,對微弱的信號可以進行有效去噪[4]。小波變換可以提取出不同頻段的小波系數,對高頻段和低頻段的小波系數置零或進行小波閾值處理,將高斯噪聲去除,到達去噪的目的。小波閾值濾波方法是目前常用的一種閾值去噪方法,基于小波閾值的信號去噪,其算法簡單,計算量少,在保持信號奇異性的同時能有效的濾除噪聲,被廣泛的應用到腦電去噪領域[5-6]。但傳統的硬閾值法和軟閾值法在消噪方面都存在缺陷,如硬閾值去噪過程中因斷點而造成的局部震蕩,軟閾值去噪后丟失奇異點信息等[7-8]。

由于選取不同的閾值和不同的閾值函數將直接影響到最后去噪的效果,本文在軟閾值處理的基礎上,提出自適應閾值處理的EEG去噪方法,實驗表明,該算法去除腦電信號中的噪聲效果較好,與傳統的閾值濾波去噪方法比較能進一步提高信號的信噪比,減少均方根誤差。

1 小波閾值去噪

1994年Donoho提出了硬閾值和軟閾值去噪的方法,被廣泛的應用到各個領域。小波閾值去噪基本思想:選取適當的小波函數族,對含噪信號進行小波分解,將噪聲信號分解到不同的子頻帶上,即得到近似系數和細節系數。通常噪聲信號為高頻信號,因此設定適當的閾值對小波系數進行處理,濾除噪聲信號,保留有用的信號系數,從而達到去噪的目的。

常用的閾值函數有硬閾值函數[9],軟閾值函數[10],Garrote閾值函數[11],其中硬閾值函數的數學表達式為

(1)

軟閾值處理的數學表達式為

(2)

Garrote閾值處理數學表達式為

(3)

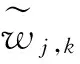
2 改進閾值去噪方法

由于硬、軟閾值在去噪方面都有缺陷,為了使EEG信號在去除噪聲干擾的同時能保存更多的有用信息。本文在軟閾值的基礎上進行了改進,在連續性更好的同時,偏差小于單純的軟閾值去噪[12]。其數學表達式如下:

(4)

式中,a為形狀系數,用于控制wj,k<λj,k區域內函數的形狀,即控制衰減程度。從表達式(4)可以得出,當a=0時,該方法是軟閾值法,在a為非0情況下,改進的閾值函數比純軟閾值函數更具有平滑性。

假設有一采樣EEG信號,記為:

x(t)=s(t)+e(t),t=0,…,N-1

(5)

其中x(t)為含噪EEG信號;s(t)為真實EEG信號;e(t)為噪聲信號,通常表現為高頻信號。本文提出一種改進軟閾值去噪方法用于腦電信號的去噪,主要的去噪步驟如下:

(1)選取合適的小波函數,確定小波分解層數j,將EEG信號進行小波分解至j層,得到相應的分解系數wj,k。

(2)計算各個分解子空間的Donoho閾值,記為λj,k,這是小波閾值算法的關鍵,要選取閾值函數和合適的閾值。

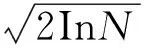
(6)

其中N是相應層的小波變換系數的個數。

由于Donoho閾值去噪后得到的信號過于平滑,容易失去原始信號信息。本文在Donoho閾值的基礎上改進閾值函數,定義加權閾值縮放因子λj為:

λj=p/(1+In(j))2

(7)

其中,p≥0、j是分解尺度。

對Donoho閾值進行縮放得到各個分解子空間的閾值,記為Tj,k:

Tj,k=λj*λj,k

(8)

根據每層采用不同的閾值的特點,當頻率相對高時,需要對高頻部分子空間的閾值進行放大,當頻率相對低時,需要對低頻子空間的閾值進行縮小,進而增強對EEG中高頻噪聲的抑制,保留低頻有用信號。

(3)將低頻系數和處理后的高頻系數進行重構,得到消噪后的EEG信號。

3 實驗模式和數據采集

實驗EEG數據采用2003年腦-機接口(BCI)競賽的公開數據,此數據是由奧地利格拉茲工業大學BCI研究中心提供。

實驗數據來自于一名25歲的女性,根據顯示屏上的左右方向鍵提示,受試者想象左右手運動,分別從C3,C4,和Cz3個電極處取得腦電信號。按照國際標準10-20系統,以左側乳突為參考電極,右側乳突為接地電極,電極安放位置如圖1所示,數據采集實驗示意圖如圖2所示。

實驗過程:受試者靜坐在扶椅上注視顯示器,每次試驗持續9 s,在t=0～2 s過程中,受試者處于安靜狀態,不做任何思維想象;t=2 s時,計算機會發出一聲提示音,同時顯示器中央出現一個“+”,持續1 s,提示受試者做好準備;在t=3 s時候,顯示器上開始隨機出現指示左或者右的箭頭,受試者根據箭頭的指向,想象左手、右手運動,一直到第9 s試驗完成。所有試驗由7組組成,每組實驗進行40次,每次實驗持續時間9 s,共進行280次試驗,選取140次用來訓練分類器,另外140次用來測試分類器。本文選取140次訓練分類器數據中C3通道EEG進行去噪試驗,圖3是實驗采集到的其中一段C3通道腦電信號。

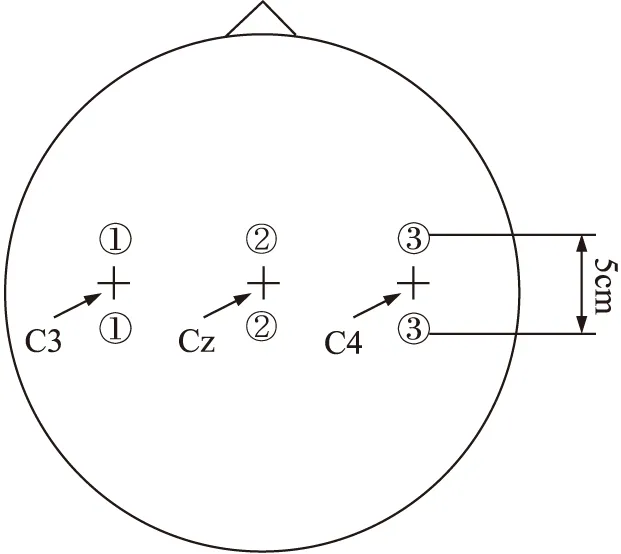
圖1 電極放置位置圖

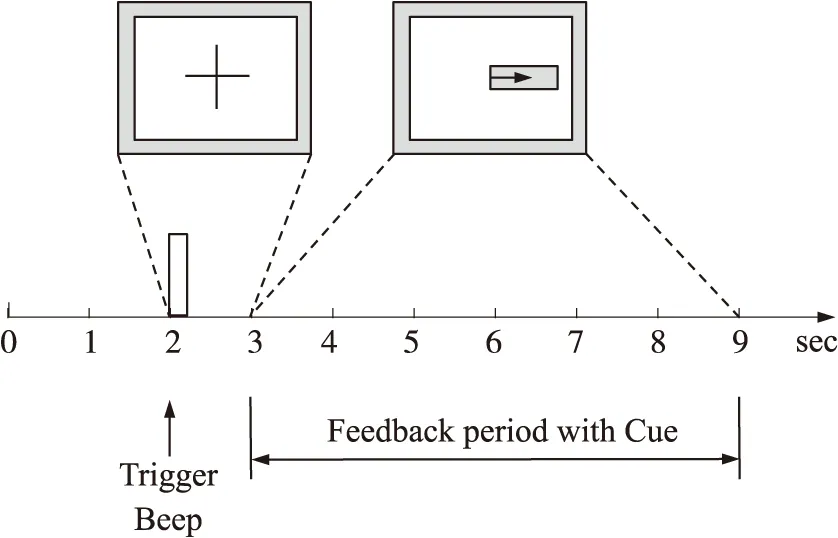
圖2 數據采集實驗示意圖

圖3 原始C3通道的EEG信號

4 實驗結果及分析

為了證明改進閾值法在EEG信號去噪方面的有效性,在MATLAB2012b平臺上,對140次測試數據依次進行閾值去噪處理。為了定量的分析改進算法的優越性,本文采用信噪比(SNR)和均方根誤差(RMSE)兩個評價指標來檢驗改進閾值算法的優于其他3種閾值去噪算法,其定義分別為:

(9)

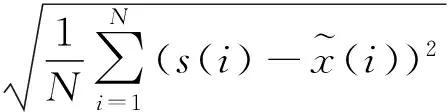
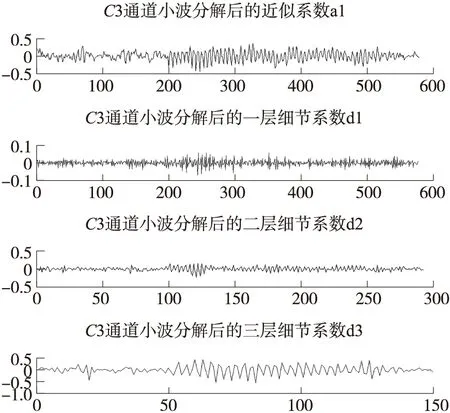
圖5 C3通道信號進行3層小波分解后的近似系數和細節系數

(10)

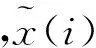
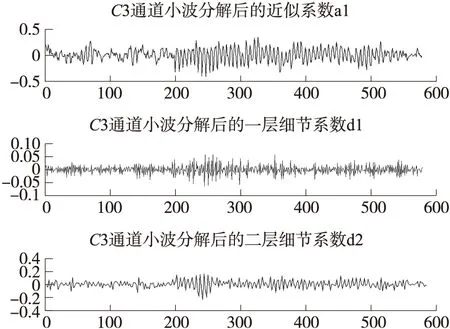
圖4 C3通道信號進行2層小波分解后近似系數和細節系數

表1 3層分解時不同算法去噪效果的SNR和RMSE結果對比

表2 取不同的a和p的值,對SNR和RMSE的影響

如表2所示,在a值一定的時候,隨著p的值增大,SNR和RMSE的值不斷減小;當p值不變的時候,隨著a的取值不斷增大,SNR和RMSE的取值不斷減小,所以改進閾值算法中當a=0.01,p=0.1時,去噪后的效果最為理想。圖6為C3通道EEG信號進過各個閾值去噪后的效果圖。

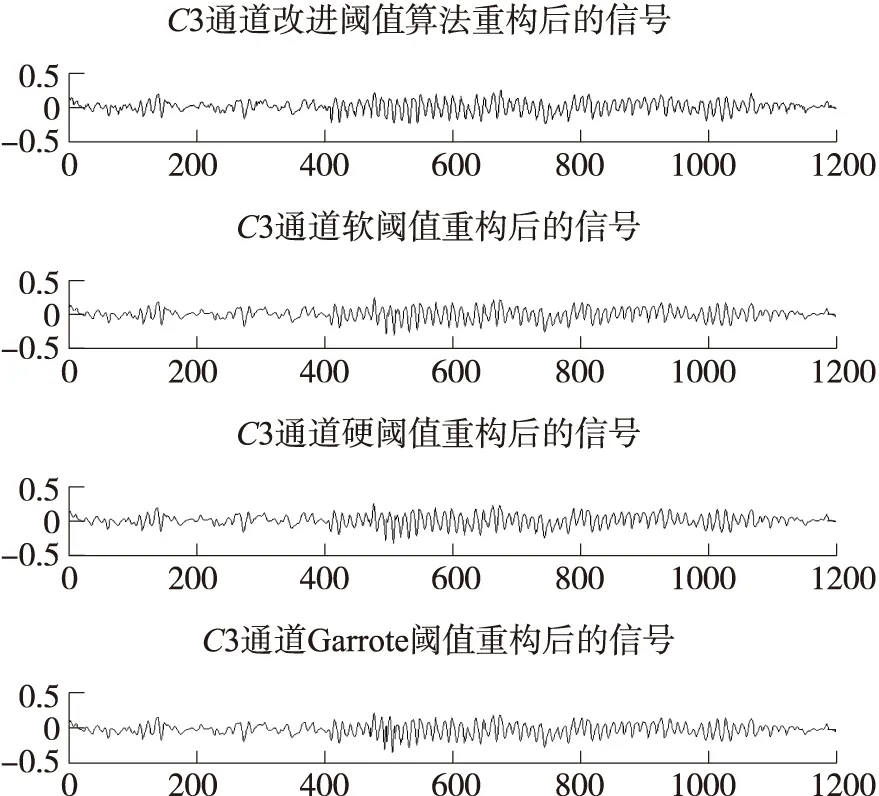
圖6 C3通道EEG去噪結果對比圖

從圖6可以看出改進閾值算法對EEG去噪效果比其他3種算法有了較大的改善,高頻部分的毛刺減少,信號更加平滑,同時與圖3原始C3通道的EEG信號變化趨勢是一致的。根據式(9)、式(10)計算出140次EEG去噪效果的SNR和RMSE,然后分別求SNR和RMSE均值和方差,得到EEG信號經過消噪后的評價指標如表3所示。圖7是使用加權閾值去噪和未使用加權閾值對C3通道的EEG信號去噪后得到的去噪圖,在表3中,以定量指標信噪比和均方根誤差作對比,可以看出加權閾值縮放因子的去噪效果更好。

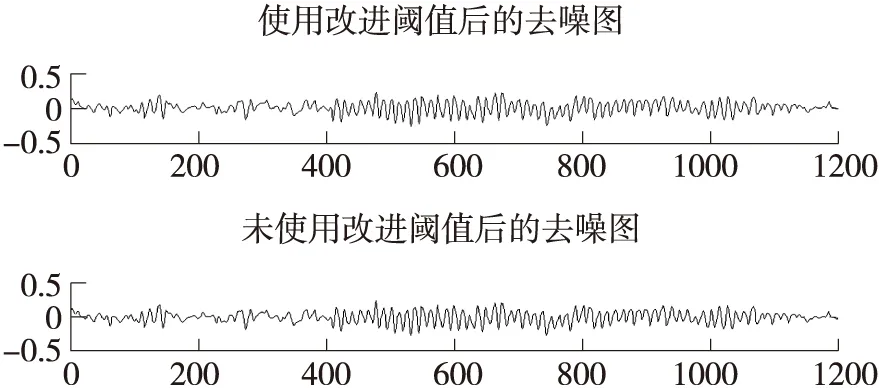
圖7 使用加權閾值縮放因子和未使用加權閾值去噪效果對比圖

表3 兩層分解時不同算法去噪效果的SNR和RMSE結果對比

從表3中對比SNR和RMSE的值,其中改進閾值算法的SNR的值最高,同時改進算法的RMSE的值最低,在定量上表明了使用改進閾值算法對EEG信號去噪的效果優于其他3種算法。由于數據是由140次測試所得,其中因測試人員注意力不集中、疲勞等原因,140次試驗中有幾組實驗數據不是很理想,如第17次、83次、117次、125次、129次采集到的數據中,信號的信噪比出現較大誤差,但不影響最終實驗結果。

5 結論

本文將小波閾值去噪法引入到腦電信號預處理中,在軟閾值算法的基礎上,提出了一種基于改進閾值算法來去除EEG信號中的噪聲信號。以去噪效果圖和SNR、RMSE作為評判去噪效果優劣的指標,不僅可以通過肉眼直接進行判斷,而且也可以從定量指標上分析去噪效果的好壞。將采集到的EEG信號分別通過改進閾值算法、硬閾值法、軟閾值法、Garrote閾值法進行去噪處理,實驗表明,改進閾值去噪算法在腦電去噪方面有很大的提高,不僅有效的抑制了高斯噪聲,同時保留EEG中大部分的有用的細節信息,為下一步的EEG特征提取和模式識別奠定良好的基礎。

[1] Zou L,Zhang Y,Yang L T,et al. Single-Trial Evoked Potentials Study by Combining Wavelet Denoising and Principal Component Analysis Methods[J]. Journal of Clinical Neurophysiology,2010,27(1):17-24.

[2]Albera L,Kachenoura A,Comon P,et al. ICA-Based EEG Denoising:a Comparative Analysis of Fifteen Methods[J]. Bulletin of the Polish Academy of Sciences:Technical Sciences,2012,60(3):407-418.

[3]萬柏坤,朱欣,楊春梅,等. ICA去除EEG中眼動偽差和工頻干擾方法研究[J]. 電子學報,2003,31(10):1571-1574.

[4]梁延研,蔡占川,李堅,等. 尺度不變V變換信號消噪[J]. 計算機學報,2013,36(9):1929-1942.

[5]董盟盟,仲鐵,徐潔,等. 基于小波分析的腦電信號處理[J]. 電子設計工程,2012,24(20):59-61.

[6]席旭剛,朱海港,羅志增. 基于EEMD和二代小波變換的表面肌電信號去噪方法[J]. 傳感技術學報,2012,25(11):1488-1493.

[7]朱曉軍,呂士欽,余雪麗,等. 基于改進EMD的腦電信號去噪方法[J]. 計算機工程,2012,1(38):151-156.

[8]王攀,沈繼忠,施錦河. 想象左右手運動的腦電特征提取[J]. 傳感技術學報,2010,23(9):1220-1225.

[9]Donoho D L,Johnston I M. Ideal Spatial Adaptive Via Wavelet Shrinkage[J]. Biometrika,1994,81:425-455.

[10]Donoho D L. De-Noising by Soft-Thresholding[J]. IEEE Trans Inf Theory,1995,41(3):613-627.

[11]Gao Hongye. Wavelet Shrinkage Denoisingm Using the Non-Negative Garrote[J]. Journal of Computational and Graphical Statistics,1998,7(4):469-488.

[12]段永剛,馬立元,李永軍,等. 基于小波分析的改進軟閾值去噪算法[J]. 科學技術與工程,2010,10(23):5755-5758.

馬玉良(1976-),男,博士,杭州電子科技大學副研究員,碩士生導師,主要從事生物信號檢測與處理、仿生假肢及其控制、智能控制等相關研究工作,mayuliang@hdu.edu.cn;

許明珍(1989-),男,碩士研究生,主要研究方向為生物信號檢測與處理、模式識別與智能控制,121060074@hdu.edu.cn;

楊家強(1970-),男,副教授,主要從事電機及其控制、機器人控制技術和機電一體化的研究,yjq1998@163.com。

De-NoisingMethodoftheEEGBasedonAdaptiveThreshold*

MAYuliang1,XUMingzhen1,SHEQingshan1,GAOYunyuan1,SUNYao1,YANGJiaqiang2*

(1.Institute of Intelligent Control and Robotics,Hangzhou Dianzi University,Hangzhou 310018,China; 2.College of Electrical Engineering,Zhejiang University,Hangzhou 310027,China)

In order to eliminate the noise mixed in Electroencephalogram(EEG)and retain useful EEG information,an EEG de-noising method based on adaptive threshold is proposed,which is improved on the basis of soft thresholding. Firstly,high frequency coefficients and low frequency coefficients of multilayer signals are obtained by wavelet decomposition. Then,detail coefficients is processed by using the adaptive threshold. Finally,the original EEG signal is resumed by reconstructing shrinked detail coefficients. The final results show that the proposed de-noising algorithm has perspective of higher SNR and lower RMSE compared to soft thresholding,hard thresholding and Garrote thresholding.

EEG signal;adaptive threshold method;SNR;RMSE

項目來源:國家自然科學基金項目(61372023,61201300,61201302,61172134);浙江省自然科學基金項目(LQ13F010014);杭州電子科技大學研究生品牌課程建設項目(PPKC2013YB006)

2014-06-06修改日期:2014-09-02

10.3969/j.issn.1004-1699.2014.10.012

TP391

:A

:1004-1699(2014)10-1368-05