移動錨節點凸規劃定位算法研究及改進

任克強,莊放望

(江西理工大學信息工程學院,江西 贛州 341000)

?

移動錨節點凸規劃定位算法研究及改進

任克強*,莊放望

(江西理工大學信息工程學院,江西 贛州 341000)

為了提高無線傳感器網絡的節點定位精度,對相關文獻進行了研究,提出了一種改進的移動錨節點凸規劃定位算法。該算法對原算法作了以下改進:利用正半定松弛方法擴大求解問題的可行域,以降低求解優化問題的計算復雜度;采用局部梯度下降法進行迭代優化來逼近最優估計,以提高優化問題的求解精度。實驗結果表明,改進算法比原算法具有更高的定位精度,并可以更好地適應不同的網絡規模。

無線傳感器網絡;定位算法;凸規劃;梯度下降法;移動錨節點

在無線傳感器網絡WSN(Wireless Sensor Network)中,對于大部分的感知任務,例如路由協議效率、定位與跟蹤、節點分簇等,獲取傳感器節點的位置信息極其重要[1]。節點定位是無線傳感器網絡的關鍵技術之一,根據定位過程中是否需要距離信息,可將定位算法分為測距相關與測距無關兩大類[2]。典型的測距相關定位算法有基于到達時間TOA(Time of arrival)定位、基于到達時間差TDOA(Time Difference of Arrival)定位、基于到達角度AOA(Angle of Arrival)定位和基于接收信號強度指示RSSI(Received Signal Strength Indicator)定位等算法[3-4],典型的測距無關定位算法有質心定位,距離向量-跳段DV-hop(Distance Vector-hop)定位,凸規劃定位、基于多維定標MDS(Multidimensional Scaling)定位等算法[5-6]。

近年來,通過優化方法來解決節點定位問題成為研究的熱點之一,許多基于規劃的定位方法逐漸被提出[7-8]。文獻[9]提出Convex定位算法,該算法將傳感器網絡中的未知節點和錨節點能否進行通信作為約束條件,通過多個鄰接錨節點的通信約束構造凸規劃問題,但通過節點通信區域交集的外接矩形面積近似通信區域交集,降低了定位精確度。文獻[10]提出了一種基于二階錐規劃松弛的分布式定位算法,盡管在凸包內的未知節點可獲得較好的定位精度,但在凸包外的未知節點定位性能較差。文獻[11]對二階錐規劃問題進行了改進,用半定松弛的方法把非凸規劃問題轉化為凸規劃問題,從而根據距離約束采用極大似然準則計算節點的位置,但定位過程中需測量未知節點與錨節點的距離。文獻[12]提出一種新的半定規劃松弛方法將最大似然估計最小二乘問題轉化為凸規劃問題,但定位過程需使用RSS測距模型。文獻[13]提出Co-SRL的凸規劃節點定位算法,以多個移動錨節點進行協作定位,并采用凸規劃方法計算節點的位置。文獻[14]提出一種高斯噪聲下基于最大分散度的半定規劃定位算法,該算法利用半定規劃,并用梯度下降法進行求精,取得了較好的定位精度。文獻[15]利用移動錨節點以不同的功率發射信標信號,將未知節點接收到的信標信息轉化為二次不等式約束組,再利用凸規劃方法計算節點的位置,取得了較高的定位精度,但定位精度還可進一步提升。因此,本文對文獻[15]的方法進行了改進,提出了一種改進的移動錨節點凸規劃定位算法,以提高節點定位的精度。

1 凸規劃定位算法

WSN中的錨節點與未知節點之間相互通信必須滿足歐幾里德距離的約束關系:

‖x-a‖≤R

(1)

其中,x為未知節點的位置,a為錨節點的位置,R為錨節點的最大傳輸半徑。

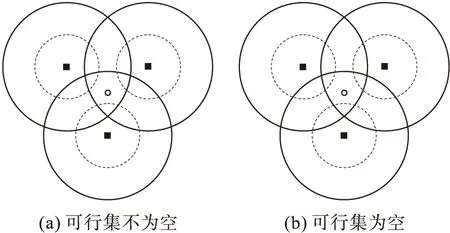
圖1 兩種定位情形

如果錨節點在不同位置以多種功率發射信標信號,則每個未知節點可獲得與自身位置x有關的不等式約束組:

rk<‖x-ak‖≤Rkk=1,2,…,n

(2)

其中,ak為k時刻錨節點的位置,rk(可能為零)和Rk為k時刻的有效約束半徑。

在多功率移動錨節點的WSN中,每個未知節點的定位問題可以轉化為二次不等式組的求解問題。但網絡環境因素的復雜性可能導致未知節點與錨節點之間不滿足通信的條件,信號的干擾、衰減等因素也會對節點定位過程造成嚴重影響。因此,可能導致兩種節點定位的情形,如圖1所示。圖1中的黑色方塊表示錨節點位置,空心圓圈表示未知節點位置;圖1(a)的可行集不為空,圖1(b)的可行集為空。

文獻[15]提出一種移動錨節點輔助的凸規劃定位算法,該算法可適用于上述兩種定位的情形,也可推廣應用于測距相關的定位系統。

根據通信約束關系,每個未知節點可以得到一組關于自身位置的約束,并通過最小化得到最優位置的逼近。

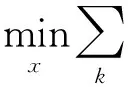
(3)

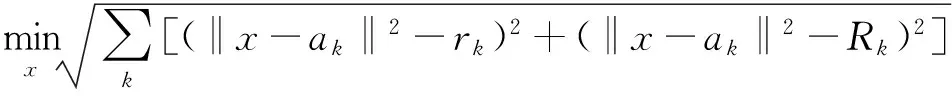
(4)

2 改進的凸規劃定位算法

文獻[15]利用凸松弛方法將式(4)的非凸規劃問題轉化為凸規劃問題,但采用這種優化方法將會增加計算復雜度,并且導致求解結果出現非最優解或可行解,這無疑降低了規劃問題求解的精度。本文對文獻[15]的方法進行了改進,利用正半定松弛方法,擴大求解問題的可行域并降低求解優化問題的計算復雜度,采用局部梯度下降法提高優化問題的求解精度。

將式(3)展開得到:

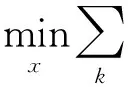
(5)

由于錨節點的有效半徑可根據其發射功率計算得到,即rk和Rk已知,故:

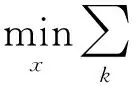
(6)

由于式(6)為非凸規劃問題,但可利用凸松弛方法將式(6)轉化為凸規劃問題。

令X=[x1,x2,…,xn]∈R2×n,Y=XTX,

μxa=‖x-ak‖2,vxa=‖x-ak‖

則式(6)中的范數部分為:

‖x-ak‖2=(ak;ei)T[I2;X]T[I2;X](ak;ei)

(7)

從而,式(6)可表示為:

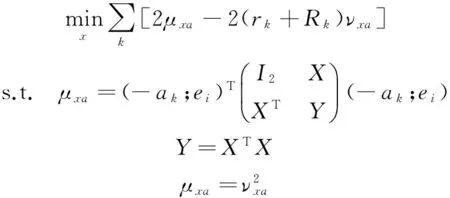
(8)

其中,I2為2維單位矩陣,ei為第i個元素為1的n維單位向量,(ak;ei)為(2+n)維列向量。

根據非凸優化理論,可以通過半定松弛方法,將非凸規劃問題轉化為凸規劃問題:

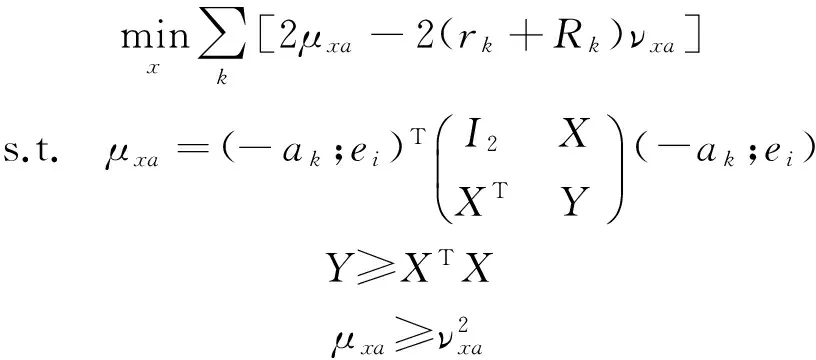
(9)

因此,可以得到式(9)凸規劃問題的一般形式:

(10)

由于半定規劃內點法產生的解具有高秩性,其松弛解可能不是最優解,甚至不是可行解。因此,通過局部梯度下降法來逼近最優解。

(11)

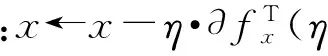
令精度為ε(ε>0),迭代次數為m(m的初值為1),則局部梯度下降法的步驟如下:

S1 以半定規劃松弛解xi(i=1,2,…,n)為初始點開始迭代;

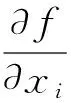
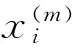
本文改進方法的計算復雜度和求解精度分析如下:

求解凸規劃問題,一般情況下,采用內點法解決n個未知節點定位問題的計算復雜度與約束條件個數有關,如果約束條件的個數在O(n)范圍內,其計算復雜度為O(n3)[16]。文獻[15]模型引入松弛后,約束條件的個數在O(n2)范圍內,故求解文獻[15]規劃問題的計算復雜度為O(n6)。而本文模型進一步松弛,式(10)中的(2+n)維矩陣錐Z可以被分解成小矩陣錐,分解后的約束條件個數在O(n)范圍內,故求解本文凸規劃問題的計算復雜度為O(n3)。因此,本文模型比文獻[15]模型運算更加快速,計算復雜度更低。

由于局部梯度下降法利用負梯度作為每次迭代的搜索方向,每次以松弛解為起點,沿著目標函數在起點處的負梯度方向改善松弛解,使之接近最優解,從而提高定位精度。因此,局部梯度下降法可以有效改善求解問題的松弛解,提高定位精度。

3 實驗結果與分析

為了驗證算法的性能,將本文算法與文獻[15]的算法進行比較實驗。實驗平臺:Windows XP SP3+MATLAB 2009a。實驗場景:2-D平面內L×L的區域隨機分布100個未知節點。實驗參數:一個移動錨節點按文獻[15]的移動路徑在網絡中移動并以兩級發射功率發送信標信號,如圖2所示,錨節點兩級發射功率對應的最大傳輸半徑分別為r和R,r=0.15L,R=2r,錨節點移動步長s=0.1L;ε=0.01,η=0.005L。

采用歸一化平均定位誤差來評估算法的性能:

(12)

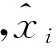
3.1 理想傳輸模型的定位

本實驗主要比較兩種方法在理想傳輸模型下的性能。

在實驗場景中隨機部署100個未知節點,分別用文獻[15]的方法和本文方法進行定位,定位結果如圖3所示,圖中星號表示實際坐標,圓圈表示估計坐標,兩者之間的連線表示定位誤差。表1為實驗場景隨機部署100次并分別用兩種方法進行定位的歸一化定位誤差。

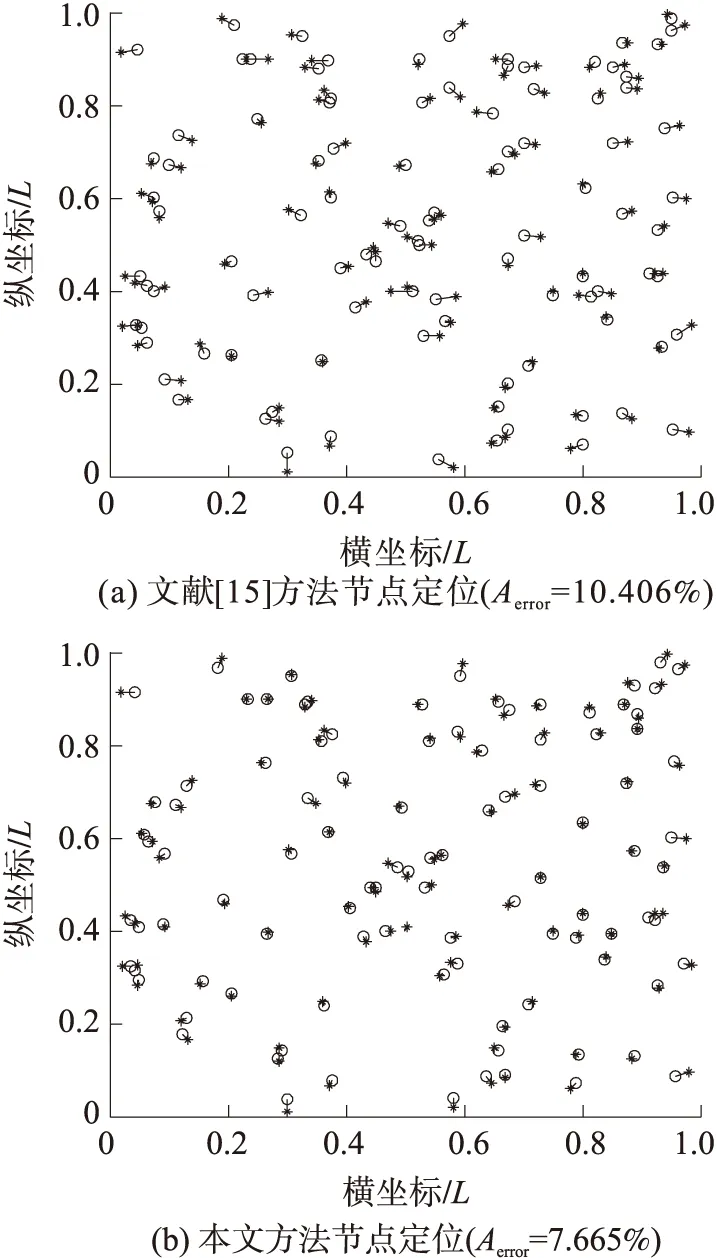
圖3 理想傳輸模型的定位結果

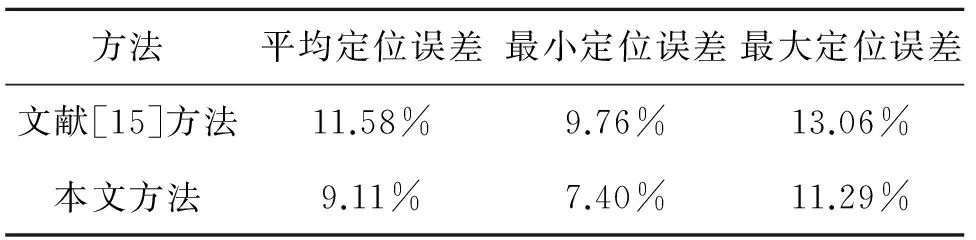
表1 理想傳輸模型的歸一化定位誤差

從圖3和表1可以看出,在理想傳輸模型下,文獻[15]取得了較高的定位精度,但由于文獻[15]只利用松弛方法對凸規劃問題進行求解,并沒有考慮松弛解的因素;而本文采用松弛方法使得凸規劃問題的可行域更大,能有效減少松弛解的數目,并且采用局部梯度下降法提高松弛解的精度,可以更有效地逼近全局最優解。因此,本文方法的定位精度比文獻[15]有了一定的提高。

3.2 非理想傳輸模型的定位

在實際環境中,由于網絡環境的復雜性及信號傳播媒介等原因,錨節點傳輸過程的通信范圍并不滿足固定的無線電射程。本實驗主要比較兩種方法在非理想傳輸模型下的性能。通過不規則信號模型來模擬實際環境,利用不規則度DOI(Degree of Irregular)來表征錨節點傳播信號在傳輸過程中受到的影響。通常,DOI為0時表示錨節點通信范圍為理想的圓形區域,DOI為0.2表示節點的有效傳輸半徑在[0.8r,1.2r]的范圍內變化,DOI越大,錨節點的通信范圍變化越大且越不規則。

在實驗場景中隨機部署100個未知節點,并在DOI=0.2時分別用文獻[15]的方法和本文方法進行定位,定位結果如圖4所示。

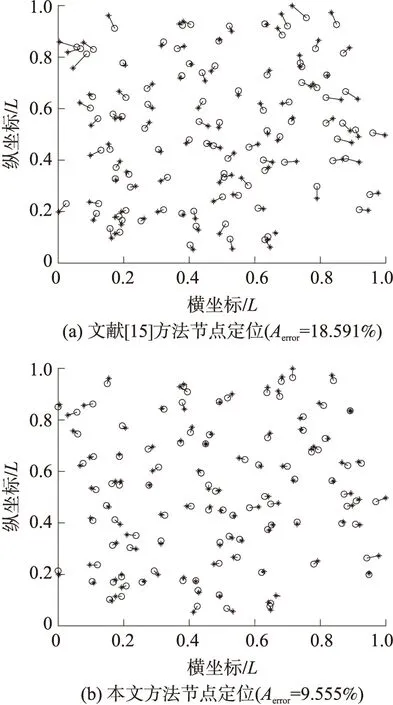
圖4 非理想傳輸模型的定位結果(DOI=0.2)

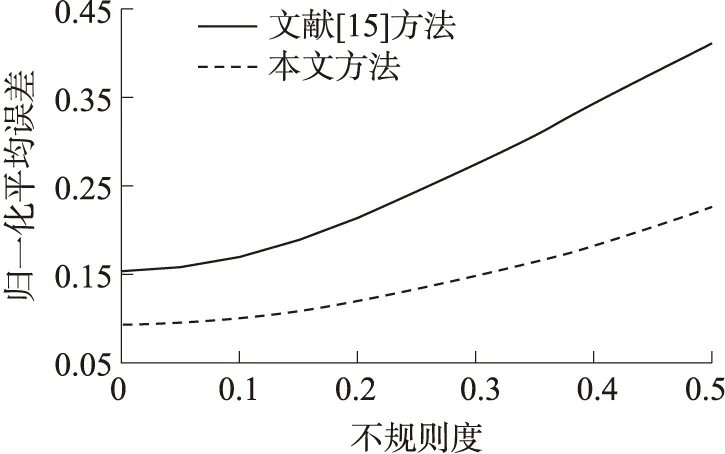
圖5 非理想傳輸模型的平均定位性能

由圖4可知,在DOI為0.2時,本文的歸一化平均誤差比文獻[15]提高了9.036%。

圖5為實驗場景隨機部署100次并在不同DOI取值時,分別用兩種方法進行定位的歸一化定位誤差。

從圖5可以看出,DOI值越小,平均定位性能越接近理想傳輸模型的平均定位性能,但是隨著DOI值的增大,定位誤差也隨之增長。由于本文方法在求解凸規劃問題的基礎上,對松弛解采用局部梯度下降法進行迭代逼近最優解,可以更好地適應實際的網絡環境,故在相同的條件下,本文的平均定位性能優于文獻[15]的定位性能。

3.3 不同錨節點傳輸半徑的定位

本實驗主要比較兩種方法在錨節點移動步長s=0.1L的條件下,錨節點最大傳輸半徑r分別取0.10L、0.15L、0.20L、0.25L、0.30L和0.35L時的性能。實驗結果如圖6所示。

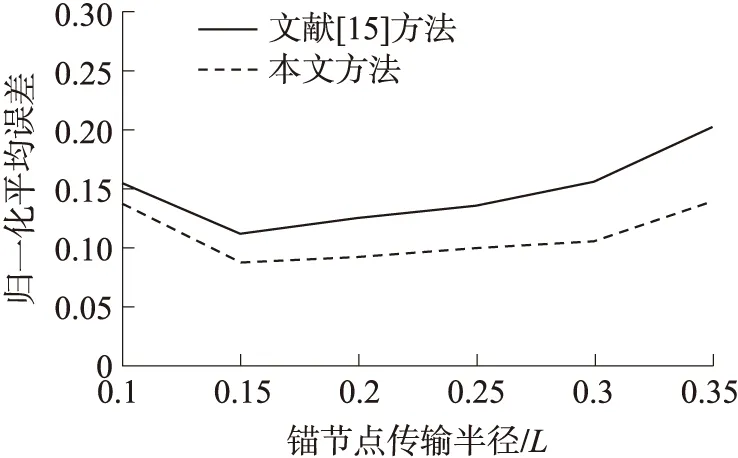
圖6 不同錨節點傳輸半徑的定位性能

從圖6可以看出,在錨節點移動步長相同、錨節點最大傳輸半徑取不同值時,本文方法通過局部梯度下降法,可有效改善松弛解,其平均定位性能優于文獻[15]的定位性能。

3.4 未知節點密度對定位性能的影響

本實驗主要比較未知節點密度對兩種方法性能的影響。在實驗場景中分別隨機部署25、50、75、100、125、150、175、200、225、250、275和300個未知節點,分別用文獻[15]的方法和本文方法進行定位,實驗結果如圖7所示。

從圖7可以看出,兩種方法在不同未知節點密度的定位性能均較平穩,但本文方法在不同未知節點密度下的定位性能均優于文獻[15],因此,本文方法可以更好地適應于不同的網絡規模。

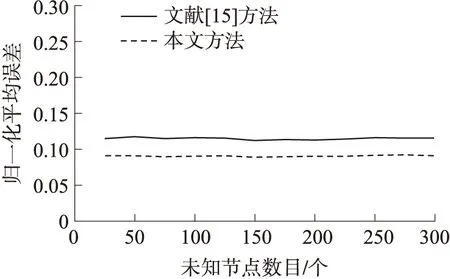
圖7 不同未知節點密度的定位性能

4 結束語

針對移動錨節點凸規劃定位算法的不足,提出了一種改進的移動錨節點凸規劃定位算法。改進算法從求解優化問題的計算復雜度和求解精度兩個方面對原算法作了改進,并在理想傳輸模型、非理想傳輸模型、不同錨節點傳輸半徑以及未知節點密度的實驗場景中進行了算法性能比較實驗。實驗結果表明,改進算法的定位精度和網絡適應性均優于原算法,從而驗證了改進措施的有效性。

[1] Akyildiz I F,Su W,Sankarasubramaniam Y,et al. Wireless Sensor Networks:A Survey[J]. Computer Networks,2002,38(4):393-422.

[2]王福豹,史龍,任豐原. 無線傳感器網絡中的自身定位系統和算法[J]. 軟件學報,2005,16(5):857-868.

[3]Park J W,Park D H,Lee C. Angle and Ranging Based Localization Method for Ad Hoc Network[J]. The Journal of Supercomputing,2013,64(2):507-521.

[4]梅舉,陳滌,辛玲. 基于蒙特卡洛方法的移動傳感網節點定位優化算法[J]. 傳感技術學報,2013,26(5):689-694.

[5]Ma D,Er M J,Wang B,et al. Range-Free Wireless Sensor Networks Localization Based on Hop-Count Quantization[J]. Telecommunication Systems,2012,50(3):199-213.

[6]黃亮,王福豹,段渭軍,等. 基于距離重構的無線傳感器網絡多維定標定位算法[J]. 傳感技術學報,2013,26(9):1284-1287.

[7]Chiu W Y,Chen B S,Yang C Y. Robust Relative Location Estimation in Wireless Sensor Networks with Inexact Position Problems[J]. IEEE Transactions on Mobile Computing,2012,11(6):935-946.

[8]Ji S,Sze K F,Zhou Z,et al. Beyond Convex Relaxation:a Polynomial-Time Non-Convex Optimization Approach to Network Localization[C]//Proceedings of IEEE International Conference on Computer Communications(INFOCOM),Turin,Italy:IEEE,2013:2499-2507.

[9]Doherty L,El Ghaoui L. Convex Position Estimation in Wireless Sensor Networks[C]//Proceedings of IEEE International Conference on Computer Communications(INFOCOM). Anchorage USA:IEEE. 2001,3:1655-1663.

[10]Srirangarajan S,Tewfik A H,Luo Z Q. Distributed Sensor Network Localization Using SOCP Relaxation[J]. IEEE Transactions on Wireless Communications,2008,7(12):4886-4895.

[11]Xie S,Wang J,Hu A,et al. Localization Algorithm Based on Positive Semi-Definite Programming in Wireless Sensor Networks[J]. International Journal of Signal Processing,Image Processing and Pattern Recognition,2013,6(1):1-12.

[12]Vaghefi R M,Gholami M R,Buehrer R M,et al. Cooperative Received Signal Strength-Based Sensor Localization with Unknown Transmit Powers[J]. IEEE Transactions on Signal Processing 2013,61(6):1389-1403.

[13]Liu W,Sun D,Ren P,et al. Co-SRL:A Convex Optimization Algorithm for Anchor Localization in Wireless Sensor Networks[C]//Proceedings of 2013 AASRI Conference on Parallel and Distributed Computing and Systems,Singapore,2013,5:62-66.

[14]何國鋼,鄧平. 一種高斯噪聲下基于最大分散度的WSN半定規劃定位算法[J]. 傳感技術學報,2012,25(8):1116-1120.

[15]史清江,何晨. 多功率移動錨節點輔助的分布式節點定位方法[J]. 通信學報,2009,30(10):8-13.

[16]Biswas P,Ye Y. Semidefinite Programming for Ad Hoc Wireless Sensor Network Localization[C]//Proceedings of the 3rd International Symposium on Information Processing in Sensor Networks. ACM,2004:46-54.

任克強(1959-),男,教授,碩士研究生導師,主要研究方向為嵌入式系統、無線傳感器網絡等,jxrenkeqiang@163.com;

莊放望(1988-),男,碩士研究生,主要研究方向為無線傳感器網絡。

ResearchandImprovementofMobileAnchorNodeLocalizationAlgorithmBasedonConvexProgramming

RENKeqiang*,ZHUANGFangwang

(School of Information Engineering,Jiangxi University of Science and Technology,Ganzhou Jiangxi 341000,China)

In order to enhance the node localization accuracy in wireless sensor networks,this article had studied the related references,and proposed an improved convex programming localization algorithm of mobile anchor node. The algorithm made some improvements on the original algorithm to reduce the computational complexity of solving optimization problems,positive semidefinite relaxation method was utilized for enlarging the feasible region of solving problems to improve the accuracy of solving optimization problems and local gradient descent method was used to approximate the optimal estimate. The experimental results show that the algorithm has higher positioning accuracy than the original algorithm,and can better adapt to the different network scale.

wireless sensor network;localization algorithm;convex optimization;gradient descent method;mobile anchor node

2014-06-28修改日期:2014-08-26

10.3969/j.issn.1004-1699.2014.10.019

TP393

:A

:1004-1699(2014)10-1406-06