含隨機參數的空間柔性梁動力學模型
靳紅玲,陳建軍,趙 寬,曹鴻鈞
(西安電子科技大學 電子裝備結構設計教育部重點實驗室,西安 710071)
隨含柔性構件的機械裝置向高速、輕質、高精度方向發展,柔性體大范圍剛體運動與彈性變形耦合作用不可忽視。Kane等[1]認為懸臂梁作高速旋轉時橫向振動較穩定,與零次近似模型發散結論相反,并首次提出動力剛化概念。文獻[2-7]對動力剛化進行研究,提出以計入橫向彎曲引起縱向縮短的二階耦合變形量為主要方法的剛柔耦合動力學建模法。此動力學方程在結構上均較零次耦合模型增加由二階耦合變形量引入關于廣義坐標的一階或高階量,若保留一階量忽略更高階量,模型即為一次近似耦合模型。理論分析及實驗已證明一次近似耦合模型在小變形下的合理性及正確性。
傳統柔體動力學研究中認為研究對象所有物理參數均為確定的、或可精確測量的;但實際中因設計公差、制造誤差及環境溫度等多種隨機因素的存在,使基于確定性參數的動力學建模及分析結果不能真實描述實際柔體的動力學行為。因此,研究不確定性參數柔體動力學問題具有重要理論與實際工程意義。關于不確定性參數的柔體動力學研究鮮有報道。文獻[8]對計及參數不確定性柔性空間曲線梁的動力學建模進行研究,并利用蒙特卡洛模擬法(Monte Carlo simulation, MCS)求解;但該法需樣本量大、效率較低。多項式混沌(Polynomial Chaos,PC)方法用于具有不確定性參數的流體力學、結構力學及車輛動力學等分析中[9-11],該方法與MCS法相比,在保證計算精度前提下可減少模擬次數、提高計算效率。
本文在一次近似耦合模型[4]基礎上利用多項式混沌結合高效回歸法,對含隨機參數空間柔性梁的動力響應求解問題進行研究,并以空間自旋柔性梁為對象,分析其各參數隨機性對動力響應影響。
1 多項式混沌
考慮在概率空間充分光滑模型
Y=u(x)
(1)
式中:u(x)為通常不能顯式表示、但可通過數值模擬等方法輸出的響應量。
為求解Y的統計特性,較有效方法為尋找代理模型以減少計算時間。PC即為理想模型[12]:
(2)
式中:n為隨機變量個數;y=[y0,y1,…,yn,y11,…,ynn,…]為待定系數矢量;ξ=(ξ1,…,ξn)為服從標準正態分布的隨機變量矢量,Γd(ξi1,…,ξid)為d階Hermite多項式:
Γd(ξi1,…,ξid)=
(3)
數值計算只能取有限項近似表示輸出響應量。精度達p階的PC可簡化為
(4)
式中:N為多項式混沌展開式所含待定系數個數:
(5)
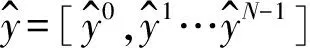
〈Hi,Hj〉=∫Rnω(ξ)Hi(ξ)Hj(ξ)dξ?δij
(6)
式中:δij為Kronecker張量;ω(ξ)為權函數,表達式為
(7)
研究顯示[13],混沌展開的階數越高,作為替代模型的PC將越接近原模型,但求解系數所需方程個數會隨之快速增加,計算成本顯著增加。通常取2階PC即可獲得對Y較理想近似,當2階PC不能滿足精度要求時才考慮更高階的混沌展開。
英、漢語言富具文化意象。這些意象有時通用,有時卻只是英、漢語言各自獨有。如何翻譯這些富含語言、文化特色的意象,譯者翻譯的主觀能動性至關重要。是盡量保留這些意象,還是轉換意象,或者干脆舍棄意象,翻譯的目的決定原文信息在譯文中要不要體現,或者以何種方式體現。試看一例:

2 隨機參數柔性梁動力學模型建立
柔性體動力學分析中出現多種描述動力學方程形式。本文采用空間柔性梁彈性動力學微分方程[4]為
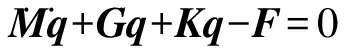
(8)
式中:M,C,K,F分別為質量矩陣、陀螺矩陣、剛度矩陣及力矩陣,表達式分別為
(9)
(10)
(12)
式中:各參數具體含義見文獻[4]。
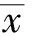
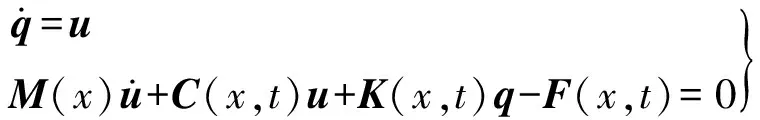
(13)
按式(4)分別對輸入隨機變量xj、輸出隨機變量qi、ui進行多項式混沌展開:
(14)
(15)
(16)
式中:s為隨機解維數。
將式(14)~式(16)代入式(13),得
(17)
(18)
式中:H=(H0,…,HN-1);Q為關于M,C,K,F的函數關系式。
用Galerkin法對式(18)映射得
(19)
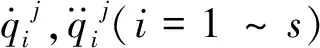
(20)
t時刻待定系數可通過線性回歸法獲得
(21)
(22)
yt確定后即可據此系數求解響應隨機變量的數字特征。
q均值即為隨機多項式展開的0次項[7]:
(23)
q方差表達式為
(24)
歸納以上求解過程,給出求解隨機參數空間柔性梁動力響應的流程見圖1,m為時間節點總數。

圖1 柔性梁變形響應數字特征的求解流程圖

圖2 自旋空間梁
3 算 例
圖2為作大范圍運動的自旋空間柔性梁,長L=10 m,橫截面為矩形,一端固結在旋轉的剛性圓柱上,并隨圓柱一同作定軸旋轉,忽略梁的軸向變形。圖2中O0-x0y0z0為慣性坐標系,Ob-xbybzb為浮動坐標系。將梁橫截面高度y、寬度z、彈性模量E及體密度ρ均視為相互獨立且服從正態分布的隨機參數,其均值分別為μy=μ1=0.10 m,μz=μ2=0.07 m,μE=μ3=7×1010N/m2,μρ=μ4=3×103kg/m3。為便于比較各隨機參數取值分散性對梁動力響應影響,取所有隨機參數的變異系數γall相等,且γall=γy=γz=γE=γρ=0.05。
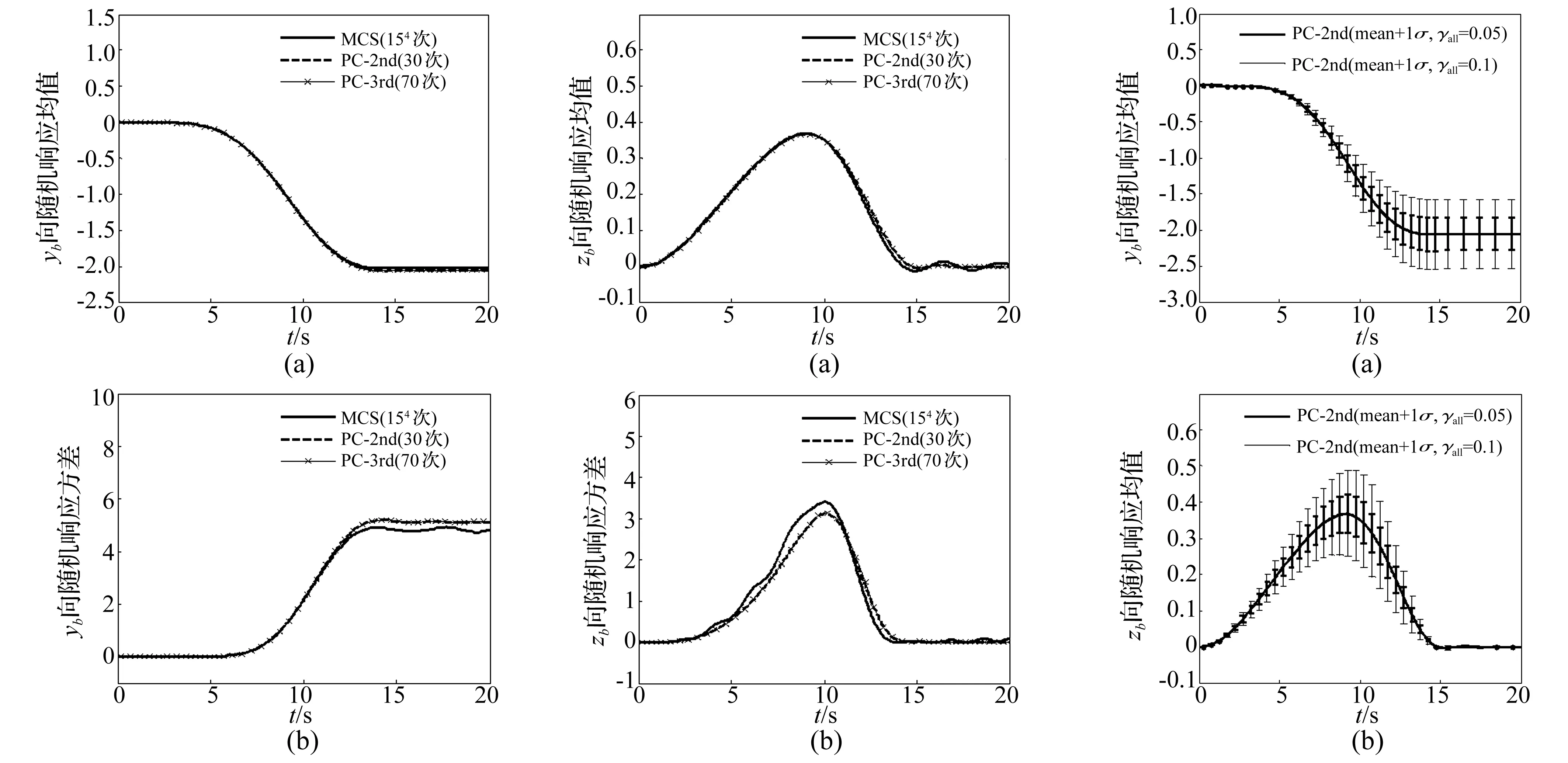
圖3 梁端點yb方向隨機響應均值及方差
給定梁軸線與角速度夾角α=45°為常數,梁端直接固結于Y0軸,即R=0,剛性圓柱角速度規律為
式中:Ts為達到恒定轉速前加速時間,取Ts=15 s;Ωs為t>Ts時恒定轉速,取Ωs=3 rad/s。
本文分別采用二、三階多項式混沌結合高效回歸法求解該空間柔性梁變形響應。據上述求解步驟,通過Matlab分別模擬30、70次,獲得響應均值及方差,并與模擬154次MCS所得結果進行對比。利用PC與MCS方法所得柔性梁自由端b點變形響應量yb,zb的均值、方差隨時間變化曲線見圖3、圖4。

表1 不同隨機變量對柔性梁變形響應數字特征影響

圖6 不同隨機參數的隨機響應方差
為考察各隨機參數分散性對彈性梁自由端b點變形響應影響,給出隨機參數變異系數分別為γall=0.05,γall=0.1時四隨機參數組合的隨機模型響應均值及由一倍均方差σ所得誤差棒見5圖,PC方法在變異系數γall,γy,γz,γE,γρ分別為0.05時隨機模型響應方差見圖6,前20 s內不同隨機參數組合的隨機模型自由端b點變形響應(均值、方差)絕對值最大值見表1。
由圖3~圖6及表1看出,本文二、三階多項式混沌法模擬自由端位移響應均值、方差結果高度一致,表明二階方法可收斂;本文方法與MCS方法所得響應均值、方差結果較接近說明本文方法的正確性及有效性;所有隨機參數變異系數越小,響應均方差越小,但響應均值基本保持不變;物理參數E的分散性對yb及zb兩方向響應的分散性影響較大,而ρ的分散性對yb、zb兩方向響應的分散性影響可忽略,幾何參數y的分散性僅對彈性梁yb方向響應分散性影響較大,參數z的分散性僅對zb方向響應分散性影響較大。
4 結 論
本文首次將基于高效回歸法多項式混沌用于含隨機參數空間柔性梁動力學問題分析中獲得較好效果,結論如下:
(1) 基于隨機響應面法的多項式混沌可用于含多個隨機參數的柔性體動力響應分析,與MCS法相比,在隨機參數較多時只需較少次數分析即可獲得響應的主要數字特征,計算效率明顯提高。
(2) 各參數隨機性對柔性體動力響應影響不可忽略,欲增強柔性體動力響應的平穩性,應先降低對柔性體動力響應影響較大參數的分散性。
(3) 通過MCS驗證表明,本文所建含隨機參數的空間柔性梁動力學模型合理,且能客觀反映實際工程中剛柔耦合體動力學行為。
[1] Kane T R, Ryan R R, Banerjee A K.Dynamics of a cantilever beam attached to a moving base[J].Journal of Guidance Control Dynamics, 1987, 10(2):139-150.
[2] Yoo H H, Chung J.Dynamics of rectangular plates undergoing prescribed overall motion[J].Journal of Sound Vibration,2001, 239(1):123-137.
[3] 楊輝, 洪嘉振, 余征躍.動力剛化問題的實驗研究[J].力學學報, 2004, 36 (1): 118-124.
YANG Hui, HONG Jia-zhen, YU Zheng-yue.Experimental investigation on dynamic stiffening phenomenon[J].Acta Mechanica Sinica, 2004, 36 (1): 118-124.
[4] Liu J Y, Hong J Z.Dynamics of three-dimensional beams undergoing large overall motion[J].European Journal of Mechanics A/Solids, 2004, 23(6):1051-1068.
[5] 和興鎖,鄧峰巖,王睿.具有大范圍運動和非線性變形的空間柔性梁的精確動力學建模[J].物理學報, 2010, 59(3): 1428-1435.
HE Xing-suo, DENG Feng-yan, WANG Rui.Exact dynamic modeling of a spatial flexible beam with large overall motion and nonlinear deformation[J].Acta Physica Sinica, 2010, 59 (3):1428-1435.
[6] 吳勝寶,章定國.大范圍運動剛體-柔性梁剛柔耦合動力學分析[J].振動工程學報, 2011, 24 (1): 1-7.
WU Sheng-bao, ZHANG Ding-guo.Rigid-flexible coupling dynamic analysis of hub-flexible beam with large overall motion[J].Journal of Vibration Engineering,2011,24(1): 1-7.
[7] 方建士,章定國.旋轉懸臂梁的剛柔耦合動力學建模與頻率分析[J].計算力學學報, 2012, 29 (3): 333-339.
FANG Jian-shi, ZHANG Ding-guo.Rigid-flexible coupling dynamic modeling and frequency analysis of a rotating cantilever beam[J].Chinese Journal of Computational Mechanics, 2012, 29 (3): 333-339.
[8] 張海根,何柏巖,王樹新,等.計及參數不確定性的柔性空間曲線梁動力學建模方法[J].天津大學學報, 2003,36(1): 37-40.
ZHANG Hai-gen, HE Bai-yan, WANG Shu-xin, et al.Dynamic model of flexible spatial camber beam with uncertainty parameters[J].Journal of Tianjin University, 2003,36(1):37-40.
[9] Spanos P, Ghanem R.Boundary element method analysis for random vibration problems[J].Journal of Engineering Mechanics, 1991, 117(2): 409-423.
[10] Sandu A, Sandu C, Ahmadian M, et al.Modeling multibody systems with uncertainties.part I: theoretical and computational aspects[J].Multibody System Dynamics, 2006, 15:369-391.
[11] Sandu C, Sandu A, Ahmadian M, et al.Modeling multibody systems with uncertainties.part II: numerical applications[J].Multibody System Dynamics, 2006, 15: 241-262.
[12] Ghanem R, Spanos P.Stochastic finite elements: a spectral approach[M].New York: Mineola, Dover publications Inc, 1991.
[13] Isukapalli S S, Roy A, Georgopoulos P.Stochastic response surface methods (SRSM) for uncertainty propagation: application to environmental and biological systems[J].Risk Analysis, 1998, 18(3):351-363.
[14] Tatang M A, Pan W, Prinn R G., et al.An efficient method for parametric uncertainty analysis of numerical geophysical models[J].Journal of Geophysical Research, 1997, 102(D18): 21925-21932.
[15] Isukapalli S S.Uncertainty analysis of transport-transformation models[D].New Brunswick: New Jersey, 1999.

