基于6σ的車身噪聲傳遞函數(shù)穩(wěn)健優(yōu)化設(shè)計(jì)

聶祚興, 于德介, 周建文, 周 舟

(1.中國汽車工程研究院股份有限公司，重慶 4000392.湖南大學(xué) 汽車車身先進(jìn)設(shè)計(jì)制造國家重點(diǎn)實(shí)驗(yàn)室，長沙 410082)

車身噪聲傳遞函數(shù)(Noise Transfer Function，NTF)反映車身結(jié)構(gòu)與內(nèi)部空腔間聲學(xué)特性，對(duì)駕駛室噪聲控制有重要影響。車身噪聲傳遞函數(shù)能在車身設(shè)計(jì)階段通過聲固耦合分析準(zhǔn)確預(yù)估，盡早發(fā)現(xiàn)、修正潛在的設(shè)計(jì)問題，可為車內(nèi)噪聲預(yù)估控制提供依據(jù)。由于對(duì)駕駛舒適性要求的不斷提高，車身噪聲傳遞函數(shù)指標(biāo)頗受設(shè)計(jì)者重視。

工程實(shí)際中，設(shè)計(jì)參數(shù)特性具有統(tǒng)計(jì)分散性，傳統(tǒng)確定性優(yōu)化往往會(huì)因參數(shù)不確定性導(dǎo)致原精確結(jié)果不可行甚至設(shè)計(jì)失敗。在汽車產(chǎn)品設(shè)計(jì)過程中，只有充分考慮參數(shù)的統(tǒng)計(jì)分散性，進(jìn)行基于不確定性優(yōu)化設(shè)計(jì)，才能降低產(chǎn)品對(duì)生產(chǎn)制造及使用過程對(duì)不確定性參數(shù)靈敏度，提高實(shí)際工作過程中使用性能。可靠性優(yōu)化設(shè)計(jì)考慮各設(shè)計(jì)參數(shù)不確定性，將確定的約束條件變?yōu)楦怕始s束條件，使最優(yōu)解向可行域方向移動(dòng)，使產(chǎn)品可靠性要求得到滿足[1]，而穩(wěn)健優(yōu)化設(shè)計(jì)[2-3]不僅在滿足可靠性要求條件下使結(jié)構(gòu)性能達(dá)到最優(yōu)，且能降低約束條件目標(biāo)變量對(duì)設(shè)計(jì)變量變化的靈敏度，即提高系統(tǒng)穩(wěn)健性。6σ穩(wěn)健優(yōu)化設(shè)計(jì)將6σ質(zhì)量管理、可靠性優(yōu)化設(shè)計(jì)與穩(wěn)健設(shè)計(jì)相結(jié)合，在使“目標(biāo)函數(shù)均方差最小”基礎(chǔ)上考慮包括設(shè)計(jì)變量、約束條件目標(biāo)函數(shù)所有不確定性信息，要求產(chǎn)品質(zhì)量在均值6σ范圍內(nèi)波動(dòng)時(shí)均能滿足，使產(chǎn)品可靠度達(dá)到99.999 999 8%。由于6σ穩(wěn)健優(yōu)化設(shè)計(jì)能使不確定性因素對(duì)產(chǎn)品的作用效果達(dá)到最小化，目前已廣泛用于設(shè)計(jì)、開發(fā)及生產(chǎn)制造等領(lǐng)域。文獻(xiàn)[4]將6σ穩(wěn)健優(yōu)化設(shè)計(jì)用于薄板沖壓成型中，用其自主開發(fā)的STLMesher軟件建立模具參數(shù)化模型，將試驗(yàn)設(shè)計(jì)、近似模型蒙與特卡羅模擬技術(shù)結(jié)合，構(gòu)造基于產(chǎn)品質(zhì)量工程的6σ穩(wěn)健優(yōu)化設(shè)計(jì)方法，并取得良好效果。文獻(xiàn)[5]結(jié)合多目標(biāo)遺傳算法與6σ實(shí)驗(yàn)設(shè)計(jì)，提出基于6σ的多目標(biāo)穩(wěn)健優(yōu)化設(shè)計(jì)方法，分別以理論測(cè)試函數(shù)及實(shí)際焊接梁為例，驗(yàn)證該方法的有效性。文獻(xiàn)[6]為消除設(shè)計(jì)參數(shù)波動(dòng)及使用環(huán)境對(duì)高溫超導(dǎo)電纜影響,提高設(shè)計(jì)效率，提出基于6σ穩(wěn)健優(yōu)化設(shè)計(jì)的HTS電纜優(yōu)化方法，使優(yōu)化結(jié)果不僅達(dá)到電流均勻分配，且顯著提高產(chǎn)品的可靠性與穩(wěn)健性。

為保證汽車NVH性能，設(shè)計(jì)中對(duì)車身噪聲傳遞函數(shù)進(jìn)行優(yōu)化。由于眾多車身板件在生產(chǎn)制造及使用環(huán)境中存在各種不確定性，會(huì)致可行的設(shè)計(jì)不可靠甚至失敗。對(duì)此，本文將6σ穩(wěn)健優(yōu)化設(shè)計(jì)方法引入車身噪聲傳遞函數(shù)設(shè)計(jì)。為減少計(jì)算量，在汽車聲固耦合有限元模型基礎(chǔ)上采用基于試驗(yàn)設(shè)計(jì)的二階多項(xiàng)式響應(yīng)面模型，以車身總質(zhì)量一階模態(tài)頻率為約束條件,駕駛員耳旁聲壓級(jí)響應(yīng)均方根值為目標(biāo)函數(shù)，在基本隨機(jī)變量概率特性已知情況下對(duì)車身噪聲傳遞函數(shù)進(jìn)行6σ穩(wěn)健優(yōu)化設(shè)計(jì)。結(jié)果表明6σ穩(wěn)健優(yōu)化設(shè)計(jì)方法獲得優(yōu)化解的同時(shí)，能較大幅度提高優(yōu)化設(shè)計(jì)結(jié)果的穩(wěn)健性。

1 車身噪聲傳遞函數(shù)

車身噪聲傳遞函數(shù)指施加于車身特定位置單位力在車內(nèi)產(chǎn)生的內(nèi)部聲壓,表示車身結(jié)構(gòu)與內(nèi)部空腔間的聲學(xué)特性，對(duì)動(dòng)力總成與路面激勵(lì)引起的駕駛室噪聲有重要影響[7]。將車身結(jié)構(gòu)視為彈性體,車室空腔聲壓變化會(huì)激勵(lì)車身壁板產(chǎn)生振動(dòng), 而車身壁板振動(dòng)又會(huì)通過對(duì)臨近空氣壓迫改變車室內(nèi)聲壓[8]。考慮耦合效應(yīng)情況，車內(nèi)聲腔有限元方程表示為

(1)

式中:[Mf]為聲腔聲學(xué)質(zhì)量矩陣；[Kf]為聲腔聲學(xué)剛度矩陣；{p}為各節(jié)點(diǎn)聲壓向量；[S]為結(jié)構(gòu)聲學(xué)耦合矩陣；ρ為空氣密度；c為聲波在媒介中傳播速度。

受空氣作用影響的車身結(jié)構(gòu)有限元方程為

(2)

式中:[Ms]為車身結(jié)構(gòu)質(zhì)量矩陣；[Ks]為車身結(jié)構(gòu)剛度矩陣；{u}為各節(jié)點(diǎn)位移向量；{Fs}為結(jié)構(gòu)廣義外力向量；{pa}為邊界節(jié)點(diǎn)聲壓向量。

合并整理式(1)、(2)，得聲固耦合系統(tǒng)有限元方程為

(3)

簡諧激勵(lì)下聲固耦合振動(dòng)及聲壓響應(yīng)值為

u=[(Ks-Msω2)-[S](Kf-Mfω2)-1ω2(ρ[S]T)]-1Fs

(4)

p=(Kf-Mfω2)-1ω2(ρ[S]T)u

(5)

用一定頻率步長范圍、單位簡諧激振力施加于車身特定位置時(shí)，由式(5)可得系統(tǒng)對(duì)寬頻激勵(lì)的響應(yīng)值，即激勵(lì)點(diǎn)到參考位置車身噪聲傳遞函數(shù)。

2 響應(yīng)面模型構(gòu)建

響應(yīng)面法將實(shí)驗(yàn)設(shè)計(jì)與理論統(tǒng)計(jì)相結(jié)合[9]，能通過簡單多項(xiàng)式逼近復(fù)雜的隱式函數(shù)。因此能克服在噪聲傳遞函數(shù)分析及優(yōu)化中因計(jì)算成本所致瓶頸問題。

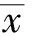
(6)

用實(shí)驗(yàn)設(shè)計(jì)方法在設(shè)計(jì)空間選適當(dāng)樣本點(diǎn)，將所得系統(tǒng)響應(yīng)與設(shè)計(jì)變量最小二乘原理擬合得近似模型，其確定的函數(shù)關(guān)系可表示為

(7)

常用二階多項(xiàng)式響應(yīng)面模型可表示為

(8)

同理，可定義三階、四階或更高階多項(xiàng)式響應(yīng)面模型。

響應(yīng)面法通過適當(dāng)少樣本的實(shí)驗(yàn)設(shè)計(jì)，即可建立設(shè)計(jì)變量與聲壓響應(yīng)的映射關(guān)系。工程中，在滿足精度情況下用響應(yīng)面近似模型進(jìn)行數(shù)值優(yōu)化，可有效避免對(duì)結(jié)構(gòu)及聲學(xué)矩陣的梯度運(yùn)算，減少聲固耦合矩陣運(yùn)算次數(shù)，提高優(yōu)化效率[10]。

3 基于6σ的車身噪聲傳遞函數(shù)穩(wěn)健優(yōu)化設(shè)計(jì)

6σ穩(wěn)健優(yōu)化設(shè)計(jì)與傳統(tǒng)確定性優(yōu)化設(shè)計(jì)相比不僅優(yōu)化設(shè)計(jì)目標(biāo)，且能降低約束條件目標(biāo)變量對(duì)設(shè)計(jì)變量變化的靈敏度，即提高系統(tǒng)穩(wěn)健性。

傳統(tǒng)確定性優(yōu)化模型為

(9)

基于優(yōu)化模型得確定性最優(yōu)點(diǎn)A見圖1。由圖1看出,考慮參數(shù)在±Δx范圍內(nèi)變化時(shí)，A點(diǎn)處響應(yīng)波動(dòng)ΔFA超出約束邊界，設(shè)計(jì)失敗。點(diǎn)B為在滿足可靠度要求前提下設(shè)計(jì)響應(yīng)可靠性最優(yōu)值,雖在±Δx范圍內(nèi)響應(yīng)波動(dòng)ΔFB未超出約束邊界，但與C點(diǎn)相比其對(duì)設(shè)計(jì)變量x敏感性高穩(wěn)健性差。穩(wěn)健性最優(yōu)解點(diǎn)C不僅在滿足約束前提下具有較好的設(shè)計(jì)響應(yīng)值，且考慮參數(shù)在±Δx范圍內(nèi)變化時(shí)，其響應(yīng)波動(dòng)僅為ΔFC，穩(wěn)健性更好。因此，穩(wěn)健優(yōu)化設(shè)計(jì)應(yīng)綜合考慮設(shè)計(jì)變量、約束條件不確定性目標(biāo)函數(shù)的期望特性[11]。

圖1 確定性優(yōu)化與不確定優(yōu)化對(duì)比

在式(9)基礎(chǔ)上，考慮參數(shù)的波動(dòng)變化，6σ穩(wěn)健優(yōu)化模型[12]

(10)

式中:n為σ水平數(shù)，本文取n=6;μx,σx為設(shè)計(jì)變量均值、標(biāo)準(zhǔn)差;μy,σy為函數(shù)響應(yīng)均值、標(biāo)準(zhǔn)差，為保證設(shè)計(jì)穩(wěn)健性足夠，應(yīng)有μy-nσy≥質(zhì)量標(biāo)準(zhǔn)下限值,μy+nσy≤質(zhì)量標(biāo)準(zhǔn)上限值。

為最小化響應(yīng)波動(dòng)性能，目標(biāo)函數(shù)表示為

(11)

式中:w1i,w2i為加權(quán)系數(shù);s1i,s2i為目標(biāo)均值及波動(dòng)比例因子;Mi為響應(yīng)目標(biāo)值;L為性能響應(yīng)數(shù)量。

圖2 車身噪聲傳遞函數(shù)6σ穩(wěn)健優(yōu)化設(shè)計(jì)流程

綜合式(10)、(11)知，6σ穩(wěn)健優(yōu)化數(shù)學(xué)模型中包含設(shè)計(jì)變量、約束條件、目標(biāo)函數(shù)均值、標(biāo)準(zhǔn)差及相關(guān)不確定信息，能使優(yōu)化設(shè)計(jì)目標(biāo)達(dá)到期望值，并使響應(yīng)波動(dòng)最小化，提高系統(tǒng)穩(wěn)健性。對(duì)車身噪聲傳遞函數(shù)進(jìn)行6σ穩(wěn)健優(yōu)化設(shè)計(jì)時(shí)，為減少計(jì)算工作量、提高優(yōu)化效率，在車身聲耦合有限元模型基礎(chǔ)上建立目標(biāo)及約束函數(shù)響應(yīng)面模型，對(duì)選定參數(shù)給定參數(shù)概率特性進(jìn)行6σ穩(wěn)健優(yōu)化設(shè)計(jì),見圖2。

4 實(shí)例

4.1 車身聲固耦合有限元模型與噪聲傳遞函數(shù)

本文以某型轎車[13]為例進(jìn)行車身噪聲傳遞函數(shù)的6σ穩(wěn)健優(yōu)化設(shè)計(jì)。獲得必要精度后對(duì)車身適當(dāng)簡化，忽略車身結(jié)構(gòu)零件中小孔、凸臺(tái)、倒角及附加件等。車身結(jié)構(gòu)有限元模型與聲腔有限元模型見圖3、圖4，其中車身結(jié)構(gòu)有限元模型主要以四邊形殼單元為主，單元總數(shù)22 472，節(jié)點(diǎn)總數(shù)20 303；聲腔模型外表面由車身結(jié)構(gòu)確定，單元類型為六面體。空氣密度1.21 kg/mm3，聲速343 m/s。

圖3 車身結(jié)構(gòu)有限元模型

在汽車NVH性能分析中需計(jì)算前副車架與車身連接的4個(gè)安裝點(diǎn)、后副車架與車身連接的4個(gè)安裝點(diǎn)及前懸架彈簧左右安裝點(diǎn)至車內(nèi)參考點(diǎn)的噪聲傳遞函數(shù)。本文以前懸架彈簧左側(cè)安裝點(diǎn)為例進(jìn)行穩(wěn)健優(yōu)化設(shè)計(jì)。將車身結(jié)構(gòu)模型聲腔模型耦合，在車身懸架左側(cè)彈簧處施加單位垂向簡諧激勵(lì),并選定駕駛員右耳處為車內(nèi)噪聲參考點(diǎn)。分析頻率范圍20～180 Hz，步長2 Hz，用Nastran軟件中模態(tài)頻率響應(yīng)算法求解，獲得車身噪聲傳遞函數(shù)。

4.2 基于實(shí)驗(yàn)設(shè)計(jì)的響應(yīng)面模型

考慮汽車整體參數(shù)確定后尺寸變化的困難性及計(jì)算復(fù)雜程度，為簡化計(jì)算，本例主要以各板件厚度為優(yōu)化設(shè)計(jì)參數(shù)，以板件材料(鋼)屬性為“噪聲”因素，且各參數(shù)均正態(tài)分布，具體是表1。

表1 參數(shù)及概率分布表

對(duì)所選參數(shù)在定義域內(nèi)進(jìn)行拉丁超立方采樣，采樣次數(shù)120，計(jì)算各采樣點(diǎn)聲壓響應(yīng)，利用最小二乘法建立駕駛員耳旁聲壓響應(yīng)均方根值的二階多項(xiàng)式響應(yīng)面模型為

P=59.838+2.611t1+1.031t2+1.044t3-1.901t4+

0.105t1t2-1.121t1t3-0.107t1t4-1.189t1t5+

0.327t1t6-0.965t2t3-0.426t2t4-0.033t2t5+

0.521t2t6+0.863t3t4-0.327t3t5+0.064t3t6-

0.086t4t5-0.127t4t6+0.197t5t6

(12)

為保證整車一階扭轉(zhuǎn)模態(tài)與發(fā)動(dòng)機(jī)剛體轉(zhuǎn)動(dòng)模態(tài)及橫向模態(tài)分離，使一階扭轉(zhuǎn)頻率遠(yuǎn)離發(fā)動(dòng)機(jī)怠速運(yùn)行時(shí)的爆發(fā)頻率，以車身結(jié)構(gòu)一階扭轉(zhuǎn)模態(tài)頻率值為約束條件，保證優(yōu)化后頻率值不低于32 Hz。建立一階扭轉(zhuǎn)固有頻率的二階多項(xiàng)式響應(yīng)面模型為

ω=30.867+4.777t1-2.412t2-0.374t3-0.180t4+

0.935t1t2-0.940t1t3-0.036t1t4+0.682t1t5+

0.461t1t6-0.265t2t3-0.126t2t4+0.756t2t5+

0.237t2t6+0.136t3t4-0.212t3t5+0.239t3t6-

0.373t4t5-0.126t4t6-0.272t5t6

(13)

圖5 聲壓響應(yīng)均方根值響應(yīng)面模型試驗(yàn)點(diǎn)相對(duì)誤差曲線

由復(fù)相關(guān)系數(shù)分析相對(duì)誤差曲線知，所得響應(yīng)面模型精度較高，擬合結(jié)果可靠，可用于優(yōu)化設(shè)計(jì)。

原車身總質(zhì)量363.75kg，考慮汽車輕量化要求，將其作為另一約束條件，對(duì)優(yōu)化后車身質(zhì)量限制在 364kg內(nèi)。據(jù)車身結(jié)構(gòu)有限元模型，車身總質(zhì)量為

m=306.576+19.804t1+8.943t2+3.964t3+

4.883t4+14.415t5+15.599t6

(14)

4.3 6σ穩(wěn)健優(yōu)化設(shè)計(jì)及結(jié)果分析

在車身懸架左側(cè)彈簧處施加單位垂向諧波激勵(lì)，以駕駛員右耳位置為車內(nèi)噪聲參考點(diǎn)計(jì)算車身噪聲傳遞函數(shù)，分析頻率范圍為20～180 Hz。以參考點(diǎn)聲壓級(jí)峰值為目標(biāo)函數(shù)，以一階扭轉(zhuǎn)固有頻率及車身總質(zhì)量為約束條件對(duì)車身噪聲傳遞函數(shù)進(jìn)行6σ穩(wěn)健優(yōu)化設(shè)計(jì)。車身噪聲傳遞函數(shù)穩(wěn)健優(yōu)化的數(shù)學(xué)模型可表示為

(15)

式中:tiu,til分別為設(shè)計(jì)變量上、下限(表1)。

分別用確定性優(yōu)化算法及6σ穩(wěn)健優(yōu)化算法對(duì)目標(biāo)函數(shù)進(jìn)行優(yōu)化，考慮實(shí)際車身板件厚度加工要求，將優(yōu)化計(jì)算所得結(jié)果保留兩位小數(shù)后圓整，并分別計(jì)算可靠度及σ水平，結(jié)果見表2、表3。

表2 確定性優(yōu)化設(shè)計(jì)結(jié)果

表3 6σ穩(wěn)健優(yōu)化優(yōu)化設(shè)計(jì)結(jié)果

由表2、表3知，頂棚、后輪罩內(nèi)板、后側(cè)圍、前地板、儀表板均較接近約束邊界，可靠度低，車身質(zhì)量可靠度僅78.9%。設(shè)計(jì)變量變化時(shí)，極易造成因約束失效設(shè)計(jì)失敗。確定性優(yōu)化設(shè)計(jì)結(jié)果目標(biāo)函數(shù)均值為58.227 dB，標(biāo)準(zhǔn)差0.293，6σ穩(wěn)健設(shè)計(jì)目標(biāo)函數(shù)均值為59.148 dB，略高于確定性優(yōu)化結(jié)果，但不僅降低目標(biāo)函數(shù)隨設(shè)計(jì)變量波動(dòng)大小，使標(biāo)準(zhǔn)差降為0.022，且所有設(shè)計(jì)變量及約束條件均遠(yuǎn)離約束邊界，達(dá)到6σ水平，可靠度達(dá)100%。

將基于響應(yīng)面的優(yōu)化結(jié)果代入聲固耦合有限元模型，獲得優(yōu)化前后駕駛員耳旁噪聲響應(yīng)曲線見圖7。與響應(yīng)面法預(yù)測(cè)結(jié)果相比，精確模型確定性優(yōu)化聲壓均方根值為58.407 dB，相對(duì)誤差為0.31%；6σ穩(wěn)健優(yōu)化聲壓均方根值為59.072 dB，相對(duì)誤差為0.13%。6σ穩(wěn)健優(yōu)化設(shè)計(jì)使駕駛員耳旁聲壓均方根值降低1.223 dB，分析頻段內(nèi)聲壓峰值由75.987 dB降至74.408 dB，降低1.579 dB，表明優(yōu)化方案可行。

5 結(jié) 論

本文在設(shè)計(jì)變量概率特性已知條件下，基于響應(yīng)面模型對(duì)某型汽車車身噪聲傳遞函數(shù)進(jìn)行6σ穩(wěn)健優(yōu)化設(shè)計(jì)，結(jié)論如下：

(1) 響應(yīng)面模型能在保證計(jì)算精度前提下快速準(zhǔn)確獲得汽車車身噪聲傳遞函數(shù)的優(yōu)化結(jié)果，大幅減少計(jì)算工作量，提高優(yōu)化效率。

(2) 與確定性優(yōu)化相比，6σ穩(wěn)健優(yōu)化設(shè)計(jì)不僅能優(yōu)化車身噪聲傳遞函數(shù)，使設(shè)計(jì)目標(biāo)達(dá)到期望水平，亦能提高優(yōu)化設(shè)計(jì)結(jié)果的穩(wěn)健性，使聲壓響應(yīng)方差最小化，具有重要應(yīng)用價(jià)值。

[1] Youn B D, Choi K K.Enriched performance measure approach for reliability-based design optimization[J].AIAA, 2005,43(4): 874-884．

[2] Li Y Q, Cui Z S, Ruan X Y, et al.CAE-based six sigma robust optimization for deep-drawing sheet metal process [J].The International Journal of Advanced Manufacturing Technology,2006,30(7/8):631-637.

[3] Feldner M,Waukesha D.A six sigma approach to improving exhaust valve reliability in a stoichiometric natural gas engine[C].Internal Combustion Engine Division 2009 Spring Technical Conference.Milwaukee: ASME,2009．

[4] 孫光永,李光耀,陳濤,等.基于6 的穩(wěn)健優(yōu)化設(shè)計(jì)在薄板沖壓成形中的應(yīng)用[J].機(jī)械工程學(xué)報(bào), 2008,44(11):248-254.

SUN Guang-yong, LI Guang-yao, CHEN Tao, et al.Sheet metal forming based six sigma robust optimization design [J].Chinese Journal of Mechanical Engineering, 2008,44(11): 248-254.

[5] Shimoyama K, Oyama A, Fujii K.A new efficient and useful robust optimization approach design for multi-objective six sigma[J].Evolutionary Computation, Edinburgh: IEEE,2005,1:950-957.

[6] Liu Xin-ying, Wang Shu-hong, Qiu Jie, et al.Robust optimization in HTS cable based on design for six sigma [J].IEEE Transactions on Magnetics,2008,44(6):978-981.

[7] 黃金陵.汽車車身設(shè)計(jì)[M].北京:機(jī)械工業(yè)出版社,2007.

[8] 凱莫爾,沃爾夫.現(xiàn)代汽車結(jié)構(gòu)[M].北京:人民交通出版社, 1987.

[9] Wang C H, Hsu Y.Enhancing rubber component reliability by response model[J].Computers & Industrial Engineering, 2009, 57(3):806-812．

[10] 臧獻(xiàn)國,于德介,姚凌云.響應(yīng)表面法在結(jié)構(gòu)噪聲優(yōu)化中的應(yīng)用研究[J].噪聲與振動(dòng)控制,2009,24(4):116-119.

ZANG Xian-guo,YU De-jie,YAO Ling-yun.Application Study of response surface method in structure-born noise optimization[J].Noise and Vibration Control,2009,24(4): 116-119.

[11] Sun Guang-yong, Li Guang-yao, Gong Zhi-hui, et al.Multiobjective robust optimization method for drawbead design in sheet metal forming[J].Materials and Design,2010,31(4):1917-1929．

[12] Koch P N, Yang R J, Gu L.Design for six sigma through robust optimization[J].Struct Multidisc Optim, 2004, 26(3/4): 235-248．

[13] 李增剛,詹福良.Virtual.Lab Acoustic聲學(xué)仿真計(jì)算高級(jí)應(yīng)用實(shí)例[M].北京: 國防工業(yè)出版社,2010.