一種七自由度冗余機械臂的奇異構形特征分析

， ，

(哈爾濱工業(yè)大學機器人技術與系統(tǒng)國家重點實驗室，黑龍江 哈爾濱 150001)

一種七自由度冗余機械臂的奇異構形特征分析

史士財，尹斌，蔣再男

(哈爾濱工業(yè)大學機器人技術與系統(tǒng)國家重點實驗室，黑龍江 哈爾濱 150001)

總結了對七自由度冗余機械臂進行奇異性分析的常用方法，并引入了一種基于相關旋量抑制的方法。采用這種方法，對一種構型與加拿大臂2相同的七自由度冗余機械臂進行了奇異性分析，得出了七自由度冗余機械臂出現(xiàn)奇異時的5種情況。為了深入和形象地理解機械臂的奇異構形，針對每種情況進行了詳細分析，得出了每種情況對應的奇異構形的幾何特征，并用圖解形式直觀地給出了奇異構形的例子。

七自由度冗余機械臂；奇異性分析；相關旋量抑制方法；奇異構形特征

0 引言

七自由度機械臂是能夠完成多維空間任務的冗余機械臂中結構最為簡單的，同時也具有了操作靈活、避障、避奇異和力矩優(yōu)化等優(yōu)點，因而得到學術界的關注，并得到廣泛應用。加拿大臂2(Canadarm2)[1]和SPDM(special purpose dexterous manipulator)[2]都采用了七自由度的構形，并在國際空間站的建設和維護中做出重要貢獻。七自由度冗余機械臂的奇異性分析，為機器人機構設計和控制器算法設計提供了理論基礎[3-7]。在此，采用了參考文獻[5]中提出的相關旋量抑制的方法，分析了一種七自由度冗余機械臂的奇異性。

1 相關旋量抑制的方法

相關旋量抑制的方法是一種針對七自由度冗余機械臂失去1個自由度的奇異性分析方法，這種方法簡化了奇異性分析的復雜運算過程。對一個七自由度冗余機械臂，它的旋量矩陣可以表示為[$]=[$1$2$3$4$5$6$7]，$i為第i關節(jié)的旋量。當機械臂處于奇異構形時，這個6×7的旋量矩陣將欠秩。為了方便敘述，稱這7個關節(jié)旋量中任意6個的集合為基旋量，對應的旋量矩陣稱為基子矩陣。采用該方法，對七自由度機械臂進行奇異性分析，需要經(jīng)過以下2步。

a.找出基子矩陣不滿秩的條件。當基子矩陣不滿秩時，滿足以下等式：

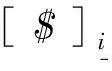
(1)

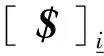
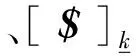
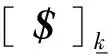
(2)

聯(lián)立式(1)、式(2)，可以得到七自由度冗余機械臂出現(xiàn)奇異構形的條件。

2 一種七自由度機械臂的奇異性分析

2.1 七自由度機械臂的運動學模型

本次的研究對象是一個七自由度機械臂，采用R⊥R⊥R∥R∥R⊥R⊥R的自由度配置，R代表旋轉關節(jié)，⊥代表2個關節(jié)的軸線相互垂直，∥代表2個關節(jié)的軸線相互平行，與Canadarm2構型[8]相同，但結構參數(shù)不一樣。該機械臂的D-H參數(shù)如表1所示。

表1 七自由度機械臂D-H參數(shù)

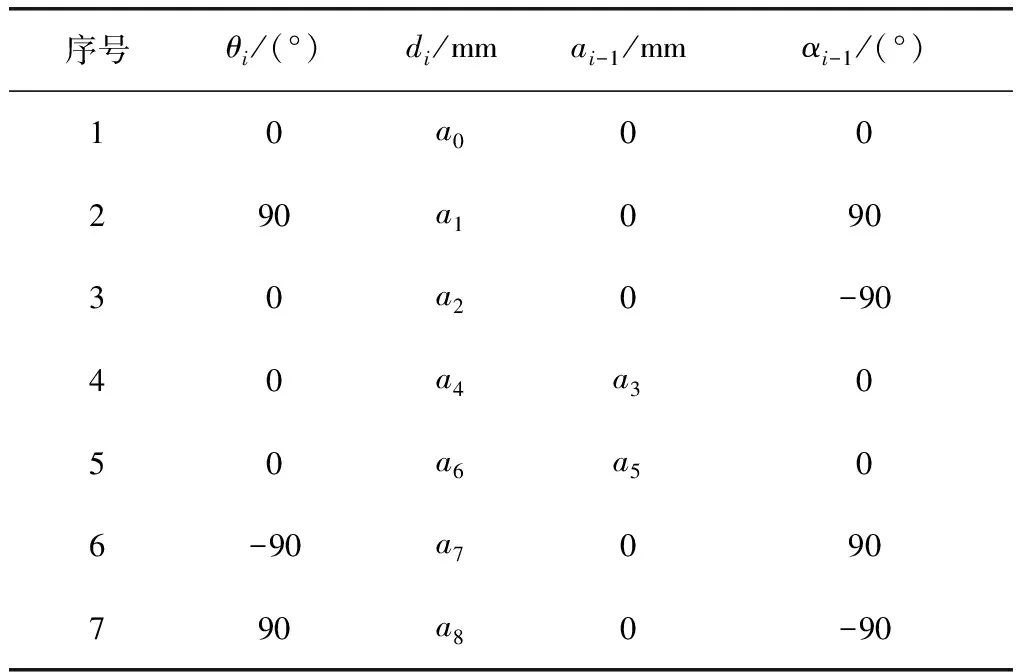
序號θi/(°)di/mmai-1/mmαi-1/(°)10a000290a109030a20-9040a4a3050a6a506-90a7090790a80-90

由于關節(jié)1的旋量表達式較為復雜，故選擇關節(jié)2～關節(jié)7的關節(jié)旋量作為基旋量。同時，為簡化關節(jié)旋量的計算[9]，選擇關節(jié)5的坐標系F5-x5y5z5為參考坐標系計算各個關節(jié)的旋量。該七自由度冗余機械臂的關節(jié)旋量矩陣為：

5[$]=[5$15$25$35$45$55$65$7]

基子矩陣為：

(3)

2.2 基子矩陣欠秩的條件

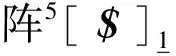
s4s6(a3c3+a3c34+a6s345)=0

(4)

要使式(4)成立，需滿足以下情況。

第1種情況：

s4=0

(5)

第2種情況：

s6=0

(6)

第3種情況：

a3c3+a3c34+a6s345=0

(7)

2.3 旋量矩陣欠秩的額外條件

基子矩陣不滿秩的條件有3種情況，如式(5)～式(7)。在此，將針對每種情況，先找出相關旋量，然后計算抑制矩陣不滿秩的條件，從而得出旋量矩陣欠秩的額外條件。

2.3.1 第1種情況

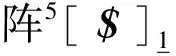
(8)

2.3.2 第2種情況

推導方法與第1種情況相同，在此不再贅述，直接給出結果。這種情況下七自由度冗余機械臂出現(xiàn)奇異分別有2種情況：

(9)

(10)

2.3.3 第3種情況

推導方法與第1種情況相同，在此不再贅述，直接給出結果。這種情況下七自由度冗余機械臂出現(xiàn)奇異分別有2種情況：

(11)

(12)

機械臂的關節(jié)角度關系只要在滿足5個方程式組中的任意1個，就會出現(xiàn)失去1個自由度的奇異構形。

3 七自由度機械臂奇異構形的特征分析及圖解

為了對七自由度機械臂的奇異構形有一個形象的理解，分析了機械臂出現(xiàn)奇異時所具有的構形特征，對每種情況給出例子，用圖解的形式來表示。

3.1 第1種情況

這種情況對應式(8)。s4=0，即關節(jié)4的角度為0°或±180°，又關節(jié)3，4，5的軸線相互平行，故關節(jié)3，4，5的軸線共面。

第2個式子由于過于復雜，沒有分析出它對應的幾何意義。但此時可以看作是關節(jié)4固定，即等價為一個構型為R⊥R⊥R∥R⊥R⊥R的六自由度機械臂，失去1個自由度時的奇異構形。這里給出這種情況下的特例，各個關節(jié)的角度為[0° 0° 0° 0° 0° 0° 0°]，即機械臂處于零位姿時，機械臂的構形如圖1所示；各個關節(jié)角度為[0° 0° 0° 180° 0° 0° 0°]時，機械臂的構形如圖2所示。

語文組“深入”探討此次研學活動后，對以下四方面進行了整合思考：（1）跨學科主題與學科內(nèi)主題的整合（天壇的傳統(tǒng)文化）；（2）研究課程的“縱深”關系（研究話題的整合，任務直指核心能力）；（3）研學活動的傳統(tǒng)文化價值；（4）“后研學”活動的開展。

圖1 第1種奇異構形的例子1

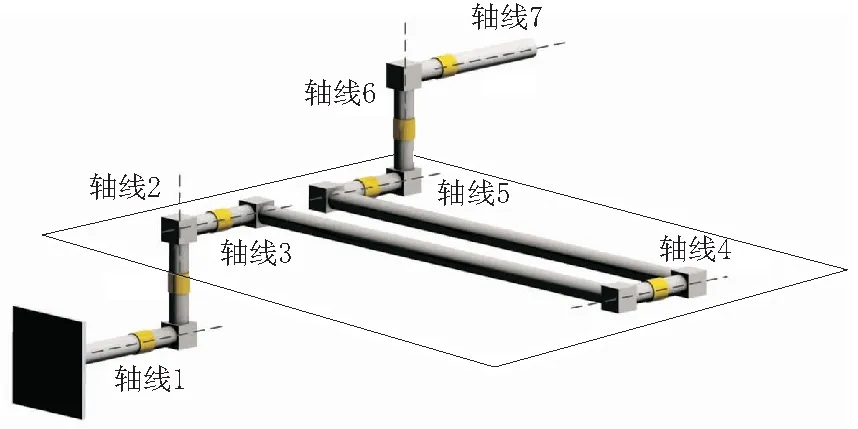
圖2 第1種奇異構形的例子2

3.2 第2種情況

這種情況對應式(9)。此時，關節(jié)2角度為0°或±180°，意味著關節(jié)1的軸線與關節(jié)3的軸線平行；關節(jié)6角度為0°或±180°，意味著關節(jié)7的軸線與關節(jié)5的軸線平行。又因為關節(jié)3，4，5的軸線相互平行，因此，這種情況下機械臂的奇異構形特征是：關節(jié)1，3，4，5，7的軸線相互平行。

這里給出這種情況下的例子，取各個關節(jié)的角度為[0° 0° 20° 50° -30° 180° 70°]，機械臂的構形如圖3所示。

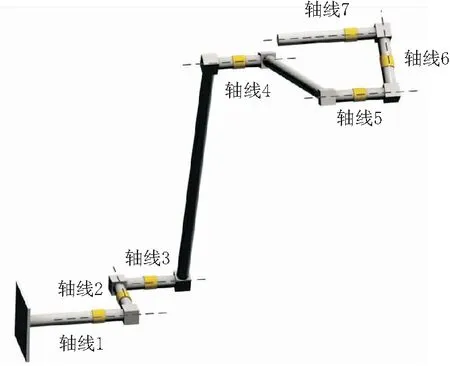
圖3 第2種奇異構形的例子

3.3 第3種情況

這種情況對應式(10)。

a.分析1。關節(jié)6角度為0°或±180°，則關節(jié)7的軸線與關節(jié)5的軸線平行，6號坐標系的y-z平面與關節(jié)7的軸線、關節(jié)5的軸線形成的平面共面。

b.分析2。1號坐標系到6號坐標系的齊次變換矩陣的(1，4)元素，即x分量為c6(-a3c5-a3c45+a1s345)，顯然，此時x分量為0，即1號坐標系的原點位于6號坐標系的y-z平面上。

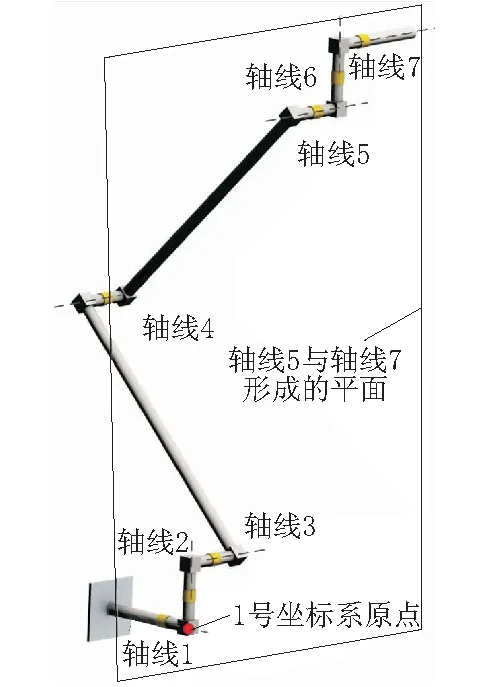
圖4 第3種奇異構形的特例

綜上可知，這種情況下機械臂的奇異構形特征為：關節(jié)7的軸線與關節(jié)5的軸線平行，且1號坐標系原點位于關節(jié)7的軸線、關節(jié)5的軸線所形成的y-z平面上。

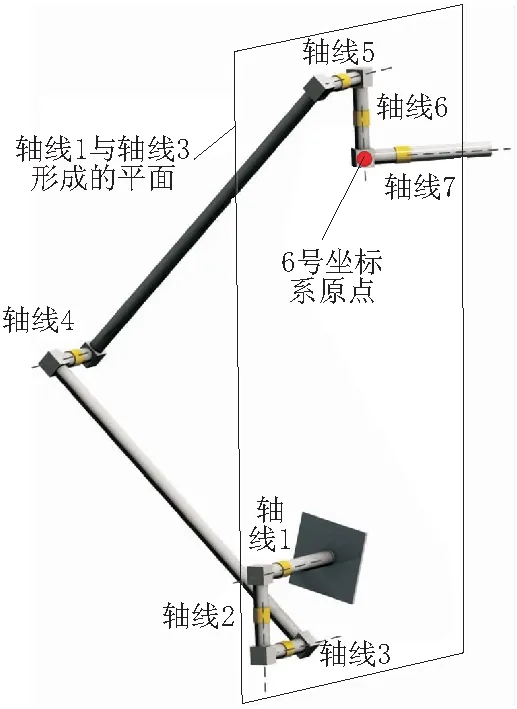
圖5 第4種奇異構形的例子

3.4 第4種情況

這種情況對應式(11)。

a.分析1。s2=0，則關節(jié)1的軸線與關節(jié)3的軸線平行，2號坐標系的y-z平面與關節(jié)1的軸線和關節(jié)3軸線形成的平面共面。

b.分析2。6號坐標系到2號坐標系的齊次變換矩陣的(1，4)元素，即x分量為a3c3+a3c34+a6s345，顯然，x分量為0，即6號坐標系的原點位于2號坐標系的y-z平面。

綜上可知，這種情況下機械臂的奇異構形特征是：關節(jié)1的軸線平行于關節(jié)3的軸線，且6號坐標系原點位于關節(jié)1的軸線和關節(jié)3的軸線所形成的平面上。

這里給出這種情況下的一個特例，各個關節(jié)的角度為[15° 180° 45° 90° -135° 45° 30°]，機械臂的構形如圖5所示。

3.5 第5種情況

這種情況對應式(12)。

a.分析1。6號坐標系到2號坐標系的齊次變換矩陣的(1，4)元素，即x分量為a3c3+a3c34+a6s345，顯然，x分量為0，即6號坐標系的原點位于2號坐標系的y-z平面。

b.分析2。6號坐標系到1號坐標系的齊次坐標變換矩陣的(2，4)元素，即y分量為-a1+a3s3+a3s34-a6c345，顯然，y分量為0，即6號坐標系的原點位于1號坐標系的x-z平面。

綜上可知，這種情況下的奇異構形特征是：6號坐標系的原點位于一條線上，這條線是由1號坐標系的x-z平面和2號坐標系的y-z平面相交形成的。

這里給出這種情況下的一個特例，各個關節(jié)的角度為[0° 0° 80.319° 175° -99.681° 45° 0°]，機械臂的構形如圖6所示。

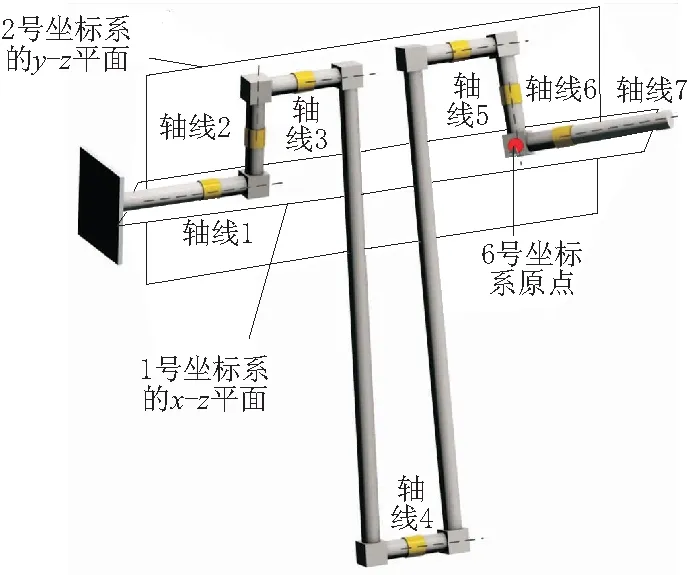
圖6 第5種奇異構形的例子

4 結束語

采用相關旋量抑制的方法，對一種構型與Canadarm2相同的七自由度機械臂進行了奇異性分析，得出了機械臂出現(xiàn)奇異的5種條件。為使對七自由度冗余機械臂奇異構形的理解不局限在公式層面，詳細分析了每種條件，給出了每種條件對應的奇異構形特征，并用圖解形式直觀地給出了奇異構形的例子。所用的分析方法和結論,適用于與本文機械臂構型相同的任何七自由度冗余機械臂。

[1] 張凱鋒，周 暉，溫慶平，等.空間站機械臂研究[J].空間科學學報，2010，30(6)：612-619.

[2] Coleshill E，Oshinowo L，Rembala R，et al. Dextre: improving maintenance operations on the international space station[J]. Acta Astronautica，2009，64(9):869-874.

[3] 丑武勝，吳 忠，王田苗，等.冗余機械臂運動奇異性分析[J].機械工程學報，2000，36(9)：33-36.

[4] Nokleby S B. Singularity analysis of the Canadarm2[J]. Mechanism and Machine Theory，2007，42(4):442-454.

[5] Kong X，Gosselin C M. A dependent-screw suppression approach to the singularity analysis of a 7-DOF redundant manipulator:Canadarm2[J]. Transactions of the Canadian Society for Mechanical Engineering，2005，29(4):593-604.

[6] Boudreau R，Podhorodeski R P. Singularity analysis of a kinematically simple class of 7-jointed revolute manipulators[J]. Transactions of the Canadian Society for Mechanical Engineering，2010，34(1):105-117.

[7] Xu W F，Zhang J T，Qian H H，et al. Identifying the singularity conditions of canadarm2based on elementary Jacobian transformation[C]// IEEE/RSJ International Conference on Intelligent Robots and Systems，Tokyo，Japan，2013:795-800.

[8] Gibbs G，Sachdev S. Canada and the international space station program: overview and status[J].Acta Astronautica，2002，51(1):591-600.

[9] Waldron K J，Wang S L，Bolin S J.A study of the Jacobian matrix of serial manipulators[J].Journal of Mechanisms，Transmissions and Automation in Design，1985，107(2):230-238.

Features Analysis of Singular Configurations of a 7-DOF Redundant Manipulator

SHIShicai，YINBin，JIANGZainan

(State Key Laboratory of Robotics and System，Harbin Institute of Technology，Harbin 150001，China)

Popular methods for singular analysis of a 7degrees of freedom (DOF) redundant manipulator are summarized. A depend-screw suppression approach is introduced and applied to the singular analysis of a 7-DOF redundant manipulator，whose configuration is identical with Canadarm2. Five sets of conditions defining singular configurations are obtained. In order to have a deep and visual understanding of singular configurations，each condition is analyzed in detail. Geometric features and illustration of singular configurations of the 7-DOF manipulator are presented.

7-DOF redundant manipulator; singularity analysis; dependent-screw suppression approach; feature of singular configurations

2014-06-05

國家自然科學基金資助項目(51305097)；教育部博士點基金資助項目(20122302120046)

TP24

A

1001-2257(2014)10-0067-04

史士財(1978-)，男，遼寧遼中人，博士，副研究員，研究方向為機器人技術；尹斌(1989-)，男，河南新鄭人，碩士，研究方向為機器人技術；蔣再男(1982-)，男，安徽岳西人，博士，助理研究員，研究方向為空間機器人遙操作、人機交互技術。