旋翼槳葉結構載荷計算方法比較研究

吳 杰, 楊衛東, 虞志浩

(南京航空航天大學 直升機旋翼動力學重點實驗室，南京 210016)

直升機旋翼動力學的挑戰之一是精確地預測槳葉結構振動載荷。除了結構動力學建模與氣動力建模精度對載荷有重要影響外，載荷計算方法也同樣是非常重要的因素。Bielawa[1]最早采用力積分法與模態疊加法兩種載荷計算方法對無鉸式旋翼開始了這方面的研究。文章指出力積分法雖然能得到更準確的結果，并且能以更少的模態收斂，但其實現過程更為復雜。Thomas[2]利用CAMRAD對幾種直升機旋翼槳葉(BO105，CH-34及SA349/2)進行了力積分法與曲率法的對比研究。他指出當剖面之間的槳葉結構特性相差不大時，曲率法能獲得較好的載荷；而力積分法則依賴積分步長以及槳葉分段數的選擇，并且彎矩預測比剪力預測需要更多的分段數和更小的積分步長。上世紀八十年代，反力法在著名的旋翼動力學綜合分析平臺2GCHAS中被引入。Lim等[3]利用2GCHAS以及CAMRAD/JA研究了UH-60A直升機結構載荷數據。文章認為曲率法的缺點在于高階導數引起的數值精度損失；同時力積分法很難處理近槳根處的載荷計算，因為槳根處剖面特性變化通常較為劇烈；而反力法采用了有限元方程中組集之前的單元矩陣計算節點載荷，預測精度較高。

本文著重比較上述三種載荷計算方法對于槳葉結構載荷的影響。采用剛柔耦合模型[4]描述旋翼槳葉的動力學運動關系。該模型將鉸接式旋翼鉸與軸承處的轉角抽象成三個獨立自由度，作為剛體轉角與槳葉彈性變形耦合，相較于采用小轉角假設的傳統有限元模型在瞬態響應計算及碰撞研究中具有明顯的優勢[5]。氣動力由準定常氣動模型計算得到，并計入所有剛體轉角及彈性變形的影響。由于尾跡模型對于揮舞彎矩的預測至關重要[6]，本文采用自由尾跡入流模型計算槳盤入流。剖面氣動力系數從翼型數據表中根據有效迎角與來流速度插值得到。離散后的氣動力以廣義力的形式表達，運動方程依據Hamilton原理推導建立。由于傳統積分方法對于瞬態響應積分收斂較慢以及力積分法會引入數值累積誤差，本文發展了一種新的基于Richardson外插技術的自適應變步長Legendre-Gauss數值積分算法，加速收斂速度，降低累積誤差。

1 運動方程及求解方法

1.1 坐標系

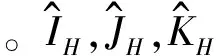
(1)

其中，u,v,w為槳葉在變形前坐標系中度量的彈性變形，η,ζ為質點位于剖面坐標系中的坐標。矢量在不同坐標系中的坐標可經由轉角余弦矩陣相互轉換得到。比如變形前坐標系中的矢量坐標經過轉換矩陣TDU轉到變形后坐標系中，即：rD=TDUrU，其中TDU是關于Euler角的函數矩陣。

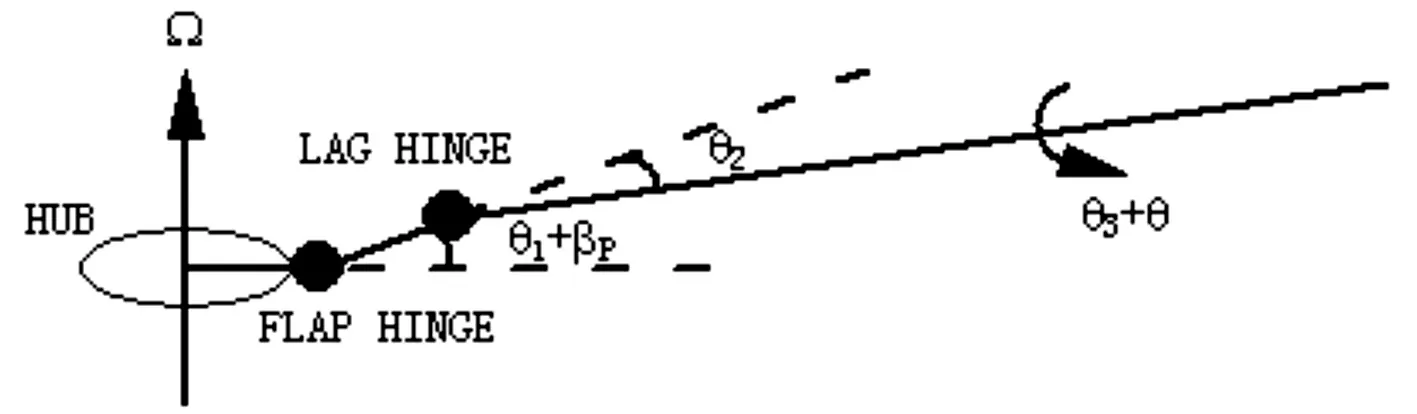
圖1 鉸與軸承的運動

為了充分考慮鉸接式旋翼槳葉在鉸及變距軸承處的慣性運動，引入三個剛體自由度，用以模擬鉸與軸承處的槳葉轉角，分別是剛體揮舞角(θ1+βp)、剛體擺振角(θ2)以及剛體變距角(θ3+θ0)，如圖1所示。βp指槳葉預錐角，θ0為操縱變距。θ1、θ2與θ3分別是因慣性力與外力綜合作用引起的揮舞鉸、擺振鉸以及變距軸承的剛體轉角。為方便列寫動能變分式，式(1)中的位置矢量通常需要經余弦轉換矩陣轉換到慣性系中。槳葉動能變分項最終由剖面動能變分沿槳葉展向積分得到：

(2)

勢能變分項由中等變形梁理論[7]推導得到。槳葉抽象為細長柔性Bernoulli梁，變形過程中剖面與槳葉參考軸線始終保持垂直，不計橫向剪切。為了更精確地對彈性扭轉建模，本文在勢能變分項推導中未使用階次準則。文獻[8]指出，保留彈性扭轉的高階項(三階或以上)對于保持力積分法與模態疊加法結果的一致性非常重要。

與傳統有限元建模方法不同，由于模型中剛柔耦合的存在，方程的建立與槳葉剖面振動載荷的計算需要作出相應的修改。氣動力虛功需要以對應于剛體自由度與彈性自由度的廣義力形式給出，因為它對剛體自由度同樣做功。外力變分項可寫成：

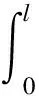
(3)

其中，R為質點在旋轉槳轂坐標系中的坐標；TRD是矢量從變形后坐標系到旋轉槳轂坐標系中的轉換矩陣，因此也是剛體轉角以及彈性變形的函數；φ為彈性扭轉角；Fa與Ma分別指變形后坐標系中的氣動力與力矩。實際計算中，它們不僅包含采用準定常氣動模型得到氣動環量力與力矩，還考慮了基于Greenberg薄板理論的非環量力與力矩分量。非環量部分是迎角變化率及彈性扭轉的函數，提供氣動阻尼，對氣彈響應計算中的數值穩定性至關重要。

1.2 動力學方程

在得到動能變分、勢能變分以及外力虛功后，槳葉非線性動力學微分方程組依據Hamilton原理建立起來。槳葉運動由形函數離散成廣義節點自由度q的形式(由剛體自由度與Chopra 15自由度[9]組成)。動力學方程的最終形式可表示為：

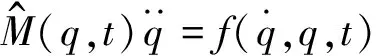
(4)

(5)

為避免Jacobi陣的求逆操作，通過求解關于方程單步迭代差值的線性方程組推進牛頓迭代算法[11]，減少了程序計算量。同時，修改的牛頓法只在程序開始時計算Jacobi陣并在隨后的迭代中當作常量處理；但在本文中為保證收斂方向，當收斂速度變慢時程序會適時更新Jacobi陣。

1.3 載荷計算方法

旋翼動力學中一般使用三種計算方法預測槳葉結構載荷。力積分法[1,8,12]將剖面結構載荷沿外段槳葉從計算參數點(即待求載荷的徑向位置)到槳尖積分得到參考點結構載荷。因而這種方法會累積所有可能的由數值算法或剖面特性差異引起的誤差。根據Hamilton原理與牛頓定律的等價性，槳葉慣性載荷可直接由動能變分對應的自由度變分分量得到[8]。即慣性載荷可表示為：

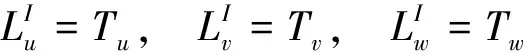
(6)

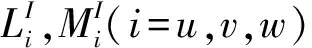
基于這種相對簡單的對應關系，求解動能變分中的非線性項TNL子函數可在力積分法計算載荷時被再次調用，極大地降低了載荷程序實現的復雜度。由于質量陣也來自于動能變分，一種新的計算慣性載荷的方法可以推導出來：

(7)

其中，Q是由所有槳葉運動自由度組成的列向量，在本文中寫成(θ1,θ2,θ3,u,v,w,φ,v′,w′)T的形式，二階導數為其對應加速度項；M為槳葉運動自由度對應的離散之前的質量陣；g為體現式(6)中關系的抽象函數。

力積分法計算中，外段剖面對計算參考點x0的彎矩包括兩部分：外段剖面力對計算參考點的力矩以及外段剖面內力對于本地軸線形成的彎矩；其中剖面力又由慣性載荷與氣動外力組成。最終彎矩沿槳葉展向積分得到。以變形前坐標系中的揮舞彎矩為例：

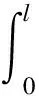
(8)

其中，Δw=w-w0, Δx=(x+u)-(x0+u0)，下標0表示該變量是對應于計算參考點處的運動變形。因為傳統Legendre-Gauss數值積分方法在有瞬態氣動力作用時收斂速度較慢，本文將Richardson外插技術與之結合，發展了一種新的數值積分算法，以加快積分的收斂速度并盡可能地減少累積誤差。

曲率法[2,4]的思想可以簡潔地解釋為彎矩只與梁的彎曲程度有關。該方法需要對槳葉彈性變形作二次偏導數，因而基于傳統模態法求解響應時須保留足夠多的模態才能達到合理的精度。本文采用隱式方法在位形空間中求解方程，因此不存在這種因模態截斷引起的問題。仍以揮舞彎矩為例：

(9)

其中，EIy為揮舞 剛度；EA為拉伸剛度；θt指剖面預扭角；eζ指剖面重心在剖面坐標系中擺振方向的偏移。值得注意的是，與式(8)不同，式(9)中的彎矩是在變形后坐標系中度量的；因此在與力積分法比較時，需要將二者的載荷矢量統一到同一坐標系中。由于飛行實測載荷數據是在變形后坐標系中得到的，實際計算時式(8)的結果同樣需要經過TDU轉換到變形后坐標系中，而式(9)則不必。

反力法[12]基于有限元原理，因此結果取決于動力學有限元建模的精度。在有限元組集過程中，節點內力在相鄰單元之間是相互抵消的；但在最終方程求解之后，由組集之前的相應單元矩陣形成的梁單元方程是非平衡系統，其余量即為相鄰單元作用于節點的結構載荷。反力法不能有效預測有限元非節點位置處的結構載荷。盡管如此，反力法仍是一種計算代價較小的載荷計算方法。節點反力可寫為：

(10)

其中，下標EL指該變量是原始單元矩陣或向量，并非直接取自方程組集之后的總體矩陣或向量。揮舞彎矩是Freaction中對應于w′自由度的分量，擺振彎矩即是對應于v′自由度的分量。類似的，反力法的載荷結果是在變形前坐標系中度量的，在與別的方法以及實驗結果比較時需要進行轉換。

2 算例與討論

采用BO105模型槳葉[13]作為第一個算例對比在無氣動外力作用下三種載荷計算方法的結果。BO105直槳葉安裝在無鉸式槳轂上。給定槳尖揮舞方向初速度10 m/s，徑向位置21.6%R處的揮舞彎矩、擺振彎矩以及扭轉彎矩分別如圖2/3/4 所示。可以看出，即使在這種劇烈振動狀態下，三種方法的結果仍能吻合得很好。這說明了三種方法在對于無鉸式旋翼槳葉純結構振動載荷具有相同的精度。

第二個算例采用SA349/2[15]直升機飛行實測載荷數據驗證三種載荷計算方法。SA349/2是裝有非線性減擺器的鉸接式旋翼，其槳葉具有先進幾何外形(預扭及非對稱翼型等)及非線性剖面特性(剖面重心偏置等)。選取試驗中的飛行狀態3 (μ=0.198,CT/σ=0.062) ，比較研究三種載荷計算方法。

圖2 揮舞彎矩，剖面位置21.6%R, BO105

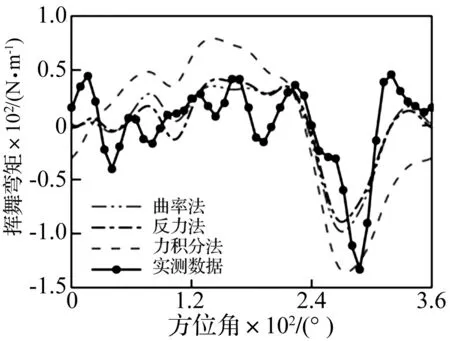
圖5 揮舞彎矩，剖面位置80%R, SA349/2

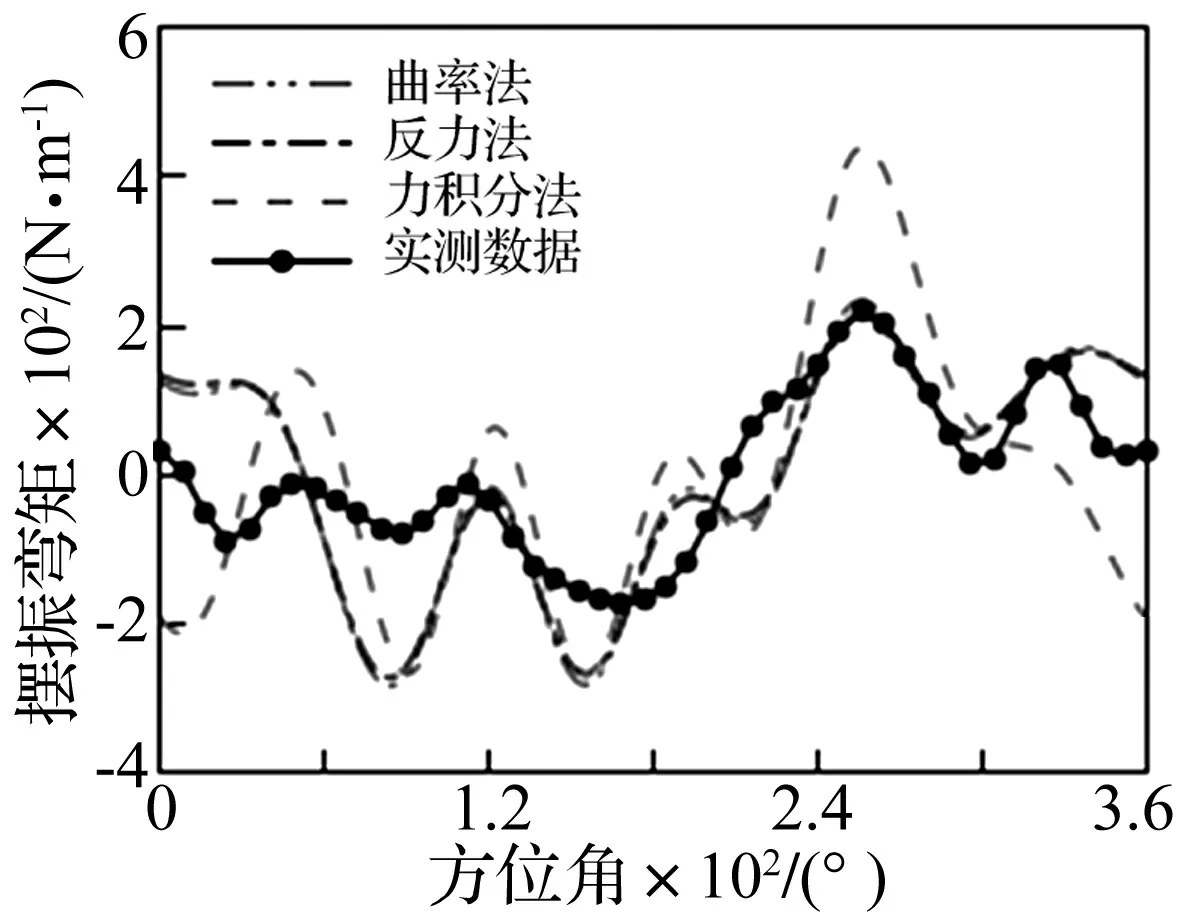
圖6 擺振彎矩，剖面位置46%R, SA349/2

徑向位置80%R處揮舞彎矩及46%R處擺振彎矩分別如圖5/6所示。三種方法都能預測到彎矩的大致趨勢。對于揮舞彎矩，力積分法在整個周期上都預測偏高；并且彎矩隨時間變化的曲線較平滑，相位細節有損失。這種預測偏高的現象同樣在擺振彎矩出現，如圖6所示。對于槳葉中段的擺振彎矩，曲率法與反力法都比力積分法獲得了更為合理的結果。在槳葉前進邊，三種方法都預測過高。除了線性當量阻尼模型對于非線性減擺器建模的不準確以外，準定常氣動模型可能不足以預測這種飛行狀態下槳葉前行邊氣動載荷的計算。因為中等前飛狀態下，槳渦干擾的存在降低了準定常氣動模型的氣動力預測精度。這種情況需要采用非定常氣動模型[4]或計算流體動力學模型對氣動力進行建模[8,15]。

3 結 論

本文建立了考慮剛體與彈性運動耦合的旋翼剛柔耦合動力學模型。依據Hamilton原理與牛頓定律的等價性，發展了一種易于實現的力積分方法。為加快積分收斂速度及減少積分誤差，開發了一種新的基于Richardson外推法的Legendre-Gauss數值積分算法。著重比較直升機常用的三種載荷計算方法，以無鉸式BO105模型槳葉以及鉸接式SA349/2直升機為研究對象，分析對比了三種載荷方法的預測精度與適應范圍。基于上述研究，本文總結如下：

(1) 在純結構系統給定初始仿真運動條件下，由于不考慮氣動力，三種載荷計算方法都能勝任結構振動載荷的預測，包括槳葉剖面揮舞彎矩、擺振彎矩及扭轉力矩。

(2) 曲率法與反力法易于實現。在有氣動外力作用條件下，二者較力積分法能獲得頻率更為豐富幅值更為合理的載荷結果。反力法無法預測有限元非節點處的結構載荷。依靠相鄰節點之間的形函數插值得到的載荷是不準確的，槳葉建模時需要人為添加有限元節點。

(3) 氣動模型對于旋翼振動載荷至關重要，氣動力的預測能力需要進一步提高。從對比結果看，三種載荷計算方法都未能準確預測槳盤前行邊的振動載荷，這與前行邊的槳葉剖面氣動力預測精確不夠有關。

參 考 文 獻

[1]Bialawa Richard L. Blade stress calculation-mode deflection vs. force integration[J]. Journal of the American Helicopter Society, 1978, 23(3),10-16.

[2]Maier T H. An examination of helicopter rotor load calculations[C]. The American Helicopter Society National Specialists’ Meeting on Rotorcraft Dynamics, Arlington, Texas, November 1989.

[3]Lim J W, Analytical investigation of UH-60A flight blade airloads and loads data[C]. The 51th Forum of the American Helicopter Society, Fort Worth, Texas, May 1995.

[4]WANG Hao-wen, GAO Zheng. Rotor vibratory load prediction based on generalized forces[J]. Chinese Journal of Aeronautics, 2004,17(1):28-33.

[5]韓東,高正，王浩文,等. 直升機槳葉剛柔耦合特性及計算方法分析[J]. 航空動力學報, 2006,21(1):36-40.

HAN Dong, GAO Zheng, WANG Hao-wen. Analysis of the computational method and the helicopter blade characteristics with coupled rigid and elastic Motions [J]. Journal of Aerospace Power, 2006,21(1):36-40.

[6]Bousman W G, Maier T H, An investigation of helicopter rotor blade flap vibratory loads[C]. The 48th Annual Forum of the American Helicopter Society, Washington, D.C., June 1992.

[7]Hodges D H, Dowell E H. Nonlinear equations of motion for the elastic bending and torsion of twisted nonuniform rotor blades[R]. NASA TN D-7818, December,1974.

[8]Datta A, Fundamental Understanding, Prediction and validation of rotor vibratory loads in steady level flight[D]. PhD thesis in Aerospace Engineering, 2004.

[9]Chopra I, Sivaneri N T, Aeroelastic stability of rotor blades using finite element analysis[R]. NASA-CR-166389, August 1982.

[10]虞志浩, 楊衛東, 張呈林. 基于Broyden法的旋翼多體系統氣動彈性分析[J]. 航空學報, 2012,33(12):2171-2182.

YU Zhi-hao, YANG Wei-dong, ZHANG Cheng-lin. Aeroelasticity analysis of rotor multibody system based on Broyden method[J]. Chinese Journal of Aeronautics, 2012,33(12):2171-2182.

[11]Ascher U M,Petzold L R. Computer methods for ordinary differential equations and differential-algebraic equations[M]. SIAM press, 1998.

[12]Floros M W, Elastically tailored composite rotor blades for stall alleviation and vibration reduction[D]. PhD thesis in Aerospace Engineering, December 2000.

[13]Bir G, Chopra I. University of maryland advanced rotorcraft code (UMARC) theory manual[M].Vol3.July 20, 1994.

[14]Heffernan R, Gaubert M, Structural and aerodynamic loads and performance measurements of an SA349/2 Helicopter with an Advanced Geometry Rotor[R]. NASA TM-88370, 1986.

[15]Abhishek A, Analysis, Validation, Prediction and fundamental understanding of rotor blade loads in an unsteady maneuver[D]. PhD thesis in Aerospace Engineering, 2010.