計電磁不平衡拉力的高速電主軸轉子偏心特性研究

陳小安， 張 朋， 陸永亞， 合 燁， 劉俊峰

(重慶大學 機械傳動國家重點實驗室，重慶 400044)

高速旋轉機械的高速電主軸轉子系統偏心狀態會引起主軸劇烈振動，不但影響數控機床加工精度，且會導致電主軸失效[1-2]。將轉子偏心引起的離心力載荷作為高速電主軸主要外載荷研究較多。Hongqi等[3-4]通過建立的高速電主軸熱-機耦合動力學模型，在對動力特性研究中發現，離心力載荷是轉子系統的重要外載荷。Jorgensen等[5-6]據影響系數法建立高速電主軸動力學模型，討論不同工況離心力載荷對轉子動力學行為響應。Nelson[7]用Timoshenko梁理論建立高速電主軸動力學模型，并詳細分析離心力載荷計算方法。

本文將高速電主軸轉子偏心狀態引起的另一重要載荷-電磁不平衡拉力考慮入轉子外載荷，分析兩種外載荷對轉子動態特性影響；計算軸承動態支撐剛度隨轉速的變化及對轉子系統一階固有模態影響；通過實驗進行理論分析驗證。

1 轉子偏心載荷模型

制造、裝配等誤差易導致高速電主軸轉子系統偏心。高轉速下轉子系統偏心狀態會產生附加載荷-電磁不平衡拉力載荷與離心力載荷。

1.1 電磁不平衡拉力載荷

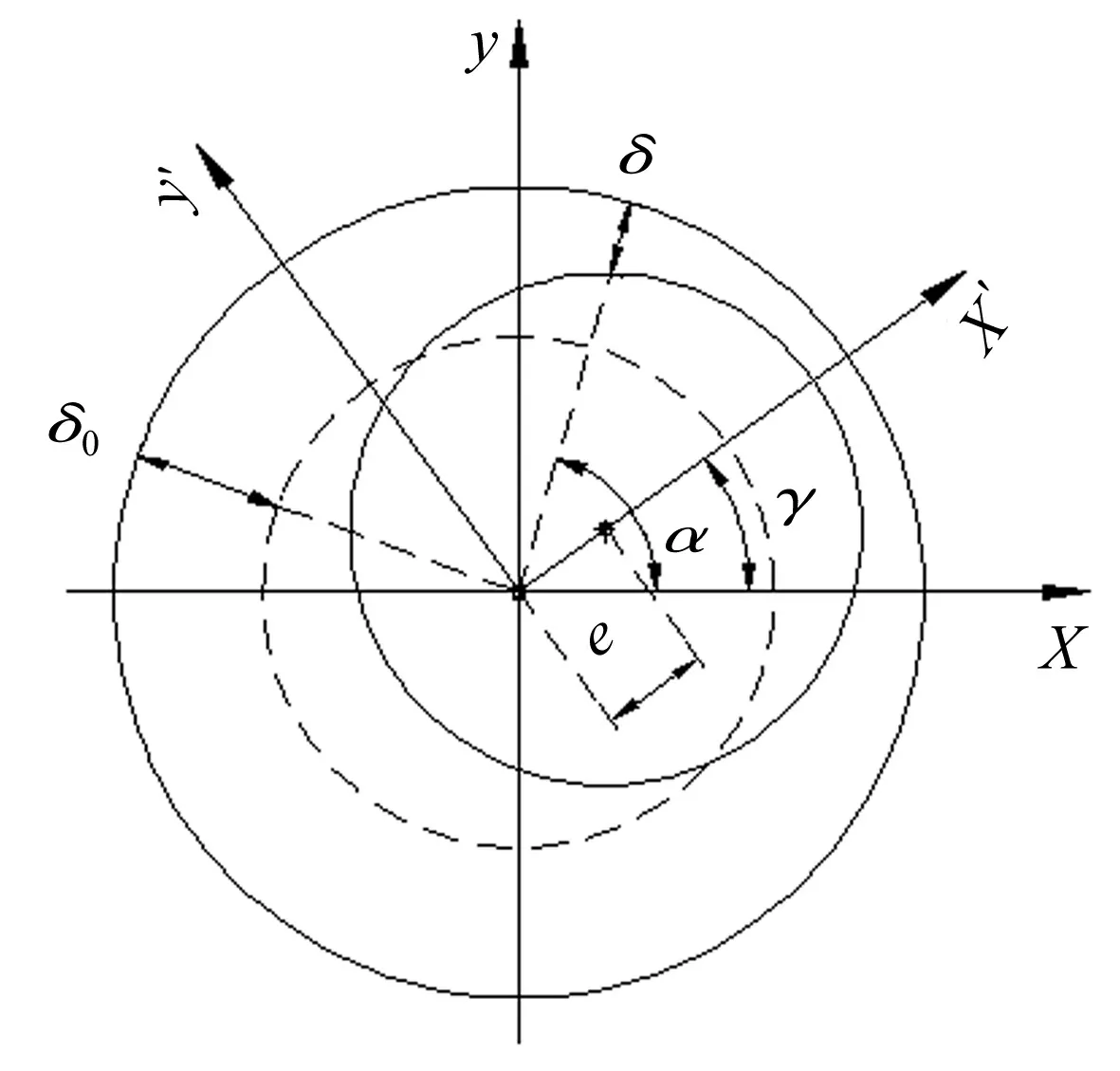
圖1 轉子偏心氣隙

高速電主軸轉子偏心時，電機定轉子不對心會造成氣隙磁場不均勻，導致轉子系統徑向附加磁拉力[8-9]。轉子偏心見圖1。圖1中δ為實際氣隙厚度；δ0為理想氣隙厚度；e為定轉子偏心距；α，γ分別為相互位置角。

實際氣隙厚度為：

δ=δ0-ecos(α-γ)

(1)

氣隙磁導為：

Λ=μ0/Kμδ

(2)

式中：μ0為空氣導磁系數；Kμ=(K1δ0+δFe)/K1δ0為氣隙飽和度，K1為平均氣隙系數，δFe為鐵磁材料當量氣隙。

氣隙合成磁動勢為：

F=FScos(ωSt-α)+FRcos(ωSt-α-φ)

(3)

式中：FS，FR為定子、轉子合成磁動勢幅值；ωS為電機同步角頻率；φ為轉子電流相對于定子電流滯后角。

氣隙磁密為：

B=ΛF

(4)

氣隙磁密切向分量遠小于徑向分量，可忽略不計，則轉子表面的麥克斯韋應力為：

σ=B2/2μ0

(5)

對轉子表面的麥克斯韋應力進行周向積分，可得轉子電磁不平衡磁拉力載荷幅值：

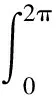
(6)

式中：R，L為電機轉子半徑、氣隙長度。電磁不平衡拉力角頻率與電機極對數無關，均為二倍轉頻[8]。

1.2 離心力載荷

轉子偏心質量造成的離心力載荷幅值與轉子轉速平方成正比[3-4]，其幅值為：

FC=mω2e

(7)

式中：m為轉子節點質量；ω為轉子轉頻。由于離心力載荷由轉子轉動引起，故其角頻率為一倍轉頻。

2 轉子動力學模型

高速電主軸為典型的軸承-轉子系統，考慮剪應變影響，用Timoshenko梁單元[10]耦合入軸承動態支承剛度[11]，對轉子系統進行動力學建模。

2.1 軸承動態支承剛度矩陣

高速運行的角接觸球軸承在軸向載荷Fa、徑向載荷Fr及彎矩載荷M的聯合作用下，內外圈會發生相對軸向位移δa、徑向位移δr及角位移θ，軸承內部幾何關系見圖2：E，E’，m，m’分別為軸承運行前后鋼球球心及內溝曲率中心；n為外溝曲率中心；α為鋼球原始接觸角；αij，αej分別為鋼球與內外圈實際接觸角；Rij為鋼球與內圈接觸半徑；Axj，Azj為任意鋼球位置Ψj處內溝曲率中心坐標；Vxj，Vzj為鋼球球心位置參數。

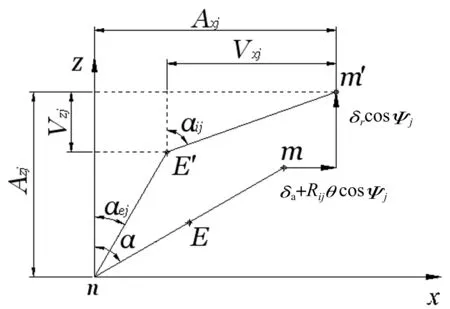
圖2 軸承內部幾何關系

據套圈控制理論及赫茲接觸理論[12]，聯立鋼球平衡方程與內圈平衡方程得軸承擬靜力平衡方程為：

Fb=Kbδb

(8)

式中：Fb為內圈載荷列向量；Kb為動態支承剛度矩陣；δb為軸承內圈位移列向量。

2.2 轉子動力學方程

耦合入軸承動態支承剛度矩陣，以電磁不平衡拉力與離心力為外載荷的高速電主軸轉子動力學方程為：

Ms{X″}+Cs{X′}+(Ks+Kb){X}={FM}+{FC}

(9)

式中：Ms，Cs，Ks分別為轉子質量矩陣、阻尼矩陣、剛度矩陣；{X″}，{X′}，{X}為節點加速度、速度、位移向量；{FM}，{FC}分別為電磁不平衡拉力載荷向量、離心力載荷向量。

3 仿真、實驗結果及分析

3.1 軸承動態支承剛度

本文以2GDZ15型高速電主軸為分析對象，其軸承型號為B7011CD/P4A，B7009CD/P4A。定位預緊，據生產廠的參數計算軸承動態支承剛度。由于軸承徑向剛度對轉子一階固有頻率影響較大，本文給出前后軸承四種轉速的徑向支承剛度，見圖3。由圖3看出，隨轉速的升高，定位預緊時角接觸球軸承徑向支承剛度隨之增大，且增幅較大。

圖3 軸承徑向支承剛度

圖4 轉子有限元模型

3.2 轉子動力學建模

2GDZ15型高速電主軸轉子系統有限元模型見圖4。轉子整體分為16個單元，17個節點；芯軸上附加轉動零件簡化成圓環；軸承支撐位于三角形處。

3.3 轉子模態仿真

據有限元法基本理論構建轉子動力學方程，用子空間迭代法求解一階模態。不同轉速的一階固有頻率見表1。

表1 轉子一階固有頻率

轉子一階固有振型為徑向振動，最大振幅出現在轉子尾部，其一階陣型見圖5。

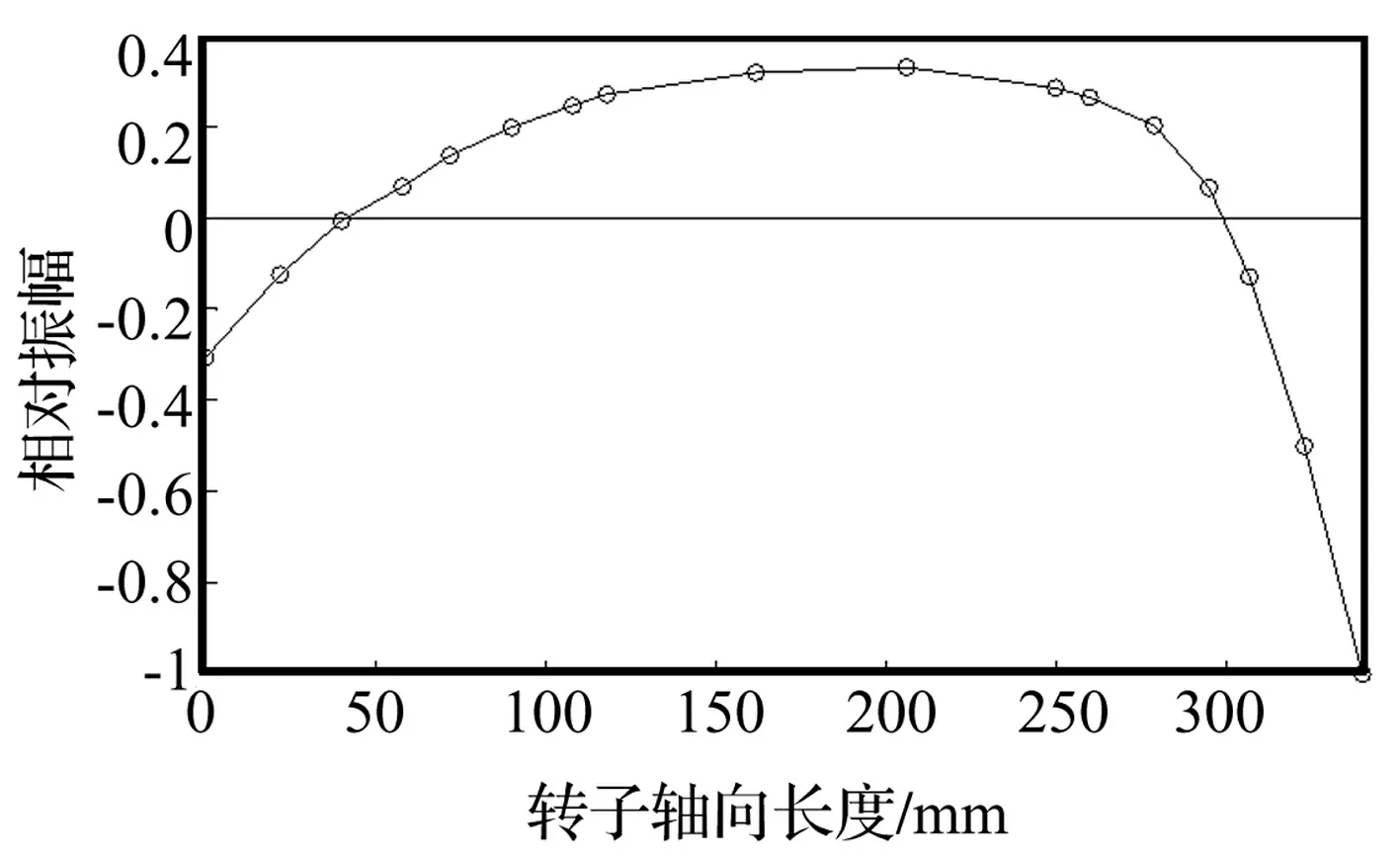
圖5 轉子一階固有振型

3.4 轉子振動實驗

實驗裝置包括2ZDG15型高速電主軸、WD501型電渦流式位移傳感器及前置器、B&K2692-014電荷放大器、SC305-UTP型數據采集分析儀及信號處理分析軟件。電主軸運行穩定后，用電渦流位移傳感器測量電主軸轉子前端徑向振動位移，采樣頻率4 096 Hz，采樣時間1 s。測試分析流程見圖6。

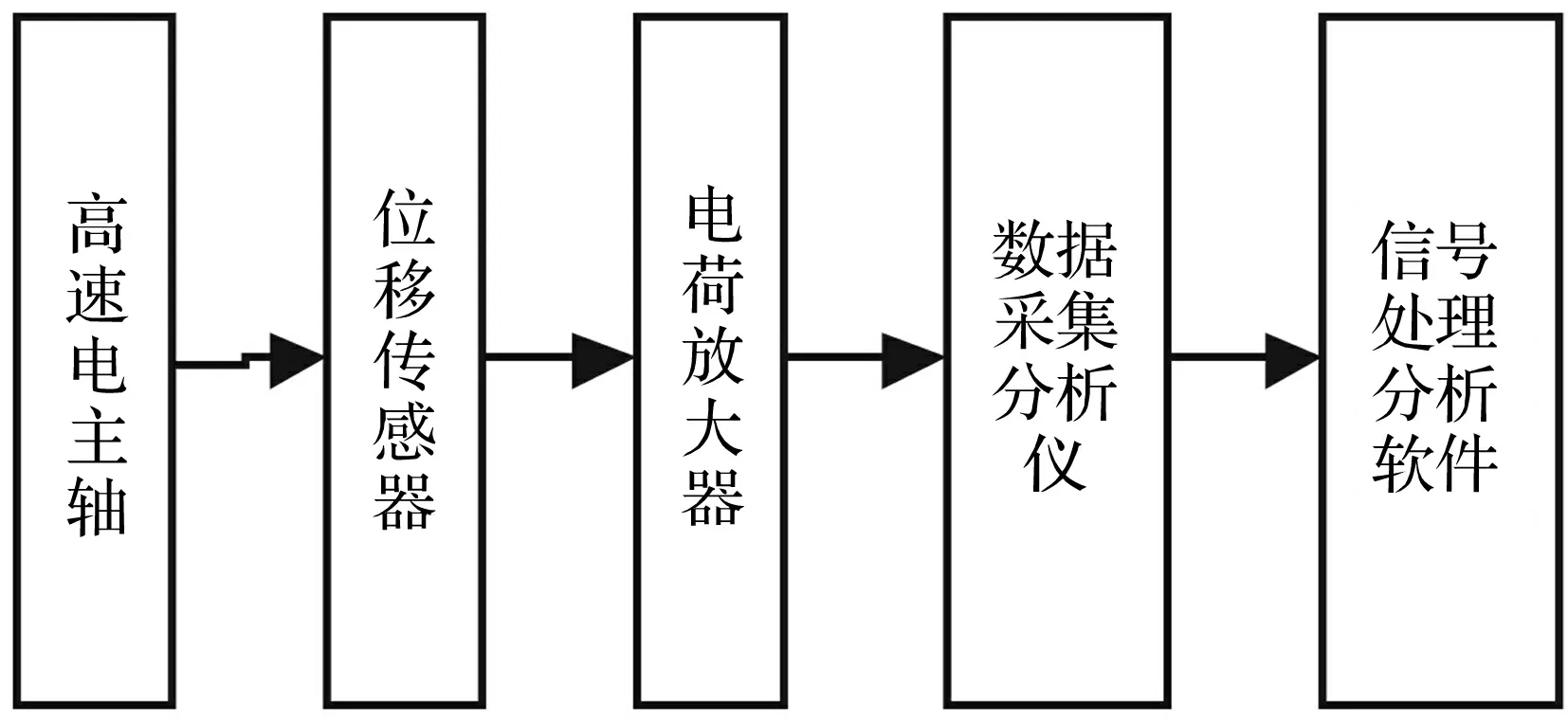
圖6 振動測試分析流程圖

3.5 試驗結果及分析

對位移振動信號進行頻譜分析，不同轉速的電主軸前端徑向位移振動信號頻譜見圖7。

圖7 振動信號頻譜圖

不同轉速時一、二倍轉頻處均出現振動峰值，分別對應轉子偏心引起的離心力載荷及電磁不平衡拉力載荷，說明兩種偏心載荷確為引起電主軸振動的重要激振力。隨轉速的升高，一、二倍轉頻處振動幅值隨之升高，導致偏心載荷增大，對應頻率處的振動幅值亦增大。由于噪聲信號影響，電主軸轉子一階固有頻率處產生的共振振幅值較大。但隨轉速的升高，一階固有頻率隨之升高，因為軸承徑向動態支承剛度隨轉速的增大而增大，導致轉子系統固有頻率隨轉速的升高而升高。計算結果與實驗相比，四種轉速時誤差分別為5.76%，5.33%，4.43%，3.88%。

4 結 論

(1) 高速電主軸轉子偏心會引起電磁不平衡拉力載荷與離心力載荷，隨轉速的升高，振動幅值增大，轉子偏心加劇，兩種載荷隨之增大。對轉子動態特性影響較大，振動頻譜對應頻率處均出現較大峰值。

(2) 由于噪聲信號影響，轉子一階固有頻率處產生共振，頻譜出現峰值；隨轉速的升高，軸承徑向動態支撐剛度增大，導致轉子系統一階固有頻率升高。

(3) 據2ZDG15型高速電主軸轉子偏心時載荷理論分析及振動實驗驗證，偏心載荷是電主軸振動的主要來源。高品質電主軸制造須進行嚴格動平衡，或設計在線動平衡調節裝置[13]，以保證電主軸轉子振動幅值在允許范圍內。

參 考 文 獻

[1]Abele E, Altintas Y, Brecher C. Machine tool spindle units [J]. CIRP Annals-Manufacturing Technology, 2010, 59(2):1-22.

[2]Jedrzejewski J, Kowal Z. High-speed precise machine tools spindle units improving[J]. Journal of Materials Processing Technology, 2005, 162-163: 615-621.

[3]Li H Q,Shin Y C.Integrated dynamic thermo-mechanical modeling of high speed spindles, part 1: model development [J]. Journal of Manufacturing Science and Engineering, Transactions of the ASME, 2004, 126(1):148-158.

[4]Li H Q,Shin Y C.Integrated dynamic thermo-mechanical modeling of high speed spindles, part 2: solution procedure and validations[J]. Journal of Manufacturing Science and Engineering, Transactions of the ASME,2004,126(1):159-168.

[5]Jorgensen B R, Shin Y C. Dynamics of machine tool spindle/bearing systems under thermal growth[J]. Journal of Tribology, ASME, 1997, 119(4): 875-882.

[6]Jorgensen B R, Shin Y C. Dynamics of machine tool spindle/bearing systems under thermal growth [J]. Journal of Manufacturing Science and Engineering, ASME, 1998, 120(4): 387-394.

[7]Nelson H D. A finite rotating shaft element using timoshenko beam theory[J]. Journal of Mechanical Design, ASME, 1980, 102(4):793-803.

[8]Guo D, Chu F, Chen D. The unbalanced magnetic pull and its effects on vibration in a three-phase generator with eccentric rotor[J]. Journal of Sound and Vibration,2002,254(2): 297-312.

[9]Im H, Yoo H H, Chung J. Dynamic analysis of a bldc motor with mechanical and electromagnetic interaction due to air gap variation[J]. Journal of Sound and Vibration,2011,330(8): 1680-1619.

[10]Han S M, Benaroya H, Wei T. Dynamics of transversely vibrating beams using four engineering theories[J]. Journal of Sound and Vibration, 1999, 225(5): 935-988.

[11]李松生, 陳曉陽, 張 鋼,等. 超高速時電主軸軸承的動態支承剛度分析[J].機械工程學報, 2006, 42(11): 60-65.

LI Song-sheng, CHEN Xiao-yang ZHANG Gang,et al. Analysis of dynamic supporting stiffness about spindle bearings at extra high-speed in electric spindles[J]. Chinese Journal of Mechanical Engineering, 2006, 42(11): 60-65.

[12]Jones A B. A general theory for elastically constrained ball and radial roller bearings under arbitrary load and speed conditions [J]. Journal of Basic Engineering, AMSE, 1960, 82(2):309-320.

[13]樊紅衛, 景敏卿, 劉 恒. 主動混合式砂輪-電主軸系統自動平衡裝置研究綜述[J]. 振動與沖擊, 2012, 31(5): 26-31.

FAN Hong-wei, JING Min-qing, LIU Heng. Review for studying on active hybrid auto-balancer of grinding wheel and motor spindle[J]. Journal of Vibration and Shock, 2012, 31(5): 26-31.