大規模動力系統高精度増維精細積分方法快速算法
吳澤艷, 王立峰, 武 哲,
(1.清華大學 航天航空學院, 北京 100084;2 北京航空航天大學 航空科學與工程學院, 北京 100191)
對線彈性結構動力學問題,較成熟、常用的時域積分方法有Newmark方法、Runge-Kutta方法。因計算穩定性及精度要求,此兩方法的積分步長均較小,計算量較大。文獻[1]提出的求解結構動力方程精細時程積分法求解線性齊次常微分方程,能獲得數值上逼近計算機精度的結果。而求解非齊次常微分方程,該方法需對方程系數矩陣求逆計算,當逆不存在時方法失效。
為充分發揮精細積分方法高精度功效,正致力于研究避免矩陣求逆的精細積分方法,發展方向為:
(1)研究Duhamel項積分方法。采用數值積分方法對Duhamel項進行積分。張森文等[2-3]利用辛普生積分公式、高斯積分公式求解Duhamel積分,在精細積分方法基礎上研究Duhamel項的精細積分方法。譚述君等[4-5]對非齊次項多項式、指數函數、正/余弦函數給出精確計算方法,獲得數值上逼近計算機精度結果。譚述君等[6]基于Duhamel項的精細積分方法,構造出求解非線性微分方程的數值算法。
(2)研究增維精細積分方法。顧元憲等[7-8]提出增維精細積分法。該方法可避免矩陣求逆,但增維后系數矩陣是時變的,只在時間步長非常小時方可近似為定常矩陣。文獻[9-12]分別將非齊次項用Taylor多項式、Laguerre多項式、Legendre多項式及Chebyshev多項式展開,再利用増維方法擴大系數矩陣,并用精細積分算法求解新的微分方程組,獲得較好計算結果。文獻[13]將増維精細積分方法用于非線性系統求解。
由于用増維精細積分方法時増維后系數矩陣是時變的,如果每次遞推計算前均需按精細積分法進行L=20次矩陣與矩陣相乘,計算量大,效率低,對大規模動力系統更是如此。因此需研究増維精細積分方法的快速算法。任偉等[14]提出將非齊次項作為常數時的快速算法。張繼峰等[15]在增維精細積分法基礎上對矩陣進行分塊計算,考慮非齊次項特點,減小矩陣維數,實現簡化計算。將非齊次項近似為多項式研究中,文獻[4]給出的遞推計算公式精度高、算法快速。文獻[16]以精細積分方法為基礎,利用大規模動力系統矩陣的稀疏性及動力物理特性,分析矩陣指數的特殊結構,并給出計算大規模動力系統矩陣指數及動力響應的高效率方法。為進一步提高計算精度,本文研究將非齊次項近似為高次多項式(以二次多項式為例)基于増維精細積分的快速算法,獲得與文獻[4]相同結果。該算法不依賴于方程的物理特性,且具有高精度。
1 精細積分方法[1]
考慮齊次線性常微分方程初值問題:
(1)
式中:A為n階常數矩陣;x為n維列向量。據常微分方程理論,式(1)的解為:
x=eA·tx0
(2)
令時間步長為τ,一系列等步長τ的時刻為:
t0=0,t1=τ, …,tk=kτ, …
則:
x(τ)=x1=Tx0,T=eAτ
(3)
及遞推公式:
xk=Txk-1
(4)
問題歸結為式(3)中T陣的計算。在較小時間間隔[tk-1,tk]內計算T陣:
(5)
其中:m=2L。若L=20,則m=1 048 576。令μ=τ/m,因τ很小,m很大,故μ很小。在μ區間段內,有:
eμA≈I+Aμ+(Aμ)2/2+(Aμ)3/6+(Aμ)4/24=I+Ta
(6)
其中:
Ta=Aμ+(Aμ)2/2+(Aμ)3/6+(Aμ)4/24
(7)
令:
T=eτA=(I+Ta)2L=(I+Ta)2L-1(I+Ta)2L-1
(8)
且(I+Tb)(I+Tc)=I+Tb+Tc+TbTc,因此求解T即等同于執行語句為:
for(i=1;i<=L;i++)Ta=2Ta+TaTa
循環結束時執行:
T=I+Ta
(9)
由此獲得T陣。此即求解齊次常微分方程組初值問題的精細積分方法。
2 高精度増維精細積分方法快速算法
設系統剛度矩陣、阻尼矩陣、質量矩陣分別為k,C,M,則結構動力學方程為:
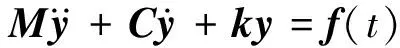
式中:f(t)為外力。方程可改寫為:
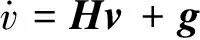
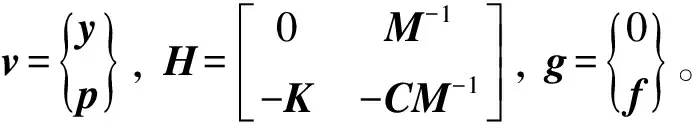
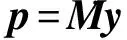
考慮初始條件的結構動力學方程可寫為:
(10)
式中:H為n階常數矩陣;g僅為時間t的函數。
將g在時刻tk處作Taylor展開:
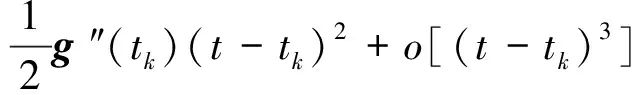
(11)
略去式(11)中高階項后代入式(10)得:
(12)
式中:
(13)
g0=g(tk),g1=g′(tk),g2=g″(tk)
式(12)在形式上表現為線性齊次常微分方程組,可用精細積分方法求解。但在不同時間段內矩陣A不同,若每次按精細積分法做L=20次矩陣與矩陣相乘,計算量較大,效率較低。以下導出求解矩陣Ta的快速算法。
由式(12)中矩陣A的定義計算得:
記:
P0=μI+(μ2/2)H+(μ3/6)H2+(μ4/24)H3
(14a)
Q0=(μ2/2)I+(μ3/6)H+(μ4/24)H2
(14b)
R0=(μ3/6)I+(μ4/24)H
(14c)
a0=μb0=μ2/2c0=μ
(14d)
由(7)式有:
(15)
執行一次Ta=2Ta+TaTa計算得:
(16)
式中:
(17)
比較式(15)、(16)可知,每執行一次更新計算所得新矩陣Ta形式不變。由此得計算Ta的快速算法:
(18)
式(18)循環結束后,得:
(19)
從而有:
vk+1=(PLH+In×n)vk+PLg0+QLg1+RLg2
(20)
式(20)即將非齊次項近似為二次多項式后的遞推計算公式。遞推計算前,先計算PL,QL,RL,PLH并保存。同文獻[4],乘法計算量亦為4L次矩陣與矩陣相乘。此后的每個時間步,每次遞推計算只需4次矩陣與向量相乘運算,避免L=20次矩陣與矩陣相乘,計算量由L(n+3)3減小到4n2,效率提高顯著。其中n為矩陣H的階數。若需進一步提高計算精度,可保留式(11)中更多Taylor展開項,亦能獲得類似結果。
3 算例
3.1 算例1
考慮動力系統:
其中:
記:
(i=1,2,…,n)
Φ(t)=[eλ1tr1, …, eλntrn]
f(t)=Φ(t)[1, …, 1]T
由于λi,ri為矩陣H的特征值及特征向量,故方程有解析解為:
x(t)=Φ(t)(t-t0)[1, …, 1]T
式中:n代表方程組規模。
取a=b=1.0,c=-2.0,Δt=0.01,n=100。為顯示算法的精度,在每個時間段分別將非齊次項近似為常數及一、二次多項式,遞推計算100步,相對誤差見圖1。由圖1看出,計算精度隨近似階的提高顯著提高。
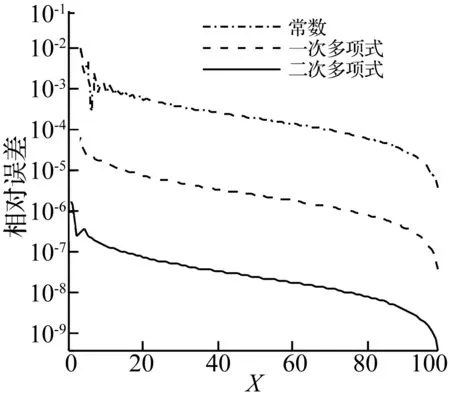
圖1 相對誤差
為顯示快速算法的高效性,分別用MATLAB的ode45函數、經典増維精細積分法與快速算法求解該動力系統。ode45基于Runge-Kutaa法,可自適應調節步長,精度設置為10-7。經典増維精細積分法與快速算法均將非齊次項近似為二次多項式,時間步長為0.01。計算規模n取不同值時用三種方法在時間方向遞推計算1 s的耗時見表1。其中快速算法的準備時間指遞推前計算式(20)中各矩陣的時間。由表1看出,隨計算規模的增大,與經典増維精細積分算法相比,快速算法的計算時間呈量級減少;快速算法耗時主要集中在遞推計算前的數據準備階段,計算時間少于ode45。因此推進計算時間越長,快速算法的優越性越顯著。
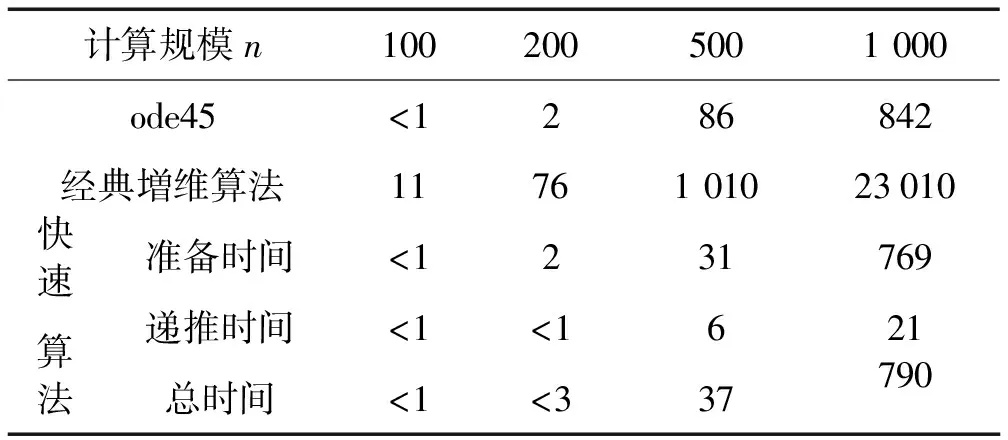
表1 計算時間對比(單位 s)
3.2 算例2[4]
設弦的張力為T,用4n+3個節點將弦等分為(4n+3)+1段,每個節點布置一個質量m/(4n+3),不計弦自重;在弦的1/4、1/2、3/4處分別受正/余弦函數形式的外部激勵,見圖2。
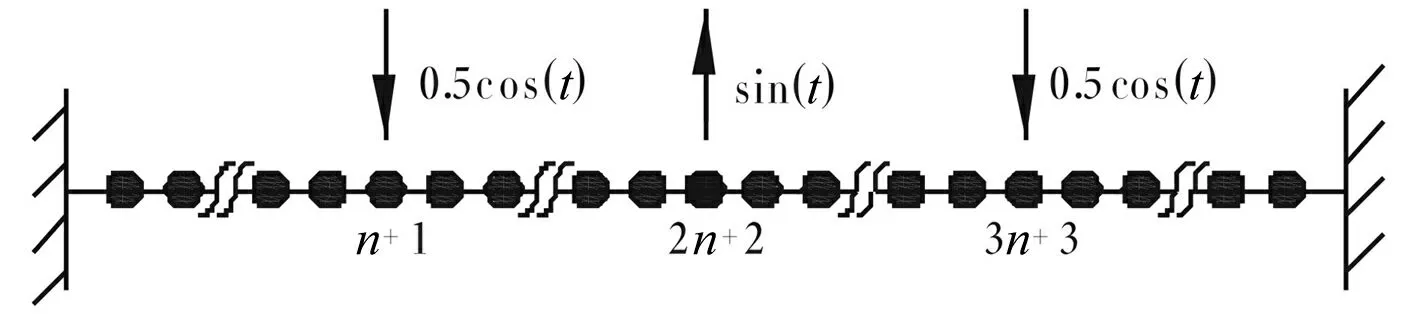
圖2 振動模型
記k=T/L,振動方程為:
其中:系統參數為:
參數k=2,m=1,ω=3,系統初始值為:
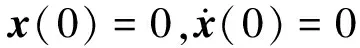
將方程降階后獲得與式(10)相同形式:
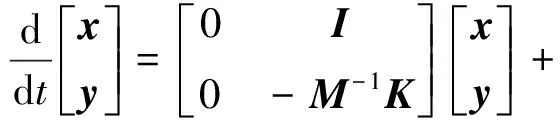
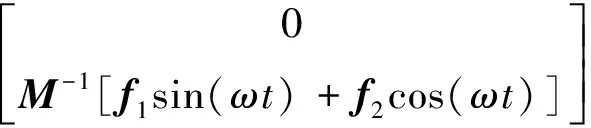
上式初始條件為:x(0)=0,y(0)=0。
為顯示算法精度,在每個時間段分別將非齊次項近似為常數及一、二次多項式,取Δt=0.01,n=10,遞推計算100步,以常微分方程組的小步長精細積分解為參考計算各算法誤差:
該參考解精度已達10-15量級。各算法絕對誤差見圖3。由圖3看出,計算精度隨近似階的提高顯著提高。
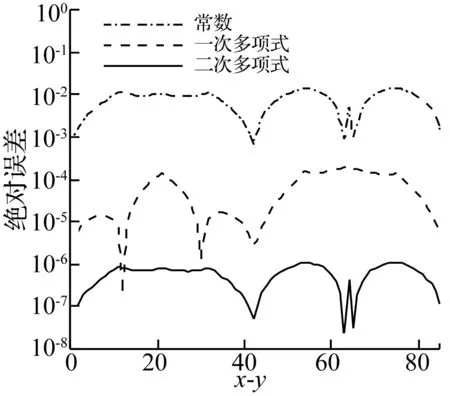
圖3 絕對誤差
為顯示快速算法的高效性,分別用MATLAB的ode45函數、經典増維精細積分法與快速算法求解該動力系統。ode45精度設置為10-6。經典増維精細積分法與快速算法均將非齊次項近似為二次多項式,時間步長為0.01。表2為n(計算規模為2(4n+3))取不同值時用三種方法在時間方向遞推計算5 s的時間消耗。由表2可得與算例1相同結論。若時間方向遞推時間少于5 s,則ode45計算時間少于快速算法。限于篇幅,不進行時間對比。因此,快速算法適合大規模動力系統長時間遞推計算。
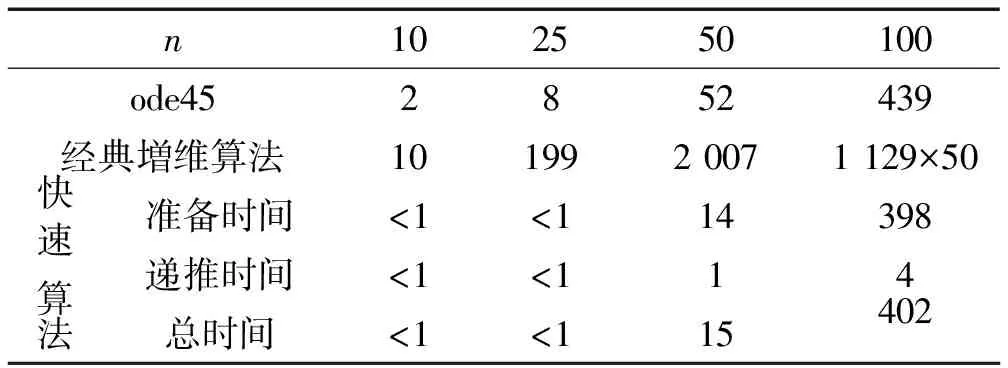
表2 計算時間對比(單位 s)
4 結 論
(1)本文通過將非齊次項近似為關于時間的高階多項式,形成高精度増維精細積分方法,提高増維精細積分方法求解動力系統精度;推導出高精度増維精細積分方法的快速算法計算公式,獲得與已有文獻相同結果。快速算法與動力系統物理特性無關,具有一般性。
(2)通過求解計算規模可調節的動力學問題,對比MATLAB ode45、快速算法與經典増維精細積分方法計算時間表明,所提快速算法具有高精度性、高效性,適合大規模結構動力學問題長時間推進計算。
參 考 文 獻
[1]鐘萬勰.結構動力方程的精細時程積分法[J].大連理工大學學報,1994,34(2):131-136.
ZHONG Wan-xie. On precise time-integration method for structural dynamics[J]. Journal of Dalian University of Technology, 1994,34(2):131-136.
[2]張森文,曹開彬.計算結構動力響應的狀態方程直接積分法[J].計算力學學報,2000,17(1):94-97.
ZHANG Sen-wen, CAO Kai-bin. Direct integration of state equation method for dynamic response of structure[J]. Chinese Journal of Computational Mechanics,2000,17(1): 94-97.
[3]汪夢甫,周錫元.結構動力方程的高斯精細時程積分法[J].工程力學,2004,21(4):13-16.
JIANG Meng-fu,ZHOU Xi-yuan. Gauss precise time-integration of structural dynamic analysis[J]. Engineering Mechanics, 2004, 21(4):13-16.
[4]譚述君,鐘萬勰.非齊次動力方程Duhamel項的精細積分[J].力學學報,2007,39(3):374-381.
TAN Shu-jun, ZHONG Wan-xie. Precise integration method for Duhamel terms arising form non-homogenous dynamic systems[J]. Acta Mechanica Sinica, 2007,39(3):374-381.
[5]富明慧,劉作秋,林敬華.一種廣義精細積分法[J].力學學報,2007,39(5):672-677.
FU Ming-hui, LIU Zuo-qiu, LIN Jing-hua. A generalized precise time step integration method[J]. Acta Mechanica Sinica, 2007, 39(5):672-677.
[6]譚述君,高 強,鐘萬勰.Duhamel項的精細積分方法在非線性微分方程數值求解中的應用[J].計算力學學報,2010,27(5):752-758.
TAN Shu-jun, GAO Qiang, ZHONG Wan-xie. Applications of Duhamel term’s precise integration method in solving nonlinear differential equations[J].Chinese Journal of Computational Mechanics,2010,27(5):752-758.
[7]顧元憲,陳飚松,張洪武.結構動力方程的增維精細積分法[J].力學學報,2000,32(4):447-456.
GU Yuan-xian, CHEN Biao-song, ZHANG Hong-wu.Prcise time-integration with dimension expending method[J]. Acta Mechanica Sinica, 2000, 32(4):447-456.
[8]Gu Y X,Chen B S, Zhang H W,et al. Precise time-integration method with dimensional expanding for structural dytlanlic equations[J].AIAA Journal, 2001, 39(12):2394-2399.
[9]向 宇,黃玉盈,黃健強.一種新型齊次擴容精細積分法[J].華中科技大學學報(自然科學版),2002,30(11):74-76.
XIANG Yu, HUANG Yu-ying, HUANG Jian-qiang. A method of homo-genization of high precision direct integration[J]. Journal Huazhong Univ. of Sci. & Tech. (Nature Science Edition), 2002, 30(11):74-76.
[10]馮 鳳, 周 鋼.半無限時域上任意右端激勵的長效精細算法[J].上海工程技術大學學報, 2005,19(3):215-219.
FENG Feng, ZHOU Gang. Long acting HHPD with arbitrary right impetus in semi-infinitive time domain[J]. Journal of Shanghai University of Engineering Science, 2005,19(3):215-219.
[11]時小紅,周 鋼,付召華.基于Legendre多項式函數系的齊次擴容精細算法[J].計算力學學報,2005,22(3):355-338.
SHI Xiao-hong, ZHOU Gang, FU Zhao-hua. A homogeneous high precise direct integration based on Legendre polynomial series[J]. Chinese Journal of Computational Mechanics,2005,22(3):355-338.
[12]付召華,周 鋼,羅 順,等.基于Chebyshev多項式函數系的齊次擴容精細算法[J].東華大學學報,2006,32(2):46- 49.
FU Shao-hua,ZHOU Gang,LUO Shun,et al. A homogenized high precision direct integration based on Chebyshev polynomial series[J].Journal of Donghua University, 2006, 32(2):46-49.
[13]張素英, 鄧子辰.非線性動力方程的増維精細積分法 [J].計算力學學報,2003,20(4):421-426.
ZHANG Su-ying, DENG Zi-chen. Increment dimensional precise integration method for nonlinear dynamic equation [J]. Journal of Computational Mechanics, 2003,20(4):421-426.
[14]任 偉,杜鐵鈞.定常結構動力方程增維精細積分法求解的注記[J].杭州電子科技大學學報,2005,25(1):41-43.
REN Wei, DU Tie-jun. A note on increment dimensional precise integration method for invariant dynamic equation [J]. Journal of Hangzhou Dianzi University, 2005,25(1): 41-43.
[15]張繼鋒,鄧子辰.結構動力方程的増維分塊精細積分法[J].振動與沖擊,2008,27(12):88-90.
ZHANG Ji-feng, DENG Zi-chen. Dimensional increment and partitioning precise integration method for structural dynamic equation[J]. Chinese Journal of Vibration and Shock,2008,27(12):88-90.
[16]高 強,吳 鋒,張洪武,等.大規模動力系統改進的快速精細積分方法[J].計算力學學報,2011,28(4):493-498.
GAO Qiang, WU Feng,ZHANG Hong-wu, et al. A fast precise integration method for large-scale dynamic structures[J]. Chinese Journal of Computational Mechanics, 2011,28(4):493-498.

