基于遺傳算法的圓柱空腔吸聲覆蓋層參數(shù)優(yōu)化研究

陶 猛， 趙 陽(yáng)， 王廣瑋

(1.貴州大學(xué) 機(jī)械工程學(xué)院，貴陽(yáng) 550025；2.上海交通大學(xué) 機(jī)械系統(tǒng)與振動(dòng)國(guó)家重點(diǎn)實(shí)驗(yàn)室, 上海 200240)

在水下航行器表面敷設(shè)吸聲覆蓋層既可減小主動(dòng)聲吶探測(cè)回波，亦可降低自身噪聲的外輻射，作為提高水下航行器隱身性能的技術(shù)手段被廣泛采用。經(jīng)半個(gè)多世紀(jì)發(fā)展，吸聲覆蓋層研究已取得豐富成果，如共振空腔吸聲覆蓋層[1-3]、微粒復(fù)合吸聲覆蓋層[4-6]、夾芯復(fù)合吸聲覆蓋層[7]等。圓柱空腔吸聲覆蓋層為共振吸聲覆蓋層的一種，通常由內(nèi)部排列的周期性空腔粘彈性介質(zhì)形成，空腔的基本形狀為圓柱、圓臺(tái)或喇叭形等截面且隨厚度變化。對(duì)該結(jié)構(gòu)的吸聲覆蓋層研究方法有：① 基于粘彈性介質(zhì)中波傳播特性的解析計(jì)算方法[3,8-9]，其區(qū)別在于所得波傳播特性精確[3]或等效[8-9]；② 基于有限元的數(shù)值計(jì)算方法[1-2,10]。數(shù)值計(jì)算方法可計(jì)算相對(duì)復(fù)雜結(jié)構(gòu)，但物理意義不明確；解析方法雖物理意義明確，便于分析其本質(zhì)，但無(wú)法計(jì)算復(fù)雜的聲學(xué)結(jié)構(gòu)。

吸聲覆蓋層的機(jī)理分析及聲學(xué)特性計(jì)算雖有較多研究成果，但對(duì)吸聲覆蓋層優(yōu)化設(shè)計(jì)研究較少。吸聲覆蓋層設(shè)計(jì)涵蓋材料、結(jié)構(gòu)、工藝等多方面，主要技術(shù)為聲學(xué)設(shè)計(jì)，即對(duì)吸聲覆蓋層基底材料及空腔結(jié)構(gòu)設(shè)計(jì)、優(yōu)化。吸聲覆蓋層優(yōu)化設(shè)計(jì)即通過(guò)合適的優(yōu)化算法合理設(shè)計(jì)吸聲覆蓋層結(jié)構(gòu)尺寸與材料參數(shù)，使吸聲覆蓋層達(dá)到最優(yōu)降低反射系數(shù)要求。但目前研究成果多集中于單個(gè)結(jié)構(gòu)參數(shù)或單個(gè)材料參數(shù)[3,6,10]對(duì)吸聲性能影響規(guī)律，而多參數(shù)同時(shí)變化進(jìn)而改變吸聲性能研究成果較缺乏。由于吸聲覆蓋層聲學(xué)性能與材料屬性、結(jié)構(gòu)參數(shù)呈非線性復(fù)雜關(guān)系，不適用經(jīng)典的搜索算法。隨計(jì)算機(jī)性能提高及現(xiàn)代優(yōu)化算法如遺傳算法、模擬退火算法等發(fā)展，使建立合理有效的吸聲覆蓋層材料及結(jié)構(gòu)參數(shù)綜合優(yōu)化方法成為可能。

本文對(duì)圓柱空腔吸聲覆蓋層的二維理論模型進(jìn)行簡(jiǎn)化，以獲得能快速準(zhǔn)確計(jì)算吸聲覆蓋層聲學(xué)性能的簡(jiǎn)化模型。并結(jié)合遺傳算法，通過(guò)對(duì)吸聲覆蓋層基底介質(zhì)材料參數(shù)及空腔結(jié)構(gòu)的優(yōu)化分析，建立圓柱空腔吸聲覆蓋層材料與結(jié)構(gòu)參數(shù)的綜合優(yōu)化設(shè)計(jì)方法。

1 吸聲覆蓋層聲學(xué)特性簡(jiǎn)化模型

圓柱空腔吸聲覆蓋層結(jié)構(gòu)沿厚度方向形成空腔，其基本形狀為圓柱型或圓臺(tái)形，見(jiàn)圖1(a)，按正三角形周期性排列相同空腔。因?qū)ΨQ性只取其中一個(gè)單元分析。由于建立六面棱柱體理論模型較困難，故用圓柱代替簡(jiǎn)化模型的復(fù)雜性，見(jiàn)圖1(b)。

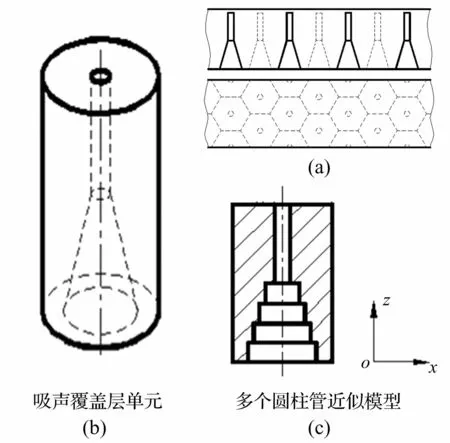
圖1 典型圓柱空腔吸聲覆蓋層及單元結(jié)構(gòu)示意圖

湯渭霖等[3,11]建立的圓柱空腔吸聲覆蓋層二維理論將吸聲覆蓋層模型簡(jiǎn)化為截面連續(xù)變化的多個(gè)粘彈性圓柱管組合，其聲學(xué)特性由波在圓柱管中傳播、損耗特性決定。但該模型因考慮高階軸對(duì)稱波對(duì)聲學(xué)特性的貢獻(xiàn)，使計(jì)算分析過(guò)程復(fù)雜繁瑣。因此，需基于二維理論尋找合理快速的近似方法，該方法主要基于兩個(gè)近似：①平面波垂直入射時(shí)，吸聲覆蓋層低頻性能由粘彈性圓柱管中最低階軸對(duì)稱波傳播特性決定[11]，進(jìn)而粘彈性圓柱管等效阻抗由最低階軸對(duì)稱波傳播波數(shù)確定。②對(duì)圓柱-圓臺(tái)空腔，近似為截面階梯變化的多個(gè)圓柱管組合，見(jiàn)圖1(c)，每段圓柱管有等效阻抗，整個(gè)圓柱管可視為多個(gè)阻抗變化的傳輸線組合。

平面波垂直入射時(shí)，吸聲覆蓋層中軸對(duì)稱波傳播特性可通過(guò)求解軸對(duì)稱波的特征方程獲得，即：

(1)

其中：

(2)

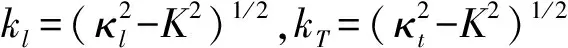
式(1)的詳細(xì)建立過(guò)程見(jiàn)文獻(xiàn)[3]。對(duì)給定的結(jié)構(gòu)參數(shù)及材料屬性，求解式(1)可得一組復(fù)根Km(m=1,2,…)，并由此確定kl,m，kt,m。此求解在復(fù)平面進(jìn)行，K的實(shí)部為傳播常數(shù)，虛部反映傳播衰減。

二維理論給出吸聲覆蓋層單元-粘彈性圓柱管中位移、應(yīng)力表達(dá)式[3]：

(3)

其中：RΦ,m為聲波在吸聲覆蓋層后端面(z=0)即背襯反射系數(shù);下標(biāo)m表示第m階軸對(duì)稱波傳播模式，j表示圓柱管截面第j圓環(huán)區(qū)域，m=j為能計(jì)算吸聲覆蓋層反射系數(shù)或吸聲系數(shù)的必要條件。式(3)中ζmj(V)，ζmj(W)為關(guān)于吸聲覆蓋層結(jié)構(gòu)、材料的復(fù)雜函數(shù)，即：

(4)

其中：αA,m,αB,m,αC,m為式(1)的代數(shù)余子式。參數(shù)V,W可表示為：

(5)

當(dāng)僅考慮最低階軸對(duì)稱波(m=j=1)時(shí)，粘彈性圓柱管的等效阻抗可寫(xiě)為：

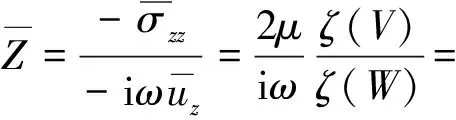
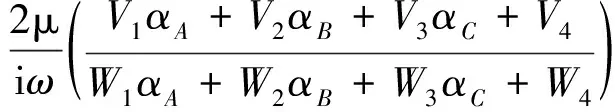
(6)

經(jīng)推導(dǎo)、簡(jiǎn)化，式(6)可寫(xiě)成簡(jiǎn)單形式：

(7)

至此，粘彈性圓柱管前端面(z=H，上標(biāo)f表示)、后端面(z=0，上標(biāo)b表示)處位移及應(yīng)力可通過(guò)傳遞矩陣T相聯(lián)系，即：

(8)

總傳遞矩陣可寫(xiě)成每段圓柱管傳遞矩陣的連乘形式：

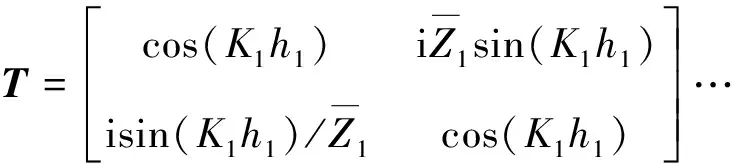
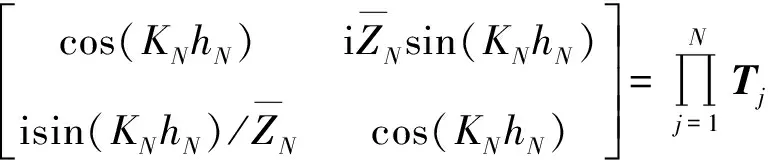
(9)

當(dāng)粘彈性圓柱管后端面(背襯)的阻抗Zb已知時(shí)，前端面表面阻抗可由式(8)獲得：

(10)

吸聲覆蓋層反射系數(shù)可寫(xiě)成：

(11)

式中：Zw為水介質(zhì)特性阻抗。

2 基于遺傳算法的吸聲覆蓋層參數(shù)優(yōu)化

由以上推導(dǎo)看出，吸聲覆蓋層反射系數(shù)或吸聲系數(shù)為關(guān)于基底介質(zhì)材料屬性及結(jié)構(gòu)參數(shù)的復(fù)雜函數(shù)，單純優(yōu)化吸聲覆蓋層結(jié)構(gòu)參數(shù)或材料屬性，難在寬頻范圍內(nèi)具備較高吸聲系數(shù)，而二者同時(shí)優(yōu)化則可能實(shí)現(xiàn)寬頻吸聲目標(biāo)。吸聲覆蓋層結(jié)構(gòu)參數(shù)包括穿孔率、空腔高度等；材料參數(shù)包括基底介質(zhì)密度、泊松比、楊氏模量及損耗因子等。而楊氏模量及損耗因子大小與頻率有關(guān)，較難用傳統(tǒng)的搜索算法解決。因此本文用遺傳算法進(jìn)行吸聲覆蓋層多目標(biāo)參數(shù)優(yōu)化研究。

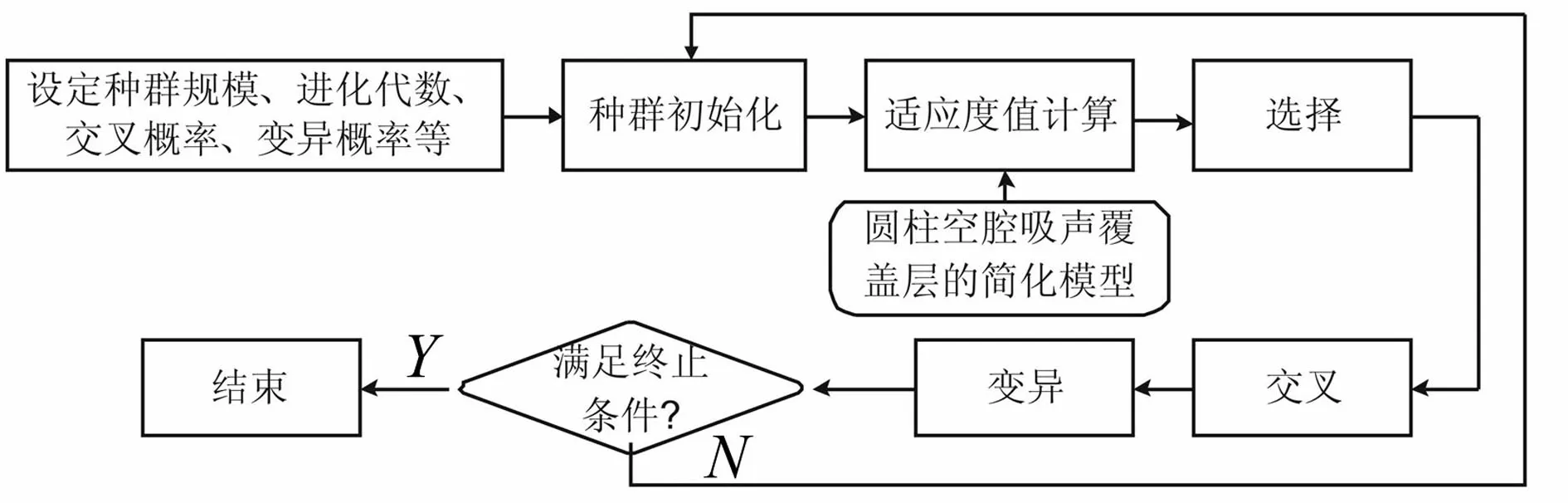
圖2 遺傳算法流程圖

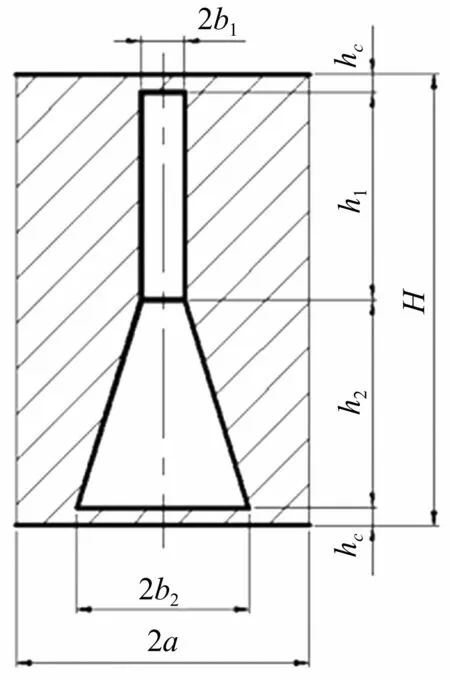
圖3 圓柱-圓臺(tái)空腔吸聲覆蓋層單元結(jié)構(gòu)示意圖

與傳統(tǒng)優(yōu)化方法相比，遺傳算法、模擬退火算法等在解決大規(guī)模非線性優(yōu)化問(wèn)題時(shí)優(yōu)勢(shì)明顯。其中遺傳算法為借鑒生物界自然選擇、自然遺傳機(jī)制的隨機(jī)搜索算法，較適用于處理傳統(tǒng)搜索算法難以解決的復(fù)雜、非線性優(yōu)化問(wèn)題。遺傳算法流程圖見(jiàn)圖2。遺傳算法由隨機(jī)產(chǎn)生的初始解開(kāi)始搜索，通過(guò)選擇、交叉、變異操作逐步迭代產(chǎn)生新解。該算法優(yōu)點(diǎn)即將參數(shù)編碼成染色體后進(jìn)行優(yōu)化，而不針對(duì)參數(shù)本身，因而不受函數(shù)約束條件限制；搜索過(guò)程由解的一個(gè)集合開(kāi)始，而非單個(gè)個(gè)體，具有隱含并行搜索特性，可大大減少陷入局部最小的可能性，且計(jì)算時(shí)不依賴于梯度信息，不要求目標(biāo)函數(shù)連續(xù)可導(dǎo)，較適合求解傳統(tǒng)搜索算法難以解決的大規(guī)模、非線性組合優(yōu)化問(wèn)題。

用遺傳算法對(duì)圖3吸聲覆蓋層進(jìn)行優(yōu)化。該吸聲覆蓋層單元間按正三角形方式排列，據(jù)上述簡(jiǎn)化方式，每個(gè)單元可簡(jiǎn)化為半徑a的圓柱體，且每個(gè)單元中包含圓柱、圓臺(tái)兩段空腔結(jié)構(gòu)，圓柱空腔半徑及圓臺(tái)空腔上表面半徑均為b1，圓臺(tái)空腔下表面半徑為b2，圓柱空腔及圓臺(tái)空腔高度分別為h1，h2，空腔兩端均有厚度為hc的封口薄層，整個(gè)吸聲覆蓋層高度為H=h1+h2+2hc。平面波由圓柱空腔一側(cè)垂直入射到吸聲覆蓋層，吸聲覆蓋層背襯條件為絕對(duì)軟背襯。

用遺傳算法進(jìn)行優(yōu)化時(shí)，目標(biāo)函數(shù)選擇為：

(12)

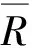
據(jù)遺傳算法理論，在MATLAB軟件中編寫(xiě)實(shí)現(xiàn)基本遺傳算法程序以尋找目標(biāo)函數(shù)最優(yōu)解。遺傳算法參數(shù)設(shè)置：種群規(guī)模100，進(jìn)化次數(shù)100，交叉概率0.8，變異概率0.2。

2.1 算例1(材料屬性優(yōu)化)

只優(yōu)化吸聲覆蓋層基底介質(zhì)的粘彈性動(dòng)態(tài)力學(xué)參數(shù)，即材料楊氏模量及損耗因子。由于粘彈性材料的動(dòng)態(tài)力學(xué)參數(shù)非常數(shù)，隨頻率變化呈色散關(guān)系，故假設(shè)粘彈性材料的楊氏模量及損耗因子隨頻率成二次函數(shù)關(guān)系[6]，即：

(13)

式中：f為頻率；E為楊氏模量(Pa)。若只考慮吸聲覆蓋層由一種基底介質(zhì)構(gòu)成，需優(yōu)化6個(gè)參數(shù)p0～p2，q0～q2。由此可計(jì)算不同頻率處的楊氏模量及損耗因子，進(jìn)而用簡(jiǎn)化模型計(jì)算反射系數(shù)。

經(jīng)優(yōu)化的6個(gè)參數(shù)及設(shè)定的覆蓋層單元各結(jié)構(gòu)參數(shù)見(jiàn)表1。“*”表示未優(yōu)化參數(shù)(下同)，在該算例中為單元各結(jié)構(gòu)參數(shù)。吸聲覆蓋層厚度H=50 mm。

表1 吸聲覆蓋層優(yōu)化后材料屬性及未優(yōu)化結(jié)構(gòu)參數(shù)

吸聲覆蓋層基底介質(zhì)的楊氏模量及損耗因子經(jīng)優(yōu)化的吸聲系數(shù)見(jiàn)圖4，經(jīng)優(yōu)化的楊氏模量及損耗因子見(jiàn)圖5。由圖4看出，吸聲覆蓋層最低吸聲頻率約2 kHz，在2～8 kHz頻率范圍內(nèi)，平均吸聲系數(shù)約0.86。

圖4 吸聲覆蓋層材料參數(shù)優(yōu)化后吸聲系數(shù)

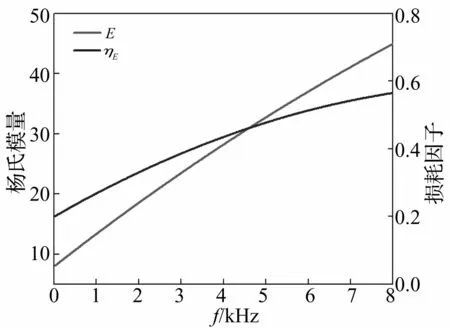
圖5 優(yōu)化后楊氏模量及損耗因子

2.2 算例2(材料屬性、結(jié)構(gòu)參數(shù)綜合優(yōu)化)

在算例1基礎(chǔ)上進(jìn)行材料屬性、結(jié)構(gòu)參數(shù)綜合優(yōu)化。待優(yōu)化結(jié)構(gòu)參數(shù)包括圓柱空腔半徑b1、圓臺(tái)下表面空腔半徑b2、圓柱空腔高度h1，圓臺(tái)空腔高度可據(jù)h2=H-h1-2hc計(jì)算獲得，而吸聲覆蓋層厚度H與封口薄層厚度hc設(shè)定不變。因此，待優(yōu)化參數(shù)包括與基底材料楊氏模量與損耗因子有關(guān)的6個(gè)系數(shù)、3個(gè)結(jié)構(gòu)參數(shù)計(jì)9個(gè)參數(shù)。

表2 吸聲覆蓋層優(yōu)化后材料屬性與結(jié)構(gòu)參數(shù)

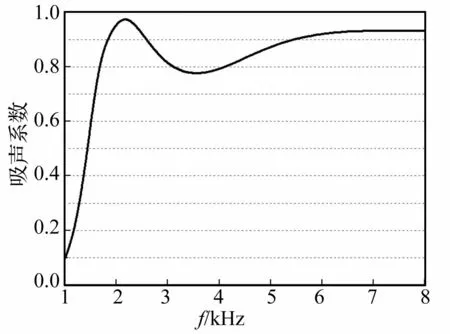
圖6 吸聲覆蓋層材料及結(jié)構(gòu)參數(shù)優(yōu)化后吸聲系數(shù)

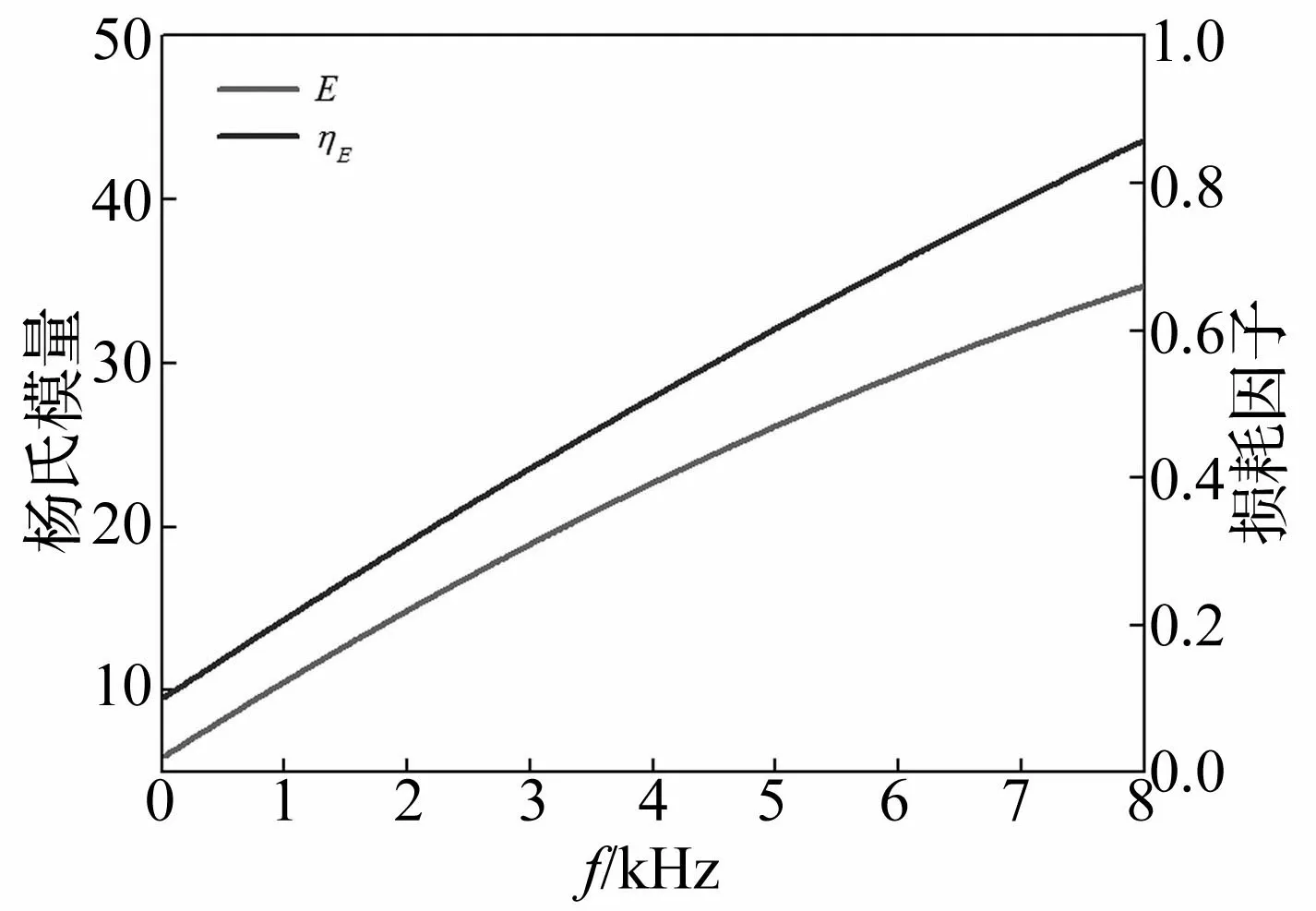
圖7 優(yōu)化后楊氏模量及損耗因子

經(jīng)優(yōu)化后9個(gè)參數(shù)及設(shè)定的其它結(jié)構(gòu)參數(shù)見(jiàn)表2，吸聲覆蓋層材料及結(jié)構(gòu)參數(shù)經(jīng)綜合優(yōu)化后吸聲系數(shù)見(jiàn)圖6，經(jīng)綜合優(yōu)化后基底介質(zhì)楊氏模量及損耗因子見(jiàn)圖7。由圖6看出，吸聲覆蓋層最低吸聲頻率仍為2 kHz左右，而在 2～8 kHz頻率范圍內(nèi)，平均吸聲系數(shù)約0.89。與算例1比較知，若同時(shí)優(yōu)化吸聲覆蓋層材料及結(jié)構(gòu)參數(shù)，可獲得吸聲性能更好的材料屬性與結(jié)構(gòu)參數(shù)組合。

2.3 算例3(兩層材料屬性及結(jié)構(gòu)參數(shù)綜合優(yōu)化)

考慮更復(fù)雜情況，設(shè)吸聲覆蓋層由兩種基底介質(zhì)構(gòu)成：包含圓柱空腔部分為第一種介質(zhì)，包含圓臺(tái)空腔部分為第二種介質(zhì)，即兩種介質(zhì)以圓柱空腔及圓臺(tái)空腔的交界處為邊界。需優(yōu)化的參數(shù)包括與第一種材料楊氏模量及損耗因子相關(guān)的6個(gè)系數(shù)(以上標(biāo)“(1)”表示)、與第二種材料楊氏模量及損耗因子相關(guān)的6個(gè)系數(shù)(以上標(biāo)“(2)”表示)、3個(gè)結(jié)構(gòu)參數(shù)計(jì)15個(gè)待優(yōu)化參數(shù)。

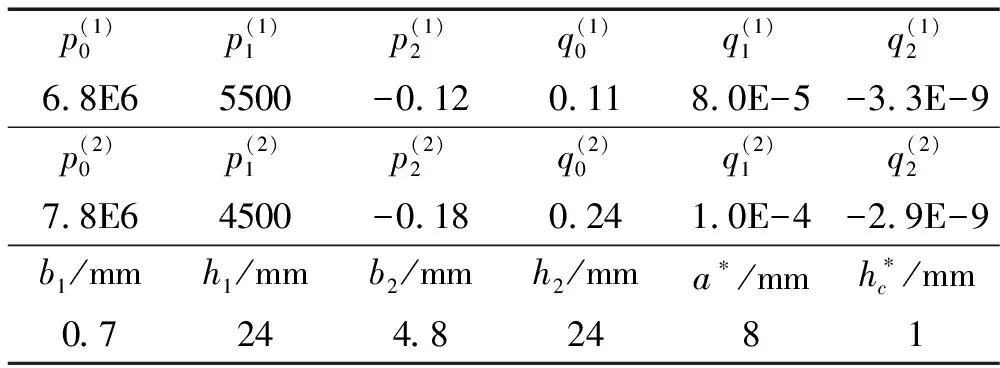
表3 吸聲覆蓋層優(yōu)化后兩層材料屬性及優(yōu)化后結(jié)構(gòu)參數(shù)

優(yōu)化后15個(gè)參數(shù)、設(shè)定的其它結(jié)構(gòu)參數(shù)見(jiàn)表3，吸聲覆蓋層,兩層材料屬性及結(jié)構(gòu)參數(shù)經(jīng)綜合優(yōu)化后吸聲系數(shù)見(jiàn)圖8，優(yōu)化后第一層介質(zhì)楊氏模量及損耗因子見(jiàn)圖9，優(yōu)化后第二層材料楊氏模量及損耗因子見(jiàn)圖10。由圖8看出，吸聲覆蓋層最低吸聲頻率略高于2 kHz, 在2～8 kHz頻率范圍內(nèi)，平均吸聲系數(shù)約0.93。與前兩種優(yōu)化模型相比，平均吸聲系數(shù)明顯提高，原因?yàn)榭紤]吸聲覆蓋層分層后，吸聲覆蓋層實(shí)現(xiàn)阻抗?jié)u變形式，使波在多層結(jié)構(gòu)中傳播時(shí)遭遇阻抗變化并發(fā)生多次反射、透射，模式轉(zhuǎn)換可產(chǎn)生更多的能量損耗，從而提高寬頻吸聲能力。而阻抗?jié)u變形式不僅可通過(guò)結(jié)構(gòu)分層實(shí)現(xiàn)，也可通過(guò)材料分層實(shí)現(xiàn)。

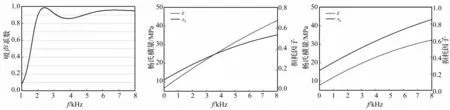
圖8 吸聲覆蓋層材料及結(jié)構(gòu)參數(shù)優(yōu)化后吸聲系數(shù)

3 結(jié) 論

(1) 圓柱空腔吸聲覆蓋層材料屬性與結(jié)構(gòu)參數(shù)存在一組使吸聲覆蓋層在工作頻段內(nèi)具有高吸聲系數(shù)的最佳值，該值可由參數(shù)優(yōu)化方法獲得。

(2) 較多需優(yōu)化參數(shù)尤其粘彈性材料動(dòng)態(tài)力學(xué)參數(shù)(楊氏模量、損耗因子)為頻率函數(shù)，常規(guī)搜索算法無(wú)法解決此類大規(guī)模非線性優(yōu)化問(wèn)題。

(3) 本文建立的圓柱空腔吸聲覆蓋層性能分析簡(jiǎn)化模型，通過(guò)用遺傳算法進(jìn)行吸聲覆蓋層材料屬性及結(jié)構(gòu)參數(shù)優(yōu)化分析，仿真算例表明，綜合優(yōu)化材料屬性及結(jié)構(gòu)參數(shù)可獲得更佳的寬頻吸聲性能。

(4) 本文所建優(yōu)化模型可進(jìn)行更多參數(shù)優(yōu)化分析，亦為吸聲覆蓋層優(yōu)化設(shè)計(jì)提供可行計(jì)算方法。

參 考 文 獻(xiàn)

[1]Hennion A C, Decarpigny J N. Analysis of the scattering of a plane acoustic wave by a doubly periodic structure using the finite element method: application to alberich anechoic coatings [J]. Journal of the Acoustical Society of America, 1991, 90(6):3356-3367.

[2]Easwaran V, Munjal M L. Analysis of reflection characteristics of a normal incidence plane wave on resonant sound absorbers: a finite element approach [J]. Journal of the Acoustical Society of America, 1993, 93(3):1308-1318.

[3]湯渭霖, 何世平, 范 軍. 含圓柱形空腔吸聲覆蓋層的二維理論[J]. 聲學(xué)學(xué)報(bào), 2005, 30(4):289-295.

TANG Wei-lin, HE Shi-ping, FAN Jun. Two-dimensional model for acoustic absorption of viscoelastic coating containing cylindrical holes [J]. Acta Acustica, 2005, 30(4): 289-295.

[4]Zhao H G, Liu Y Z, Wen J H, et al. Tri-component phononic crystals for underwater anechoic coatings[J]. Physics Letters A, 2007, 367(3): 224-232.

[5]Ivansson S M. Numerical design of alberich anechoic coatings with superellipsoidal cavities of mixed sizes[J]. Journal of the Acoustical Society of America, 2008, 124(4): 1974-1984.

[6]王仁乾, 馬黎黎. 吸聲材料的物理參數(shù)對(duì)消聲瓦吸聲性能的影響[J]. 哈爾濱工程大學(xué)學(xué)報(bào), 2004, 25(3): 288-294.

WANG Ren-qian, MA Li-li. Effects of physical parameters of the absorption material on absorption capability of anechoic tiles[J]. Journal of Harbin Engineering University, 2004, 25(3): 288-294.

[7]朱 錫, 羅 忠, 周 欣,等. 斜入射下水中隱身夾芯復(fù)合材料殼板結(jié)構(gòu)聲學(xué)設(shè)計(jì)[J]. 船舶力學(xué), 2009, 13(4): 646-656.

ZHU Xi, LUO Zhong, ZHOU Xin, et al. Acoustic stealth design on the underwater sandwich composite shell structure in oblique incidence [J]. Journal of Ship Mechanics, 2009, 13(4): 646-656.

[8]何祚鏞, 王 曼. 水下非均勻復(fù)合層結(jié)構(gòu)吸聲的理論研究[J]. 應(yīng)用聲學(xué), 1996, 15(5):12-19.

HE Zuo-yong, WANG Man. Investigation of the sound absorption of non-homogeneous composite multiple-layer structures in water [J]. Applied Acoustics, 1996, 15(5): 12-19.

[9]朱蓓麗, 任克明. 等效參數(shù)法研究帶圓柱通道橡膠體的聲學(xué)性能[J]. 上海交通大學(xué)學(xué)報(bào), 1997, 31(7): 20-24.

ZHU Bei-li, REN Ke-ming. Acoustic properties analysis of elastomer with cylindrical bores using equivalent parametric method [J]. Journal of Shanghai Jiaotong University, 1997, 31(7): 20-24.

[10]Panigrahi S N, Jog C S, Munjal M L. Multi-focus design of underwater noise control linings based on finite element analysis[J]. Applied Acoustics, 2008, 69(12): 1141-1153.

[11]何世平, 湯渭霖, 何 琳,等. 變截面圓柱形空腔覆蓋層吸聲系數(shù)的二維近似解[J]. 船舶力學(xué), 2006, 10(1): 120-127.

HE Shi-ping, TANG Wei-lin, HE Lin, et al. Analysis of acoustic characteristics of anechoic coating containing varying sectional cylindrical cavity [J]. Journal of Ship Mechanics, 2006, 10(1): 120-127.