軸向運(yùn)動功能梯度Timoshenko梁穩(wěn)定性分析

趙鳳群， 王忠民， 路小平

(1.西安理工大學(xué) 理學(xué)院，西安 710054；2.西安理工大學(xué) 土木建筑工程學(xué)院,西安 710054)

軸向運(yùn)動體系振動在軍事、航空航天及機(jī)械、電子工程等領(lǐng)域廣泛應(yīng)用。研究表明速度較小的軸向運(yùn)動亦足以影響系統(tǒng)動力特性。超臨界速度時(shí)，系統(tǒng)會出現(xiàn)劇烈振動、結(jié)構(gòu)不穩(wěn)定，甚至被破壞。因此，研究軸向運(yùn)動體系動力特性及穩(wěn)定性對結(jié)構(gòu)分析、設(shè)計(jì)非常重要。Euler-Bernoulli梁模型為一簡化有效計(jì)算模型，一維軸向運(yùn)動梁模型大量采用該模型[1-4]。陳立群等[5-7]對此也做過許多研究。對Timoshenko模型軸向運(yùn)動梁研究較少。Lee等[8]用譜分析方法研究均勻張力作用下軸向運(yùn)動Timoshenko梁的橫向振動特性。Tang等[9]用復(fù)模態(tài)方法研究軸向運(yùn)動Timoshenko梁振動問題，分析梁在不同邊界條件下的自振頻率、模態(tài)及臨界速度。功能梯度材料(Functionally Graded Material, FGM)為材料科學(xué)領(lǐng)域提出的新概念。此非均勻復(fù)合材料的組織、顯微結(jié)構(gòu)及性能由一側(cè)至另一側(cè)連續(xù)變化，因而較一般復(fù)合材料性能優(yōu)越，在航空航天、生物醫(yī)學(xué)、核工業(yè)等領(lǐng)域應(yīng)用前景廣闊。因此對該材料結(jié)構(gòu)研究已成熱點(diǎn)之一。Li等[10]用解析方法研究過功能梯度Timoshenko梁及Euler-Bernoulli梁的靜、動力穩(wěn)定性。而對軸向運(yùn)動FGM梁的研究報(bào)道較少。

本文基于Timoshenko梁模型，由Hamilton原理建立軸向運(yùn)動FGM Timoshenko梁運(yùn)動微分方程組，通過引入新未知函數(shù)，將該方程組化成單個(gè)方程的偏微分方程，方便后續(xù)分析。采用WDQ法，獲得簡支FGM梁的復(fù)頻率，分析軸向運(yùn)動FGM Timoshenko梁的失穩(wěn)形式、臨界速度及梯度指標(biāo)、長高比的變化對其振動特性影響。

1 控制微分方程建立

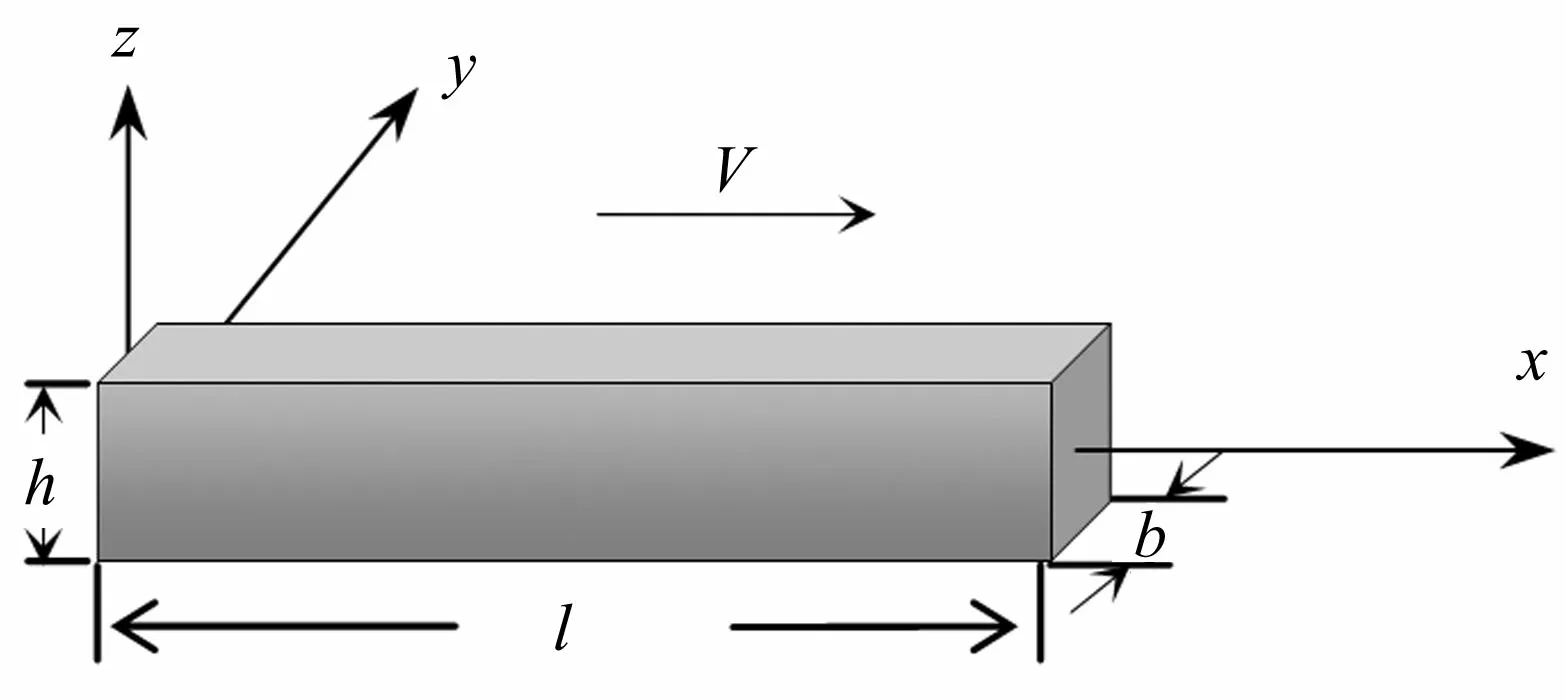
圖1 FGM Timoshenko梁及坐標(biāo)系

設(shè)FGM由陶瓷、金屬材料復(fù)合而成。圖1為矩形截面梁，長l，厚度h，寬度b，x為水平方向，z為厚度方向，V為軸向運(yùn)動速度，F(xiàn)GM的等效物性參數(shù)[11]可表示為：

(1)

其中：Xc，Xm分別為陶瓷、金屬材料物性參數(shù)；p為FGM梯度指標(biāo)。

設(shè)梁內(nèi)任一點(diǎn)在y方向位移為零，x,z方向位移u,w分別為：

(2)

式中：u0,w0為軸向、橫向位移；φ(x,t)為梁橫截面關(guān)于y軸轉(zhuǎn)角。梁內(nèi)任意點(diǎn)應(yīng)變?yōu)椋?/p>

(3)

應(yīng)力應(yīng)變關(guān)系為：

(4)

梁截面內(nèi)力分量為：

(5)

將式(3)、(4)代入式(5)，得：

(6)

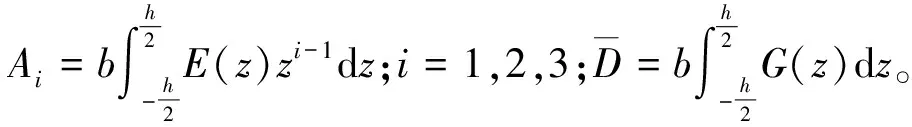
梁總動能為：

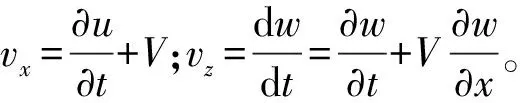
梁總動能變分為：

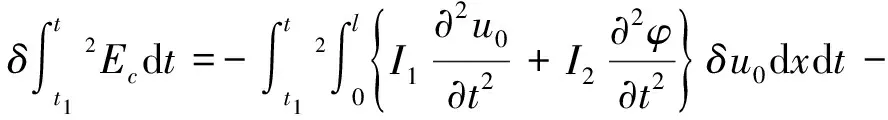
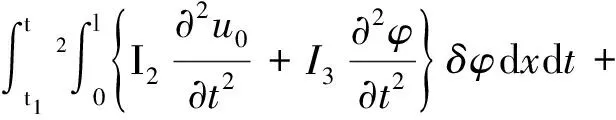
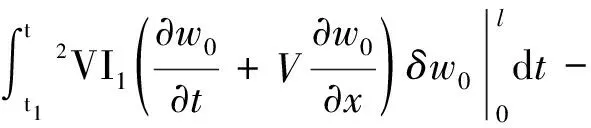
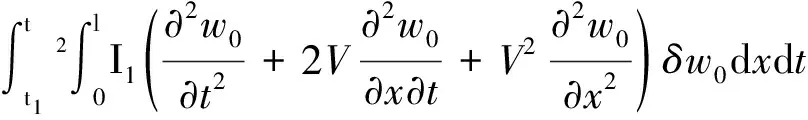
(7)

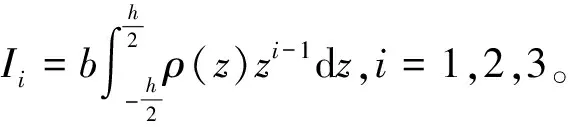
梁總應(yīng)變能變分為：

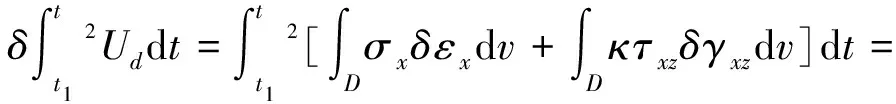
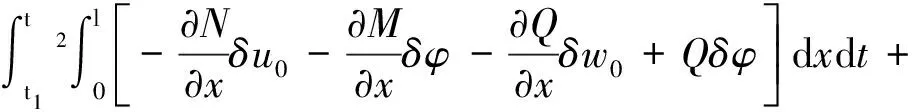
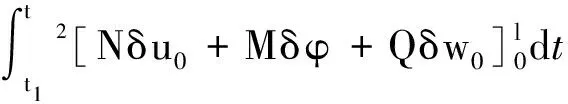
(8)

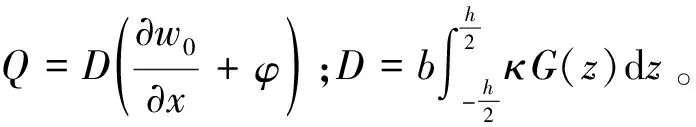
由Hamilton原理，有：

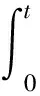
(9)

將式(7)、(8)代入式(9)，得系統(tǒng)運(yùn)動微分方程為：

(10)

邊界條件為：

(11)

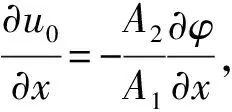
(12)

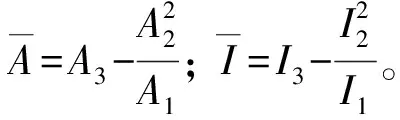
式(12)為關(guān)于w0，φ的耦合方程，較復(fù)雜，為此引入新未知函數(shù)，將式(12)轉(zhuǎn)化成只含一個(gè)未知函數(shù)的偏微分方程。設(shè)：

(13)

將式(13)代入式(12)第二式，有：

取：

(14)

將式(14)代入式(12)第一式，得用函數(shù)F表示的軸向運(yùn)動FGM Timoshenko梁運(yùn)動微分方程：

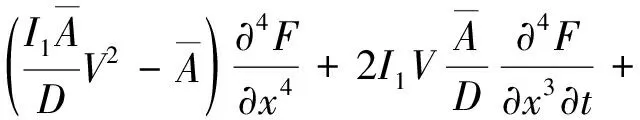
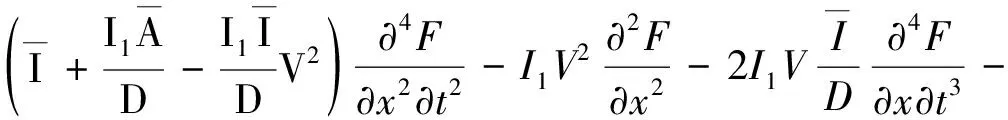
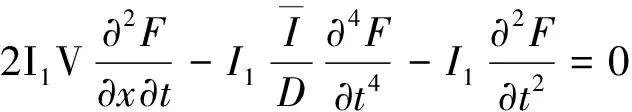
(15)

2 穩(wěn)定性分析

設(shè)F(x,t)=f(x)eiωt，代入式(15)得：

(16)

令：

得式(16)的無量綱形式：

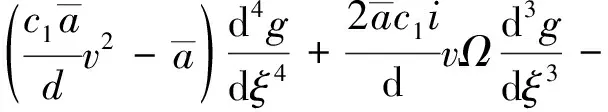
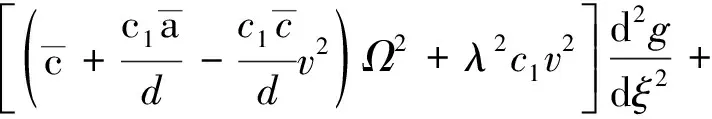
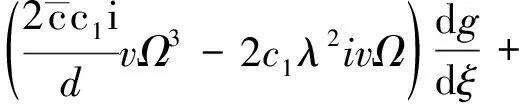
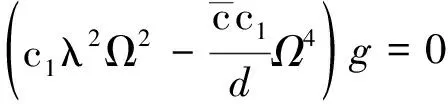
(17)

其中：

兩端簡支梁邊界條件為：

w0(0,t)=w0(l,t)=0;M(0,t)=M(l,t)=0

由此得式(17)滿足的邊界條件為：

ξ=0, 1∶g=g″=0

(18)

WDQ法為有效的數(shù)值方法，祥見文獻(xiàn)[12-13]，此處采用WDQ法求解式(17)、(18)。

設(shè)式(17)的解為：

(19)

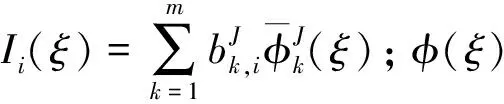
(20)

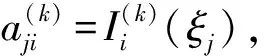
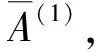
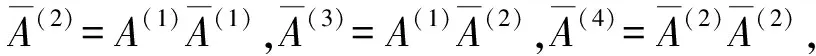
(21)

式(21)中已全部包含邊界條件式(18)。將式(21)代入式(17)，則有：

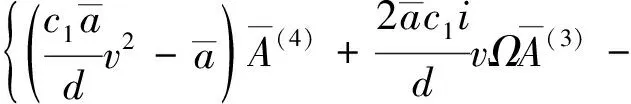
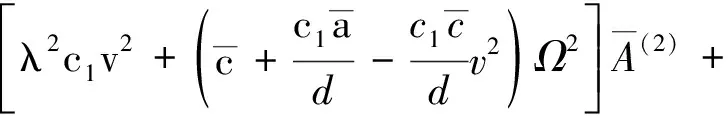
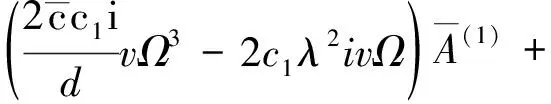
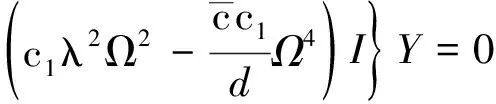
(22)

故式(17)、(18)的特征方程為：

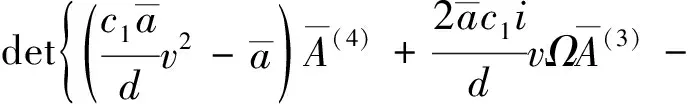
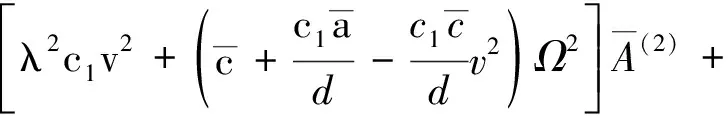
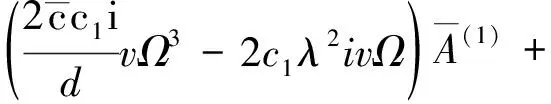
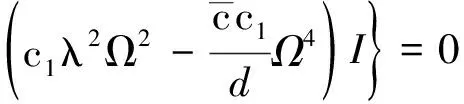
(23)

由式(23)求得復(fù)頻率Ω與運(yùn)動速度v之關(guān)系，進(jìn)而討論軸向運(yùn)動FGM Timoshenko梁動力穩(wěn)定性。

3 數(shù)值結(jié)果及分析

本研究取陶瓷ZrO2，金屬Al，參數(shù)見表1。通常泊松比ν(z)是z的函數(shù)，但變化較小，此處取常數(shù)ν=0.3。計(jì)算時(shí)取剪切修正因子κ=5/6[10]。WDQ法中小波函數(shù)φ(ξ)選Shannon函數(shù)，尺度因子取J=3，n=3。

表1 材料常數(shù)

運(yùn)動速度v=0，梯度指標(biāo)p=0時(shí)，退化成經(jīng)典Timoshenko簡支梁，文獻(xiàn)[14]中給出固有頻率精確解表達(dá)式：

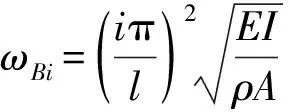
用本文方法計(jì)算所得不同長高比前三階固有頻率見表2，與文獻(xiàn)[14]結(jié)果一致，表明本文方法的有效性。

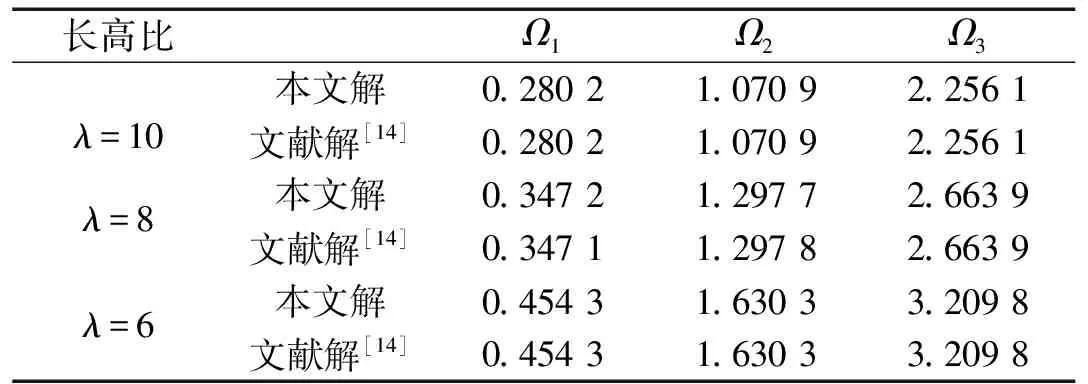
表2 Timoshenko簡支梁前三階固有頻率

3.1 軸向運(yùn)動速度對FGM Timoshenko梁穩(wěn)定性影響

p=0時(shí)，對應(yīng)于純陶瓷(ZrO2)材料梁；p→∞時(shí)，對應(yīng)于純金屬(Al)材料梁。長高比λ=10時(shí)，軸向運(yùn)動純陶瓷材料簡支Timoshenko梁前三階無量綱復(fù)頻率隨無量綱軸向運(yùn)動速度變化關(guān)系見圖2。由圖2中看出，無量綱運(yùn)動速度vvf2時(shí)，梁發(fā)生前三階模態(tài)耦合顫振失穩(wěn)，vf2為顫振失穩(wěn)臨界速度。

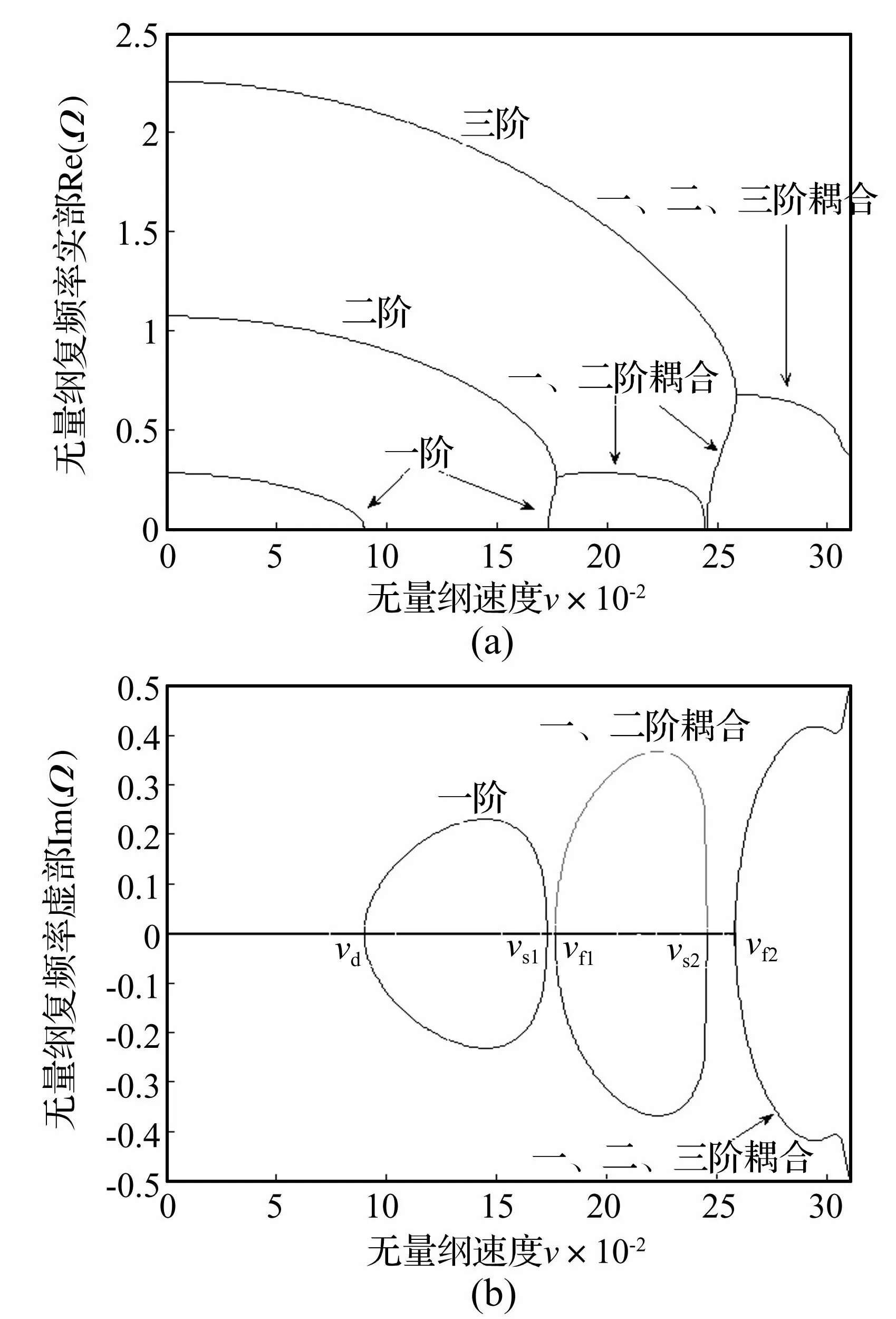
圖2 陶瓷材料Timoshenko梁前三階復(fù)頻率Ω隨速度v的變化曲線

長高比λ=10、梯度指標(biāo)p=1時(shí)，軸向運(yùn)動FGM簡支梁前三階無量綱復(fù)頻率隨無量綱軸向運(yùn)動速度變化關(guān)系見圖3。可見FGM Timoshenko梁與均質(zhì)材料Timoshenko梁振動特性、失穩(wěn)形式類似，經(jīng)歷穩(wěn)定-發(fā)散失穩(wěn)-再穩(wěn)定-耦合模態(tài)顫振-再穩(wěn)定-耦合模態(tài)顫振過程，但各階復(fù)頻率絕對值及各臨界值均變小。

為進(jìn)一步了解梯度指標(biāo)對FGM Timoshenko梁復(fù)頻率及臨界值影響，對無量綱速度v=0.05，長高比λ=10時(shí)FGM Timoshenko梁一階無量綱固有頻率Re(Ω1)隨梯度指標(biāo)p變化曲線(v=0.05時(shí)梁均處于穩(wěn)定狀態(tài))見圖4。一階發(fā)散失穩(wěn)臨界速度vd隨梯度指標(biāo)p變化曲線見圖5。由圖4、圖5看出，p約在[0,1.5]時(shí)，Re(Ω1)、vd隨梯度指標(biāo)p的增加而減小；p約在[1.5,6.5]時(shí)，Re(Ω1)、vd隨梯度指標(biāo)p的增加而增加；v>6.5時(shí)，隨梯度指標(biāo)p的增加，Re(Ω1)、vd逐漸減小并趨于金屬材料梁一階固有頻率及發(fā)散臨界速度值。其它失穩(wěn)臨界值變化過程類似，不再給出圖形。值得注意的是，當(dāng)p取某些特殊值時(shí)，對應(yīng)的FGM Timoshenko梁的Re(Ω1)及vd值相同，說明對某些不同組分含量的FGM梁，振動特性與失穩(wěn)形式一致。而FGM梁的復(fù)頻率曲線均位于陶瓷、金屬材料梁之間。

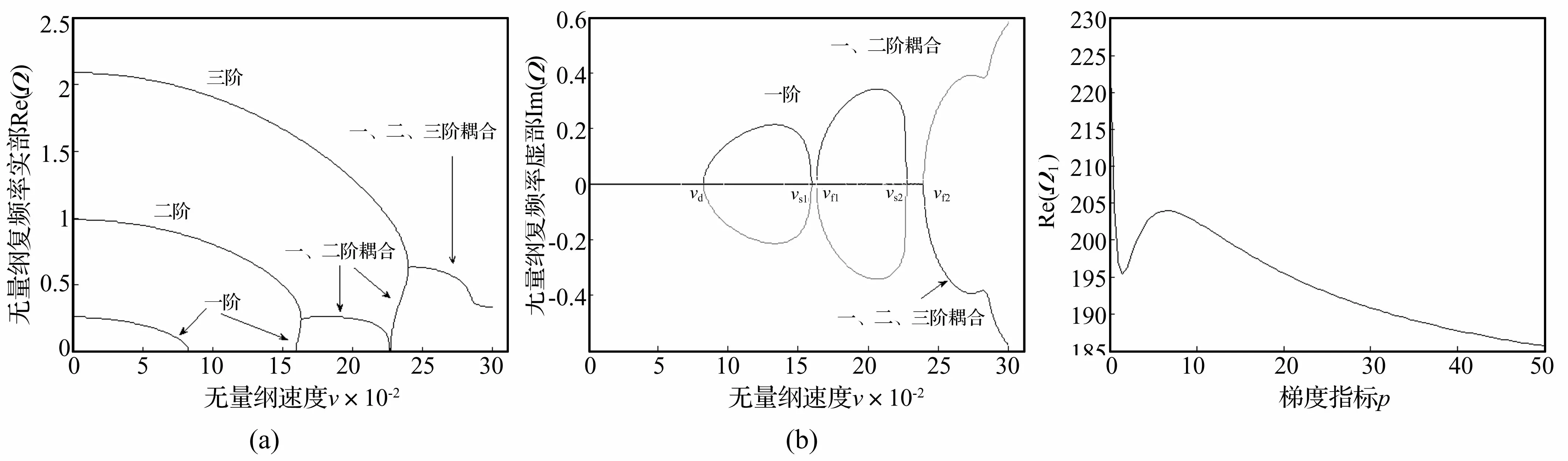
圖3 FGM Timoshenko梁前三階復(fù)頻率Ω隨速度v的變化曲線(λ=10, p=1)

圖5 一階發(fā)散臨界速度隨梯度指標(biāo)變化曲線

3.2 長高比對梁穩(wěn)定性影響

梯度指標(biāo)p=1、長高比λ=3時(shí)FGM Timoshenko梁前三階復(fù)頻率Ω隨運(yùn)動速度v變化曲線見圖6。與圖3比較看出，λ=3時(shí)FGM Timoshenko梁的穩(wěn)定性與λ=10時(shí)有所不同。圖6中0vf2時(shí)，梁在一階模態(tài)發(fā)散失穩(wěn)，二、三階模態(tài)耦合模態(tài)顫振失穩(wěn)。可見隨運(yùn)動速度的增大，λ=3的FGM Timoshenko梁經(jīng)歷穩(wěn)定-一階模態(tài)發(fā)散失穩(wěn)-一、二階耦合模態(tài)顫振失穩(wěn)-一階模態(tài)發(fā)散失穩(wěn)，二、三階模態(tài)耦合顫振失穩(wěn)過程，失穩(wěn)后不出現(xiàn)λ=10時(shí)再穩(wěn)定過程；同時(shí)， FGM Timoshenko梁的復(fù)頻率絕對值及失穩(wěn)臨界值均較λ=10時(shí)大。可見軸向運(yùn)動速度對FGM Timoshenko細(xì)長梁與粗短梁穩(wěn)定性影響不同，且隨長高比的減小，復(fù)頻率絕對值及失穩(wěn)臨界值均在增大。

4 結(jié) 論

本文通過建立軸向運(yùn)動FGM Timoshenko梁運(yùn)動微分方程，分析簡支FGM Timoshenko梁振動特性及失穩(wěn)形式，結(jié)論如下：

(1)隨運(yùn)動速度的增大，F(xiàn)GM Timoshenko細(xì)長梁會經(jīng)歷穩(wěn)定-一階發(fā)散失穩(wěn)-再穩(wěn)定-一、二階模態(tài)耦合顫振失穩(wěn)-再穩(wěn)定-前三階模態(tài)耦合顫振失穩(wěn)過程。

(2)FGM Timoshenko粗短梁失穩(wěn)形式與細(xì)長梁有所不同，且失穩(wěn)后不再出現(xiàn)穩(wěn)定狀態(tài)，其頻率、各失穩(wěn)臨界值均大于細(xì)長梁對應(yīng)值。

(3)由陶瓷、金屬材料組成FGM Timoshenko梁的復(fù)頻率介于均質(zhì)陶瓷材料Timoshenko梁與金屬材料Timoshenko梁之間。但隨梯度指標(biāo)的增加，F(xiàn)GM Timoshenko梁復(fù)頻率并非單調(diào)地從陶瓷材料梁向金屬材料梁過渡。

參 考 文 獻(xiàn)

[1]Hwang S J, Perkins N C. Supercritical stability of an axially moving beam, parts I and II[J]. Journal of Sound and Vibration, 1992,154 (3):381-409.

[2]Al-Jawi A A N, Pierre C, Ulsoy A G. Vibration localization in dual-span axially moving beams, part I: formulation and results[J]. Journal of Sound and Vibration, 1995, 179 (2):243-266.

[3]Riedel C H, Tan C A. Dynamic characteristics and mode localization of elastically constrained axially moving strings and beams[J]. Journal of Sound and Vibration,1998, 215(3): 455-473.

[4]Oz H R, Pakdemirli M. Vibrations of an axially moving beam with time-dependent velocity[J]. Journal of Sound and Vibration, 1999, 227 (2): 239-257.

[5]楊曉東, 陳立群. 變速度軸向運(yùn)動粘彈性梁的動態(tài)穩(wěn)定性[J]. 應(yīng)用數(shù)學(xué)和力學(xué), 2005, 26(8): 905-910.

YANG Xiao-dong, CHEN Li-qun. Dynamic stability of axially moving viscoelastic beams with pulsating speed[J]. Applied Mathematics and Mechanics, 2005,26(8): 905-910.

[6]Yang X D, Chen L Q. Steady-state response of axially moving viscoelastic beams on a vibrating foundation[J]. Acta Mechanica Solida Sinica, 2006, 19(4): 365-373.

[7]Chen L Q, Yang X D. Nonlinear free transverse vibration of an axially moving beam: comparison on of two models[J]. Journal of Sound and Vibration, 2007, 299(12): 348-354.

[8]Lee U, Kim J, Oh H. Spectral analysis for the transverse vibration of an axially moving Timoshenko beam[J]. Journal of Sound and Vibration, 2004, 271(3-5):685-703.

[9]Tang Y Q,Chen L Q, Yang X D. Natural frequencies, modes and critical speeds of axially moving Timoshenko beams with different boundary conditions[J]. International Journal of Mechanical Sciences,2008,50(10-11):1448- 1458.

[10]Li X F. A unified approach analyzing static and dynamic behaviors of functionally graded Timoshenko and Euler-Bernoulli beams[J]. Journal of Sound and Vibration, 2008, 318(4-5):1210-1229.

[11]Tanigawa Y, Akai T, Kawamura R,et al. Transient heat conduction and thermal stress problems of a non-homogeneous plate with temperature-dependent material properties[J]. Journal of Thermal Stresses, 1999, 19(1):77-102.

[12]趙鳳群，張培茹，張瑞平.兩點(diǎn)邊值問題的小波配點(diǎn)法[J].計(jì)算力學(xué)學(xué)報(bào),2009,26(6):947-950,955.

ZHAO Feng-qun, ZHANG Pei-ru, ZHANG Rui-ping. A wavelet collocation method for solving two-point boundary value problems[J]. Chinese Journal of Computational Mechanics，2009, 26(6): 947-950,955.

[13]趙鳳群,王忠民, 張菊梅. 基于WDQ法的粘彈性輸流管道穩(wěn)定性分析[J]. 計(jì)算力學(xué)學(xué)報(bào),2011, 28 (4): 584-589.

ZHAO Feng-qun, WANG Zhong-min, ZHANG Ju-mei. The stability of visco-elastic pipes conveying fluid based on the WDQ method[J]. Chinese Journal of Computational Mechanics, 2011, 28 (4): 584-589.

[14]Blevins R D. Formulas for natural frequency and mode[M]. New York:Van Nostrand Reinhold Company, 1979.