基于粗糙集與神經網絡集成的制造過程質量診斷技術研究

江大偉1,周 平2,李麗華2

（1.威高集團，山東威海 264300;2.濟南鑄造鍛壓機械研究所有限公司，山東濟南 250022）

0 前言

機械制造質量診斷過程中，在保證質量診斷精度大致不變的情況下，如何盡可能減少特征維數，降低計算工作量和減少不確定性因素的影響，是一個亟待解決的問題。質量問題產生的機理不甚清楚，故障的表現形式不唯一，有時甚至是含糊的，在提取故障特征時也時常帶有盲目性，從而導致了實際描述的質量問題不夠分明。診斷推理是根據特定的映射關系由故障征兆域到故障原因域的計算求解問題，神經網絡[1,2]具有強大的模式分類能力，在智能故障診斷中得到了廣泛應用。但當神經網絡規模較大、樣本較多時，會含有大量冗余信息，導致網絡學習復雜，訓練時間過長。這些對神經網絡的精度及泛化能力均會產生影響。粗糙集（RS，Rough Set）的知識約簡有利于提高前者的學習能力，并能求出各影響因素的重要程度，而神經網絡的良好抗噪性能可以很好地彌補后者的缺陷。因此，基于兩者有機結合進行制造過程質量診斷研究對提高質量診斷效率及產品質量具有重要意義。

1 粗糙集理論與方法

粗糙集[3]是波蘭科學家Pawlak Z于1982年提出的一種數據分析理論。這一理論無需任何附加信息或者先驗知識就能有效地分析和處理不精確、不完整和不一致等各種不完備數據，從中發現隱藏的知識、揭示潛在的規律。

1.1 知識表達系統

知識表達系統在智能數據處理中占有十分重要的地位。形式上，四元組 S=（U，A，V，f）是一個知識表達系統。

U：對象的非空有限集合，稱為論域；

A：屬性的非空有限集合；

f：U×A→V是一個信息函數，它為每個對象的每個屬性賦予一個信息值，即?a∈A，x∈U，f（x，a）∈Va。

知識表達系統的數據以關系表的形式表示。關系表的行對應要研究的對象，列對應對象的屬性，對象的信息是通過制定對象的各屬性來表達。

決策表是一類特殊的重要的知識表達系統。

A=C∪D，C∩D=φ，C為條件屬性集，D 為決策屬性集。具有條件屬性和決策屬性的知識表達系統稱為決策表。

1.2 屬性約簡

一般約簡算法，是一個窮盡搜索的過程，需要的時間復雜度很大，因此引入了可辨識矩陣的方法。

差別矩陣（Discernibility Matrix）也稱可辨識矩陣，它在核的計算中有重要作用，該算法是由波蘭華沙大學數學家Skowron于1992年提出的。

決策表S=f（U，R，V，f）（R=C∪D）的差別矩陣是一個對稱的U×U矩陣，矩陣的每一項Cij表示為：

2 基于粗糙集—神經網絡結合的工序質量診斷模型

為解決神經網絡規模擴大、樣本數量多過程中造成的產生學習復雜、訓練時間長問題，利用粗糙集的約簡來提高神經網絡的學習能力，提高質量診斷效率和正確率。

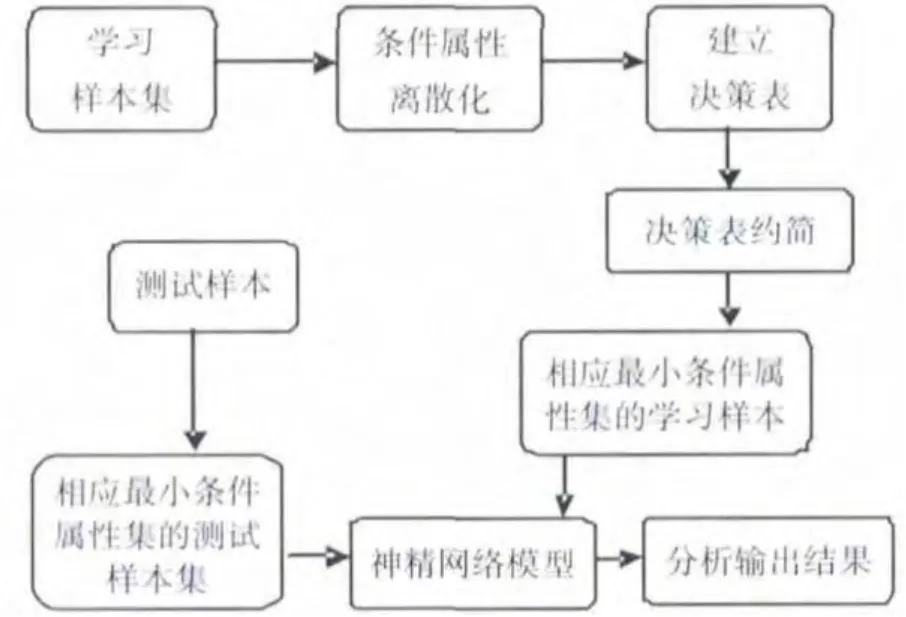
圖1 基于粗糙集-神經網絡結合的工序質量診斷流程示意圖

2.1 粗糙集數據預處理

離散化處理。粗糙集方法是一類符號化分析方法，所有的屬性值均看作定性數據。若定量數據要和定性數據綜合處理，則需將定量數據轉換成定性數據。離散化處理方法很多，如等間隔劃分法、等頻率間隔劃分法、基于條件信息墑的方法、L-方法、W-方法、P-方法和C-方法等。本文采用自組織神經網絡方法，該網絡模擬大腦神經系統自組織特征映射的功能。它是一種競爭型網絡，采用無監督學習算法進行網絡訓練，此網絡廣泛應用于樣本分類、排序和樣本檢測等方面。

2.2 建立決策表和屬性約簡

由離散化后的數據組成決策表，條件屬性(離散化后的參數)和決策屬性(參數所對應的故障類別)知識約簡先刪除決策表中冗余的行，然后利用分辨矩陣進行屬性約簡。

2.3 建立神經網絡模型

前饋式神經網絡是眾多神經網絡模型中應用最為廣泛的網絡之一，具有較強的模式分類能力。誤差反向傳播神經網絡（BP網絡[4]）具有很強的生物背景，具有多輸入多輸出特性。建立神經網絡模型的具體步驟為：首先將約簡整理后的數據決策表作為神經網絡的訓練樣本進行訓練，并對故障類別進行編碼作為網絡的輸出，獲得各自的連接權值和閾值；然后存儲相應的連接權值，形成知識庫；最后用訓練好的網絡進行質量診斷[5]。本文采用最常用的3層網絡結構的BP（Back Propagation）網絡模型，該神經網絡模型的學習算法采用Levenberg-Marquardt（批處理）的BP算法。

3 案例分析

以某機床廠高硬度軸（材料為42CrMo，淬火）磨削為例，說明基于粗糙集理論與BP神經網絡集成質量診斷方法在該磨削工序中的應用，尋求影響表面粗糙度的因素，并且分析主因和次因，即求出各影響因素對粗糙度的影響程度大小。

該磨削工序為加工一批機床零件，該生產工序的質量決策表如表1所示。表中屬性值是已經離散化處理的數值。

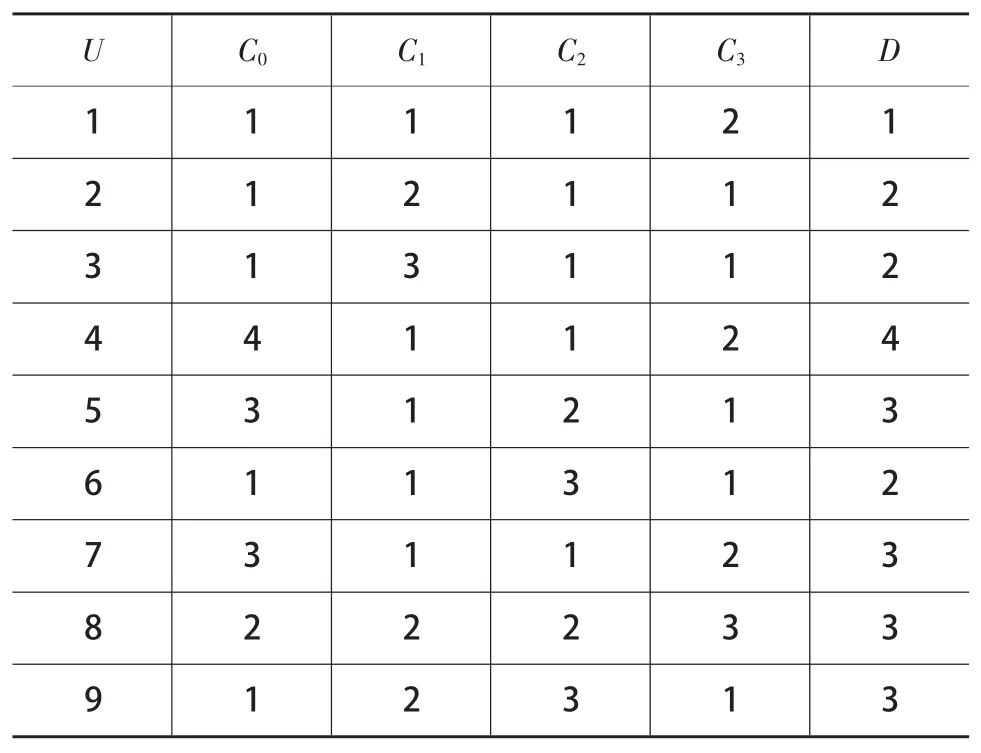
表1 42CrMo軸粗糙度原始決策表（完備）

由上述可區分矩陣可以看到有三個單元素，即該決策表的三個核，并且約簡結果也是{C0,C1,C2}。

分別計算每個條件屬性對決策屬性的影響：

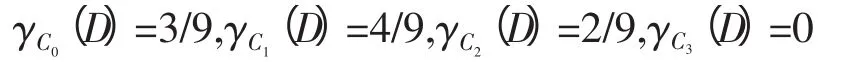
結果分析：最重要影響因素是工件轉速，其次為分形維、進給量。所以在控制粗糙度時，重點控制工件轉速、分形維和進給量就能保證加工產品的質量，提高質量診斷效率，降低診斷成本。

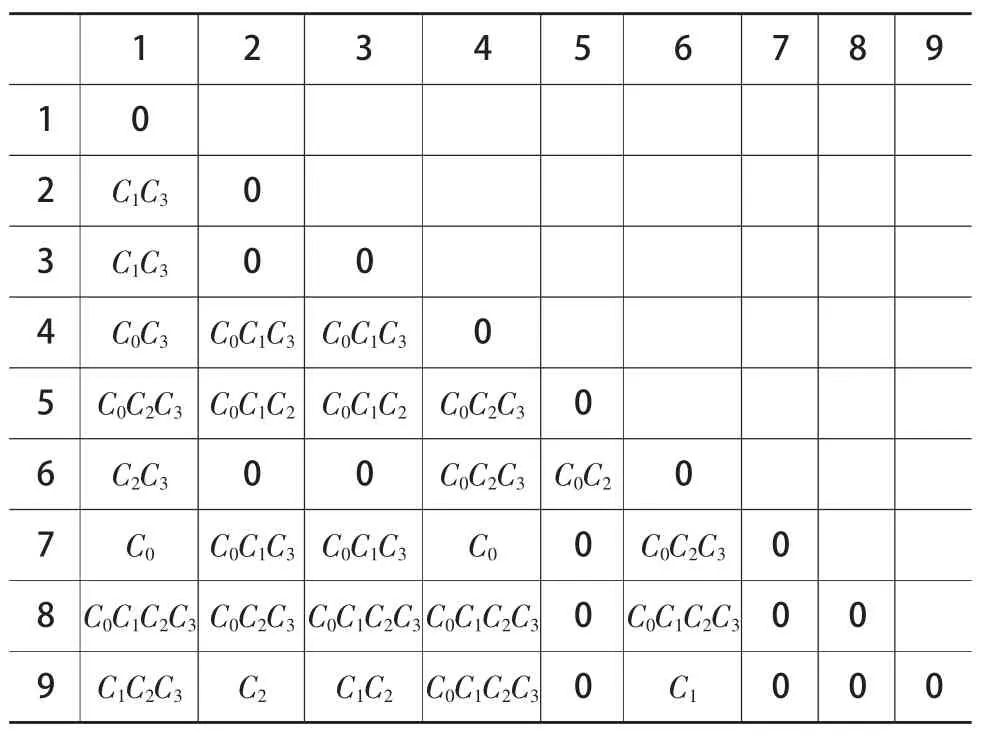
表2 軸粗糙度可區分矩陣

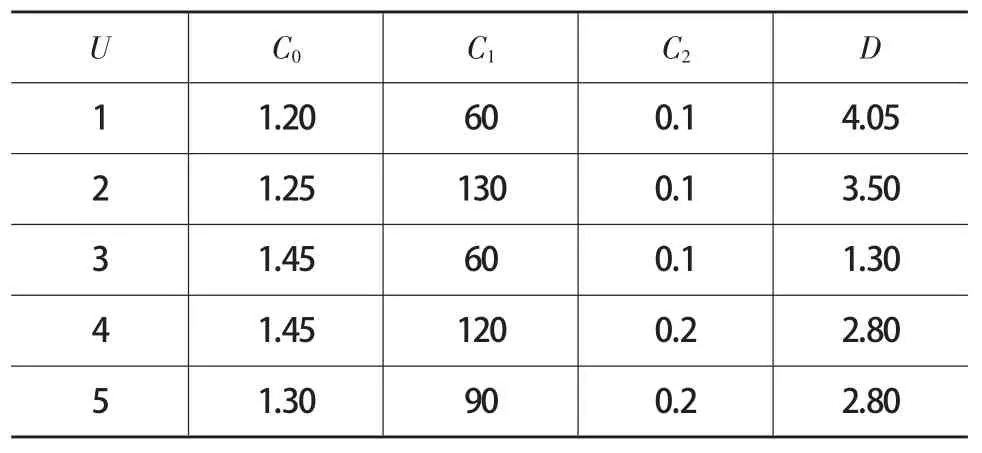
表3 待測試樣本

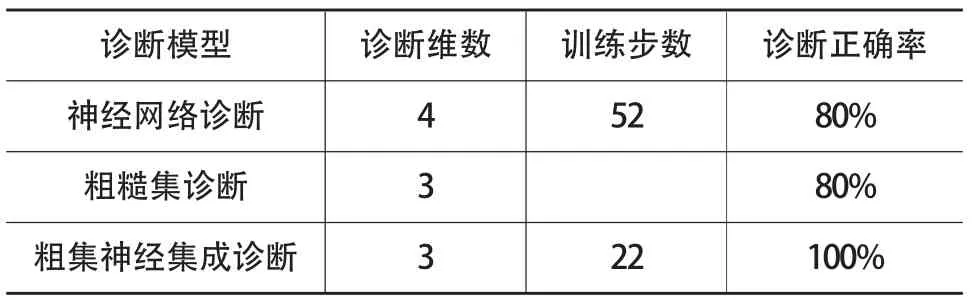
表4 實驗結果

從上表可看出神經網絡學習步數縮短，單純的神經網絡和單純的粗糙集診斷模型的準確率要比其集成低，原因在于神經網絡在冗余屬性多時會產生過配合的現象，粗糙集在于抗噪性差以及泛化能力差，導致診斷錯誤。兩者集成使神經網絡的訓練步數縮短，且診斷正確率提高，是由于影響因素屬性減少，因此大大提高了診斷效率。

4 總結

通過實驗證明,基于粗糙集與神經網絡質量診斷模型在制造過程質量診斷方面具有很好的適用性和可行性，該方法可以充分發揮各自的優勢，粗糙集理論對知識進行約簡,利用最終決策表建立的BP神經網絡具有更好的拓撲結構，其學習速度、判斷能力及容錯能力都有很大的提高。實例診斷結果表明：利用此方法可大大提高診斷效率，降低診斷成本，可為解決現代工業工程中的質量診斷提供有效的參考。

[1]朱凱,王正林.精通MATLAB神經網絡[M].北京:電子工業出版社,2010.

[2]張騰飛,王錫淮,葉銀忠,肖健梅.粗糙集理論在故障診斷中的應用綜述[J].上海海事大學學報,2005,26（4）:20-24.

[3]張文修,吳偉志,梁吉業,李德玉.粗糙集理論與方法[M].北京:科學出版社,2008.

[4]李增亮,王慶楠,李成平.BP網絡在液壓驅動螺桿泵故障診斷中的應用[J].石油機械，2006，34（8）48-50.

[5]楊占璽,韓秋實.基于信息融合技術的加工過程監測系統研究[J].機械設計與制造,2009,9（8）,243-244.