旋轉式平臺慣導系統隨機誤差自補償技術研究

楊建業，范小虎，趙旭陽，汪立新(.第二炮兵工程大學士官學院，山東青州6500;.第二炮兵工程大學自動控制工程系，西安7005)

旋轉式平臺慣導系統隨機誤差自補償技術研究

楊建業1*，范小虎1，趙旭陽1，汪立新2
(1.第二炮兵工程大學士官學院，山東青州262500;2.第二炮兵工程大學自動控制工程系，西安710025)

針對旋轉式平臺慣導中旋轉運動對慣性儀表的隨機誤差是否有抑制的問題，在建立旋轉式平臺慣導系統誤差傳播方程的基礎上，利用積分換元法建立了臺體旋轉前后系統導航誤差與噪聲相關函數間的數學表達式，討論了旋轉運動對白噪聲和3種典型有色噪聲的抑制情況。得出了旋轉運動對白噪聲無抑制、在旋轉速率滿足一定條件時對典型有色噪聲有抑制的結論。最后通過仿真驗證了理論分析的正確性。研究結果為旋轉式平臺慣導系統的工程設計、改進提供一定的理論支持。

旋轉;平臺慣導系統;隨機誤差;自補償

將旋轉平均技術應用于平臺慣導系統可以有效抑制慣性儀表常值誤差，提高平臺慣導系統的自主導航精度。在國外將采用了旋轉平均技術的此類平臺系統稱為Carouseling Gimbaled Inertial Navigation System［1］，文中將此譯為旋轉式平臺慣導系統。國外對旋轉式平臺慣導系統的研究已經非常成熟，且在美、俄等國的海軍艦艇、飛機上已得到成功應用［2-6］。目前國內許多單位已經對旋轉平均技術在慣導系統上的應用進行了深入的研究，相關單位已有原理樣機面世。但國內文獻對旋轉式慣導系統的研究主要集中在常值誤差的自補償機理和初始對準方面［7-8］，而對隨機誤差的自補償機理研究相對較少。本文將對旋轉式平臺慣導系統隨機誤差的傳播特性進行研究，探討平臺臺體的旋轉運動對白噪聲和典型有色噪聲的抑制情況。

1 旋轉式平臺慣導誤差傳播方程

參照文獻［9-10］分別定義坐標系:i為地心慣性坐標系、e為地球坐標系、g為地理坐標系、N為導航坐標系、T為理想平臺坐標系、P為實際平臺坐標系、c為計算坐標系。

與普通平臺慣導系統不同，在旋轉式平臺慣導系統中引入了一個新坐標系——“虛擬平臺坐標系P'”，將其定義為臺體未加調制指令時的實際平臺系，理想情況下該坐標系應當與T系重合。將P'系相對T系的誤差角定義為旋轉式平臺慣導系統的姿態誤差角。在普通平臺慣導系統中，P'系與P系重合，姿態誤差角的定義退化為P系相對T系的誤差角，與平臺慣導系統中姿態誤差角的定義相一致。在文獻［11-13］的基礎上建立旋轉式平臺慣導系統的誤差傳播方程，如下所示。

速度誤差傳播方程:

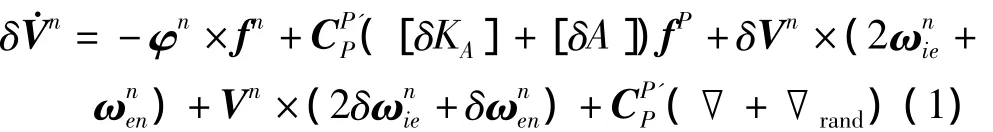
姿態誤差傳播方程:

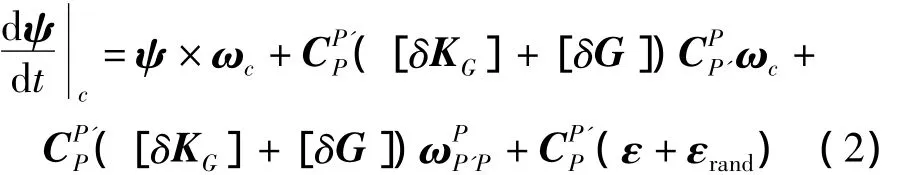
其中，▽與ε分別為加速度計和陀螺儀的常值誤差，▽rand與εrand分別為加速度計和陀螺儀的隨機誤差。對常值項、安裝誤差、標度因數誤差的抑制情況筆者已在相關文獻中進行了討論，本文將研究旋轉對隨機誤差的抑制情況，將以旋轉對加速度計隨機誤差的抑制為例來研究旋轉式平臺慣導系統隨機誤差的傳播特性。由式(1)可得，旋轉前加速度計隨機誤差引起的導航誤差項為▽rand，旋轉后變為CP'P▽rand。

設坐標OXNYNZN相對慣性空間不動，OXPYPZP相對OXNYNZN繞OZN軸旋轉，載體在XOY確定的平面內運動，則臺體不旋轉時加速度計隨機誤差引起的速度誤差為:

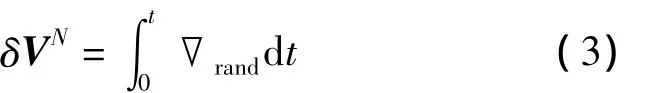
臺體旋轉時速度誤差變為:

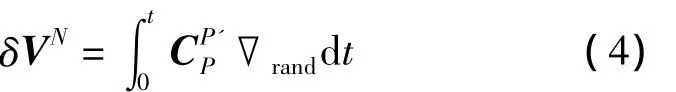
其中

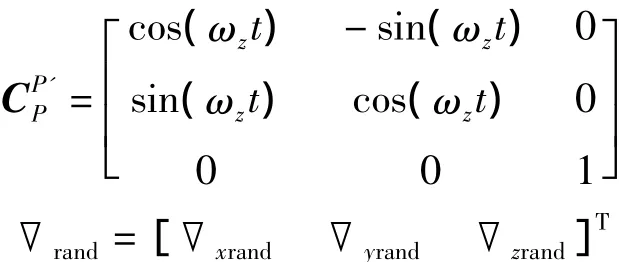
為了分析方便，假設▽yrand=▽zrand=0，只討論在隨機誤差▽xrand激勵下，旋轉前后δVN方差的變化情況。

2 導航誤差方差與噪聲相關函數間的關系

2.1 積分換元法

設f(x，y)在xOy平面上的閉區域D上連續，變換

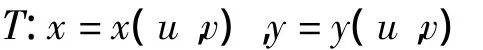
將uOv平面上的閉區域D'變為xOy平面上的D，且滿足:

①x(u，v)，y(u，v)在D'上具有一階連續偏導數;

②在D'上雅可比式

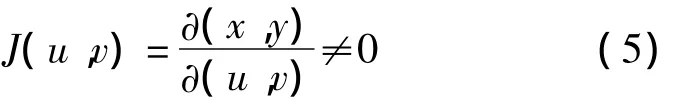
③變換T:D'→D是一對一的，則有:

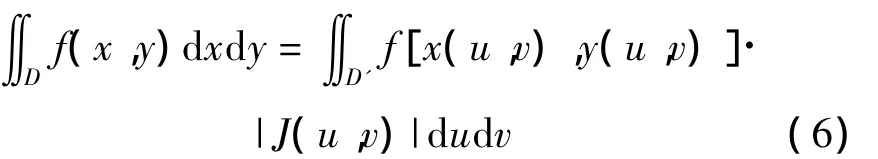
2.2 導航誤差方差與噪聲相關函數間的關系

設▽rand=［▽xrand0 0］T，▽xrand為平穩隨機過程，其自相關函數為:

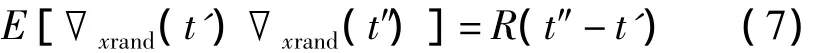
則δVx(t)、δVy(t)及δVz(t)均為隨機過程，當臺體未旋轉時，其自相關函數為:

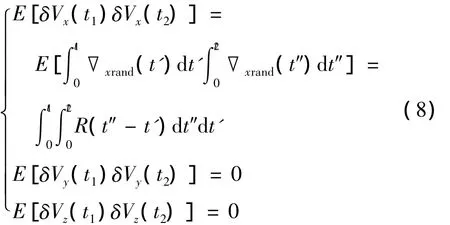
對式(8)的積分變量進行下列變換:

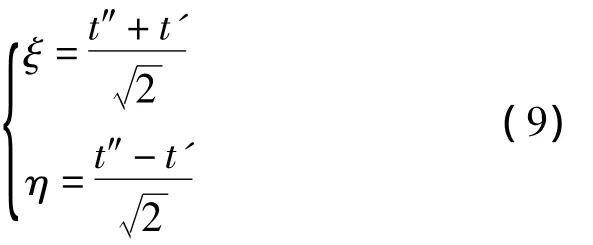
在t1=t2=t 的條件下，利用換元定理進行換元，變換前后積分區域如圖1所示。

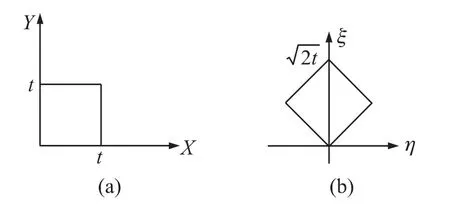
圖1 變換前后的積分區域

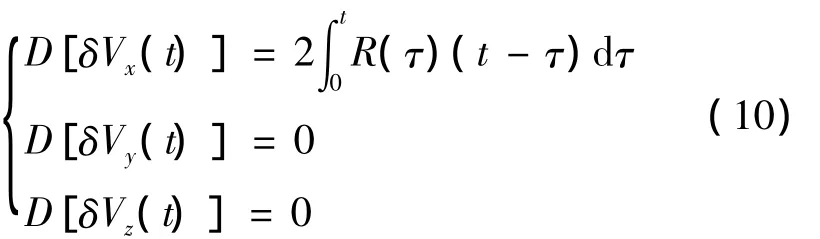
其合速度誤差的方差為:

當臺體旋轉時，速度誤差的自相關函數為:

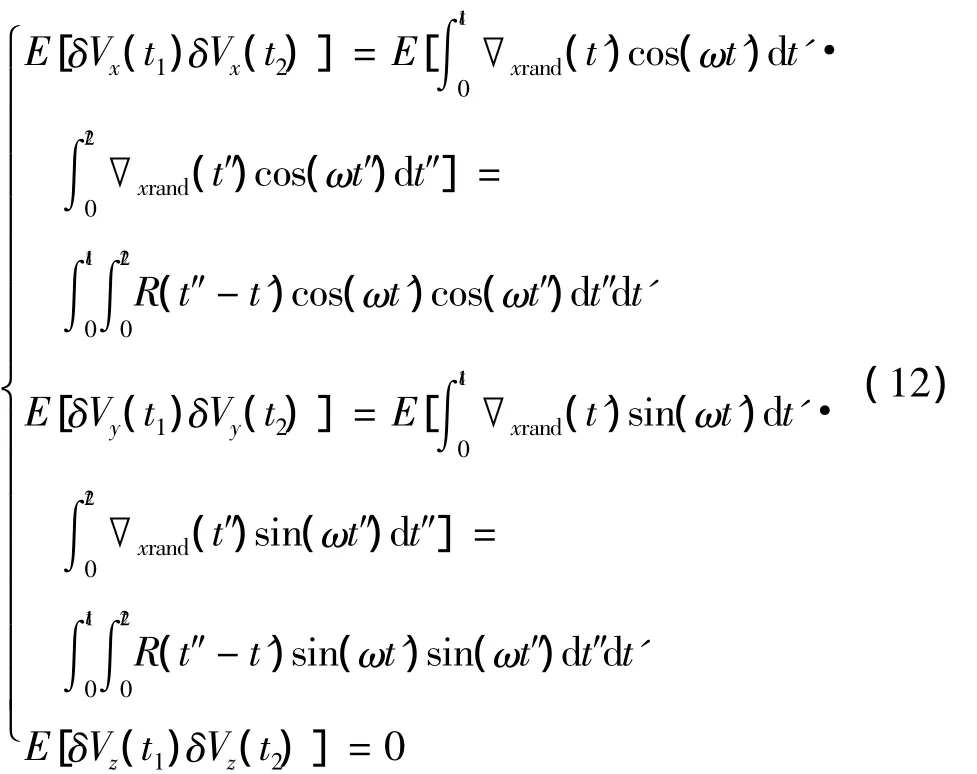
在t1=t2=t的條件下，將變量η變換為τ=，進行積分換元后得:

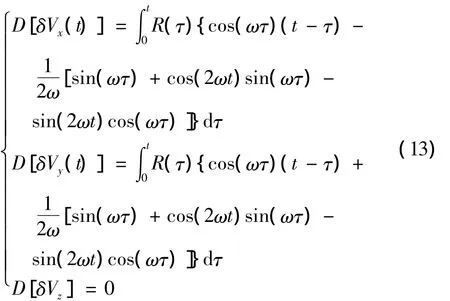
臺體旋轉時合速度誤差為

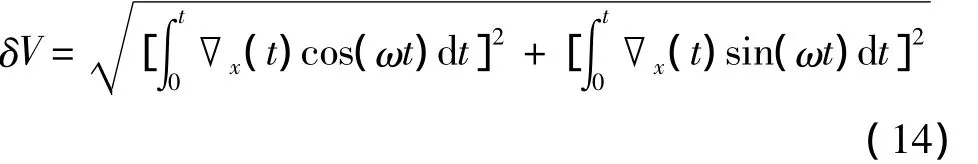
則其自相關函數為:

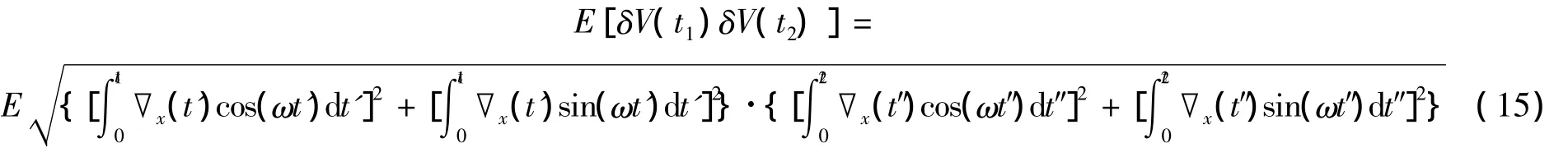
當t=t1=t2時，由式(13)和式(15)可得，臺體旋轉時合速度誤差方差為:

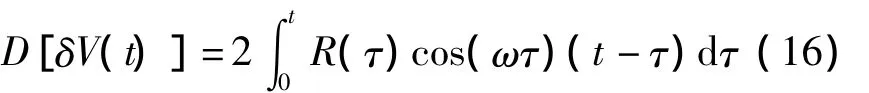
2.3 旋轉運動對白噪聲抑制分析

設白噪聲的自相關函數R(τ)=Nδ(τ)，δ(·)為δ函數，當臺體未旋轉時

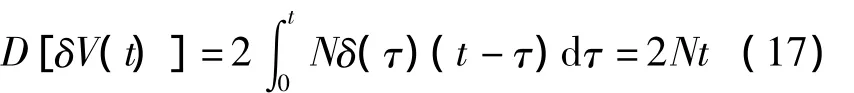
當臺體旋轉時

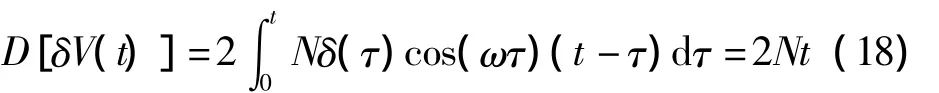
由式(17)和式(18)得，臺體旋轉前后速度誤差的方差表達式相同，即旋轉對白噪聲沒有抑制作用。

2.4 旋轉運動對典型有色噪聲抑制分析

本小節將研究旋轉對3種典型有色噪聲的抑制情況，3種有色噪聲的自相關函數分別為:

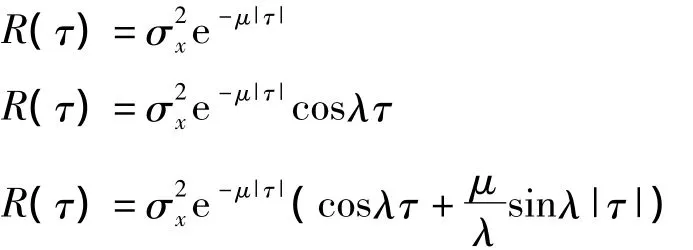
當臺體不旋轉時，將噪聲自相關函數的表達式代入式(11)得:

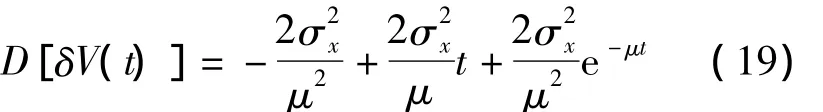
當臺體旋轉時，將噪聲自相關函數的表達式代入式(16)得:

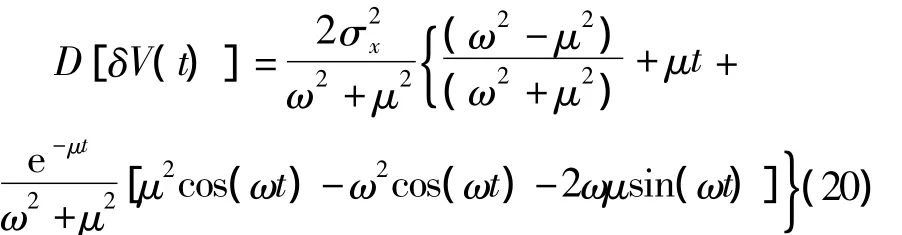
由式(19)和式(20)可以看出，速度誤差的方差由常值項、隨時間增長項和周期項三部分組成，其中對方差貢獻較大的是隨時間增長的項。

當臺體不旋轉時，速度誤差的方差表達式為:

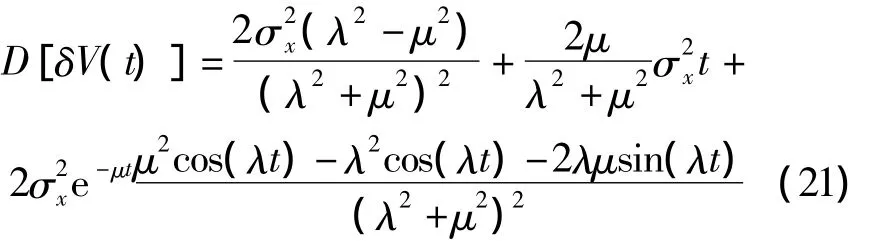
當臺體旋轉時，速度誤差的方差表達式為:

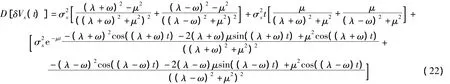
當臺體不旋轉時，速度誤差的方差表達式為:

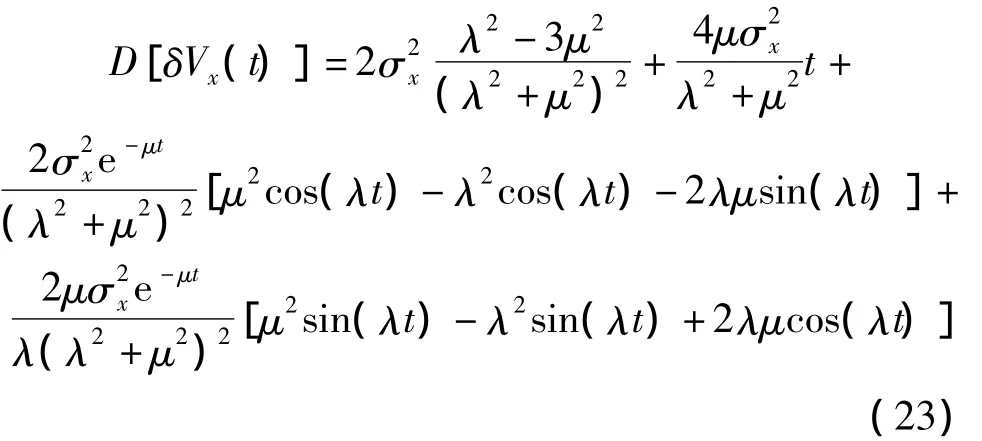
臺體旋轉時，速度誤差的方差表達式變為:

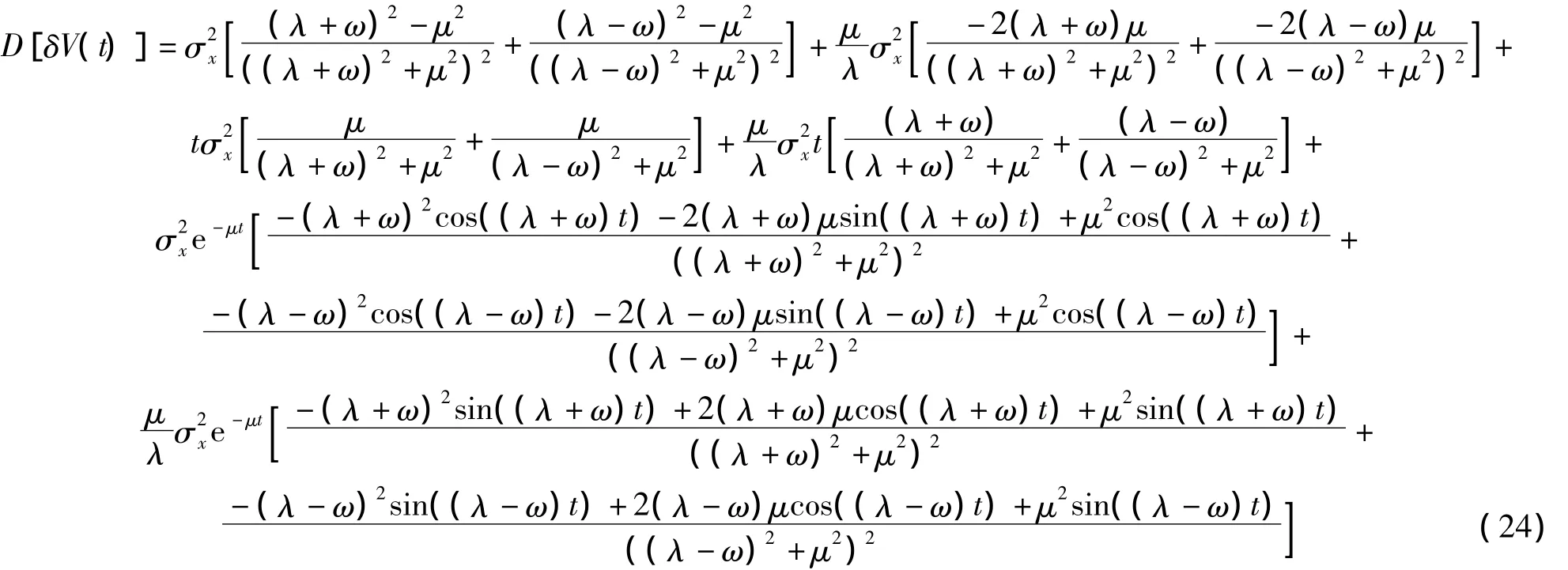
3 仿真及結果分析

3.1 仿真

(1)對有色噪聲一的抑制

取σx=0.01，μ=0.01，圖2示出旋轉前后速度誤差方差的對比關系(ω=3(°)/s)，圖3為隨時間增長項系數與旋轉速度ω的函數關系。

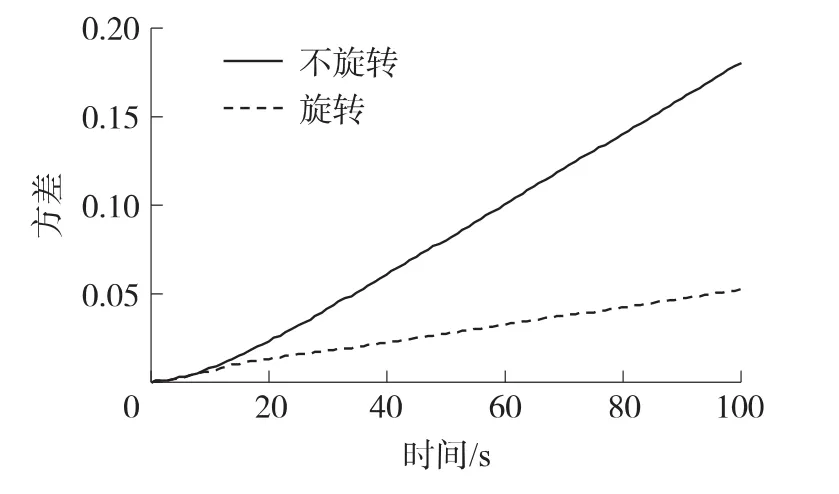
圖2 速度誤差方差與時間的關系(R(τ)=σ2x e-μ|τ|)

(2)對有色噪聲二的抑制

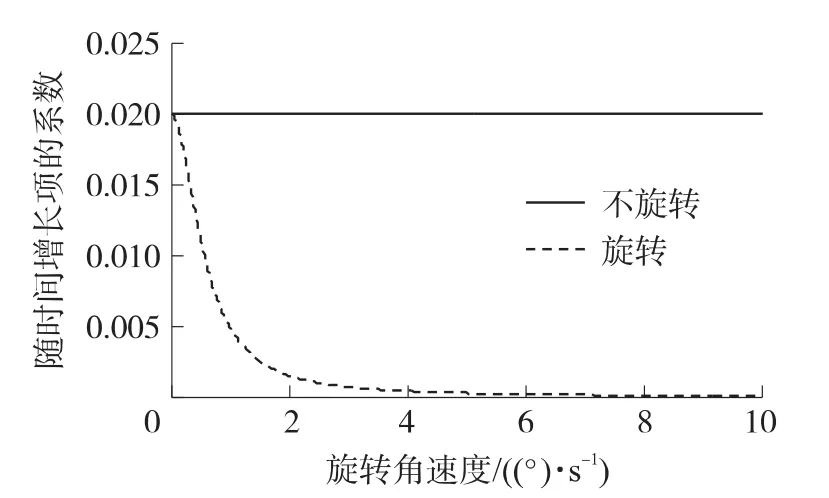
圖3 隨時間增長項的系數與旋轉速率間關系(R(τ)=σ2x e-μ|τ|)

取σx=0.01，λ=μ=0.01，圖4示出旋轉前后速度誤差方差的對比關系(ω=3(°)/s)，圖5為隨時間增長項的系數與旋轉速度ω的函數關系。

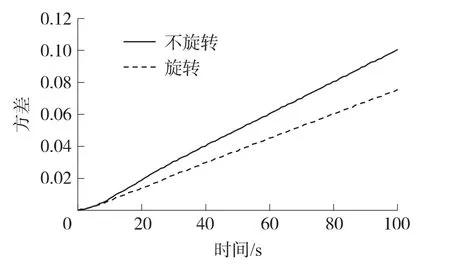
圖4 速度誤差方差與時間的關系(R(τ)=σ2x e-μ|τ|cosλτ)

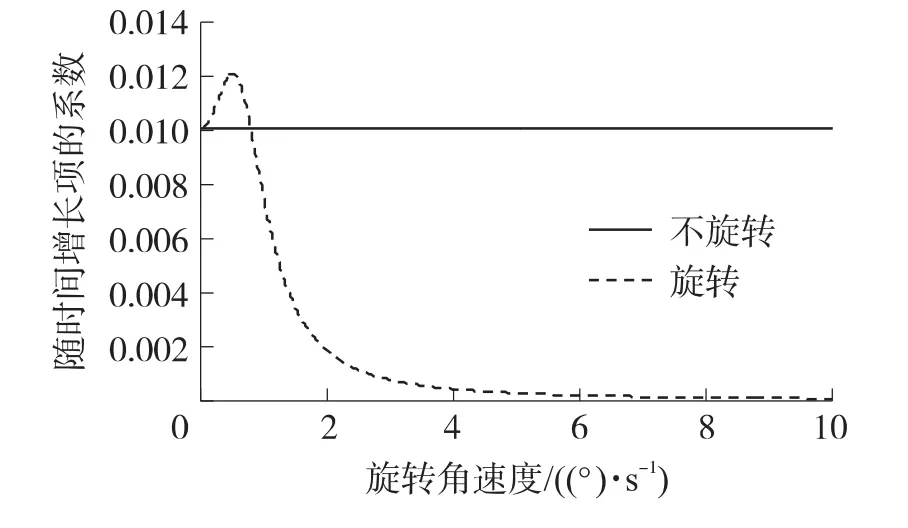
圖5 隨時間增長項的系數與調制速率間關系(R(τ)=σ2x e-μ|τ|cosλτ)

(3)對有色噪聲三的抑制

取σx=0.01，λ=μ=0.01，圖6示出旋轉前后速度誤差方差的對比關系(ω=3(°)/s)，圖7為隨時間增長項的系數與旋轉速度的函數關系。

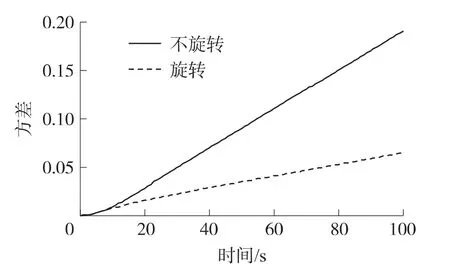
圖6 速度誤差方差與時間的關系

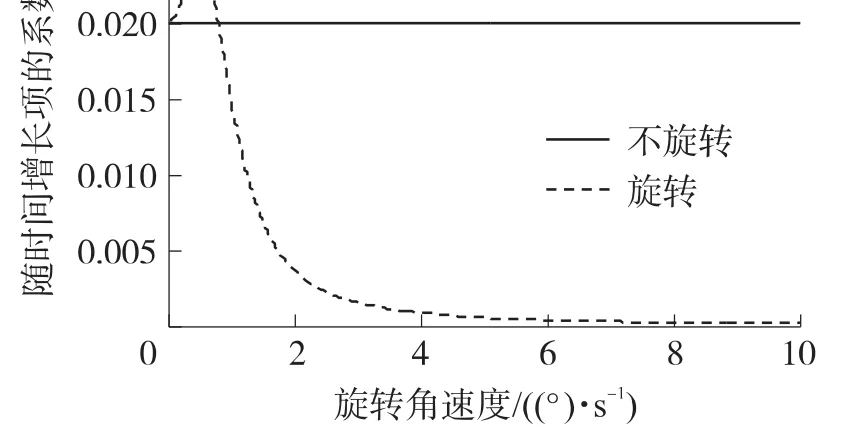
圖7 隨時間增長項的系數與調制速率間關系

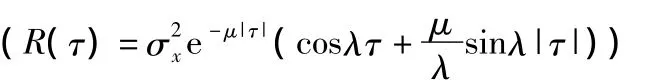
3.2 結果分析

由圖2、圖4及圖6可得出，在臺體以ω= 3(°)/s旋轉時，速度誤差的方差變小，即在此種情況下旋轉對文中的3種典型有色噪聲均有抑制作用;由圖3、圖5及圖7可得出，當旋轉角速度ω滿足一定條件時，隨著ω的增大，隨時間增長項的系數會極大減小，即提高旋轉角速度可以增加對文中典型有色噪聲的抑制效果。

綜上所述，旋轉對白噪聲沒有抑制作用，當調制速度ω滿足一定條件時對文中的典型有色噪聲有抑制作用。

4 結論

本文對旋轉式平臺慣導系統的隨機誤差傳播特性進行了研究。推導了旋轉前后各種噪聲引起的導航誤差方差與噪聲自相關函數的關系式，討論了旋轉對白噪聲及3種典型有色噪聲的抑制情況。最后得出結論:對白噪聲沒有抑制，在一定條件下對文中所討論的3種典型有色噪聲有抑制作用。本文的研究成果為旋轉式平臺慣導系統的工程設計、改進提供了一定的理論支持。

［1］Mohinder S G，Lawrence R W，Angus P A.Global Positioning Systems，Inertial Navigation，and Integration［M］.2nd Ed.Wiley-Interscience:A John Wiley and Sons，Inc.，Publication，2007:26-27.

［2］Sciegienny J，Nurse R，Wexler J，et al.Inertial Navigation System Standardized Software Development Final Technical Report VolumeⅡofⅣINS Survey and Analytical Development［R］.The Charles Stark Draper Laboratory，Inc.，Massachusetts，USA.1976.

［3］王榮穎，許江寧，卞鴻巍，等.方位旋轉式平臺慣導系統的誤差分析與仿真［J］.系統仿真學報，2009，21(15):4786-4789.

［4］Hays K M，Schmidt R G，Campbell J D，etal.A Submarine Navigator for the 21st Century［J］.IEEE，2002(4):179-188.

［5］Levinson D E，Horst J T，Willcocks M.The Next Generation Marine Inertial Navigator Is Here Now［J］.IEEE，1994(2):121-127.

［6］Lahham J I，Brazell J R.Acoustic Noise Reduction in the MK49 Ship’s Inertial Navigation System［J］.IEEE，1992(3):32-39.

［7］于旭東，龍興武，王宇，等.激光陀螺單軸旋轉慣導系統多位置對準技術研究［J］.傳感技術學報，2011，24(6):824-828.

［8］于旭東，王宇，張鵬飛，等.單軸旋轉慣導系統在晃動基座上的建模及誤差分析［J］.傳感技術學報，2009，22(2):289-292.

［9］秦永元.慣性導航［M］.北京:科學出版社，2007.

［10］謝列托維其C M.陀螺系統儀表誤差的自動補償［M］.趙榮先，雷傳琪，謝和持，譯.北京:國防工業出版社，1986.

［11］Savage P G.Strapdown Analytics［M］.Strapdown Associate，Inc.，Maple Plain，Minnesota.2000.

［12］Savage P G.Strapdown Inertial Navigation Integration Algorithm Design Part1:Attitude Glgorithms［J］.Journal of Guidance，Control and Dynamics，1998，21(1):19-28.

［13］Savage P G.Strapdown Inertial Navigation Integration Algorithm Design Part 2:Velocity and Position Algorithms［J］.Journal of Guidance，Control and Dynamics，1998，21(2):208-229.

楊建業(1983-)，男，青海樂都人，博士，講師，主要從事慣性系統及其標定測試、新型慣導系統等方面的教學和科研工作，yangjianye2002@126.com;

汪立新(1966-)，男，湖北武穴人，教授、博士生導師。主要從事慣性系統及其標定測試、精確導航、新型慣導系統等方面的教學和科學研究。

Research on Auto-Compensation Technology of Random Error for Carouseling GINS

YANG Jianye1*，FAN Xiaohu1，ZHAO Xuyang1，WANG Lixin2

(1.The Second Artillery Engineering University，Qingzhou Shandong 262500，China; 2.The Second Artillery Engineering University，Xi’an 710025，China)

Based on the error propagating equations，the mathematical representation between navigation error and related functions of noise was obtained by using integral character.Random error propagating rule of Carouseling Gimbaled INS is explored，and the results thatthe platform’rotation could depress the typicalcolored noise while rotation angular velocity satisfied some condition and could not depress the white noise were obtained finally.Then it is proved thatthe theoreticalanalysis is feasible through simulation.The research provides certain theoreticalsupport for the engineering design and modification of GINS.

carouseling;GINS;radom error;auto-compensation

U666.12

A

1004－1699(2014)05－0637－06

2014-03-20

2014-04-17