基于L曲線法的抗差嶺估計模型

陳 帥,詹本勇

(1.天津市普迅電力信息技術有限公司,天津 300000；2.華能云南滇東能源有限責任公司白龍山煤礦,云南 曲靖 655508)

0 引 言

最小二乘法(又稱最小平方法)是一種數學優化方法,采用最小二乘原理進行的最小二乘估計(LS估計)具有良好的統計性質,但在當今工程測量及數據處理過程中,當自變量較多時,往往會使法方程的系數陣病態,使得采用LS估計求得的參數估值與真值相差比較大。再者,由于觀測值受到異常污染,使得觀測值中含有粗差時,因LS估計不具有抗粗差干擾的能力,也會導致最終求取的參數估值與真值偏差較大,甚至完全失真。當存在上述問題時,需要采用抗差有偏估計的方法進行處理[1]。

現有的抗差有偏估計方法主要有抗差嶺估計、抗差泛嶺估計等,上述方法在對受到系數陣病態及觀測粗差影響的參數估計取得了一定的成果,但大多數在迭代過程中采用的嶺參數與最小二乘嶺估計中的相同,而實際上在迭代過程中等價權是在不斷變化的,所以在每次迭代計算中應選擇最合適的嶺參數。嶺參數確定是影響估計結果非常重要的因素,因此,如何準確的選取嶺參數是抗差有偏估計方法的關鍵。

L曲線法[2]是確定嶺參數的一種有效方法,且在最小二乘嶺估計中已成功得到應用。本文采用中位數和標準化殘差構建抗差嶺估計模型[3],使用L曲線法進行嶺參數求解,通過迭代過程,最終選取精度最高、最合適的嶺參數。

1 數學模型

設參數平差的函數模型[4]為

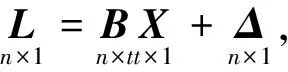
(1)

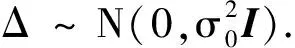
誤差方程為

(2)

由最小二乘原理可知,式(1)的最小二乘解為

(3)

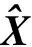
=min,

求得

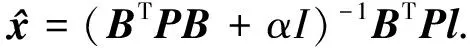
(4)

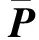
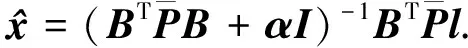
(5)

采用雙因子等價權模型[5],取

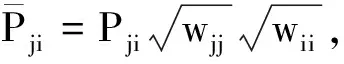
(6)

式中:wjj和wii表示自適應降權因子。由IGGⅢ計算得

wjj=

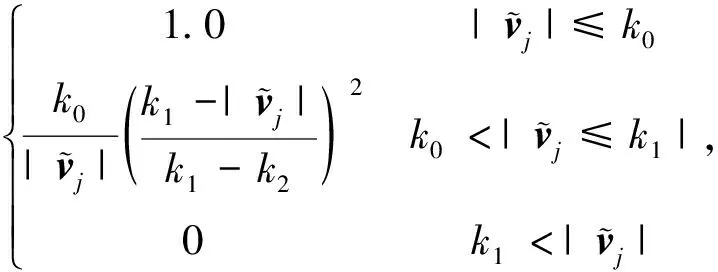
(7)

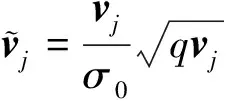
由式(2)和式(4)推導Qvv的計算公式為

Qvv=NggPNgg-2Ngg+P-1，

(8)

其中,Ngg=A(ATPA+αI)-1AT.

σ0為單位權中誤差,由中位數計算,計算公式為[6]

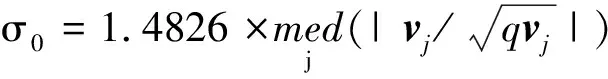
(9)

導出抗差嶺估計的迭代解式:

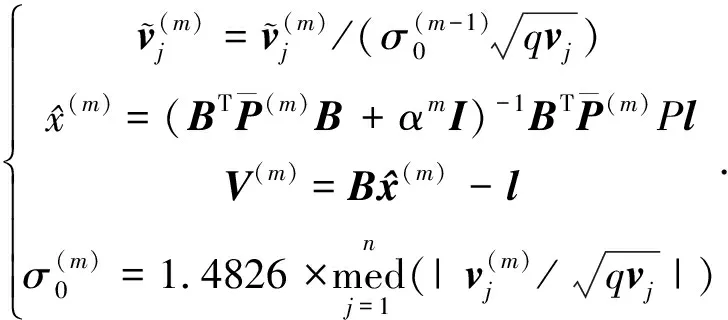
(10)

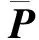
2 L曲線法求解嶺參數的基本原理

以對數形式推導,設

(11)

兩邊同時取對數,有

(12)

L曲線上各點的曲率可由下式計算[7]:

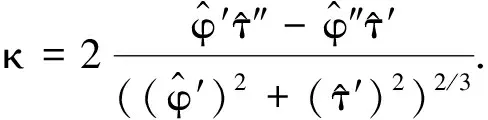
(13)

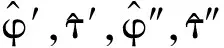
3 算例分析

設計病態矩陣為

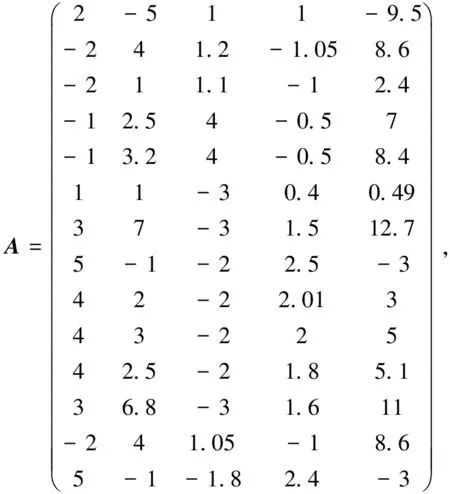
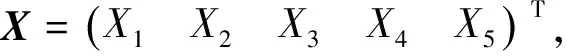
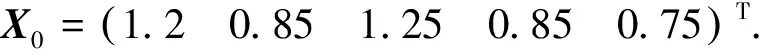
對數據做如下方案處理:

方案一:無粗差數據;方案二:將L1加入-5.5的模擬粗差;方案三:將L1、L14分別加入-5.5和-4.0的模擬粗差;方案四:將L1、L5和L7分別加入-5.5、-2.0和+4.5的模擬粗差;方案五:將L4、L12和L13分別加入+5.0、-3.0及+2.5的模擬粗差。

對上述無粗差數據及加入不同數量粗差的數據分別進行最小二乘估計、最小二乘嶺估計以及抗差嶺估計,通過三種不同方法求得的參數估計值的結果如表1所示。

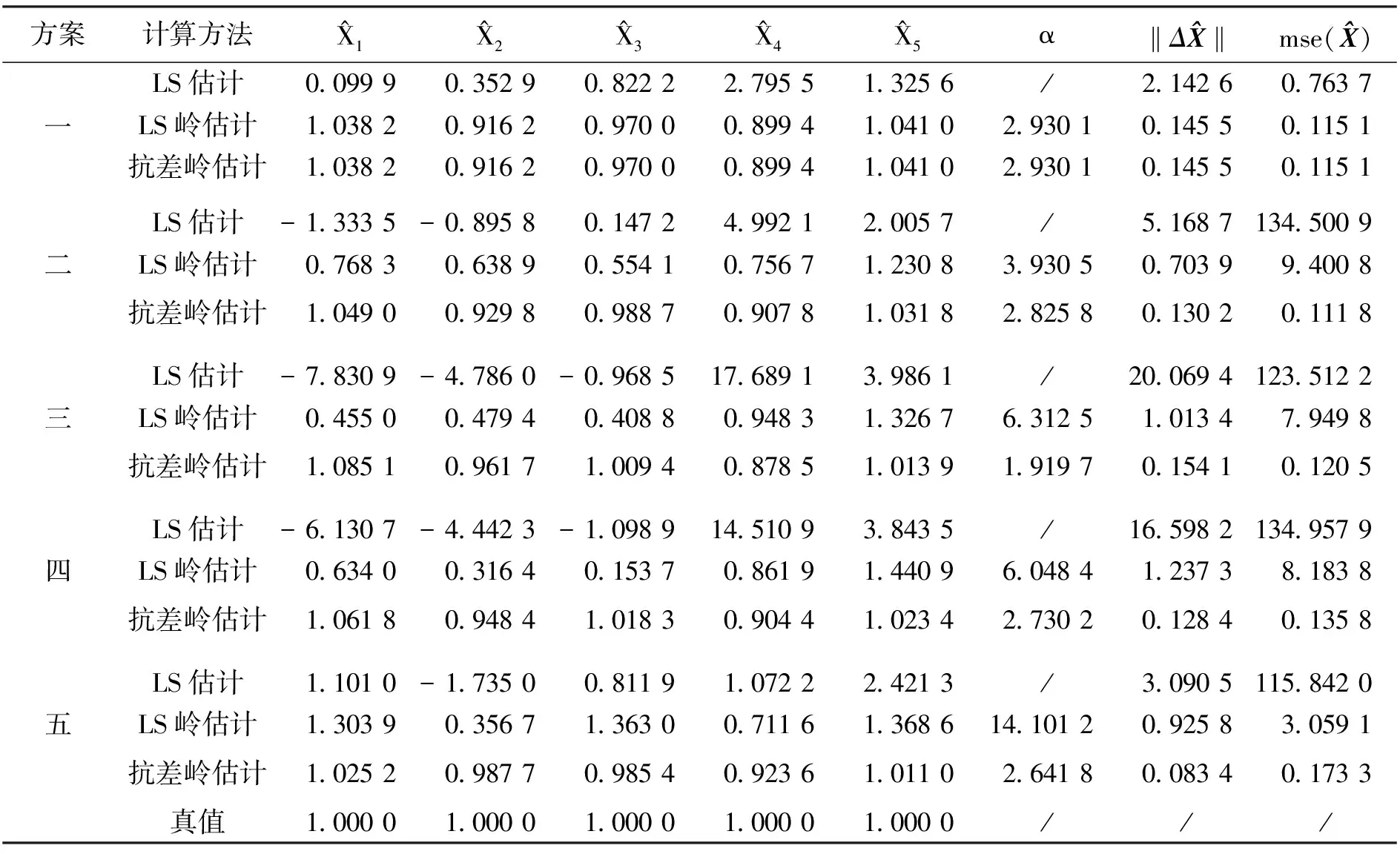
表1 五種方案的參數估計值對比表

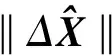
表2示出了加入粗差模擬的數據經最小二乘估計、最小二乘嶺估計以及抗差嶺估計后的殘差及權因子為零的觀測值序號。

表2加入粗差后的殘差值及相應觀測值序號統計表

方案零等價權觀測值序號LS估計殘差LS嶺估計殘差抗差嶺估計殘差模擬粗差數值 二1+4.076 2+4.139 7+5.722 7-5.5 三114+3.300 2+0.460 7+3.445 0+1.945 6+5.797 4+4.304 5-5.5 -4.0 1+3.027 8+3.192 4+5.761 3-5.5 四5+0.568 4+0.684 7+2.209 4-2.0 7-1.338 5-2.478 2-4.602 8+4.5 4-2.784 7-2.742 5-5.005 9+5.0 五12+1.131 6+2.153 9+3.147 0-3.013-1.547 9-1.700 8-2.303 3+2.5

通過以上計算結果的對比分析,可以看出:

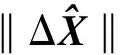
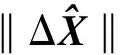
若在抗差迭代過程中始終使用LS嶺估計所采用的嶺參數則難以達到這樣的計算效果,這是由于在迭代過程中使用L曲線法選取適合每次迭代計算的嶺參數在理論上更加合理。

4)由于抗差嶺估計模型在迭代過程中采用的是L曲線法來確定嶺參數的值,與LS嶺估計模型中的嶺參數比較是變化的。圖1是采用L曲線法求解抗差嶺估計模型最終確定的嶺參數和LS嶺估計模型中的嶺參數的示意圖。

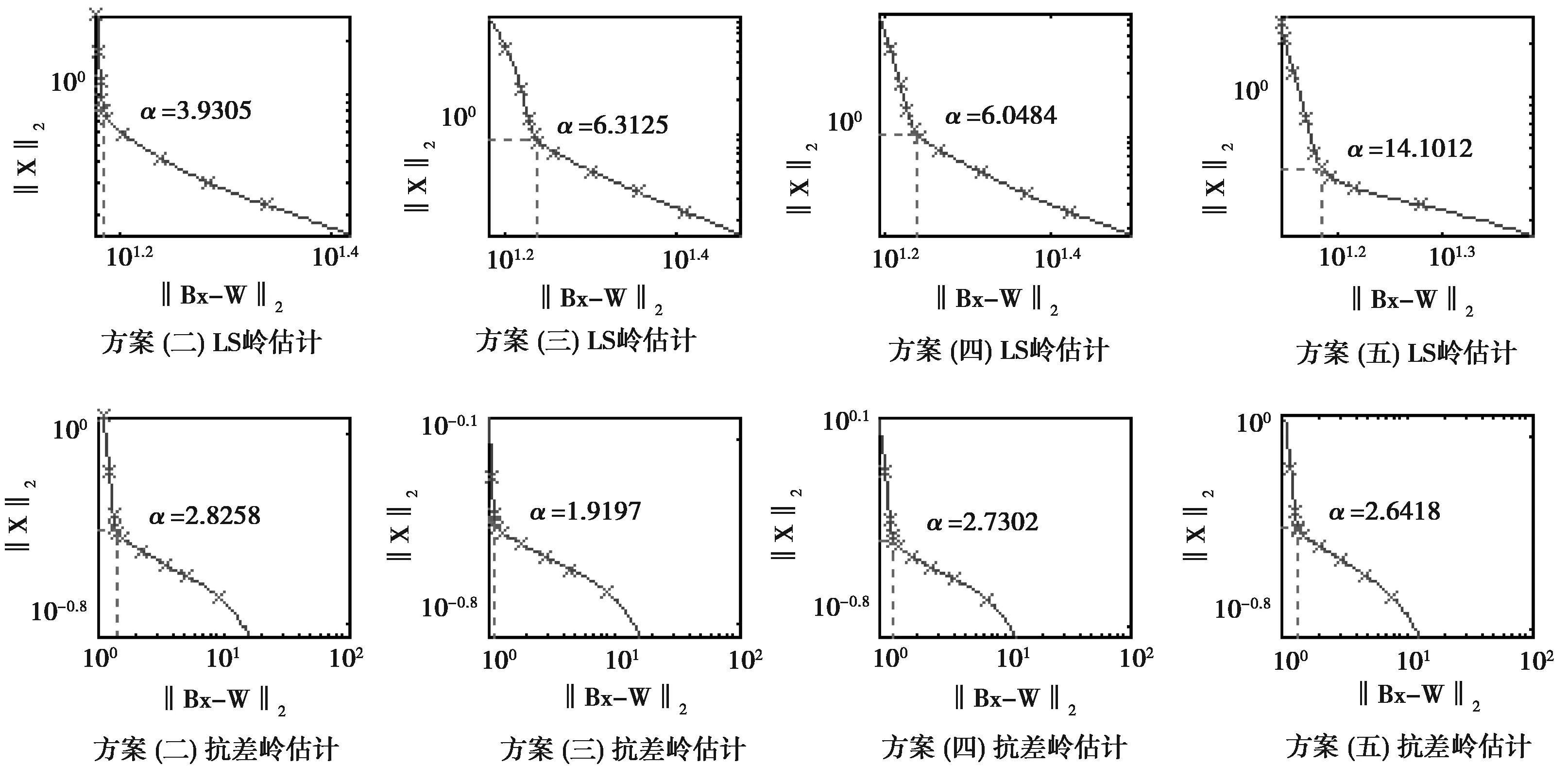
圖1 LS嶺估計與抗差嶺估計確定的嶺參數示意圖

4 結束語

由于受到系數陣病態以及觀測粗差的影響,采用經典最小二乘估計求取參數估值是極其不穩定的,導致最終的計算結果與真值偏差較大,這時需要采用抗差有偏估計的方法進行處理。文章介紹了抗差嶺估計模型,給出了關鍵公式的推導,并說明利用L曲線法求解抗差嶺估計模型中嶺參數的原理。最后結合實際算例作出五種方案的計算比較,通過對無粗差數據以及加入不同數量粗差的數據分別進行LS估計、LS嶺估計、抗差嶺估計,并對結果就行了詳細的分析,結果表明:LS估計不能夠克服系數陣病態的影響,抗粗差能力也非常弱;LS嶺估計雖然能夠有效的抵制系數陣病態的影響,但抗粗差能力也比較弱;與前兩種方法相比較,基于L曲線法的抗差嶺估計模型能夠有效的改善和抵制系數陣病態和觀測粗差帶來的影響。

[1]GUI Q, J. ZHANG J. Robust biased estimation and its applications in geodetic adjustments[J]. Journal of Geodesy, 1998(72):430-435.

[2]HANSEN P C. Analysis of discrete ill-posed problems by means of the L-curve [J]. SIAM Review, 1992, 34(4):561-580.

[3]王 彬,高井祥,王 堅,等.一種高精度GPS基線網抗差估計方法[J].全球定位系統,2011,36(3):39-42.

[4]隋立芬.抗差嶺估計原理及其應用[J].測繪通報,1994(1):7-8.

[5]YANG Y, SONG L,XU L. Robust estimation for correlated observations based on bifactor equivalent weights [J]. Journal of Geodesy, 2002(76):353-358.

[6]宋力杰.測量平差程序設計[M].北京:國防工業出版社,2009.

[7]王振杰,歐吉坤.用L-曲線法確定嶺估計中的嶺參數[J].武漢大學學報·信息科學版,2004,29(3):235-238.