Banach空間中H-η-單調算子的變分包含混合逼近點算法
王嫻,佟慧
(河北大學 數學與計算機學院,河北 保定 071002)
1 預備知識
變分包含是經典變分不等式的一個重要推廣,在許多領域(例如:物理學、最優控制、非線性規劃、經濟與工程學)中都有著廣泛的應用.因此,近年來,變分問題被諸多學者研究.
Verma發展了Eckstein-Bertsekas的關于A-極大單調算子[1]和(A,η)-極大單調算子[2]的混合逼近點算法.這些結論推廣了單值的極大單調算子,包含了文獻[3]中在Hilbert空間中關于H-極大單調算子的結論.目前,關于(A,η)-極大單調算子的廣義預解算法也已被介紹和研究.本文中,將文獻[4]結果推廣到了Banach空間,它和其他在Hilbert空間中討論的結果不同,這樣所得到的關于變分包含的結論就可以應用到Lp,Wm,p(Ω)空間中去.
設X是實的Banach空間,X*是其對偶空間,‖·‖表示X上的范數,〈·,·〉表示X和X*之間的配對,2X表示X的一切非空子集族.
廣義對偶映射Jq(x):X→2X定義為
Jq(x)={f*∈X*:〈x,f*〉=‖x‖p,‖f*‖=‖x‖q-1},q>1.
特別地,J2為正規對偶映射.眾所周知,Jq=‖x‖q-2J2,?x∈X.若X*為嚴格凸的,則Jq(x)為單值的.
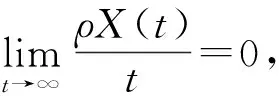
引理1[5]設X為一致光滑的實Banach空間,則X為q-一致光滑的當且僅當存在常數cq>0使得
‖x+y‖q≤‖x‖q+q〈y,Jq(x)〉+cq‖y‖q,?x,y∈X.
(1)
定義1[6]設M:X→2X*為多值算子,H:X→X*,η:X×X→X為單值算子,
1)稱X為單調的,如果〈x-y,u-v〉≥0,?u,v∈X,x∈Mu,y∈Mv.
2)稱M為η-單調的,如果〈x-y,η(u,v)〉≥0,?u,v∈X,x∈Mu,y∈Mv.
3)稱M為η-強單調的,如果存在某個常數r>0使得〈x-y,η(u,v)〉≥r‖u-v‖2,?u,v∈X,x∈Mu,y∈Mv.
4)稱M為m-松弛-η-單調的,如果存在某個常數m>0使得〈x-y,η(u,v)〉≥-m‖u-v‖2,?u,v∈X,x∈Mu,y∈Mv.
5)稱M為H-單調的,若M是單調的且對任何λ>0,(H+λM)X=X*.
6)稱M為(H,η)-單調的,若M是η-單調的且對任何λ>0,(H+λM)X=X*.
7)稱M為H-η-單調的,若M為m-松弛-η-單調的且對任何λ>0,(H+λM)X=X*.(在文獻[4]和[11]中H-η-單調算子被稱為(H,η)單調算子).
注1 在文獻[7]中首先介紹了η-單調算子,H-單調算子和(H,η)-單調算子,[8]中又介紹了H-η-單調算子.顯然,H-η-單調算子是(H,η)-單調算子的推廣.
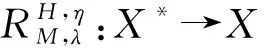
定義3[9-10]稱算子T:X→X*關于H°g為強增生的,如果存在某常數λ>0使得
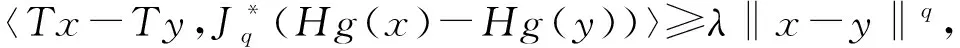
(2)
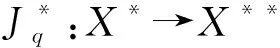
2 主要結論
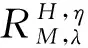
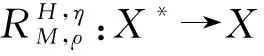

在定理1的基礎上來討論下面變分包含問題
f∈F(x,U(x))+M(g(x))
(3)
的解的迭代算法.其中x∈X,f,h∈X*,F:X×X→X*,g:X→X,U:X→X為3個單值算子,M:X→2X*為一個多值算子,關于它的非線性變分包含問題已在文獻[11]中考慮.顯然問題(3)包含了很多變分包含問題,見文獻[10].

(4)
其中ρ>0為常數.
證明:由定理1直接得到.
定理2 設X*為q-一致光滑的Banach空間,η:X×X→X為τ-Lipschitz連續算子,g:X→X為γ-強增生且t-Lipschitz連續的.H:X→X*為(r,η)-強單調且s-Lipschitz連續算子,U:X→X為ξ-Lipschitz連續算子.設M:X→2X*為H-η-單調多值算子.設F:X×X→X*為一個算子,使得對任意(x,u)∈X×X,F(·,u)關于H°g為強增生且σ-υ-Lipschitz連續的,F(x,·)為μ-Lipschitz連續的.對任意的給定的初值x0,構造如下序列{xk}:
xk+1=(1-αk)xk+αkyk,?k>0,
(5)
yk滿足
(6)
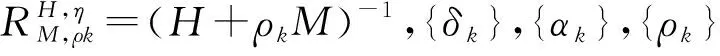
(7)
證明:由于g為γ-強增生的,故有
‖g(u)-g(v)‖‖u-v‖q-1=‖g(u)-g(v)‖‖Jq(u-v)‖q-1≥
〈g(u)-g(v),Jq(u-v)〉≥γ‖u-v‖q,
由上面的式子可知,g-1為單值算子且有
因此算法(5),(6)有意義.
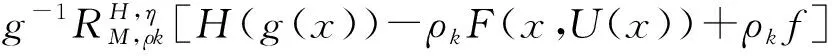
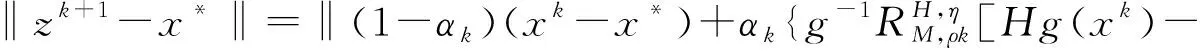
由假設和(2)得到
‖Hg(xk)-Hg(x*)-ρk[F(xk,U(xk))-F(x*,U(xk))]‖q≤
(8)
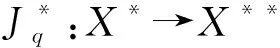
[1-αk(1-θk)]‖xk-x*‖=dk‖xk-x*‖,
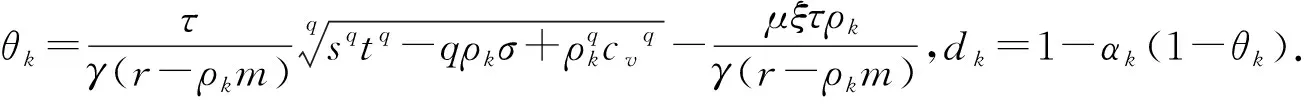
由xk+1=(1-αk)xk+αkyk,有xk+1-xk=αk(yk-xk),于是
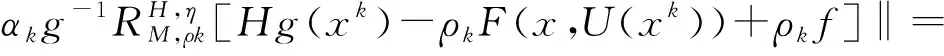
故有
‖xk+1-x*‖≤‖zk+1-x*‖+‖xk+1-zk+1‖≤‖zk+1-x*‖+αkδk‖yk-xk‖≤
‖zk+1-x*‖+δk‖xk+1-xk‖≤
‖zk+1-x*‖+δk‖xk+1-x*‖+δk‖xk-x*‖,
(9)
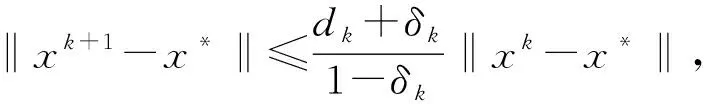

注2 條件(7)的證明可見文獻[10].
參 考 文 獻:
[1] VERMA R U. A-monotonicity and its role in nonlinear variational inclusions[J]. Optimization Theory and Applications, 2006,129(3) :457-467.
[2] VERMA R U. Sensitivity analysis for generalized strongly monotone variational inclusions based on the (A,η)-resolvent operator technique[J]. Applied Mathematics Letters, 2006,19: 1409-1413.
[3] FANG Yaping, HUANG Nanjing. H-monotone operators and system of variational inclusions[J]. Communications on Applications and Nonlinear Analysis, 2004,11(1):93-101.
[4] VERMA R U. A hybrid proximal point algorithm based on the (A,η)- maximal monotonicity framework[J]. Applied Mathematics Letters, 2008,21:142-147.
[5] XU H K. Inequalities in Banach spaces with applications[J]. Nonlinear Analysis, 1991,16(12):1127-1138.
[6] FANG Yaping, HUANG Nanjing. A new system of variational inclusions with monotone operators in Hilbert spaces[J]. Computers & Mathematics with Applications, 2005,49:365-374.
[7] HUANG Nanjing,FANG Yaping. Fixed point theorems and a new system of multivalued generalized order complementarity problems[J]. Applied Mathematics Letters, 2003,7:257-265.
[8] ZHANG Qingbang. Generalized implicit variational-like inclusion problems involvingG-η- monotone mappings[J]. Applied Mathematics Letters, 2007,20:216-221.
[9] FANG Yaping, HUANG Nanjing.H-Accretive operators and resolvent operator technique for solving variational inclusions in Banach spaces[J]. Applied Mathematics Letters, 2004,17:647-653.
[10] HOU Jian , HE Xinfeng, HE Zhen. Iterative methods for solving a system of variational inclusions involvingH-η-monotone operators in Banach spaces[J]. Computers & Mathematics with Applications, 2008,55:1832-1841.
[11] VERMA R U. Approximation solvability of a class of nonlinear set-valued variational inclusions involving (A,η)-monotone mappings[J]. Journal of Mathematical Analysis and Applications, 2008,337: 969-975.

