基于貝葉斯方法的單分類入侵檢測技術
肖仙謙,朱俊平,景旭,馬巧娥,2
(1.西北農林科技大學 信息工程學院,陜西 楊凌 712100;2.楊凌職業技術學院 信息工程學院,陜西 楊凌 712100)
入侵檢測就是對入侵行為的發現,收集計算機網絡或系統中的關鍵點信息并進行分析,從而判斷網絡或系統是否違反安全策略或被攻擊,是繼“加密機制”、“數據簽名機制”、“訪問和控制機制”、“認證機制”等傳統網絡信息安全技術的新一代網絡信息安全技術.
入侵檢測本質上是一個模式識別問題.很多傳統機器學習的方法被應用到入侵檢測中,如樸素貝葉斯、決策樹、支持向量機(SVM)等,一般都是同時對正負數據樣本進行訓練,從而得到分類器.但由于實際入侵檢測數據分布上的特殊性,即正常樣本數據量遠大于異常樣本數據量,因此系統對異常樣本的判斷能力不能很好地得到訓練[1].傳統的有監督學習不適合此問題.此時,入侵檢測問題可以被看成是數據描述(data description)或者是單分類(one-class)學習問題[2].
One-class學習算法的一個主要研究方向是基于統計密度估計.這些方法先對目標類建立變量統計模型,然后估計該模型的參數.而自從支持向量機(SVM)和核函數技術出現以來,在one-class學習中采用核函數的方法變得流行,其中包括one-class SVM模型[3-4]和支持向量數據描述[5],并且這2個方法被證明會產生同一個結果.但是,核函數技術一般不能利用數據中包含的領域知識;而且,也不能直接應用無標簽數據來提高準確率[6].所以,在傳統的支持向量數據描述(support vector data description,SVDD)模型基礎上,采用貝葉斯參數估計的方法對其進行改進,從而可以使上述問題得到解決.
文章將包含以下3方面,首先簡單介紹傳統的支持向量數據描述(SVDD);其次,介紹采用貝葉斯估計改進的模型,同時根據模型的特點,采用PCA技術對原始數據在各個方向上進行等方差處理,使之更加符合該模型,從而進一步提高檢測效果;最后,針對標準入侵檢測數據集NSL-KDD,對該模型進行測試,驗證該方法的正確性與有效性.其中包含2個創新點:一個是根據入侵檢測數據的不平衡性特點,將支持向量數據描述模型(單分類模型)應用到入侵檢測問題中;另一個是使用PCA技術對原始數據在各個方向上進行等方差處理,使得模型的檢測率得到較大的提高.
1 支持向量數據描述
支持向量數據描述(SVDD)是一種非常著名的基于核技術的單分類學習算法,希望在核空間中找到包含盡可能多的目標類數據,而其半徑又盡可能小的球面[7].由此可見,該模型在訓練時只需要目標類數據即可,并且該模型涉及到求解凸優化問題,這與SVM非常類似.此模型的具體介紹參見文獻[3],以下是其主要過程.
一個球面由其中心C和半徑R唯一確定.按照上述思想,再加上懲罰因子ζi,建立最優化模型如下:
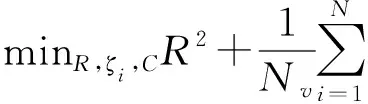
(1)
使得
‖φ(xi)-C‖≤R2+ξi且ξi≥0,
(2)
其中φ是核函數K(xi,xj)=<φ(xi),φ(xj)>中的變換函數,將數據映射到高維的核空間;變量v控制超球面體積與超球面中樣本數量的比例,同時,還可以控制最優化問題解的稀疏;N為目標類數據記錄的條數.
引入拉格朗日乘子,得到下面的對偶問題:
minααTΚα-αTdiag(Κ),
(3)
使得
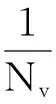
(4)
其中Κ是核矩陣,滿足Κi,j=<φ(xi),φ(xj)>; diag(K)是Κ的主對角線元素,不需要確定變換函數φ的具體表達式,而只需確定核函數即可.
該最優化問題的解是大部分為零的向量α.那些正的αi對應的樣本xi被稱為one-class SVM的支持向量.超球面的中心C可以由拉格朗日乘子從式(5)得到,
C=∑iαiφ(xi).
(5)
可以對各測試樣本到該中心的距離進行排序,距離越小,說明該樣本與目標類越接近.該距離函數化解后
f(z)=∑i∑jαiαjK(xi,xj)+K(z,z)-2∑iαiK(xi,z).
(6)
2 改進的支持向量數據描述
接下來從2方面對傳統的支持向量數據描述模型進行改進:一是利用PCA對原始數據在各個方向上進行等方差處理,使之更加符合模型的前提假設;二是利用貝葉斯參數估計對其進行改進,使得模型能夠充分利用入侵檢測數據所包含的先驗知識.
2.1 利用PCA進行數據預處理
數據集NSL-KDD來自數據集KDD CUP99的改進,其中每一記錄包含41個屬性以及1個類別標識.一般而言,利用PCA可以消除數據屬性間的相關性,從而減少數據量,加快訓練與檢測的速度[8].
另一方面,針對上述的支持向量數據描述問題,其根本目標是在核空間中尋找目標超球面.從而可見,如果該空間中的正例數據分布呈超球形,并且負例樣本位于超球形外部,則將有利于提高檢測準確率;反之,如果該空間中的正例數據分布呈超橢球形,將影響檢測率,并產生較大的誤檢率,如圖1所示.
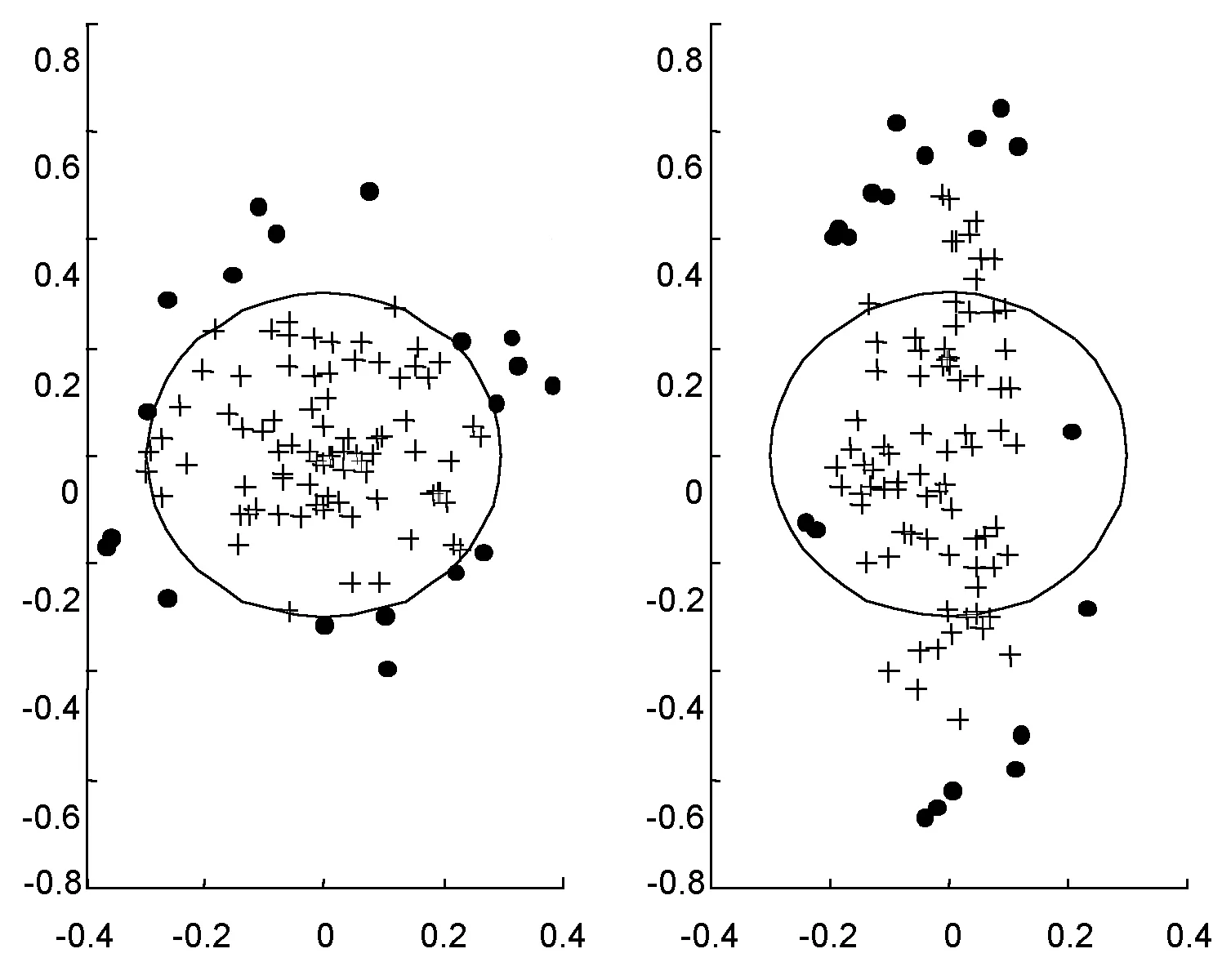
圖1 數據分布與檢測結果的關系Fig.1 Relationship between the data distribution and the detection results
因此,數據預處理的目標是使得核空間中目標類數據在各個方向上的分布一致.這可以由各個方向上數據的方差來近似衡量,即通過線性變換,使得處理后的數據在各個方向上的方差相等.例如,設一組一維數據X=x1,x2,…,xN,其方差為σ2,則X=x1/σ,x2/σ,…xN/σ的方差等于1.因此KPCA(kernel principal component analysis)[9-10]在理論上可以解決該問題.然而KPCA計算復雜度與數據記錄的個數有關,在計算上存在應用困難.因此,考慮針對原空間數據采用PCA技術,同時采用映射前后數據分布仍然呈超球形的核函數,如線性核函數、高斯徑向基函數(RBF)核函數等.接下來介紹如何應用PCA技術來處理原始數據,從而使得處理后的數據滿足上述要求.
在PCA中,假設原始數據矩陣Y具有m個屬性,num個記錄,變換后的數據矩陣Z具有n個屬性,num個記錄,且應滿足n≤m,則
Zn×num=UTYm×num,
(7)
其中U=[u1,u2,…,un],ui,i=1,2,3,…,n對應特征值λi的特征向量,且λ1>λ2>…>λn為所取的前n特征值.令Z=[z1,z2,…,zn]T,則求解特征方程得到的各個特征值λi即為各個方向zi上的方差,所以,將經過PCA變換后的數據除以對應的特征值的開方,這樣變換后得到的數據D將滿足上述方差相等的要求,
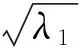
(8)
所以,令D=PY,則
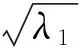
(9)
由上述得到的數據矩陣D各個屬性的方差均等于1.而在實際應用中,只需保證其方差相等即可;并且根據實驗發現,不同大小的方差將對檢測結果產生影響,因為最終的變換公式為
D=σPY,
(10)
其中σ等于數據矩陣D各個屬性的標準差,實驗中將作為參數出現.
2.2 貝葉斯參數估計
支持向量數據描述模型的主要思想為尋找核空間中的超球面中心C,見式(5).基于數據分布的合適假設,可以根據給定的數據,利用貝葉斯參數估計對式(5)中的參數αi,i=1,2,3,…,N進行參數估計,從而獲得超球面的中心.利用貝葉斯參數估計對模型改進,一方面與入侵檢測數據的隨機性相吻合,另一方面可以更加充分地利用數據中包含的信息[11].
該改進模型基于以下2點假設.1)假設經過變換函數φ將原始數據映射到高維核空間后的數據服從高斯分布,且其協方差矩陣為單位向量I,均值向量為超球面中心C,
φ(xj)~N(∑iαiφ(xi),I),
(11)
其中限制0<αi<1且∑iαi=1,從而保證其構成一個凸集.2)根據貝葉斯參數估計理論,關于參數向量α的先驗概率分布p(α)需被定義,假設參數向量α服從高斯分布,其均值為m,協方差矩陣為Cov,
α~N(m,Cov).
(12)
根據以上2點假設,對參數向量α進行貝葉斯參數估計.根據假設2)確定了關于向量α的先驗概率分布p(α),而后驗概率p(α|D)由貝葉斯公式可以得到
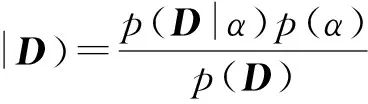
(13)
其中D表示由原數據映射到核空間中的數據,p(D|α)是已知α下訓練數據的似然性.其中p(D)為常數.根據貝葉斯估計中的最大后驗概率估計,以及2個假設確定的數據分布,將得到以下二次最優化問題,
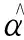
(14)
使得
0<αi<1,∑iαi=1,
(15)
其中矩陣Κ是核矩陣,矩陣D是樣本的加權度對角矩陣,滿足Dij=∑jΚij,向量1表示元素全為1的向量.這就是使用貝葉斯方法改進后的單分類數據描述模型,記為BDD(bayesian data description),其中的參數m和Cov可以由用戶設定.可以發現,當設定Cov=I,m=diag(Κ)-D1,此時模型即為原來的SVDD模型.而且,該模型最后與變換函數φ無關,從而很好的應用了核技術.
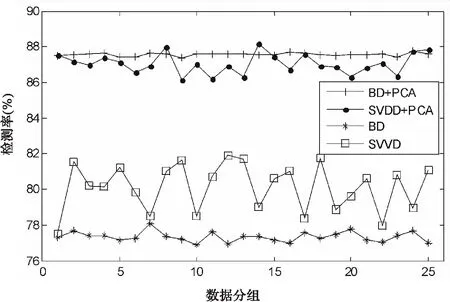
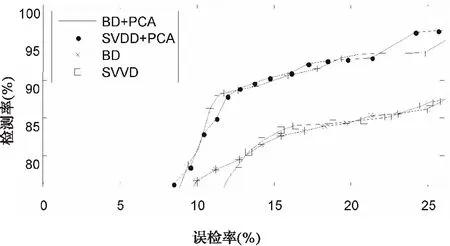
進行貝葉斯參數估計時,確定參數合理的先驗概率分布非常重要.根據數據的密度與α的相關性確定其先驗分布的均值[12].其中參數0 mi=-(∑jΚi,j)v. (16) 該模型求解的計算復雜度與數據記錄的個數相關,所以在建立該模型時,一次使用的數據量不能太大.然而,根據假設A)知,核空間的所有數據服從協方差矩陣為單位矩陣的正態分布,記作N(*,I).采用分治的算法思想,將所有數據隨機等分成k組數據,得到k個模型,即k個協方差矩陣為單位矩陣的正態分布,Ni(*,I),i=1,2,…,k.根據正態分布線性變換的正態性,該k個正態分布的均值服從正態分布,這里就應該等于N(*,I),即式(17)成立,這樣就可以解決上述問題. (17) 由以上過程,即可得到對數據中心C表達式中的參數α,從而可以根據式(6)求解各個數據記錄到中心C的距離.分析發現其計算復雜度與參數向量α的稀疏性有關,所以控制解稀疏性的參數v的選擇對訓練的效率將有較大的影響. 為了尋找距離確定的分類閾值,原文采用的是一種簡單的實驗性方法;它將各個距離排序后,選取想要的數據記錄的個數,存在很大的主觀性.因此,這里基于該距離序列,采用SVM進行訓練[13-14],從而確定分類器.而且由于此時訓練數據為一維數據,所以會有較高的訓練效率. 實驗采用NSL-KDD數據集,其中訓練數據與測試數據均包含41個屬性,包括離散屬性與連續屬性,使用weka對其進行處理,將其中的離散屬性數值化,之后把所有41個屬性的數據規范化到[0,1]范圍內.同時,每條記錄包含一個類別標識,記錄攻擊名稱或者正常,這里將它二值化,即正常或異常.選擇的訓練數據來自文件KDDTrain±20Percent.txt,測試數據來自文件KDDTest+.txt;訓練數據包含25 192條記錄,其中的13 449條正例樣本為建立模型所需要的,測試數據包含22 544條記錄.相比于原來的KDD CUP 99數據集,NSL-KDD對入侵檢測算法的要求更高. 實驗需設置以下參數:控制解稀疏性的參數,數據分組數,PCA處理后的標準差,核函數及其參數等.對于控制解稀疏性的參數和標準差,采用經驗值,取v=0.9,σ=30.根據實驗發現,建立模型時所需的數據數量達到一定大小后,實驗結果將趨于穩定,因此,根據實驗結果,這里將13 449條正例數據分成K=25組較為合理.考慮數據正態分布的假設,所以全部采用高斯徑向基函數(RBF)作為核函數,對應核參數設定為1. 圖2中的實驗,針對訓練數據的各分組分別建立求解SVDD,SVDD+PCA,BBD和BBD+PCA模型.由圖2可見,單分類模型SVDD與BD模型都可以獲得較好的檢測效果;并且通過PCA技術對數據在各個方向上進行等方差處理后,使得檢測準確率有明顯的提高.同時,在SVDD模型與BD模型間進行對比發現,BD模型的檢測結果明顯比SVDD模型穩定.最后計算得出PCA+BBD模型的平均檢測率為87.46%. 圖2 各組數據下各類模型的檢測準確率比較Fig.2 Comparison of detection rate with each group data set by different model 通過比較模型之間的ROC曲線可以進一步衡量入侵檢測模型的性能[15].為了得到各個模型的ROC曲線,需要為模型設定不同的分類閾值.其主要過程為:在使用正例數據完成了模型的建立之后,將各個正例樣本到模型中心的距離進行排序,然后均勻選取50個樣本,將該50個樣本到模型中心的距離作為分類閾值,從而得到對應的檢測率與誤檢率. 圖3顯示了針對訓練數據的某個分組分別建立求解SVDD、PCA+SVDD、BBD和PCA+BBD模型得到的ROC曲線.由圖3可見,BD+PCA與SVDD+PCA模型下入侵檢測系統的性能明顯高于改進前的BD與SVDD模型,并且此時的BD+PCA模型與SVDD+PCA模型性能非常接近,不過由圖2對應的實驗可知,BD+PCA模型對不同的訓練數據,穩定性更高. 圖3 各類模型的ROC曲線比較Fig.3 Comparison of ROC curve between different model 表1顯示了針對同一數據集,其他經典方法[16]的檢測率.與這些基于有監督學習的經典二分類方法的不同之處是,本文提出的模型是一種單分類模型[17],并且在模型建立時所需的樣本數量更少;一般而言,二分類使用了更多的數據,在檢測結果上應該優于單分類模型.比較表中數據發現,本文提出的模型的檢測率更高.而如果再找到更加合適的方法來代替模型中的SVM訓練,則此模型將成為理想的半監督入侵檢測模型. 表1 各類經典方法的檢測率比較 在入侵檢測技術的研究中,對二分類或多分類模型研究的較多,而單分類模型則幾乎未曾涉及.根據實際網絡中數據的不平衡性,即正常樣本數據遠遠大于異常樣本數據,所以有必要對這種單分類模型進行研究.本文對原單分類數據描述模型進行改進,并將它應用于入侵檢測中,提高了入侵檢測的效果.接下來希望尋找合適的方法代替其中的SVM訓練,使模型訓練時不需要知道數據的標簽,從而將該模型改進成半監督模型,同時還希望減少模型的誤檢率,并考慮將其應用到實際的網絡中. 參 考 文 獻: [1] ALIREZA Ghasemi,HAMID R Rabiee, MOHAMMAD T Manzuri, et al.A Bayesian approach to the data description problem[C]. Proceedings of the Twenty-Sixth AAAI Conference on Artificial Intelligence, California:AAAI Press, 2012,907-913. [2] DOROTHY E D. An intrusion detection model[J]. IEEE Transactions on Software Engineering, 1987,13(2):222-232. [3] SCHLKOPF B, PLATT J C,TAYLOR J S, et al. Estimating the support of a high dimensional distribution[J]. Neural Computation,2001,13(7):1443-1471. [4] 黃謙,王震,韋韜,等. 基于One-class SVM的實時入侵檢測系統[J].計算機工程,2006,32(16):127-129. HUANG Qian, WANG Zhen, WEI Tao, et al. A real-time intrusion detection system based on One-class SVM [J]. Computer Engineering, 2006, 32(16):127-129. [5] TAX D, DUIN R. Support vector data description[J]. Machine Learning, 2004,54(1):45-66. [6] SHEHROZ S Khan, MICHAEL G Madden. A survey of recent trends in one class classication[J]. Artificial Intelligence and Cognitive Science, 2010,45(16):188-197. [7] PORTNOY L, ESKIN E, STOLFO S. Intrusion detection with unlabeled data using clustering[C].DANIEL Barbara, SUSHIL Jajodia. Proceedings of 2001 ACM CSS Workshop on Data Mining Applied to Security, Philadelphia:[s.n.],2001. [8] BEN H A, GUYON I. Detecting stable clusters using principal component analysis[C]. MICHAEL J Brownstein, APKADY B Khodursky. Methods In Molecular Biology, CLIFTON, 2003. [9] 許國根, 賈瑛. 模式識別與智能計算的MATLAB實現[M]. 北京:北京航空航天大學出版社,2012. [10] 包潘晴,楊明福.基于KPCA和SVM的網絡入侵檢測[J].計算機應用與軟件,2006,23(2):125-127. BAO Fanqing,YANG Mingfu. KPC and SVM based network intrusion detection[J]. Computer Applications and Software,2006,23(2):125-127. [11] ISABELLE GUYON, ANDRE ELISSEEFF. An introduction to variable and feature selection[J]. Journal of Machine Learning Research,2003,3:1157-1182. [12] YE Nong, LI Xiangyang, CHEN Qiang, et al. Probabilistic techniques for intrusion detection based on computer audit data[J]. IEEE Transaction on Systems, Man and Cybernetics,2001,31(4):263-271. [13] 邊肇琪,張學工. 模式識別[M].北京:清華大學出版社,2000. [14] CHANG Chihchung, LIN Chihjen. LIBSVM: A Library for Support Vector Machines[DB/OL].[2013-3-14]http://www.csie.ntu.edu.tw/~cjlin/papers/libsvm.pdf. [15] 田俊峰,劉濤,陳小祥. 入侵檢測系統的評估方法與研究[J].計算機工程與應用,2008,44(9):113-117. TIAN Junfeng, LIU Tao, CHEN Xiaoxiang. Survey in evaluation of intrusion detection system[J]. Computer Engineering and Applications,2008,44(9):113-117. [16] MAHBOD Tavallaee, EBRAHIM Bagheri, WEI Lu,et al.A detailed analysis of the KDD CUP 99 Data Set[C]. 2009 Second IEEE Symposium on Computational Intelligence for Security and Defense Applications (CISDA),[s.n.],2009. [17] HODGE V, AUSTIN J. A survey of outlier detection methodologies [J]. Artificial Intelligence, 2004,22:85-126.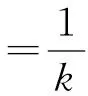
3 實驗與結果分析

4 結論

