民辦獨立學院線性代數教學現狀分析及改革研究*
蔡 劍
(南京航空航天大學金城學院,江蘇南京 211156)
民辦獨立學院線性代數教學現狀分析及改革研究*
蔡 劍
(南京航空航天大學金城學院,江蘇南京 211156)
民辦獨立學院課程的教學模式通常照搬母體本科高校,在教學中易出現“水土不服”現象,因此有必要針對民辦獨立學院學生的特點,探索合理的教學模式.以邏輯性、抽象性較強的基礎課程線性代數教學為例,提出了以理論與實踐相結合的教學主線為牽引,在教學中融入數學建模思想,增加實驗教學環節的教學新模式,不斷激發學生學習線性代數的興趣,提高民辦獨立學院線性代數課程的教學質量.
線性代數;教學;改革
1 現狀分析
民辦獨立學院始于上世紀90年代末期,是由本科高校與社會力量聯合辦學,進行本科層次教育的機構.獨立學院的教學模式通常與母體本科高校保持一致.獨立學院招收的生源主要集中在二本線與三本線之間,而母體本科高校的生源高考分數通常在一本線以上.由于獨立學院與母體本科高校學生的學習習慣、學習能力及學習基礎均存在較大差異,簡單照搬母體本科高校的教學模式,在教學過程中容易出現兩級分化嚴重、不及格率過高等教學“水土不服”現象,制約了民辦獨立學院教學質量的進一步提高.為了解決由照搬教學模式產生的問題,必須針對獨立學院課程與學生的特點開展研究,因地適宜、因材施教,形成合適的課程教學模式[1,2].
線性代數是民辦獨立學院與母體本科高校均開設的一門基礎課程,它集理論性和實踐性于一體[3-5],是許多專業課程的理論基礎,該課程的學時通常為32~40學時.母體本科高校在講授該課程時,通常將授課重點集中在抽象理論的證明與推導上,對于教材中的實踐案例通常由學生課后拓展.由于母體本科高校學生數學基礎扎實、自學能力較強,該教學模式獲得了較好的教學效果.照搬母體本科高校線性代數主理論、輔實踐的教學模式顯然不適合民辦獨立學院,因此有必要在課程學時不變的條件下,探索教學中兼顧理論與實踐新模式.
本文在分析民辦獨立學院教學模式現狀基礎上,以線性代數課程為例,提出一種新的課程教學模式.該模式將線性代數課程的理論知識與實踐背景結合成教學主線,在教學過程中以主線為牽引協助學生理解,并在理論與實踐教學中滲透數學建模思想,增設數學實驗等教學環節,豐富教學形式,激發學生學習興趣,提高學生學習效率.通過教學模式改革加強民辦獨立學院教學中的實踐能力培養,提高線性代數課程教學質量,形成適合民辦獨立學院的教學模式.
2 改革研究
2.1 建立以理論與實踐相結合的教學主線
建立教學主線,有助于學生建立知識點之間的聯系,協助知識點記憶與應用.線性代數課程如能建立一條教學主線,將繁多的理論知識聯系在一起,勢必可以大幅提升學生的理解能力,便于抽象理論知識的理解與應用.
以同濟大學數學系編寫的線性代數教材為例,教學內容的章節依次是:行列式、矩陣及運算、矩陣的初等變換與線性方程組、向量組的線性相關性、相似矩陣及二次型[6].從章節名稱上看,每個章節都是沒有聯系的新知識,若在教學中不將上述章節通過主線串聯,學生在上述章節知識學習中很難發現各章節知識的聯系,使知識點難以理解與記憶,不斷開啟的新章節還會沖淡已學習的知識,使學生在線性代數學習中不斷產生挫敗感,從心理上對課程產生畏懼.如果教師在授課過程中將知識點以教學主線牽引,使學生沿著教學主線學習,將每一章內容均作為主線上的分支,那么勢必會顯著改善教學效果,增加學生學習的信心.
從線性代數教材所排列的各個章節知識點的理論與實踐角度分析,線性代數教材中各個章節的理論知識均以“線性方程組的求解”作為實踐目的,因此以“線性方程組的求解”作為教學主線,可以使學生了解每一章知識的用處,比較每一種求解方法的區別,有助于學生對知識點的記憶與應用.
在教學過程中,除了教師由上向下灌輸“線性方程組的求解”的教學主線外,還要在知識點學習中不斷證明該教學主線的存在,讓學生逐步體會該教學主線.
以第一章教學內容中的克拉默法則、第二章教學內容中的矩陣、第三章教學內容中的矩陣的初等變換教學內容為例,將三章內容依據“線性方程組的求解”的教學主線串聯,可以采用以下教學模式.
首先,在教學中介紹克拉默法則,已知n個未知變量n個方程的線性方程組
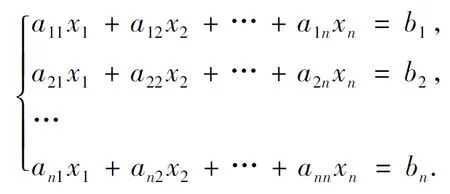
如果系數行列式D≠0,則該方程組有解,并且有唯一的解.
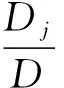
通過克拉默法則知識點的學習將知識點與線性方程組求解建立聯系,將該知識點的學習作為求解線性方程組的一種分支方法.同時引導學生思考該法則的適用范圍,讓學生思考“系數行列式D=0”、“未知量的個數與方程的個數不同”兩種條件下克拉默法則能否求解方程組?該問題的回答顯然是否定的.
通過克拉默法則的教學使學生了解學習知識點的作用,并熟悉知識點用于求解線性方程組的條件,從而引出后續矩陣章節的知識點.
其次,在行列式章節學習后進行矩陣、矩陣的初等變換等知識點學習,將矩陣、矩陣的初等變換與線性方程組的求解再次建立聯系,該過程可以通過一個算例來具體描述,算例如例1所示.
例1 求線性方程組

的解.
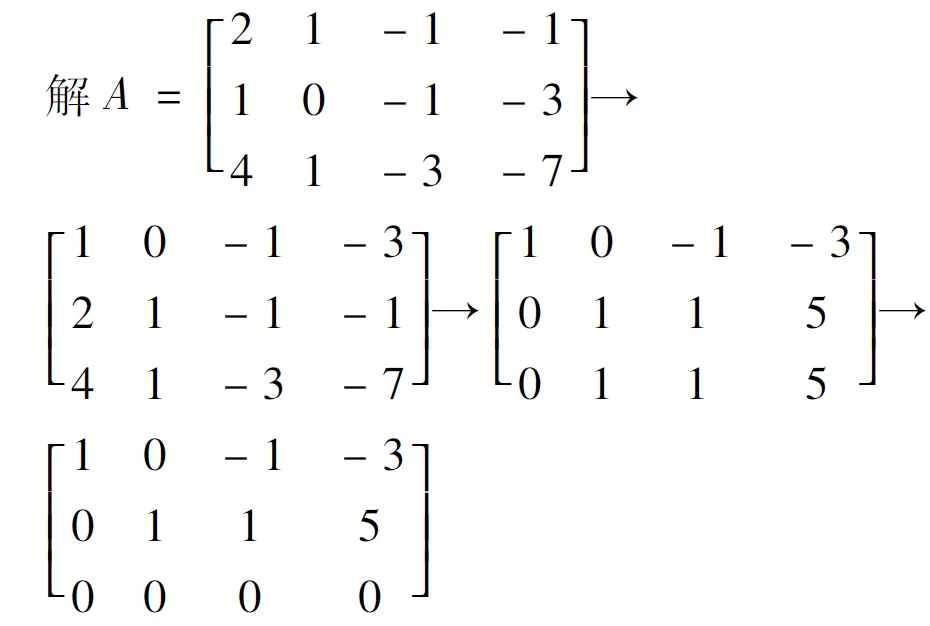
則方程組的解為

其中x3,x4為自由未知量.
在算例教學中,引導學生回憶前面章節所學的克拉默法則知識點.該方程用克拉默法則無法求解,但是可以通過矩陣的初等變換求解,獲得的解為含有未知量的解的表達式,賦予未知量不同值可以獲得無窮多組解.
通過克拉默法則與矩陣、矩陣初等變換的比較教學,反復強調“線性方程組的求解”的教學主線,使學生加深對知識點的認識,建立起知識點之間的聯系.
以理論與實踐結合為教學主線的教學模式,有助于理清抽象知識點相互之間的聯系,由淺入深、側重實踐,既考慮到學生的數學基礎,又兼顧民辦獨立學院培養人才的目標,有助于線性代數課程教學質量的進一步提升.
2.2 理論聯系實踐,在教學中滲透數學建模思想
民辦獨立學院的辦學目的主要是培養應用型、實踐型人才,因此在教學過程中應該重點突出課程知識點的應用與實踐.線性代數課程理論知識較為抽象,但其知識點已在工程各大領域廣泛應用,為了能使民辦獨立學院學生迅速將知識點學以致用,可以在課程教學中引入以線性代數知識為基礎的數學建模實例,培養學生將知識點應用于實踐的能力.
例如,在進行特征向量教學過程中,可以引入以下數學建模算例.
例2經過統計,某森林啄木鳥和蛀蟲的數量具有如下規律:如果沒有蛀蟲做食物,每個月只有一半的啄木鳥可以存活,如果沒有啄木鳥作為捕食者,蛀蟲的數量每個月會增加10%,如果蛀蟲充足(數量為R),則下個月啄木鳥的數量將會增加0.4R.平均每個月每只啄木鳥的捕食會導致104只蛀蟲死亡.試確定該系統的演化情況.
(1)模型假設
不考慮其他因素對啄木鳥和蛀蟲的數量的影響.
(2)模型建立

Ok+1=0.5Ok+0.4Rk,
Rk+1=-0.104Ok+1.1Rk,
分析xk的變化趨勢.
(3)模型求解


則初始向量x0=c1ξ1+c2ξ2.
于是,對于k≥0,
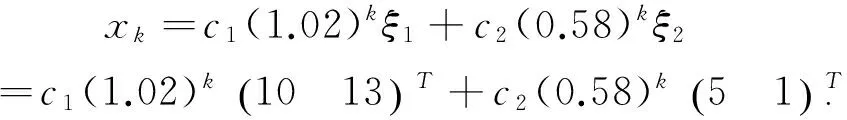
當k→時,(0.58)k迅速地趨向于0.假定c1>0,則對于所有足夠大的k,xk近似地等于c1(1.02)kξ1,即

k越大近似程度越高,所以對于充分大的k,

(4)模型分析
上面等式表明,最后啄木鳥和蛀蟲的數量幾乎每個月都近似增加到原來的1.02倍,即有2%的月增長率.而且Ok與Rk的比值約為10比13,即每10只啄木鳥對應著約13000只蛀蟲.
運用具體例子將直觀性和應用性滲透到線性代數的教學中,可以使教學更生動,更具科學性,使學生對抽象的理論有透徹的理解,所以在線性代數課程中融入數學建模能有效提高教學質量.
2.3 增加數學實驗課
線性代數課程習題數據計算量大,非常考驗學生的耐性與專注力,該課程學時少,而上課又要兼顧理論和計算的問題,往往使學生疲于應付.
若將MATLAB等專業數學軟件應用引入線性代數課程教學,可以使學生從繁重的計算任務中解脫,將精力專注于實際問題的建模,從而增加學生解決實際問題的成就感,激發學生學習的興趣.
在線性代數課程的教學中,演示一些MATLAB編程計算實例,例如高階行列式的計算、“圖像壓縮等技術”等實際問題舉例,讓學生充分認識到線性代數課程知識是未來學習與工作中的重要基礎,使學生對該課程的學習產生更多的興趣.
3 結束語
民辦獨立學院的線性代數課程教學不能照搬母體本科高校的教學模式,應當針對獨立學院培養人才的目標與學生的基礎尋找合適的教學模式.本文提出的課程教學模式,主要是以理論與實踐結合形成教學主線,在教學中融入數學建模思想、增加實驗課程,使課程理論學習與實踐并重,培養學生運用線性代數知識解決實際問題的能力,激發學生的學習興趣,提升線性代數課程教學質量.
[1]杜建衛,蘇欣.讓線性代數課程易教易學[J].大學數學,2011(5).
[2]王利東,劉婧.從應用實例出發的線性代數教學模式探討[J].數學教育學報,2012(3).
[3]趙慧斌.問題驅動是線性代數有效的教學法之一[J].高等數學研究,2008(4).
[4]李小平.關于《線性代數》教學改革的一些思考[J].大學數學,2011(3).
[5]李尚志.線性代數教學改革漫談[J].教育與現代化,2004(1).
[6]同濟大學數學教研室.線性代數[M].北京:高等教育出版社,2009.
(責任編輯 張建軍)
] 南京航空航天大學金城學院教學改革項目“金城學院《線性代數》課程教學現狀分析及教學改革研究”(項目編號:2013-Y-11).
2014-07-09
蔡 劍,女,江蘇靖江人,南京航空航天大學金城學院講師,碩士.
O151
A
1671-1696(2014)11-0033-03
* [

