The Diffusion Relaxation Approximation of the Incompressible Navier-Stokes Equations

LIU Yanhui，YANG Jianwei

(1.Faculty of Science，Hunan Institute of Engineering，Xiangtan 411104，Hunan；2.College of Mathematics and Information Science，North China University of Water Resources and Electric Power，Zhengzhou 450011，Henan)

1 Introduction

Let us consider the following system

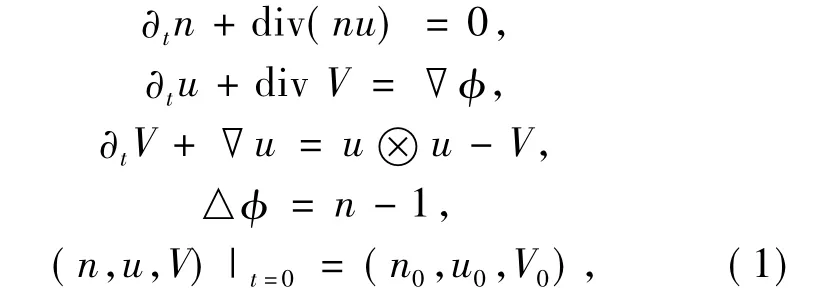
for(x，t)∈T2×［0，T］，whereT2=(R/Z)2is the unit periodic square.The unknowns aren∈R，u∈R2，V∈R2，2and φ∈R.

Now，let us consider a diffusive scaling，namely，for τ＞0，we set

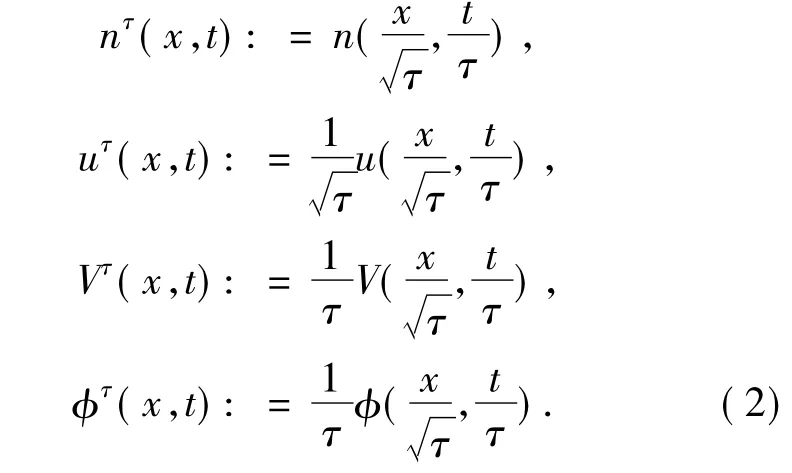
Therefore system(1)becomes

In this paper we shall prove that，under some suitable assumptions，the solutions to(3)converge，when τ goes to 0，to the(smooth)solutions of the incompressible Navier-Stokes equations

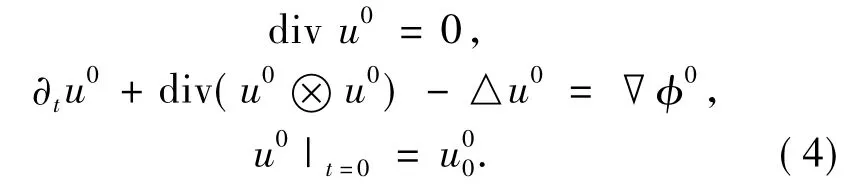
The aim of this note is to give a rigorous justification to this formal computation by using the hyperbolic energy method.

There have been a lot of studies on the diffusive scalinghas been largely investigated in the framework of hydrodynamic limit of the Boltzmann equation［1］and in the analysis of hyperbolic-parabolic relaxation limits for weak solutions of hyperbolic systems of balance laws with strongly diffusive source term［2-3］.Brenier et al［4］study the relaxation approximation of the incompressible version of present relaxation system by using the modulated energy method.For other diffusive relaxation models and some useful results，the reader is refered to［5-11］.

Here we state the main differences between the present paper and ［7］.First，the convergence rates obtained in two papers are different.Second，the new unknowns introduced by us are also different from［7］.Therefore，each equation of the error system in present paper involves singular term which is different from［7］.Finally，we give the convergence rate forVwhich has not been given in［7］.We noticed that the method used in［7］can also obtain our result.

2 The main result

In this section，we state our main theorem.For this，we first recall the following classical result on the existence of sufficiently regular solutions of the incompressible Euler equation［12-13］.

3 Proof of theorem 2.1

3.1 Reformulation of the system with new unknownsAs in［14］，we define the new unknownsn1，d1，ω1，D1，Ω1as

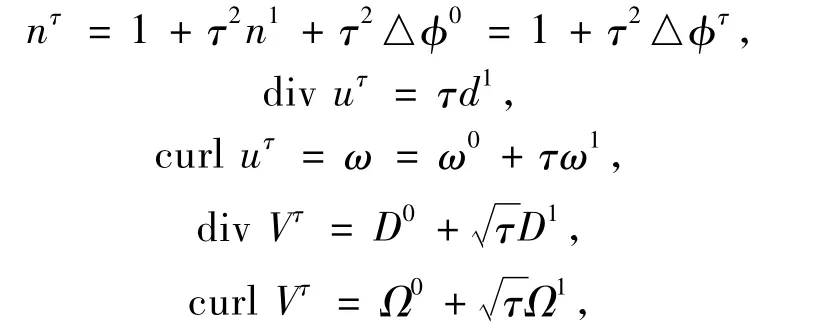
with(u0，φ0)the solution of(4)，and ω0=curlu0.Moreover，D0=divV0and Ω0=curlV0.Note that by taking the divergence of the second equation in(4)the pressure is given by

Then，from system(3)we know the vector(n1，d1，ω1，D1，Ω1)solves the system

Here，we have used the fact that

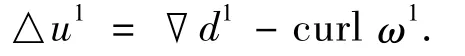
3.2 Energy estimatesFor|α|≤s-1 withs≥4，let us set

Taking theL2inner product of the equations in(8)with，respectively，one gets，by integration by parts and using Cauchy-Schwartz's inequality，Sobolev's lemma，basic Moser-type calculus inequalities［15］that

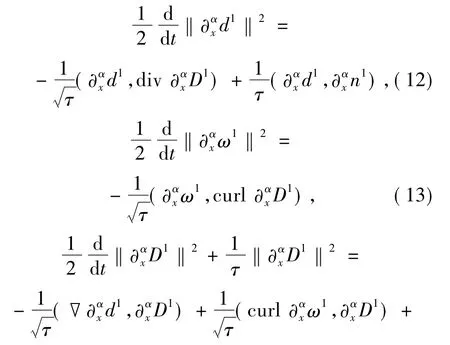
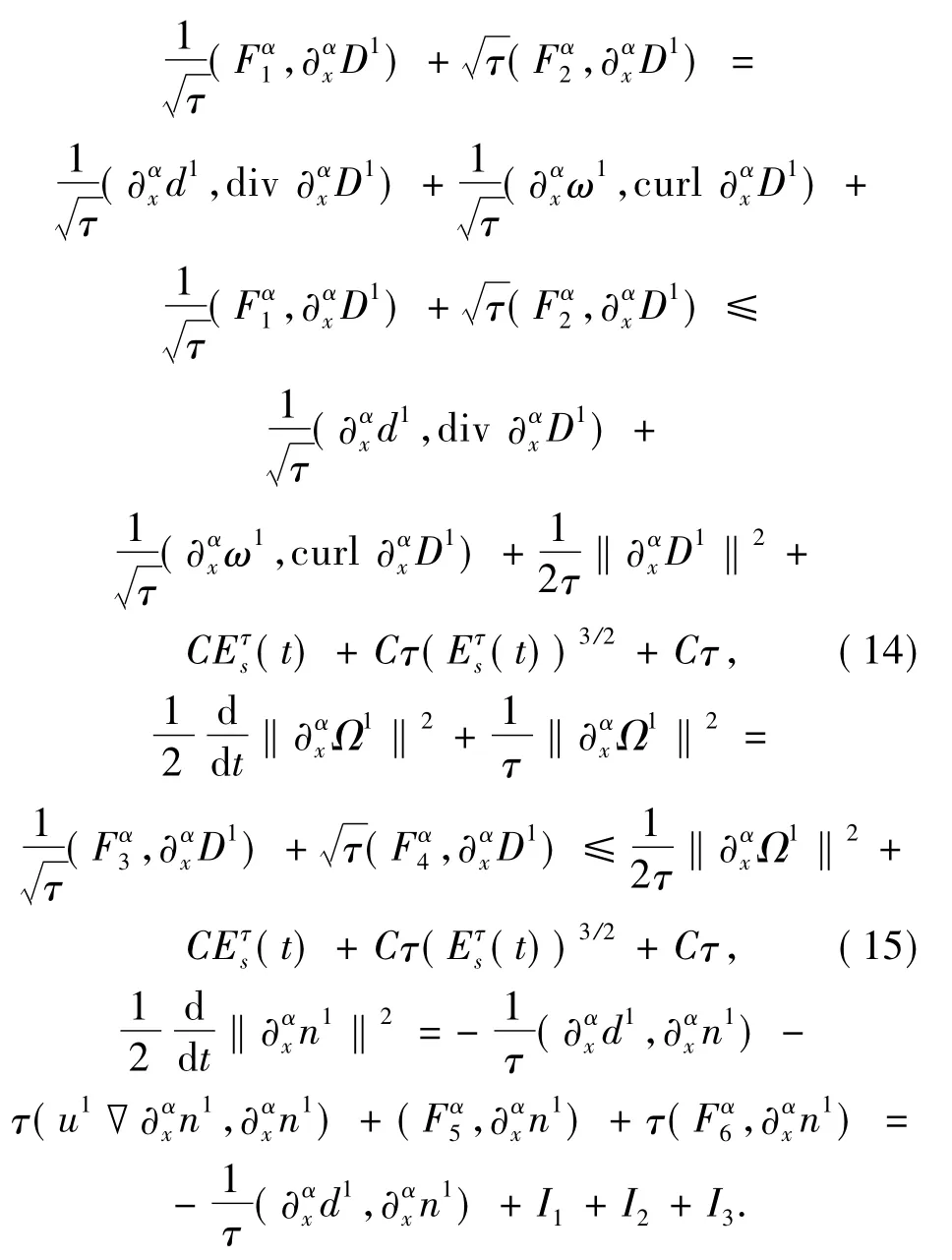
By an integration by parts，we have

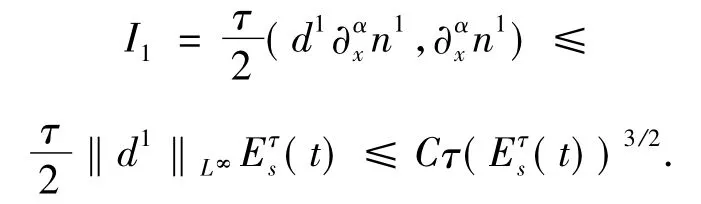
The termsI2andI3are easily estimated by

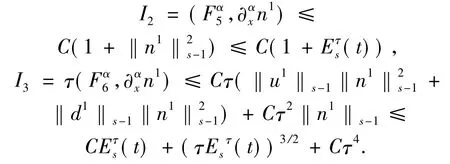
Therefore，we obtain the estimate

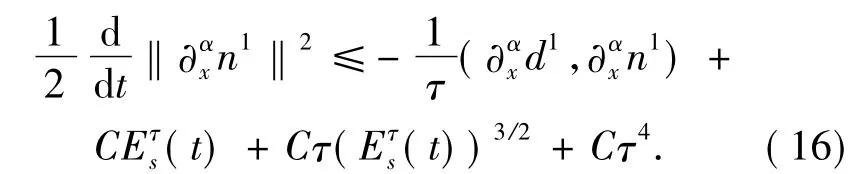
Combining(9)with(12)～(16)together and summing this over all multiindexes α≤s-1，one gets

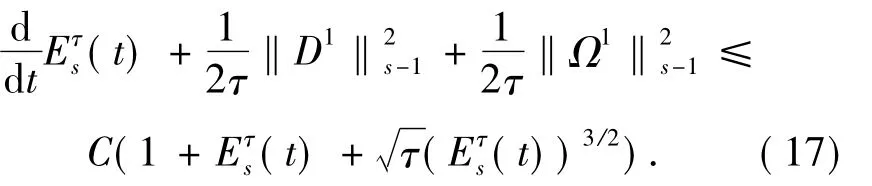
Then by the Gronwall inequality and the initial data assumption(6)we can conclude，that if the solution(u0，φ0)of incompressible Navier-Stokes equations(4)is smooth on the time interval［0，T］，for anyT1＜Tthere exists τ0such that the sequence(n1，d1，ω1，D1，Ω1) ‖τ＜τ0is bounded inC(［0，T］，Hs-1(T2)).Then we have

This proves Theorem 2.1.

AcknowledgmentsThe authors are very grateful to both referees for their constructive comments and helpful suggestions，which considerably improved the presentation of the paper.

［1］Bouchut F，Golse F，Pulvirenti M.Kinetic Equations and Asymptotic Theory［M］.Paris:Gauthiers-Villars，2000.

［2］Donatelli D，Marcati P.Convergence of singular limits for multi-D semilinear hyperbolic systems to parabolic systems［J］.Trans Am Math Soc，2004，356:2093-2121.

［3］Marcati P，Rubino B.Hyperbolic to parabolic relaxation theory for quasilinear first order systems［J］.J Diff Eqns，2000，162:359-399.

［4］Brenier Y，Natalini R，Puel M.On a relaxation approximation of the incompressible Navier-Stokes equations［J］.Proc Am Math Soc，2004，132:1021-1028.

［5］Jin S，Liu H L.Diffusion limit of a hyperbolic system with relaxation［J］.Meth Appl Anal，1998，5:317-334.

［6］Yong W A.Relaxation limit of multi-dimensional isentropic hydrodynamical models for semiconductors［J］.SIAM J Appl Math，2004，64:1737-1748.

［7］ Natalini R，Rousset F.Convergence of a singular Euler-Poisson approximation of the incompressible Navier-Stokes equations［J］.Proc Am Math Soc，2006，134:2251-2258.

［8］Xu J，Yong W A.Relaxation-time limits of non-isentropic hydrodynamic models for semiconductors［J］.J Diff Eqns，2009，247:1777-1795.

［9］Yang J W，Wang S.The diffusive relaxation limit of non-isentropic Euler-Maxwell equations for plasmas［J］.J Math Anal Appl，2011，380:343-353.

［10］廖為，蒲志林.一類擬線性橢圓型方程Dirichlet問題正解的存在性［J］.四川師范大學(xué)學(xué)報:自然科學(xué)版，2007，30(1):31-35.

［11］李傳華，馮春華.一類二階常p-Laplace系統(tǒng)周期解的存在性［J］.廣西師范大學(xué)學(xué)報:自然科學(xué)版，2011，29(3):28-32.

［12］McGrath F J.Nonstationary plane flow of viscous and ideal fluds［J］.Arch Rational Mech Anal，1968，27:229-348.

［13］Kato T.Nonstationary flow of viscous and ideal fluids in R3［J］.J Funct Anal，1972，9:296-305.

［14］Loeper G.Quasi-neutral limit of the Euler-Poisson and Euler-Monge-Ampère systems［J］.Commun Partial Diff Eqns，2005，30:1141-1167.

［15］Taylor M E.Partial Differential Equations(III)of Applied Mathematical Sciences［M］.New York:Springer-Verlag，1997.