基于一種新型轉子磁鏈觀測方法的矢量控制高壓變頻器

齊桓若， 劉其輝

(華北電力大學 電氣與電子工程學院輸配電所，北京 102206)

0 引 言

高壓變頻器的控制策略主要有VF控制和矢量控制。矢量控制是一種高效節能的電機調速方法，可實現異步電機的解耦控制，讓異步電機的調速擁有如同直流電機一般的優越性能。

矢量的定向準確與否在矢量控制的效果方面起到至關重要的作用。本文采用轉子磁鏈定向的矢量控制策略，則能否準確的觀測轉子磁鏈的位置角與幅值成為關鍵。本文除了比較了傳統磁鏈觀測器的優劣外，還提出一種新型轉子磁鏈觀測方法，并在此基礎上實現了異步電機的解耦控制。

1 級聯型高壓變頻器結構及移相載波SPWM

級聯型是串聯型高壓變頻器由多個獨立的低壓功率單元串聯提升輸出電壓，實現高壓輸出。該工作方式能保證在其中一個功率單元出現故障的時候其他功率單元不受影響，具有較高的可靠性。級聯型高壓變頻系統主要由移相變壓器、級聯功率單元和電機組成，級聯型變頻器拓撲結構圖如圖1所示。當高壓變頻器的額定輸出電壓為6 kV時，每一相由6個額定電壓為580 V的功率單元級聯，則可輸出相電壓3 480 V，線電壓6 kV。6單元級聯6 kV高壓變頻器簡圖如圖2所示。每個功率單元的拓撲結構如圖3所示。每個功率單元由一個三相不控整流環節將交流電整流為直流，再通過SPWM控制H橋逆變器4個橋臂IGBT管子的導通和關斷將直流電逆變為頻率和電壓符合要求的交流電。每個H橋逆變器工作在+Udc、-Udc、0三電平工作方式下，這樣經過移相6單元級聯可輸出13電平相電壓和25電平線電壓，使輸出的波形接近于正弦波。

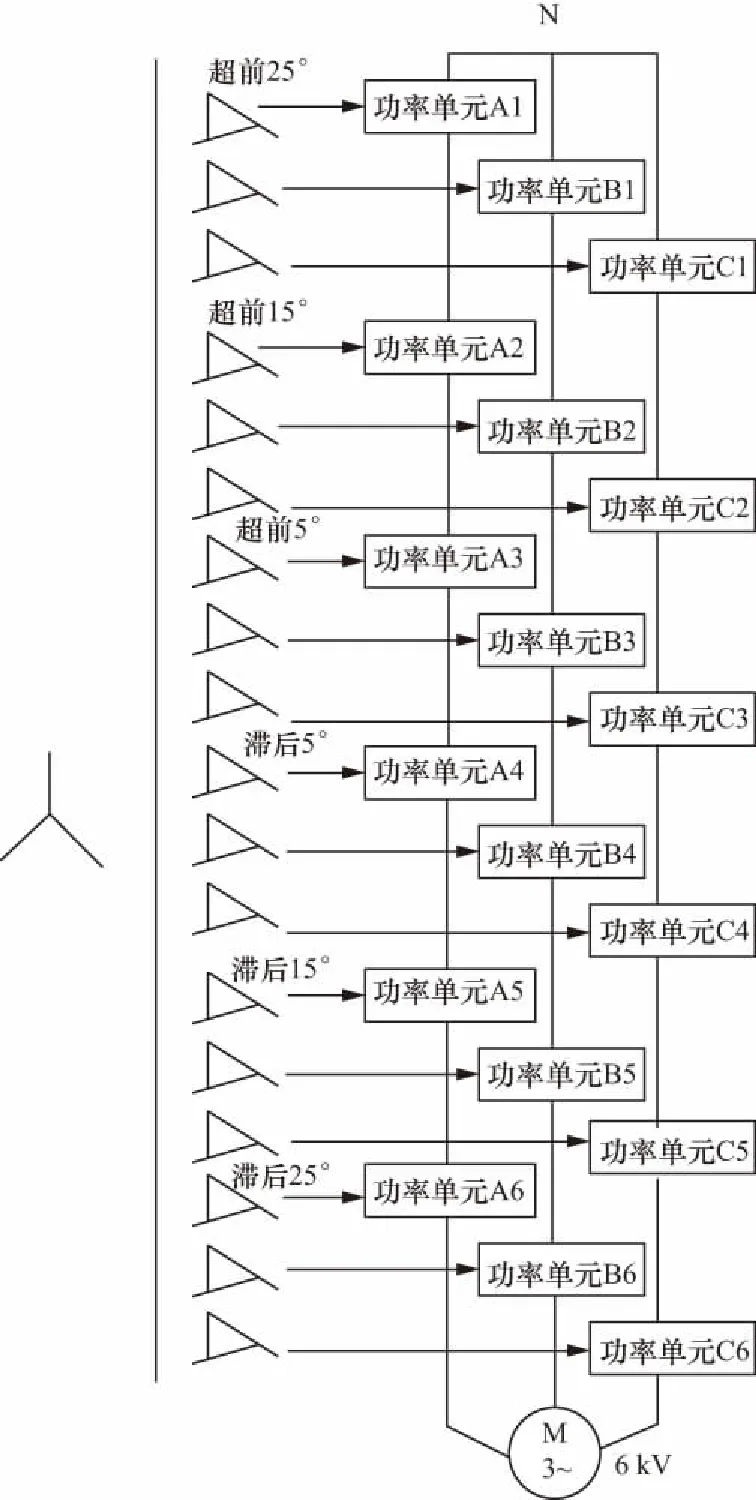
圖1 級聯型變頻器拓撲結構圖

圖2 6單元級聯6 kV高壓變頻器簡圖

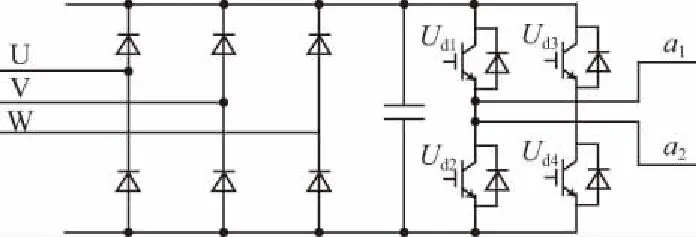
圖3 級聯功率單元拓撲結構

多電平載波移相法是指對于一個n電平變換器，n-1個不同相位的三角載波分別與同一個調制波進行比較，生成相對獨立的n-1組PWM調制信號，去驅動功率單元。對于6單元級聯的變頻器，由于每個功率單元需要兩組調制信號。Ud1與Ud2不能同時導通，否則會短路，因此Ud1與Ud2互補稱為一組，Ud3與Ud4互補稱為第二組。共要12組調制信號，各個載波依次移相360°/12即30°產生13電平相電壓信號。級聯變頻器輸出相電壓與調制波波形如圖4所示。其中Ua為變頻器輸出a相相電壓的波形，at為級聯單元的調制波。

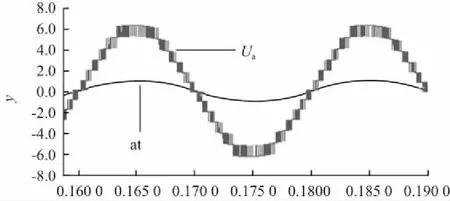
圖4 級聯變頻器輸出相電壓與調制波波形

從圖中可以看出，Ua為13電平近似于正弦波形，并且與調制波at相位相等，但幅值并不相等。原因是at為每個級聯單元的調制信號，而整個變頻器的單相有6個級聯單元相串聯。若將at擴大6倍即為整個變頻器的單相調制信號，與變頻器的輸出相電壓相位和幅值均一致。

2 異步電機動態數學模型

異步電動機在三相靜止坐標系下的模型是一個高階、非線性、強耦合的多變量系統。動態數學方程式，有八階，并且參數不恒定。基于磁動勢不變原則，可以通過坐標變換把異步電動機在三相靜止坐標系上的數學模型等效到兩相靜止坐標系中。由于兩相坐標軸互相垂直，兩相繞組之間沒有磁的耦合。利用這種恒等變換，可以簡化數學模型。異步電機在兩相靜止坐標系上的數學模型比在三相靜止坐標系上的要簡單的多，階次也降低了，但是其非線性、多變量、強耦合的性質并未改變。但如果對兩相繞組通以直流電，讓坐標系旋轉，構成兩相任意旋轉坐標系，再求出某一特定的兩相旋轉坐標系上的模型就較為簡易。

兩相同步旋轉坐標系上，用定子電流和轉子磁鏈表示的電壓方程為

(1)

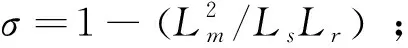
U——電壓；

I——電流；

R——電阻；

L——電感；

P——微分符號；

J——轉動慣；

Ω——角速度；

S、r——定子和轉子；

ω1——同步角速度；

ωs——轉差角速度。

轉矩方程為

(2)

3 轉子磁場定向的矢量控制系統原理

在兩相同步旋轉坐標系的建立過程中，規定了d、q兩軸互相垂直，且與定子頻率同步旋轉，并未規定兩軸與電機旋轉磁場的相對位置。如果取d軸沿著轉子磁鏈ψr同步同方向旋轉，而q軸與轉子磁鏈垂直，此時應有

ψrd=|ψr|,ψrq=0

(3)

兩相同步旋轉坐標系就規定為按轉子磁鏈定向的旋轉坐標系。

將式(3)代入轉矩方程式(1)和式(2)，可得電磁轉矩和電壓方程分別為

(4)

(5)

由式(5)第4行可得

(6)

由式(5)第3行可得

(7)

以上式(4)～式(7)和運動方程式(8)組成了d、q坐標系上異步電機的數學模型，如圖5所示。

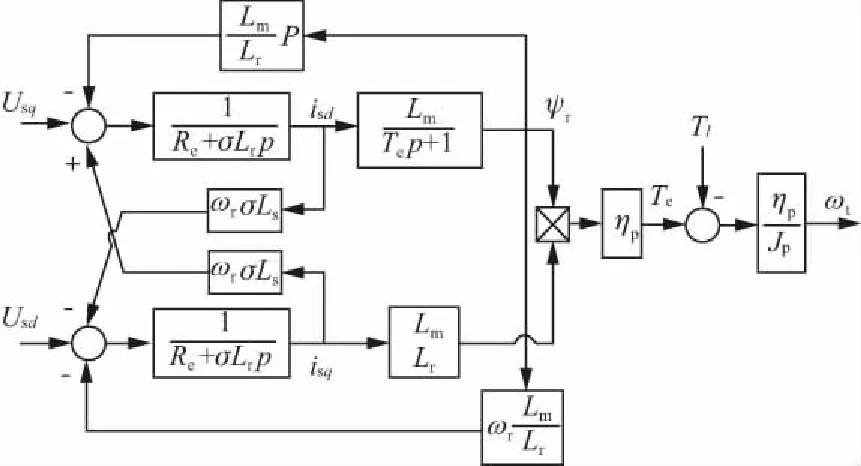
圖5 d、q坐標系上感應電機的模型

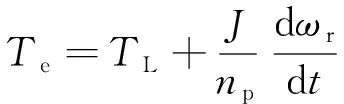
(8)

由圖5可得，轉子磁鏈Ψr由定子電流勵磁分量isd產生，兩者之間為一階慣性環節關系，體現了建立磁場的勵磁過程。轉子磁鏈與轉矩分量isq無關，如果除去耦合項ω1σLs的影響，isd和isq可以視之為解耦。系統設計時可以將ω1σLs看作擾動，給與前饋補償處理。這樣電機可以分為兩個獨立的子系統：(1)由電壓分量usd為輸入，定子電流的勵磁分量isd決定的勵磁子系統。該分支決定了電機工作在額定勵磁值附近，可以輸出最大的電磁轉矩。(2)由電壓分量usq為輸入，定子電流的轉矩分量isq為輸出的轉矩子系統，isq與電磁轉矩Te成線性關系。

由于電磁轉矩Te=np(Lm/Lr)isqΨr，Te同時受isq和Ψr影響，依然是耦合的。但轉子磁鏈定向的成立條件是Ψrd=|Ψr|和Ψrq=0，在Ψrd=|Ψr|=Const的條件下，Te與isq為線性關系，由此，對轉矩的控制就轉變成對轉矩電流的控制問題。

矢量控制結構框圖如圖6所示。

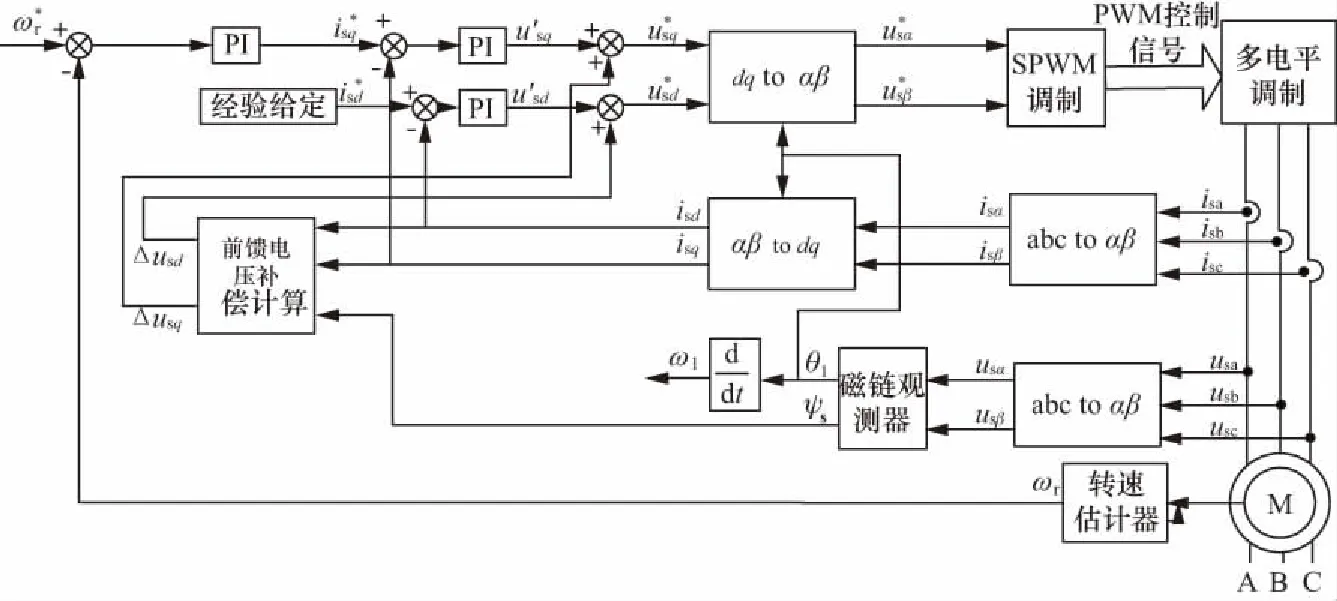
圖6 轉子磁鏈定向矢量控制結構框圖

4 傳統轉子磁鏈觀測模型

4.1 基于兩相靜止坐標系上的電流模型

兩相靜止坐標系上轉子磁鏈的電流模型為

(9)

兩相靜止坐標系上轉子磁鏈觀測電流模型如圖7所示。

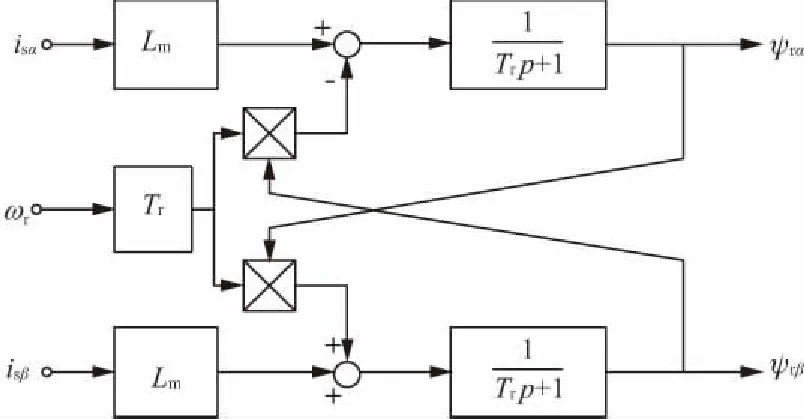
圖7 兩相靜止坐標系上轉子磁鏈觀測電流模型

從圖7中可以看出，轉子磁鏈的電流模型需要實測的定子電流和轉速信號，不論轉速高低都適用，但是都受電機參數變化的影響嚴重。例如電機溫升效應引起的轉子電阻的變化。

4.2 電壓模型

轉子磁鏈的電壓模型為

(10)

轉子磁鏈電壓模型如圖8所示。由圖可知，只需實測的定子電壓和電流信號，無需轉速信號，且算法與轉子電阻Rr無關，只與定子電阻有關Rs有關。Rs是容易測得的。與電流模型相比，電壓模型受電機參數變化的影響小、算法簡單。但電壓模型中包含純積分項，直流偏置會導致計算出的磁鏈有累積誤差，且在低速時，定子電阻壓降變化的影響較大，使電壓模型不夠準確。

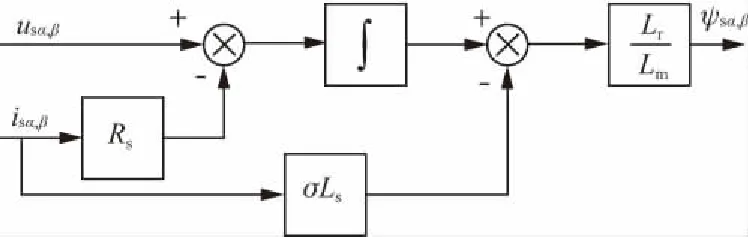
圖8 計算轉子磁鏈的電壓模型

4.3 勵磁電流補償的改進電壓模型[10]

轉子磁鏈狀態估計的動態方程為

(11)

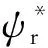
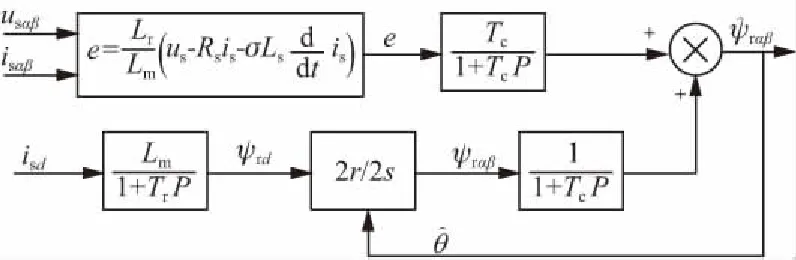
圖9 勵磁電流補償的改進電壓模型框圖

勵磁電流補償的改進電壓模型如圖9所示。該模型是電流模型與電壓模型的組合，兼具兩者優點。在低速時能避免電壓模型定子電阻壓降的影響，在高速時能避免電流模型電機參數變化的影響，且此模型不需要轉子轉速的實測信號。

4.4 轉子磁鏈檢測模型的仿真結果

為了比較三種磁鏈觀測的優劣，分別仿真了在低轉速和高轉速指令下的情況。

4.4.1 低轉速下的仿真

恒定勵磁；轉速指令為45 rad/s(約0.14 pu)；負載模擬了風機水泵類流體負載Tload=kωr2+b。

圖10為低速時三種磁鏈觀測器觀測到的轉子磁鏈值。圖11為低速時三種磁鏈觀測器觀測到的轉子磁鏈位置角放大圖。feir、thetar為電流模型的觀測值，feir2、thetar2為電壓模型的觀測值，feir3、thetar3為勵磁電流補償的改進電壓法的觀測值。

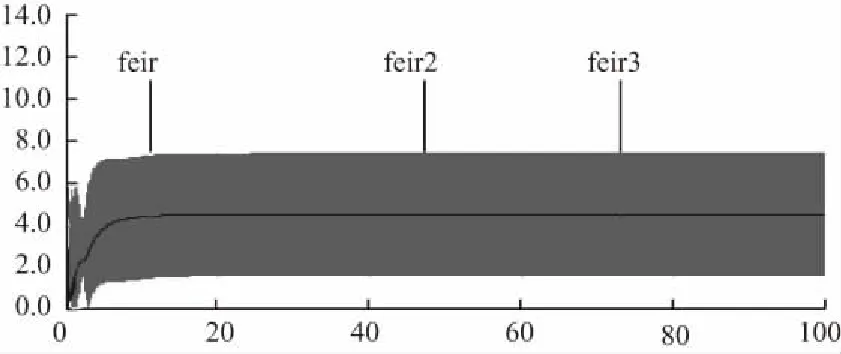
圖10 低速時三種磁鏈觀測器觀測到的轉子磁鏈值

圖中feir曲線與feir3曲線完全重合。

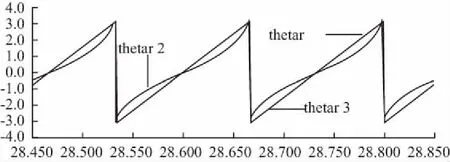
圖11 低速時三種磁鏈觀測器觀測到的轉子磁鏈位置角放大圖

圖中thetar曲線與thetar3曲線完全重合。

從圖10、圖11中可知，在低速時轉子電流模型和勵磁電流補償的改進電壓模型都能準確的觀測轉子磁鏈。電壓模型觀測出的磁鏈值是震蕩的，位置角存在一定程度的畸變，有可能使轉速無法跟蹤。出現位置角畸變和幅值不準是因為積分環節產生的直流偏置問題。兩相靜止坐標系下電流模型與電壓模型轉子磁鏈觀測放大圖如圖12所示。其中曲線ralfa是電流模型觀測到的值，ralfa2是電壓模型觀測到的值。可以看出，ralfa2的中心線明顯偏離了橫坐標0軸，出現了直流偏置。這也是出現圖10中磁鏈觀測震蕩的主要原因。

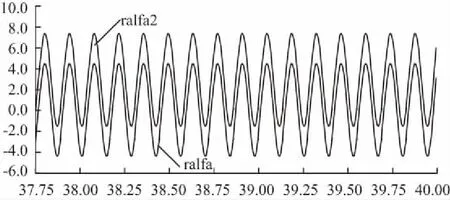
圖12 兩相靜止坐標系下轉子磁鏈觀測值放大圖

4.4.2 高轉速下的仿真

采用恒定勵磁；轉速指令為310 rad/s(約0.98 pu)；負載依然模擬了風機水泵類流體負載Tload=kωr2+b。

高速運行時，電機的溫升會使轉子電阻變大。這是影響轉子磁鏈觀測準確性的重要因素之一。嚴重時對轉子電阻的影響有可能超過50%。以50%為例來研究轉子電阻變化對三種磁鏈觀測的影響。選取兩相靜止坐標系電流模型觀測的feir0、thetar0作為標準參考。將電流、電壓、改進電壓模型中的轉子電阻增大50%，從0.182 6 Ω變為0.273 9 Ω，轉子時間常數Tr從2.506 6 s變為1.671 s，以此來模擬高轉速運行帶來的溫升效應。電機模型中實際轉子電阻保持0.182 6 Ω不變。

磁鏈觀測模型轉子電阻變化50%時三種磁鏈觀測器觀測到的轉子磁鏈值如圖13所示，磁鏈觀測模型轉子電阻變化50%三種磁鏈觀測器觀測到的轉子位置角如圖14所示。其中feir0、thetar0為標準參考值，feir、thetar為電流模型的觀測值，feir2、thetar2為電壓模型的觀測值，feir3、thetar3為勵磁電流補償的改進電壓法的觀測值。

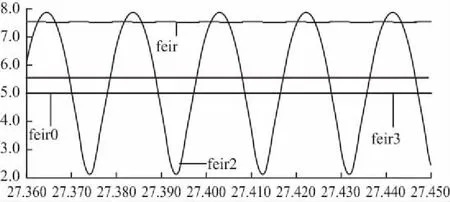
圖13 磁鏈模型轉子電阻變化50%時三種磁鏈觀測器觀測到的轉子磁鏈值放大圖

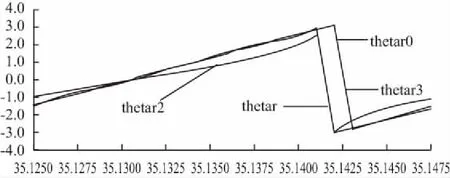
圖14 磁鏈模型轉子電阻變化50%三種磁鏈觀測器觀測到的轉子位置角放大圖

從圖13、圖14中可知，溫升帶來的轉子電阻升高導致電流模型的轉子磁鏈觀測值比實際值大了很多，觀測的轉子磁鏈位置角也超前于實際位置。電壓模型的觀測值在實際值附近震蕩，并且觀測的轉子位置角也有一定程度的畸變，依然存在直流偏置問題。勵磁電流補償的改進電壓法觀測的磁鏈雖然也大于實際值，但比電流模型的誤差小得多，觀測的位置角與實際位置角基本一致，高速時溫升效應引起的轉子電阻變化對此模型的影響較電流模型來說被顯著削弱了。

綜上所述，勵磁電流補償的改進電壓法結合了電流法與電壓法的優點。無論在高轉速亦或是低轉速下都實現轉子磁鏈較為準確的觀測，且結構簡單，無需對轉子轉速進行檢測，實現容易，是一種良好的轉子磁鏈觀測模型。

5 一種新型轉子磁鏈觀測器

雖然勵磁電流補償的改進電壓法有很多優點，但是參數估計不準還是會給觀測帶來誤差。另外，模型中的時間常數Tc如果設置不合適，也會引起轉子磁鏈觀測幅值的偏差。具體表現為：若Tc過大，會引起磁鏈動態觀測過程的小幅震蕩與觀測值略低于實際值；若Tc過小則會引起觀測值略高于實際值。

本文提出一種轉子磁鏈觀測器，在勵磁電流補償的電壓模型基礎上，引入非線性正交補償。

新型轉子磁鏈觀測器觀測到的磁鏈表達式為

ψr=ψV+ψx

(12)

式中：Ψr——新型轉子磁鏈觀測器的觀測值；

ΨV——勵磁電流補償的改進電壓模型的觀測值；

Ψx——磁鏈反饋補償信號。

若磁鏈觀測準確，則Ψx為0。若觀測不準確，需要根據實際誤差大小來動態確定補償系數。補償信號Ψx的表達式為

ψx=λψr

(13)

補償系數λ取決于觀測的磁鏈矢量與檢測的反電勢矢量之間的正交程度，由式(14)決定

(14)

由于磁鏈與反電動勢呈積分關系，如果觀測準確，則兩矢量必然正交，補償系數應為0。如果二者不正交，則λ可以反映誤差的大小，進而確定補償量來修正觀測值，直到觀測準確。

高轉速下用新型磁鏈觀測器觀測到的轉子磁鏈值與轉子磁鏈位置角如圖15所示。其中feir4、thetar4為新型觀測器的觀測值，feir0、thetar0為參考值。由圖可知，兩者幾乎完全重合。說明新型磁鏈觀測器具有很高的準確性與實用性。

圖15 新型磁鏈觀測器觀測到的轉子磁鏈值與轉子磁鏈位置角

6 基于新型轉子磁鏈觀測方法的異步電機矢量控制仿真結果與結論

采用新型轉子磁鏈觀測方法來進行磁鏈觀測。仿真條件為：采用恒定勵磁；轉速指令從0開始逐漸增至300 rad/s，后在60 s時刻從300躍變至180 rad/s；負載轉矩模擬了風機水泵類流體負載Tload=kωr2+b。

轉速指令Wf與實際轉速WF波形如圖16所示。負載轉矩Tload與電磁轉矩Te波形如圖17所示。新型轉子磁鏈觀測器觀測到的轉子磁鏈值feir4如圖18所示。定子q軸電流指令值isqref與實際值isq波形如圖19所示。定子d軸電流指令值isdref與實際值isd波形如圖20所示。

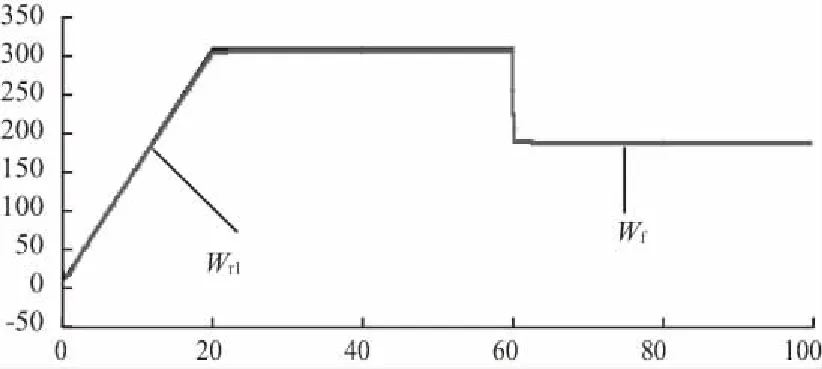
圖16 轉速指令Wf與實際轉速WF波形

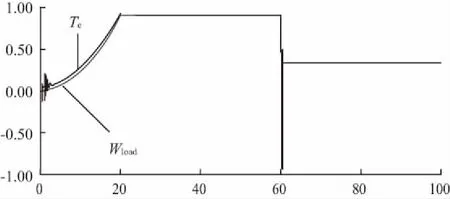
圖17 負載轉矩Tload與電磁轉矩Te波形

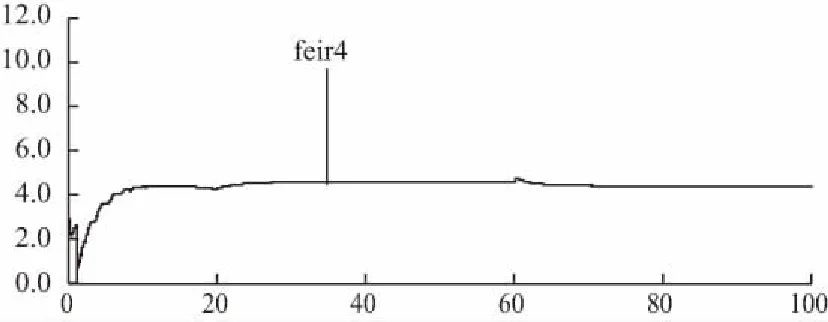
圖18 新型轉子磁鏈觀測器觀測到的轉子磁鏈值feir4

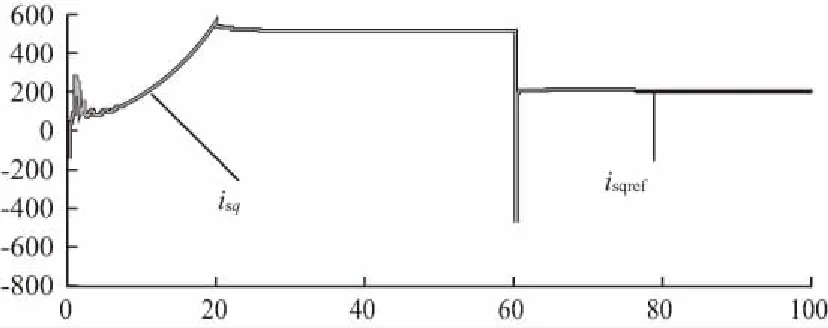
圖19 定子q軸電流指令值isqref與實際值isq

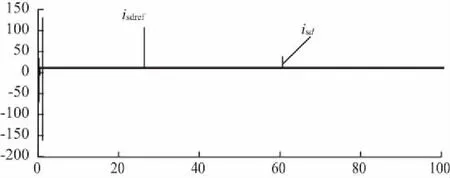
圖20 定子d軸電流指令值isdref與實際值isd

由圖可知，轉子轉速、定子電流d軸分量與q軸分量都分別良好地跟蹤了指令值；定子電流d軸分量與q軸分量互不影響；轉子磁鏈與轉子轉速也基本互不影響，真正實現了勵磁與轉速的解耦控制。滿足電機高性能調速的要求。

異步電機定子線電壓波形圖如圖21所示。異步電機定子線電流波形圖如圖22所示。

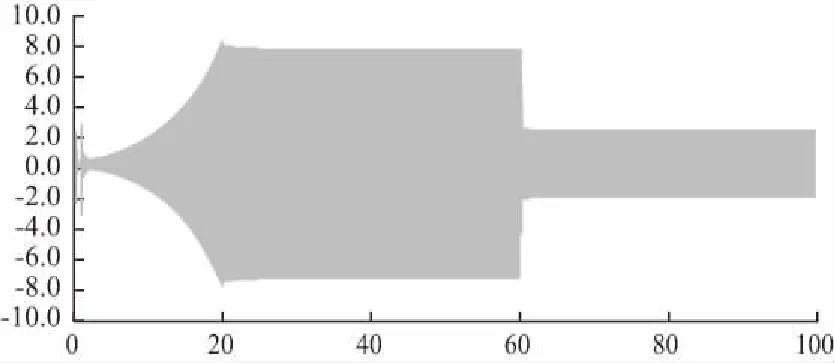
圖21 異步電機定子線電壓波形圖

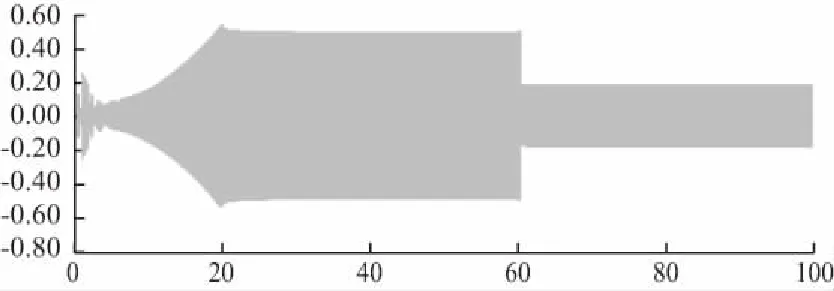
圖22 異步電機定子線電流波形圖

[1] 王會濤,錢希森,王吉校,等.轉差頻率控制的異步電動機矢量控制調速系統的研究和仿真[J].電氣應用，2007(11)：80-83.

[2] 何萍,郭軍.基于MATLAB/Simulink的異步電機直接轉矩控制系統仿真[J].電氣應用，2007(1)：84-87.

[3] 李永東，肖曦，高躍.大容量多電平變換器：原理 控制 應用[M].北京：科學出版社，2005.

[4] 劉鳳君.多電平逆變技術及應用[M].北京：機械工業出版社，2007.

[5] 南永輝, 羅仁俊, 伍海林.基于級聯型多電平高壓變頻器的異步電機控制策略[J]. 變流技術與電力牽引，2008(5)：11-15.

[6] 馬志云.電機瞬態分析[M].北京：中國電力出版社,1998.

[7] 張立偉,溫旭輝, 陳桂蘭. MATLAB/Simulink環境下異步電機建模及其工程應用[J].電氣應用，2006(4)：119-122.

[8] 柳黎明.基于矢量控制的異步電機轉速和轉矩調節技術[J].機電工程，2011(4)：504-508.

[9] 陳伯時.電力拖動自動控制系統[M].北京：機械工業出版社，1992.

[10] 李光.10kV單元串聯式高壓變頻器及其矢量控制策略的研究[D].上海:東華大學,2008.