用于三維非均質(zhì)流場計(jì)算的改進(jìn)流線迎風(fēng)Petrov-Galerkin(SUPG)方法

蘇波,韓向科

(1.江蘇大學(xué)土木工程與力學(xué)學(xué)院, 212013, 江蘇鎮(zhèn)江; 2.中冶天工上海十三冶建設(shè)有限公司, 200092, 上海)

用于三維非均質(zhì)流場計(jì)算的改進(jìn)流線迎風(fēng)Petrov-Galerkin(SUPG)方法

蘇波1,韓向科2

(1.江蘇大學(xué)土木工程與力學(xué)學(xué)院, 212013, 江蘇鎮(zhèn)江; 2.中冶天工上海十三冶建設(shè)有限公司, 200092, 上海)

在流線迎風(fēng)Petrov-Galerkin(SUPG)穩(wěn)定有限元方法基礎(chǔ)上,通過引入雙時間步法和變量分裂算法,發(fā)展了一種可用于三維非均質(zhì)流場計(jì)算的改進(jìn)SUPG方法。該方法摒棄了傳統(tǒng)不可壓縮流動問題中密度為常數(shù)的假定,采用包含密度輸運(yùn)方程的流體運(yùn)動控制方程;基于變量分裂算法,速度、壓強(qiáng)場采用同階插值函數(shù)進(jìn)行空間離散,使改進(jìn)SUPG方法具有簡明的有限元格式,同時對速度場、壓強(qiáng)場進(jìn)行迭代求解,以降低線性代數(shù)方程組的階數(shù)。雙時間步法的引入,有利于提高SUPG方法對復(fù)雜非定常問題的求解效率。采用該方法對非均質(zhì)、非定常三維矩形管道重力作用下的自由流動問題進(jìn)行了分析,研究了重力作用下兩種不同密度液體的相對運(yùn)動過程。計(jì)算分析表明:在采用較大時間步的情況下,速度場和壓強(qiáng)場在整個流動過程中隨時間平穩(wěn)過渡且分布光滑,沒有出現(xiàn)數(shù)值波動現(xiàn)象;旋渦位置及其隨時間變化的規(guī)律與經(jīng)典文獻(xiàn)結(jié)果相符,沒有出現(xiàn)跳躍和不連續(xù)現(xiàn)象。算例分析表明,改進(jìn)SUPG方法具有良好的計(jì)算精度及數(shù)值穩(wěn)定性,可用于三維非均質(zhì)流動類似問題的研究。

不可壓流動;有限元法;分裂算法;流線迎風(fēng)

有限元方法由于可采用非結(jié)構(gòu)網(wǎng)格、易處理復(fù)雜邊界條件等優(yōu)點(diǎn),近些年來在工程問題中的流體計(jì)算領(lǐng)域得到了廣泛研究和重視[1-5]。但是,當(dāng)對流項(xiàng)占優(yōu)時,采用經(jīng)典Garlerkin法求解流體N-S方程會引起數(shù)值波動。Brooks和Hughes針對定常對流擴(kuò)散問題,提出了流線迎風(fēng)Petrov-Galerkin(SUPG)方法,有效地解決了對流項(xiàng)引起的數(shù)值波動問題[6]。Jameson提出了雙時間步法,在計(jì)算精度和計(jì)算效率上具有較高的優(yōu)越性,適合定常、非定常問題的求解[7]。此外,對于黏性不可壓流動問題,通過變量分裂法[8]將速度場和壓強(qiáng)場解耦,直接避免了LBB(Ladyzhenskaya-Babǔska-Brezzi)條件的限制,可以使單元速度、壓強(qiáng)采用同階插值函數(shù),易于對混合場進(jìn)行有限元空間離散。

在對黏性不可壓流動問題進(jìn)行有限元求解時,通常假定密度為常數(shù)[2,9],即采用均質(zhì)流場進(jìn)行求解。這樣雖然簡化了黏性不可壓流動問題的計(jì)算過程,但同時給問題的分析帶來局限性。為能對非均質(zhì)流場進(jìn)行精確分析,本文摒棄了密度為常數(shù)的假定,采用原始黏性不可壓流體運(yùn)動控制方程,繼而綜合運(yùn)用上述各種數(shù)值方法,提出一種適用于非定常黏性不可壓流動問題求解的改進(jìn)SUPG有限元方法,并給出相應(yīng)的有限元計(jì)算步驟和格式。最后,對三維管道中變密度液體在重力作用下的自由流動問題進(jìn)行分析,以驗(yàn)證該方法的有效性。

1 不可壓流體運(yùn)動控制方程

一般流體運(yùn)動的連續(xù)性方程為

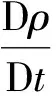
(1)

對于黏性不可壓流體,根據(jù)定義,流體的密度ρ在運(yùn)動過程中保持不變,即

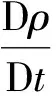
(2)

當(dāng)假定密度ρ為常數(shù)時,式(2)自動滿足,質(zhì)量守恒僅需滿足速度散度為0的條件。但是,對于非均勻流場,式(2)中隱含了密度場運(yùn)動條件,是不可忽略的,因此,對于非均質(zhì)黏性不可壓流體,其運(yùn)動控制方程為

(3)

(4)

(5)

式中:ρ為流體密度;Vi為流體速度分量;xi為直角坐標(biāo)分量;t為時間。式(3)、式(5)可簡寫為

(6)

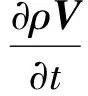
(7)

式中

2 控制方程的雙時間步離散

對式(6)、式(7)采用雙時間步法[7]進(jìn)行求解

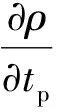
(8)

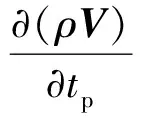
(9)

對式(8)、式(9)中關(guān)于虛擬時間tp的導(dǎo)數(shù)項(xiàng)采用加權(quán)隱格式[10]進(jìn)行時間離散,關(guān)于物理時間的導(dǎo)數(shù)項(xiàng)采用二階精度三點(diǎn)向后差分格式,得

(10)

(11)

式中

(12)

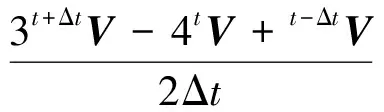
(13)

上角標(biāo)t表示物理時刻t的已知變量;tp表示虛擬時刻tp的已知變量;t+Δt表示物理時刻t+Δt的待求變量;tp+Δtp表示虛擬時刻tp+Δtp的待求變量;Δt為物理時間步長;Δtp為虛擬時間步長;tp+ΔtpΔρ為虛擬時間的密度增量,tp+ΔtpΔρ=tp+Δtpρ-tpρ;tp+ΔtpΔV為虛擬時間的速度增量,tp+ΔtpΔV=tp+ΔtpV-tpV;θρ、θV、θp為時間離散權(quán)系數(shù)。

3 求解流體運(yùn)動控制方程的變量分裂法

采用變量分裂算法[8],對式(10)、式(11)方程組的速度場、壓強(qiáng)場進(jìn)行迭代求解,計(jì)算步驟如下:

第1步,由式(10)求出時刻tp+Δtp的密度增量tp+ΔtpΔρ及密度全量tp+Δtpρ=tpρ+tp+ΔtpΔρ;

第2步,不考慮壓強(qiáng)項(xiàng)及ΔVi,r項(xiàng),計(jì)算中間速度增量

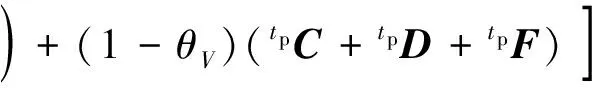
(14)

第3步,將中間速度增量tp+ΔtpΔVint及密度全量tp+Δtpρ代入下式,求解壓強(qiáng)tp+Δtpp

(15)

第4步,根據(jù)tp+ΔtpΔVint和tp+θpΔtpp,求解速度增量

tp+ΔtpΔV=tp+ΔtpΔVint-

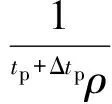
(16)

式(10)、式(14)～(16)即構(gòu)成了基于變量分裂方法的非定常不可壓流體運(yùn)動的基本方程。當(dāng)流場為均質(zhì)流體,即密度不隨空間改變時,連續(xù)性方程(3)自動滿足,則上述方法退化為一般不可壓流動分裂算法。

4 基于SUPG方法的不可壓流動穩(wěn)定有限元格式

對式(10)采用SUPG方法[1,6]進(jìn)行空間離散,得到連續(xù)性方程的有限元格式

mρtp+ΔtpΔρe=rρ

(17)

式中

(18)

對式(14)采用SUPG有限元格式進(jìn)行空間離散,得到輔助動量方程有限元格式

(19)

式中

(20)

方程組(15)可簡寫為泊松型壓強(qiáng)方程[11],采用標(biāo)準(zhǔn)Galerkin有限元格式離散,得到計(jì)算壓強(qiáng)的有限元格式的弱形式

Δtphtp+ΔtpΔpe=rp

(21)

式中

(22)

rp=θp(tp+Δtpgp-Δtphtp+Δtppe-tp+Δtpfρ)+

(1-θp)(tpgp-Δtphtppe-tpfρ)

(23)

其中

對速度修正方程,式(16)采用標(biāo)準(zhǔn)Galerkin有限元格式離散,有限元格式為

(24)

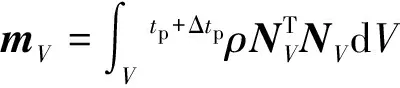
(25)

式(17)、(19)、(21)、(24)即構(gòu)成了可用于非均質(zhì)流場計(jì)算的改進(jìn)SUPG穩(wěn)定有限元格式。

5 非均質(zhì)、非定常三維矩形管道重力作用下的自由流動問題

5.1 計(jì)算模型

在非均質(zhì)流動算例中,雙層流體在重力作用下的自由流動問題[12]是一個十分典型的算例。如圖1所示,有一矩形流場,流場內(nèi)盛有2種不同密度的流體,密度分別為ρ1和ρ2,且ρ2>ρ1,密度較大的流體位于流場上部,密度較小的流體位于流場下部。參考二維算例[13],初始密度分布為

ρ(x,y,z,t=0)=

(26)

式中:η(x)=-0.1dcos(2πx/d);d為指定長度。

(a)流場幾何尺寸 (b)有限元網(wǎng)格劃分

有限元網(wǎng)格劃分形式見圖1b,計(jì)算雷諾數(shù)定義為Re=ρ1d3/2g1/2/μ[14],其中g(shù)為重力加速度,μ為液體的動力黏性系數(shù)。其他計(jì)算條件見表1。

表1 雙層液體流動模型計(jì)算條件

在重力作用下,流場中2種液體發(fā)生相對運(yùn)動。雖然流場形狀簡單,但隨著上部液體向下流動,2種液體逐漸融合交織,導(dǎo)致流動狀態(tài)十分復(fù)雜,流動對網(wǎng)格形式、邊界條件等因素十分敏感,容易引起數(shù)值求解失敗[13]。

5.2 結(jié)果分析

圖2給出了流場在不同時刻的密度分布規(guī)律。在重力作用下,矩形流場上部密度較大的液體向下流動。當(dāng)t=1 s時,2種液體分界面逐漸擴(kuò)大,但流場分布規(guī)律仍和初始分布規(guī)律基本相似;當(dāng)t=1.5s時,上部液體繼續(xù)向下流動,且在兩液體交界面處開始形成旋渦,但2種液體仍然具有較為明顯的分界面;當(dāng)t=1.75s時,與t=1.5s時的分布規(guī)律基本一致,2種液體交界面處旋渦更加明顯;當(dāng)t=2 s時,2種液體的交界面逐漸擴(kuò)大,并相互交織,旋渦繼續(xù)增強(qiáng),旋渦中心逐漸上移;當(dāng)t>2 s時,流場的流動特性開始發(fā)生改變,隨著2種液體的交界面繼續(xù)擴(kuò)大,交界面逐漸模糊,流場中部2種液體已相互滲透,流動情況愈加復(fù)雜,這與文獻(xiàn)[13-14]中給出的分布規(guī)律相同。

圖3～圖5給出了整個流動過程中的壓強(qiáng)和速度場分布規(guī)律。如圖所示,在整個時段內(nèi),盡管流動狀態(tài)復(fù)雜,但壓強(qiáng)和速度分布光滑,隨時間變化過渡平穩(wěn),可以得到穩(wěn)定的壓強(qiáng)場和速度場,沒有出現(xiàn)數(shù)值波動現(xiàn)象。

圖6和圖7分別給出了流動過程中的流線圖和流場中旋渦位置隨時間的變化規(guī)律。在整個流動過程中,旋渦位置在x方向變化幅度較小,在約t=1 s之前旋渦略向左側(cè)靠攏,隨后逐漸向右側(cè)邊發(fā)展;相比之下,旋渦位置在z方向變化幅度較為明顯,在t=0.5s之前z向坐標(biāo)值變化較為緩慢,隨后迅速變小,至約1.8 s左右又逐漸增大,整體呈正弦曲線規(guī)律。圖8給出了流場的上部和下部液體分界面位置隨時間的變化規(guī)律,可以看出,本文的計(jì)算結(jié)果與文獻(xiàn)[14]給出的計(jì)算結(jié)果十分吻合。

為使求解收斂,文獻(xiàn)[14]采用的歸一化時間步為Δtnon=5×10-4,文獻(xiàn)[15]選擇的歸一化時間步為Δtnon=0.001 25(At)1/2=8.84×10-4,而本算例采用較大的歸一化時間步:Δtnon=t(At)1/2=0.1(At)1/2=7.07×10-2。計(jì)算表明,在整個流動過程中旋渦位置變化平穩(wěn),沒有出現(xiàn)任何跳躍和不連續(xù)現(xiàn)象,依然可以獲得良好的計(jì)算精度,可見本文提出的改進(jìn)SUPG方法在時間方向具有良好的穩(wěn)定性能。

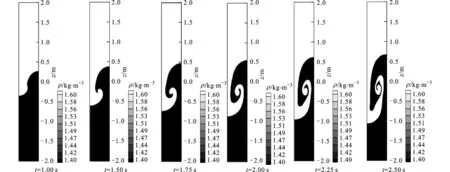
圖2 密度ρ的分布規(guī)律

圖3 速度Vx的分布規(guī)律

圖4 速度Vz分布規(guī)律

圖5 壓強(qiáng)p的分布規(guī)律

圖6 y=0.05m中面流線圖

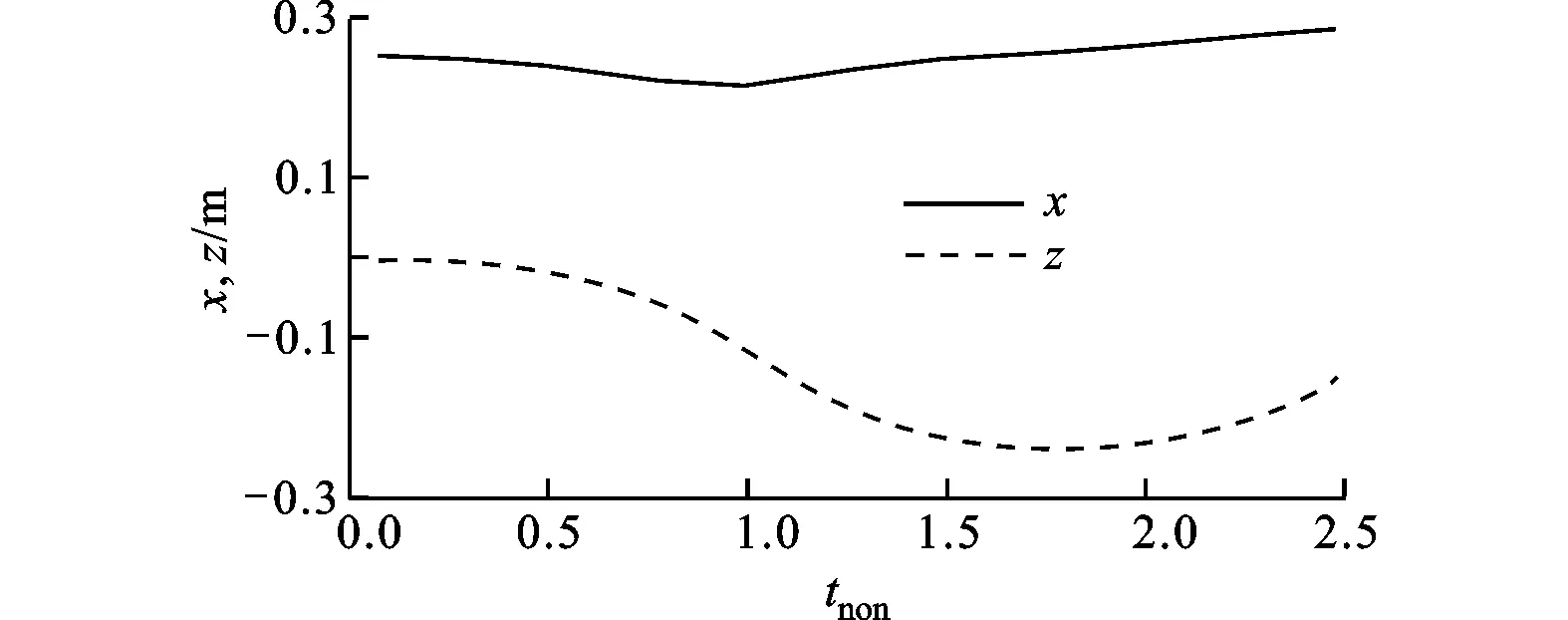
圖7 旋渦位置隨時間的變化

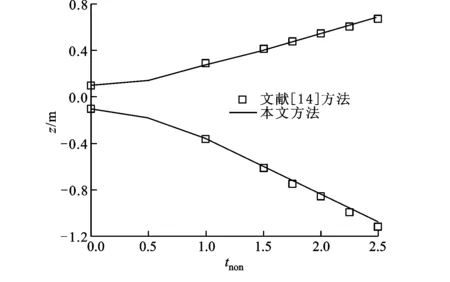
圖8 分界面位置隨時間的變化對比

6 結(jié) 論

本文所提出的改進(jìn)SUPG方法摒棄了密度為常數(shù)的假定,采用包含密度輸運(yùn)方程的黏性不可壓流體運(yùn)動控制方程組,使之可用于非均質(zhì)流場的分析。由于采用變量分裂算法,速度場和壓強(qiáng)場可采用同階插值函數(shù)進(jìn)行空間離散,使改進(jìn)SUPG方法具有簡明的有限元格式,并且速度場與壓強(qiáng)場可依次求解,降低了線性代數(shù)方程組的階數(shù),有利于大規(guī)模問題的求解。改進(jìn)SUPG方法引入雙時間步法進(jìn)行時間離散,有利于提高非定常問題的求解精度。算例分析表明,改進(jìn)SUPG方法可對重力作用下三維矩形管道內(nèi)的自由流動問題進(jìn)行有效分析,得到穩(wěn)定的速度場、壓強(qiáng)場以及渦流變化規(guī)律,從而實(shí)現(xiàn)對非均勻、非定常等復(fù)雜流動問題的求解。

[1] HUANG Cheng, ZHOU Dai, BAO Yan, et al.A stabilized finite element technique and its application for turbulent flow with high Reynolds number [J].Wind and Structures, 2011, 14(5): 465-480.

[2] ZIENKIEWICZ O C, TAYLOR R L.The finite element method for fluid dynamics [M].5th ed.Amsterdam, The Netherlands: Elsevier, 2000.

[3] 錢若軍, 董石麟, 袁行飛.流固耦合理論研究進(jìn)展 [J].空間結(jié)構(gòu), 2008, 4(1): 3-15.QIAN Ruo-jun, DONG Shi-lin, YUAN Xing-fei.Advances in research on fluid-structure interaction theory [J].Spacial Structures, 2008, 4(1): 3-15.

[4] 韓向科, 蘇波.黏性不可壓流體的一種FCBIS三角形單元 [J].力學(xué)與實(shí)踐, 2010, 32(3): 22-25.HAN Xiangke, SU Bo.A FCBIS triangular element for incompressible fluid flows [J].Mechanics in Engineering, 2010, 32(3): 22-25.

[5] KOHNO H, BATHE K J.A nine-node quadrilateral FCBI element for incompressible fluid flows [J].Communications in Numerical Methods in Engineering, 2006, 22(8): 917-931.

[6] BROOKS A N, HUGHES T J R.Streamline upwind/Petrov-Galerkin formulation for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations [J].Computer Methods in Applied Mechanics and Engineering, 1982, 32(1/2/3): 199-259.

[7] JAMESON A.Time dependent calculation using multigrid with applications to unsteady flows past airfoils and wings [C]∥Proceedings of AIAA 10th Computational Fluid Dynamics Conference.Reston, VA, USA: AIAA, 1991: 1-8.

[8] NITHIARASU P, CODINA R, ZIENKIEWICZ O C.The characteristic-based split (CBS) scheme: a unified approach to fluid dynamics [J].Numerical Methods in Engineering, 2006, 66(10): 1514-1546.

[9] ADINA R&D Inc.ADINA CFD&FSI: theory and modeling guide [M].Watertown, MA, USA: ADINA R&D Inc., 2005.

[10]DONEA J, HUERTA A.Finite element methods for flow problems [M].London, UK: John Wiley & Sons, 2003: 92-93.

[11]GRESHO P M, SANI R L.Incompressible flow and the finite element method [M].New York, USA: John Wiley & Sons, 2000: 302.

[12]TRYGGVASON G.Numerical simulation of the Rayleigh-Taylor instability [J].Journal of Computational Physics, 1988, 75(2): 253-282.

[13]CALGARO C, CREUSE E, GOUDON T.A hybrid finite volume-finite element method for variable density incompressible flows [J].Journal of Computational Physics, 2008, 227(9): 4671-4696.

[14]GUERMOND J L, QUARTAPELLE L.A projection FEM for variable density incompressible flows [J].Journal of Computational Physics, 2000, 165(1): 167-188.

[15]GUERMOND J L, SALGADO A.A splitting method for incompressible flows with variable density based on a pressure Poisson equation [J].Journal of Computational Physics, 2009, 228(8): 2834-2846.

[本刊相關(guān)文獻(xiàn)鏈接]

趙立波,徐龍起,熱合曼艾比布力,等.矩形微懸臂梁的流固耦合諧振頻率分析.2013,47(11):60-64.[doi:10.7652/xjtuxb201311011]

何聯(lián)格,左正興,向建華.氣缸蓋中兩相流沸騰換熱熱機(jī)耦合仿真分析.2013,47(7):23-28.[doi:10.7652/xjtuxb201307 005]

李連忠,牛文全,魏正英,等.微灌壓力調(diào)節(jié)器調(diào)壓特性流固耦合數(shù)值計(jì)算及分析.2013,47(5):131-136.[doi:10.7652/xjtuxb201305024]

何聯(lián)格,左正興,向建華.氣缸蓋冷卻水腔內(nèi)兩相流動沸騰傳熱仿真研究.2013,47(1):21-26.[doi:10.7652/xjtuxb 201301005]

張穎莉,種道彤,劉繼平,等.方管內(nèi)混合對流與管壁導(dǎo)熱耦合換熱的數(shù)值模擬.2012,46(5):19-24.[doi:10.7652/xjtuxb201205004]

劉小民,王星,許運(yùn)賓.運(yùn)動罐體內(nèi)液體晃動的雙向流固耦合數(shù)值分析.2012,46(5):120-126.[doi:10.7652/xjtuxb201205021]

張慧賢,寇子明,吳娟,等.液壓激波作用下管道流固耦合的動力學(xué)建模.2012,46(3):94-99.[doi:10.7652/xjtuxb201203 017]

康偉,張家忠,李凱倫.利用本征正交分解的非線性Galerkin降維方法.2011,45(11):58-62.[doi:10.7652/xjtuxb201111 011]

梅冠華,張家忠.時滯慣性流形在三維壁板顫振數(shù)值分析中的應(yīng)用.2011,45(9):40-46.[doi:10.7652/xjtuxb201109008]

蘇波,錢若軍,韓向科.一種用于流固耦合分析的有限元網(wǎng)格簡捷更新方法.2011,45(3):16-24.[doi:10.7652/xjtuxb 201103003]

(編輯 葛趙青)

ModifiedStreamlineUpwindPetrov-Galerkin(SUPG)StrategyforCalculationofThree-DimensionalHeterogeneousFlowProblems

SU Bo1,HAN Xiangke2

(1.Faculty of Civil Engineering and Mechanics, Jiangsu University, Zhenjiang, Jiangsu 212013, China;2.CMTCC Shanghai Shisanye Construction Co., Ltd., Shanghai 200092, China)

By introducing the dual-time stepping method and the variable splitting algorithm, a modified SUPG strategy is developed based on the stable streamline upwind Petrov-Galerkin (SUPG) finite element method, where the traditional assumption of constant density for incompressible flow problem is abandoned and the density transportation equation is introduced into the governing equations.The velocity and pressure fields are discretized with interpolating function of the same order, thus finite element scheme of the modified SUPG strategy gets simple and clear, and the order of algebraic equations is reduced.The dual-time stepping method is also introduced to enhance calculation stability of the SUPG strategy for complex unsteady problems.A free flow with heterogeneous, unsteady field of three-dimensional rectangular pipe under gravity and the whole relative motion between two types of liquids with different density are analyzed.The calculation results indicate that the velocity and pressure fields distribute and transmit smoothly with time and no numerical wave occurs in the case of greater time steps; the vortex position and its varying regulation coincide well with the results in the classic literatures without jumps and discontinuities.Example proves the numerical stability and accuracy of the modified SUPG method.

incompressible flow; finite element method; splitting algorithm; streamline upwind Petrov-Galerkin (SUPG) method

10.7652/xjtuxb201403023

2013-08-05。

蘇波(1977-),男,博士,講師。

國家自然科學(xué)基金青年基金資助項(xiàng)目

(51108210);江蘇省博士后基金資助項(xiàng)目(1301048C);國家自然科學(xué)基金專項(xiàng)數(shù)學(xué)天元基金資助項(xiàng)目(11226308)。

時間: 2013-12-25

O357.1

:A

:0253-987X(2014)03-0128-07

網(wǎng)絡(luò)出版地址: http:∥www.cnki.net/kcms/detail/61.1069.T.20131225.1702.005.html