一階帶脈沖泛函微分方程的周期邊值問題

楊向輝

（武漢工程大學理學院智能機器人湖北省重點實驗室，湖北 武漢 430073）

一階帶脈沖泛函微分方程的周期邊值問題

楊向輝

（武漢工程大學理學院智能機器人湖北省重點實驗室，湖北 武漢 430073）

本文利用不動點定理，上下解方法結合單調迭代技術，討論了下列一階帶脈沖泛函微分方程的周期邊值問題極值解的存在性.

脈沖微分方程；不動點定理；上下解；單調迭代方法

脈沖微分方程是近年來發展起來的微分方程的一個重要分支，它較之相應的不帶脈沖的微分方程更能精確的描述某些現象.因而脈沖微分方程的研究已引起了大量學者的興趣[1-2]，而周期邊值問題一直是脈沖微分方程理論的一個重要部分，是目前比較活躍的研究領域，吸引了眾多學者，取得了很多好的結果.

眾所周知，在求常微分方程或具有固定時刻脈沖微分方程的極值解時，單調迭代技術結合上，下解方法是一種非常有效的方法，將此方法應用到具有變動時刻脈沖微分方程系統，近年來也獲得了許多結果，其中關于一階，二階帶脈沖泛函微分方程的周期邊值問題也已經有了大量的研究[3-6]，在[7]中Nieto and Rodriguez-Lopez提出了一個新的上，下解的定義來討論了如下周期邊值問題

在此基礎上，本文采用相似的關于上，下解的定義，討論了如下周期邊值問題

定義1稱α(t)∈E是PBVP（1）的一個下解，如果它滿足

其中

定義2β(t)∈E稱是PBVP（1）的一個上解，如果它滿足

其中

引理1 設u∈E，滿足

其中M>0,N≥0,0≤Lk<1,k=1,2,L,pLk≤1，則當t∈J+時，u(t)≥0.

引理2 設u∈E，滿足

引理3 設u∈E是(5)的解，當且僅當u是下列脈沖積分方程的解

其中

定理1 假設下列條件成立：

(H1)α,β∈E分別是PBVP(1)的下解和上解,且α(t)≤β(t), t∈[-r,T].

(H2)M>0,N≥0,函數f滿足

其中

(H3)函數Ik滿足

其中α(t)≤x≤y≤β(t)，0≤Lk≤y<1，k=1,2,L,p,

則存在單調序列{αn(t)},{βn(t)}令α0(t)=α(t),β0(t)=β(t)使得,在J+上一致成立，其中p(t)，q(t)是

PBVP（1）在J+介于α(t)與β(t)之間的最小解與最大解.

證明對?η∈[α，β]，定義算子A：[α，β]→E為x=Aη，其中x是線形PBVP(5)的唯一解,則算子具有下列性質：

(ⅰ)α≤Aα；β≥Aβ

(ⅱ)A是[α，β]中的單調算子，即對任意η1，η2∈[α，β]，如果η1≤η2有Aη1≤Aη2，為證明(ⅰ)令α1=Aα，m=α1-α，其中α1滿足(5),下分兩種情況

情況1:α(0)≤α(T)

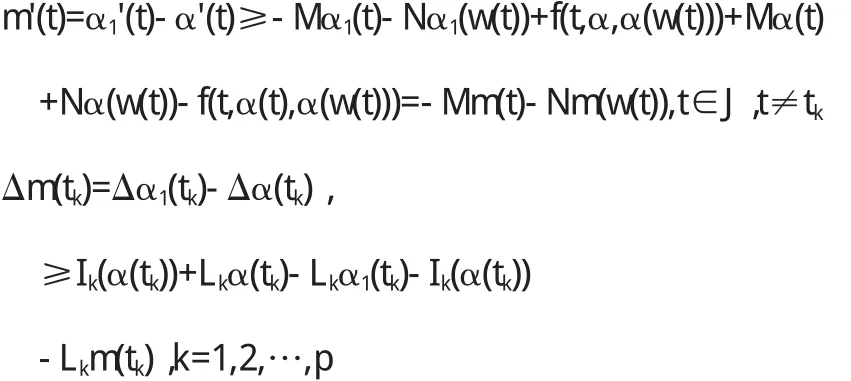
m(t)=α(t)-α1(t)=m(0)≥m(T)，t∈[-r,0]

由引理1,有m(t)≥0,即Aα≥α.

情況2α(0)>α(T)

容易驗證

由引理2，m(t)≥0,即Aα≥α.

類似的,我們可證明Aβ≤β.

下證(ⅱ)令x=Aη1，x2=Aη2，m=x2-x1

其中η1≤η2，η1，η2∈[α,β],

m(t)=x2(t)-x1(t)=m(0)=m(T)t∈[-r,0]

由引理1，有m(t)≥0,對任意t∈J+成立，即x1≤x2.

定義函數序列{αn(t)}，{βn(t)}如下

由算子(ⅰ)，(ⅱ)的性質有

每一αn，βn∈E,n=1,2,L，滿足PBVP

于是存在p,q使得

在[-r,T]上一致成立，顯然p,q滿足PBVP(1).

下證p,q是PBVP(1.2.1)的極值解,設x(t)∈[α(t)，β(t)]是（1）的任意解，假設存在正整數n使得αn(t)≤x(t)≤βn(t)，t∈J+,設m=x-αn有

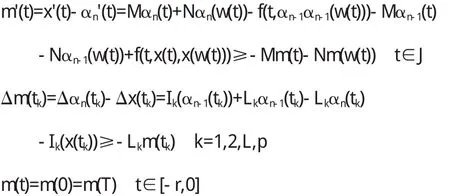
由引理1，m(t)≥0，對任意t∈J+成立，即x(t)≥αn(t).

類似的，我們可得到x(t)≤βn(t)對任意t∈J+成立.

由歸納法，對所有n，αn(t)≤x(t)≤βn(t)成立.于是，令n→∞有p≤x≤q.證畢.

〔1〕V.Lakshm ikantham,D.D.Bainove,P.S.Semeonov, Theory of impulsive differential equations,Singapore: W orld Scientific,1989.

〔2〕D.D.Bainov,P.S.Simeonov,Impulsive differential equations:Periodic solutions and applica-tions,Harlow, Longman,1993.

〔3〕Zhim in He,Xiaom in He,Monotone iterative technique for impulsive integro-differential equations w ith periodic boundary conditions，Comp.Math.Appl,48(2004),73-84.

〔4〕J.J.Nieto,Periodic boundary value problem for first-order impulsive ordinary differential equations,Non.Anal, 51(2002),1223-1232.

〔5〕Daqing Jiang,Junjie Wei,Monotone method for first and second-order periodic boundary value problem and periodic solutions of functional differential equations，Non.Anal,50(2002),885-898.

〔6〕韋忠禮.二階混合型脈沖微分-積分方程周期邊值問題解的存在性.數學學報,1996（2）：531-539.

〔7〕J.J.N ieto,Remarks on periodic boundary value problems for functional differential equations,J.Comp.Appl.Math, 158(2003),339-353.

O29

A

1673-260X（2014）09-0001-03