薄膜傳輸系統(tǒng)導向輥的力學特性分析

馬利娥,梅雪松,李彥鋒,武吉梅,萬清泉

(1.西安交通大學機械工程學院, 710049, 西安; 2.西安理工大學印刷包裝工程學院, 710048, 西安; 3.西安交通大學機械制造系統(tǒng)工程國家重點實驗室, 710049, 西安; 4.陜西北人印刷機械有限責任公司, 714000, 陜西渭南)

薄膜傳輸系統(tǒng)導向輥的力學特性分析

馬利娥1,2,梅雪松1,3,李彥鋒4,武吉梅2,萬清泉2

(1.西安交通大學機械工程學院, 710049, 西安; 2.西安理工大學印刷包裝工程學院, 710048, 西安; 3.西安交通大學機械制造系統(tǒng)工程國家重點實驗室, 710049, 西安; 4.陜西北人印刷機械有限責任公司, 714000, 陜西渭南)

為了提高薄膜傳輸的精度和穩(wěn)定性,根據導向輥的結構特點,建立了多體組合的有限元模型,分析了導向輥的撓曲變形、模態(tài)、諧響應和不平衡激勵變形,并對靜態(tài)時的撓曲變形進行了試驗測試。研究結果表明:導向輥的壁厚、輥體長度和軸頭長度等是影響導向輥力學特性的主要因素;采用目前企業(yè)常用的導向輥結構參數和生產工藝參數,導向輥在薄膜張力、自身重力以及不平衡質量激勵下的最大變形值為52.725μm;如果將導向輥筒體的壁厚從4.5mm減小為3.5mm,其他條件不變,雖然會使導向輥結構的最大變形值提高為58.108 μm,但臨界轉速可從8 255.1 r/min提高到8 309.94 r/min,隨動比則可從0.920提高到0.982,從而有利于提高薄膜傳輸的精度和穩(wěn)定性。

導向輥;薄膜傳輸;有限元分析;力學特性

近年來,在信息和能源領域開始應用的新型柔性電子薄膜產品(有機發(fā)光二極管、電子標簽和光學薄膜等)采用的是卷繞式收、放料的加工方式。在加工過程中,薄膜在眾多導向輥對其進行導入、定向和支撐的張緊狀態(tài)下高速地傳輸,對傳輸精度要求很高。薄膜通過導向輥時常出現接觸表面的劃傷、偏移和皺褶等不穩(wěn)定傳輸故障,嚴重制約著柔性電子薄膜產品的制備質量和效率[1]。薄膜的傳輸過程示意圖如圖1所示。

圖1 薄膜傳輸系統(tǒng)示意圖

導向輥是薄膜傳輸設備中數量最多、分布最廣、影響最大的部件。導向輥屬于被動輥,由薄膜通過摩擦力帶動旋轉,薄膜傳輸精度越高,要求導向輥的隨動性越好,目前行業(yè)中使用的導向輥的隨動比為0.920。高精密薄膜在高速傳輸時容易產生劃傷、皺褶、偏移和振動,而導向輥的結構和力學特性對薄膜的傳輸穩(wěn)定性具有重要的影響,是導致薄膜發(fā)生劃傷和套印不準的主要原因,對薄膜的加工速度和精度的提高起著決定性的作用[2-5]。

Hashimoto采用接觸力學的理論研究了紙帶和導向輥之間的摩擦力特性[6]。Hikita等通過分析導向輥表面的刻線分布方式,研究了薄膜經過導向輥時的打滑和起皺現象[7]。Tran等利用激光傳感器測量了薄膜在導向輥處的振幅,發(fā)現當導向輥的表面結構不同時,薄膜的振動特性也不相同[8]。目前,由于缺乏關于導向輥結構對薄膜傳輸穩(wěn)定性影響的理論基礎,因此在實際應用中只是通過提高導向輥的安裝和加工精度來實現薄膜的穩(wěn)定傳輸[3-5]。

導向輥是薄壁圓筒輥身的多體組合的不規(guī)則細長件,在薄膜張力及自身重力作用下容易發(fā)生撓曲變形。因此,本文通過分析導向輥的結構特點,建立導向輥的有限元模型,來研究導向輥的靜態(tài)特性和動態(tài)特性,以期為合理優(yōu)化導向輥的結構,減少運動薄膜發(fā)生偏移、振動、皺褶和劃傷等現象,提高薄膜的傳輸穩(wěn)定性提供理論基礎。

1 導向輥的靜力學特性研究

1.1 導向輥有限元模型的創(chuàng)建

導向輥的結構如圖2所示,由軸頭、堵頭和筒體采用熱裝方式形成,以減小導向輥圓周方向的擾動[9]。

(a):軸頭;(b):堵頭;(c):筒體;(d):導向輥

本文研究的導向輥的筒體壁厚為4.50 mm,導向輥直徑為120.00 mm,筒體長為1 100.00 mm,軸頭長為110.00 mm,屬于多體組合的細長件。根據導向輥的結構特點對其進行有限元模型創(chuàng)建[10-12]:先建立導向輥內部加強筋,再將導向輥筒體拆分為2個薄壁環(huán),將堵頭拆分為2部分,軸頭拆分為4部分,建立導向輥的結構模型。導向輥的三維模型使用的單元類型為3D solid185,支軸選用梁單元Beam188,軸承對導向輥的作用采用Combination14單元進行模擬。

對實體模型劃分單元后,通過在導向輥軸端軸承連接處與梁的中心節(jié)點建立直線梁單元,仿真支軸對軸承及導向輥的作用。支軸的梁類型為實心圓柱,半徑為7.5mm,長度為46 mm。通過在ANSYS中施加彈簧單元來仿真軸承對導向輥的作用[13-14],得到該彈簧單元的剛度K為16.325MN/m。整個有限元模型的單元數量為64 956,節(jié)點總數為78 912。導向輥結構的有限元模型如圖3所示。

圖3 導向輥結構的有限元模型

1.2 載荷及邊界條件的確定

將薄膜與導向輥接觸區(qū)域對應的導向輥的圓心角稱為薄膜與導向輥的包角(θ,見圖4),薄膜在傳輸時處于受拉狀態(tài),薄膜張力為T,導向輥所受的壓力為P。通常印刷薄膜的張力為3.0～30.0 kg/m,這里取薄膜張力為20.0 kg/m,包角θ為90°,薄膜幅面寬度為1 050.00 mm,通過計算得到導向輥所受的壓力P為291.0 N,轉化為面壓力p,其值為2 940.577 N/m2。

圖4 薄膜張力與導向輥壓力示意圖

對導向輥施加梁單元外節(jié)點位移全約束和x方向重力加速度9.8 m/s2的邊界條件,導向輥的有限元模型如圖5所示。

圖5 導向輥邊界條件及載荷有限元模型

1.3 導向輥撓曲變形仿真分析

圖6 靜態(tài)時導向輥的撓曲變形曲線

對導向輥進行靜力學分析,得到靜態(tài)時導向輥的撓曲變形曲線,如圖6所示。由圖6可知,靜態(tài)時導向輥的最大變形發(fā)生在輥體中間處,變形向兩邊逐漸減小。

在導向輥變形云圖中提取的節(jié)點坐標與位移值見表1。由表1可知,導向輥最大位移發(fā)生在16 076號節(jié)點,其變形值為51.208 μm,輥體外壁x方向節(jié)點的位移值基本對稱。

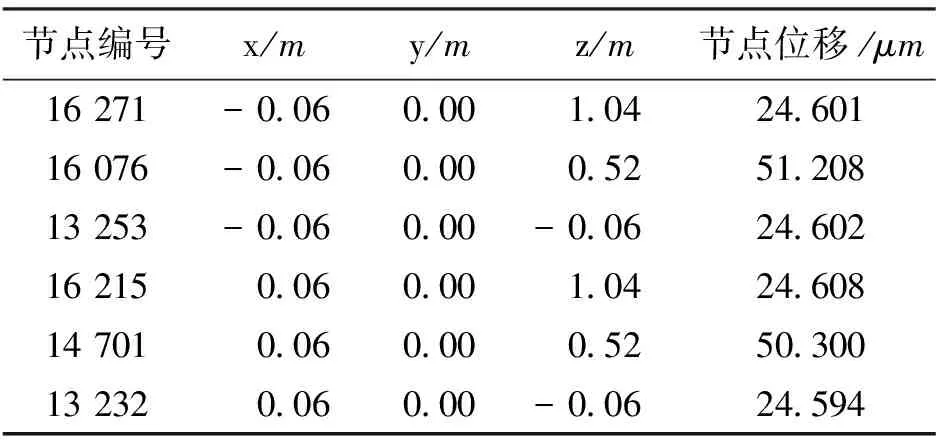
表1 變形云圖中提取的節(jié)點坐標值與位移值

1.4 導向輥撓曲變形的測試

采用陜西北人凹版印刷機放卷單元的導向輥進行撓曲變形測定試驗。導向輥筒體壁厚為4.50 mm,導向輥直徑為120.00 mm,筒體長為1 300.00 mm,軸頭長為160.00 mm。在薄膜與導向輥的包角為90°、薄膜張力為20.0 kg/m時,對薄膜施加不同的張力,采用CM-1J-10型靜態(tài)電阻應變儀測得導向輥中間位置處的應變,結果見表2。

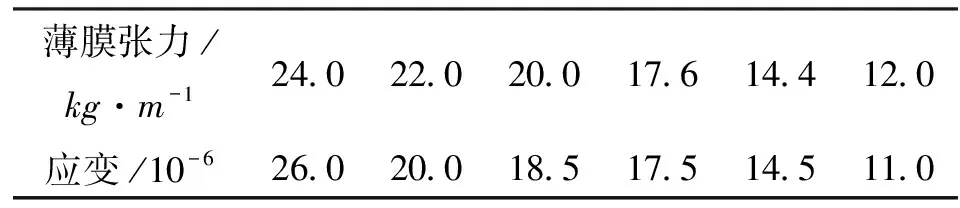
表2 導向輥中間位置處的應變測量結果

由表2可知,當薄膜張力為20.0 kg/m時,中間位置處的應變?yōu)?8.5×10-6,計算得導向輥的最大變形值為53.40 μm,比理論仿真結果略大。這是因為試驗中使用的導向輥軸頭和筒體的長度比理論計算時使用的略長所致。總體而言,試驗測試結果與理論和仿真結果是一致的。

理論計算、仿真和試驗測試的結果相一致,說明了本文所建立的有限元模型的正確性。

2 導向輥的動態(tài)特性研究

假設導向輥為剛性支撐。在上述靜力學特性研究的基礎上,繼續(xù)進行導向輥的動態(tài)特性研究[15-16]。

2.1 導向輥的模態(tài)分析

導向輥結構是一種連續(xù)結構,經離散化后就變成了一個多自由度系統(tǒng)。根據第1節(jié)介紹的有限元理論及振動力學,對于一個多自由度的線彈性系統(tǒng),其運動微分方程可由下式給出

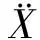
(1)

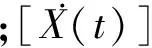
(2)

其解的一般形式為

[X(t)]=[X0]sin(ωt+φ)

(3)

式中:ω為系統(tǒng)的固有頻率;[X0]為系統(tǒng)響應的振幅向量矩陣。將式(3)代入式(2),得到

(4)

自由振動結構各個節(jié)點的振幅不全為零,因此[Xi]≠0,根據克萊姆法則有

(5)

求解式(4)中的ω2和[X0]是一個廣義特征值問題。模態(tài)分析就是一種坐標變換過程,即由物理坐標變換到模態(tài)坐標的過程,通過解存在耦合關系的方程,得出系統(tǒng)的模態(tài)參數。稱坐標變換矩陣為模態(tài)矩陣,模態(tài)振型就是矩陣中的每個列向量,振動系統(tǒng)的n個自由度對應n階主振型和n個固有頻率。導向輥的模態(tài)分析Campbell圖如圖7所示,該圖是三維圖形的二維表達。

圖7 導向輥模態(tài)分析Campbell圖

圖7中導向輥的前4階固有頻率曲線為導向輥正轉和反轉時的固有頻率的表達。本研究僅考慮由內部質量不均造成的動模態(tài)。激振力曲線和頻率曲線相交,交點A就是可能的共振點,對應的一階固有頻率為137.585Hz,一階固有頻率下的臨界轉速為863.921 rad/s,經計算,對應的導向輥的臨界轉速為8 255.1 r/min。當凹版印刷機在薄膜傳輸速度400 m/min下運行時,該導向輥結構相應的最大轉速為1 061.03 r/min,遠遠小于其臨界轉速。

2.2 導向輥的諧響應分析

對于導向輥結構,在計算動力學特性時將其等效為轉子系統(tǒng)。轉子系統(tǒng)存在的不平衡激勵是轉子動力學特性研究的重要領域。導向輥屬于周期對稱結構,通過動平衡試驗得到導向輥外徑上存在的不平衡質量m為0.005kg,對該不平衡質量激勵引起的導向輥變形進行仿真分析,可以得出不同轉速時轉子在一定不平衡激勵下的響應。

不平衡質量m對于導向輥軸線會產生偏心距e,單自由度旋轉不平衡質量所引起的自激勵模型如圖8所示。不平衡質量m在導向輥旋轉過程中會產生離心力F,其大小為

F=mRω2

(6)

Fx=Fcos(ωt+φ);Fy=Fsin(ωt+φ)

(7)

圖8 不平衡質量引起的導向輥自激勵模型圖

設初始狀態(tài)φ為0°,由以上分析知,該不平衡質量對轉子系統(tǒng)的影響相當于在軸心處加了2個按周期變化的正弦和余弦簡諧激勵力,所以可以按照ANSYS中動力學分析的諧響應分析方法計算不平衡質量引起的響應。

根據式(6)和式(7),可求得不同轉速下不平衡質量引起的激勵力,即表3中的離心力F。

根據薄膜傳輸速度的不同,采用Full方法進行諧響應分析。激勵力頻率為0～200 Hz,設置迭代子步數為50,給導向輥施加自轉速度,分別對5種不同薄膜傳輸速度施加不同的導向輥自轉速度,得到導向輥在不同薄膜傳輸速度下不平衡激勵引起的響應。圖9給出了薄膜傳輸速度為400 m/min時導向輥的響應曲線。

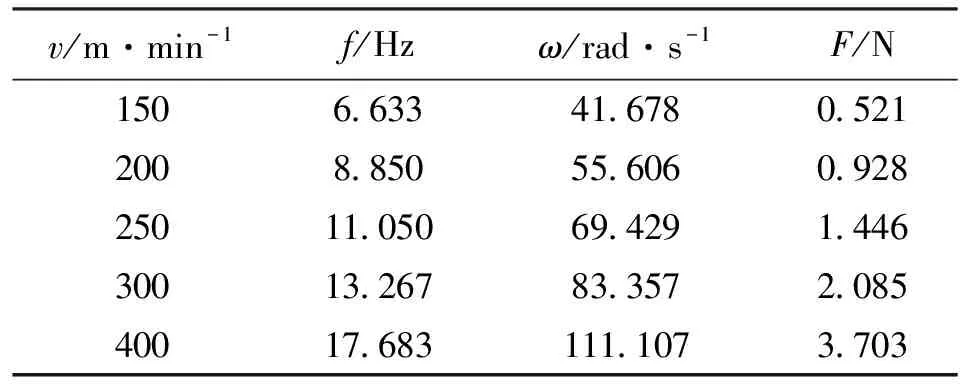
表3 導向輥外徑上的不平衡質量引起的激勵力

從圖9可以看到,導向輥結構在125Hz處出現了最大幅值,這是由于在此處,激振力頻率與導向輥的一階固有頻率相近,導向輥結構發(fā)生了共振,而此時該導向輥結構的最大轉速遠遠小于其臨界轉速。通過諧響應分析,可知導向輥結構可以進行改進。

圖9 v=400 m/min時的導向輥諧響應曲線

2.3 導向輥的不平衡激勵變形分析

導向輥外徑上存在的不平衡質量旋轉所產生的離心力是造成導向輥受迫振動的主要原因之一,通過對導向輥結構的不平衡響應進行計算,可以得出不平衡質量在不同薄膜傳輸速度下引起的導向輥撓曲變形。

當薄膜傳輸速度達到穩(wěn)定后,由于不平衡質量的存在,導向輥會產生不平衡的響應,本節(jié)通過ANSYS中的Transient模塊對導向輥達到穩(wěn)定運轉速度后的變形進行計算。對導向輥進行時域分析時,在導向輥筒體表面加載的激勵力如圖10所示。

由圖10可知,不同薄膜傳輸速度下激勵力的變化呈現周期性。導向輥的最大撓曲變形值見表4,均出現在導向輥軸線中間截面的節(jié)點上。在薄膜傳輸速度為400 m/min時,單個旋轉周期內由不平衡質量引起的導向輥結構的最大變形量為0.844 μm。

表4 不平衡質量引起的導向輥最大撓曲變形量

由以上分析結果可知,在不同的薄膜傳輸速度下,導向輥的變形不同,薄膜傳輸速度越高,導向輥所產生的變形就越大。在薄膜傳輸速度為400m/min時,導向輥的變形云圖如圖11所示。

曲線1:Fy=10.509sin41.678t;曲線2:Fy=18.795sin55.506 2t;曲線3:Fy=29.204sin69.429 2t;曲線4:Fy=42.138sin83.356 9t;曲線5:Fy=74.879sin111.107t

圖11 薄膜傳輸速度為400 m/min時導向輥的變形云圖

將靜力分析與不平衡響應分析得到的導向輥變形量進行疊加,得到導向輥在不同薄膜傳輸速度下的最大變形量,見表5。從表5可以看到:隨著薄膜傳輸速度的增加,變形值逐漸增大;當薄膜傳輸速度為400m/min時,筒體壁厚為4.5mm的導向輥的最大總變形量為52.725μm。

表5 導向輥的最大總變形量

3 結 論

本文采用有限元分析的方法研究了導向輥的結構特點和力學特性,主要結論如下。

(1)導向輥的撓曲變形主要受其長度、壁厚、支撐情況的影響,當導向輥筒體壁厚為4.5mm、直徑為120 mm、筒體長為1 100 mm、軸頭長為110 mm、薄膜張力為20.0 kg/m、薄膜傳輸速度為400 m/min時,導向輥結構在薄膜印刷張力、自身重力以及不平衡質量激勵下的最大變形量為52.725μm,最大變形發(fā)生在導向輥軸線方向中間處。

(2)該導向輥結構的一階臨界角速度為863.921 rad/s,對應的頻率為137.585Hz,臨界轉速為8 255.1 r/min。目前導向輥的實際轉速遠小于臨界轉速。

(3)如果將導向輥筒體壁厚減小為3.5mm,其他條件不變,采用同樣方法可以求得導向輥結構在薄膜印刷張力、自身重力以及不平衡質量激勵下的最大變形量為58.108 μm,一階臨界角速度為869.617 rad/s,對應的頻率為138.499 Hz,臨界轉速為8 309.94 r/min,此時隨動比可提高至0.982。

(4)隨著薄膜傳輸速度增加,導向輥的撓曲變形增大,但增大的幅度有限。綜合來看,導向輥的結構參數,如導向輥的壁厚、輥體長度和軸頭長度等,是影響導向輥力學特性的主要因素。

[1] SONDERGAARD R R, HOSEL M, KREBS F C.Roll-to-roll fabrication of large area functional organic materials [J].Journal of Polymer Science: Part B Polymer Physics, 2013, 51(1): 16-34.

[2] BRANCA C, PAGILLA P R, REID K N.Governing equations for web tension and web velocity in the presence of non-ideal rollers [J].ASME Journal of Dynamic Systems, Measurement, and Control, 2013, 135(1): 011018.

[3] KIM C H, JO J, LEE S H.Design of roll-to-roll printing equipment with multiple printing methods for multi-layer printing [J].Review of Scientific Instruments, 2012, 83(6): 065001.

[4] KIM C H, YOU H I, LEE S H.Register control of roll-to-roll gravure-offset printing equipment considering time difference between measurement and actuation [J].IME Journal of Mechanical Engineering Science, 2012, 226(11): 2726-2738.

[5] PAGILLA P R, DIAO Y.Resonant frequencies in web process lines due to idle rollers and spans [J].ASME Journal of Dynamic Systems, Measurement, and Control, 2011, 133(6): 061018.

[6] HASHIMOTO H.Friction characteristics between paper and steel roller under mixed lubrication [J].IME Journal of Engineering Tribology, 2012, 226(12): 1127-1140.

[7] HIKITA S, HASHIMOTO H.Improvement of slippage and wrinkling of transporting webs using micro-grooved rollers [J].Journal of Advanced Mechanical Design, Systems, and Manufacturing, 2010, 4(1): 226-237.

[8] TRAN S B Q, YOO Y H, KO J H.Experimental and numerical study of air entrainment between web and spirally grooved roller [J].ASME Journal of Tribology, 2009, 131(2): 021502.

[9] 王曉敏.薄膜導向輥的加工要點 [J].印刷技術, 2012(9): 54-55.

WANG Xiao-min.Processing main methods of web roll [J].Printing Technology, 2012(9): 54-55.

[10]程昌鈞, 朱媛媛.彈性力學 [M].上海: 上海大學出版社, 2005: 112-117.

[11]商躍進.有限元原理與ANSYS 應用指南 [M].北京: 清華大學出版社, 2005: 89-98.

[12]田紅亮, 方子帆, 朱大林, 等.固定接觸界面切向靜彈性剛度問題研究 [J].應用力學學報, 2011, 28(5): 458-464.

TIAN Hongliang, FANG Zifan, ZHU Dalin, et al.Investigation on tangential static elastic stiffness of fixed contact interface [J].Chinese Journal of Applied Mechanics, 2011, 28(5): 458-464.

[13]鄭子君, 陳璞, 王大鈞.桿、梁有限元模型的模態(tài)的振蕩性質 [J].振動與沖擊, 2012, 31(20): 79-83.

ZHENG Zi-jun, CHEN Pu, WANG Da-jun.Oscillation property of modes for FE models of bars and beams [J].Journal of Vibration and Shock, 2012, 31(20): 79-83.

[14]劉顯軍, 洪軍, 朱永生, 等.多支承軸系軸承受力與剛度的有限元迭代計算方法 [J].西安交通大學學報, 2010, 44(11): 41-45.

LIU Xianjun, HONG Jun, ZHU Yongsheng, et al.Iterative method to solve bearing’s force and stiffness for a multi-support spindle system based on finite element analysis [J].Journal of Xi’an Jiaotong University, 2010, 44(11): 41-45.

[15]ALI N J, GARCIA J M.Experimental studies on the dynamic characteristics of rolling element bearings [J].IME Journal of Engineering Tribology, 2010, 224(7): 659-666.

[16]劉海濤, 王磊, 趙萬華.考慮模態(tài)特性的高速機床進給系統(tǒng)剛度匹配研究 [J].西安交通大學學報, 2014, 48(1): 90-95.

LIU Haitao, WANG Lei, ZHAO Wanhua.Stiffness matching design for feed system of high speed machine tool [J].Journal of Xi’an Jiaotong University, 2014, 48(1): 90-95.

(編輯 葛趙青)

MechanicalBehaviorsofGuideRollerinWebTransferSystem

MA Li’e1,2,MEI Xuesong1,3,LI Yanfeng4,WU Jimei2,WAN Qingquan2

(1.School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2.School of Printing and Packaging Engineering, Xi’an University of Technology, Xi’an 710048, China;3.State Key Laboratory for Manufacturing Systems Engineering, Xi’an Jiaotong University, Xi’an 710049, China;4.Shaanxi Beiren Printing Machinery Co., Ltd., Weinan, Shaanxi 714000, China)

To improve the accuracy and stability of the web transfer, a multi-body combined finite element model is established according to the structural features of the guide roller.The guide roller bending deformation, the vibration modes, the harmonic response, and the deformation under unbalanced excitation are analyzed, and the experimental test of the static flexural deformation is performed.Research results show that the structural parameters of the guide roller, such as the wall thickness, the roller length, and the gudgeon length, etc., are the main factors influencing the guide roller mechanical behaviors.Keeping the structural parameters of the guide roller and other process parameters generally used in the industry unchanged, the maximum deformation value of the guide roller caused by its own gravity, the web tension and the unbalanced mass is 52.725μm.If the wall thickness of the guide roller is reduced to 3.5mm from 4.5mm, the maximum deformation of the guide roller is 58.108 μm while the critical speed is increased to 8 309.94 r/min from 8 255.10 r/min and the follow-up ratio is increased to 0.982 from 0.920, which is helpful to improve the accuracy and stability of web transfer.

guide roller; web transfer; finite element analysis; mechanical behavior

2014-02-20。

馬利娥(1973—),女,博士生,西安理工大學講師;梅雪松(通信作者),男,教授,博士生導師。

國家科技支撐計劃資助項目(2012BAF13B06);國家自然科學基金資助項目(51305341,11272253);陜西省教育廳重點實驗室科學研究計劃資助項目(13JS081)。

時間:2014-09-02

10.7652/xjtuxb201411015

TS803.6

:A

:0253-987X(2014)11-0086-06

網絡出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140909.0908.005.html