可滿足實例的歸結復雜度

沈靜，梅丹

海軍工程大學應用數學系，武漢 430033

可滿足實例的歸結復雜度

沈靜，梅丹

海軍工程大學應用數學系，武漢 430033

1 引言

約束滿足問題（Constraint Satisfaction Problem，CSP）由變量有限集合、值域集合、約束集合組成，通過為一組變量賦值來滿足一組給定的約束。約束滿足問題在人工智能、計算機科學等眾多應用領域都具有十分重要的意義。近年來，通過大量的實驗研究人們發現，在一些隨機CSP模型中，隨著控制參數r的變化，當變量個數n充分大時，存在某個臨界值r*，使得當r＜r*時，CSP模型產生的實例可滿足的概率趨近于1；而當r＞r*時，CSP模型產生的實例可滿足的概率趨近于0，人們稱此現象為相變現象，稱臨界值r*為“相變點”。隨著控制參數r的增加，求解實例的難度也發生了從易到難再到容易的變化，最難解的實例正好位于相變點附近。相變現象和算法分析之間的相關問題引起了國內外學者的極大關注[1-3]。

為了刻畫求解CSP模型實例的難度，人們對各種CSP模型的歸結復雜度進行分析[4-7]。歸結法是一種證明SAT實例不可滿足性的系統，其樹型歸結證明的長度與DPLL算法的運行時間有密切關系。1988年，Chvatal等人[8]證明了含有n個變量，cn個子句的隨機k-SAT問題在k≥3的情況下，具有指數級別的樹型歸結證明，故基于DPLL算法求解隨機k-SAT問題所花費的時間呈指數增長。2002年，Mitchell[9]按照一定的編碼規則，把一般CSP實例轉化為SAT實例，把轉化的SAT實例的歸結復雜度作為CSP實例的歸結復雜度，指出了如果實例對于歸結證明系統是難解的，則對基于歸結的算法也是難解的。

GRB模型[10]是近年來新提出的一種CSP模型，是RB模型[11-13]的推廣。它具有精確的可滿足相變現象，相變點r*=1。當r＞1時，隨著變量個數n趨近于無窮大，GRB模型的實例是不滿足的概率趨近于1，GRB模型的不可滿足實例對于樹型歸結證明具有指數下界[10]。當r＜1時，GRB模型的實例是可滿足的概率趨近于1，實驗顯示在相變點附近產生的可滿足實例也是難解的，如何刻畫可滿足實例的難解性?本文利用Achlioptas等人提出的方法[14]證明了：對于GRB模型在相變點附近產生的可滿足實例隨機選取一定的變量賦值，在求解過程中以很高的概率得到一個不可滿足的子問題，其子問題的歸結復雜度為2Ω(n)，因此從理論上證明了GRB模型在相變點附近產生的可滿足實例基于歸結的算法都是難解的。

2 GRB模型的定義

約束滿足問題以三元組I=(X,D,C)來描述約束滿足問題產生的實例，其中X=(x1,x2,…,xn)是n個變量的集合；值域D=(D1,D2,…,Dn)是X中各變量取值的集合；C=(C1,C2,…,Ct)是約束集合，且Ci=(Xi,Ri)，這里Xi=(xi1,xi2,…,xiki)是變量集合X的子集，其長度為ki，稱為約束作用域；Ri是Di1×Di2×…×Diki的子集，稱為約束關系。

設A=D1×D2×…×Dn，(a1,a2,…,an)∈A稱為X的一個賦值，即X中的每個變量都取定值域內的一個值。若(a1,a2,…,an)∈A滿足所有的約束，則稱這個賦值是可滿足的，否則稱這個賦值是不可滿足的。如果實例I存在可滿足的賦值，則稱實例I是可滿足的，否則稱實例I是不可滿足的。

設T是一個集合，|T|表示T中所含元素的個數。定義Ω(n)={f(n)：存在常數c＞0，使得f(n)≥cn}。如果n→∞時，事件εn成立的概率趨近于1，稱事件εn是幾乎成立的。

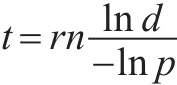
第1步：隨機可重復地選取長度為k的變量子集Xi=(xi1,xi2,…,xik)作為約束作用域。

第2步：隨機可重復地從Di1×Di2×…×Dik選取Ri作為約束關系，其中|Ri|=pdk，0＜p＜1。

理論上已經證明了GRB模型存在精確的相變現象。

3 歸結法

給定一個CNF公式F和子句C，如果存在一個子句序列π={C1,C2,…,Cm=C}，?Ci∈π，要么Ci∈F，要么Ci是由Cj和Ck(j,k≤i)基于以下規則推導出來的：

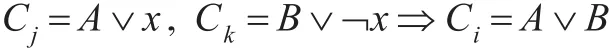
其中A和B是子句，x是一個命題變量，稱π是由CNF公式F推導出子句C的一個歸結。由CNF公式推導出空子句（記空子句為□）的歸結稱為公式F的歸結反演。

以π中的子句作為頂點，若Ci是由Cj和Ck推導出來的，則Ci和Cj，Ci和Ck之間分別用邊連接，這樣得到的圖Gπ如果是樹，則稱π是由CNF公式F推導出子句C的樹型歸結。

定義2（寬度）稱子句C中出現變量的個數為子句C的寬度，記作ω(C)。稱公式F中所有子句的最大寬度為公式F的寬度，記作ω(F)。稱歸結π中所有子句的最大寬度為π的寬度，記作ω(π)。稱所有由公式F推導出子句C的歸結π的最小寬度為由公式F推導出子句C的歸結寬度，記作ω(F?C)。

定義3（歸結復雜度）設π={C1,C2,…,Cm=□}是由公式F推導出空子句□的歸結，記

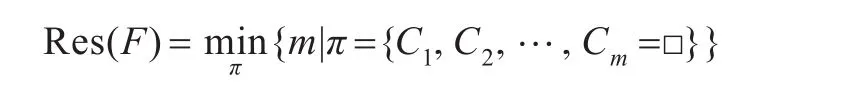
稱Res(F)為公式F的歸結復雜度。

定義4（子句復雜度）設π={C1,C2,…,Cm=C}是由公式F推導出子句C的歸結，μ(C)表示推出C的最小的子問題中所含變量的個數，稱μ(C)為子句C的復雜度。

定義5（自由變量）設P是實例I的子問題，給定變量x，P-x是子問題P中去掉含有變量x的約束后剩下的問題，如果任意滿足P-x的賦值能擴展為滿足子問題P的賦值，則變量x稱為自由變量。B(P)為P中所有自由變量的集合。

定義6（度）稱包含變量x的約束個數為變量x的度，記為deg（x）。

公式F是不可滿足的當且僅當公式F存在一個歸結反演。

Mitchell按照如下的編碼規則，把SAT實例的歸結復雜度推廣到一般的CSP實例。

（2）沖突子句：指每個約束中規定的不可滿足的賦值組。

（3）至多一個取值子句：指一個變量一次至多從值域中取一個值。

按照上述Mitchell規則構造相應的CNF公式，記為CNF（I）。公式CNF（I）有可滿足賦值當且僅當實例I有可滿足賦值。如果實例I有可滿足賦值，當xi=j時，設置xij=True，這樣可相應地產生公式CNF（I）的可滿足賦值。反之，若公式CNF（I）有一個可滿足賦值，當xij=True時，設置xi=j，可相應地產生實例I的可滿足賦值。稱公式CNF（I）的歸結復雜度Res（CNF（I））為實例I的歸結復雜度。

4 GRB模型可滿足實例的歸結復雜度

GRB模型的不可滿足實例對于樹型歸結證明具有指數下界[10]。當控制參數r＜1，GRB模型隨機產生的實例I幾乎是可滿足的，實驗顯示在相變點附近產生的可滿足實例是難解的。由于歸結證明是針對不可滿足實例而言的，但下面的引理證明了隨機選取θn個變量賦值后剩下的子問題P幾乎是不可滿足的，因此GRB模型的可滿足實例的歸結復雜度可轉換為子問題P的歸結復雜度。

引理1[5]設F為一個含有n個變量的CNF公式，若C為空子句□，則Res(F)≥2w(F?C)-w(F)。

由引理1可知，要證明CNF公式F的歸結復雜度為2Ω(n)，只需證明w(F?□)=Ω(n)。進一步，由歸結寬度的定義，只需證明在歸結反演中存在子句C，使得w(C)=Ω(n)。

定理3θ＞0，當1-θ＜r＜1時，設I是由GRB模型隨機產生的實例，隨機從n個變量中選取θn個變量賦值，賦值后剩下的子問題P幾乎沒有歸結復雜度小于2Ω(n)的樹型歸結證明。

證明設I是由GRB模型生成的一個隨機實例，GRB模型已經證明了下面兩個結論[10]：

假設存在含有s≤cn的子問題是不可滿足的，因此可得一個最小不可滿足的子問題I1，含有變量的個數s≤cn，由（1）知，子問題I1中至多有βslnd個約束。因此在I1中存在一個變量x，其度不超過kβlnd。由于I1是最小不可滿足的子問題，則I1-x是可滿足的，由（2）知變量x是自由變量，任意滿足I1-x的賦值能擴展為滿足子問題I1的賦值，與I1是最小不可滿足的子問題矛盾，故含有s≤cn的子問題是可滿足的。

Mitchell已經證明了，對于實例I，如果至多有s個變量的子問題是可滿足的，則I的每個歸結反演中存在一個滿足s/2≤μ(C)≤s的子句C[9]。

設實例I對應的CNF公式為CNF（I），由于含有s≤cn的子問題是可滿足的，在CNF（I）中存在子句C，其復雜度滿足cn/2≤μ(C)≤cn。設P1是使得CNF（P1）推導出子句C的最小子問題，故P1中至少有cn/2個變量，至多有cn個變量。由（1）知，P1中至多有βcnlnd個約束，至多有cn/3個變量的度大于3kβlnd。假設在P1中有變量x，如果變量x的度滿足deg(x)＜3kβlnd，由（2）知變量x是P1的自由變量。從P1中移去變量x和含變量x的約束，得到子問題P2，由P1的極小性，可得CNF（P2）不能推導出C，故能找到滿足P2但不滿足C的賦值Tx。若變量x的任何值域變量不出現在子句C中，則變量x的任何賦值都不影響C。由于賦值Tx不滿足C，故變量x的任何賦值都不滿足CNF（P1），與變量x是P1的自由變量矛盾，故變量x至少有一個值域變量出現在子句C中，即度不超過3kβlnd的變量都包含在子句C，則子句C的寬度滿足w(C)≥cn/2-cn/3=cn/6。因此P1中含有度不超過3kβlnd的變量至少有cn/6個。

取0＜θ＜c/6，對實例I隨機從n個變量中選取θn個變量賦值，P為賦值后的子問題，由定理1知P是不可滿足的。設賦值后P1剩下的子問題為超過3kβlnd的變量至少有個，類似上面的證明，度不超過3kβlnd的變量都包含在子句C中，因此由引理1可得子問題P幾乎沒有歸結復雜度小于2Ω(n)的樹型歸結證明。

5 結束語

由于在搜索解的過程中，產生了需要花很長時間求解的不可滿足的子問題，因此可將求解可滿足實例的難度和求解其不可滿足的子問題的難度聯系在一起，從理論上證明了GRB模型在相變點附近產生的可滿足實例在對θn個變量賦值后產生的子問題都是不可滿足的，這些不可滿足的子問題對于樹型歸結證明具有指數下界，因此用樹型歸結證明判定這些子問題的不可滿足性需要花指數級別的時間，由此證明了GRB模型在相變點附近產生的可滿足實例對基于歸結到算法是難解的。由于測試局部搜索算法需要可滿足的實例[13，15]，因此GRB模型在相變點附近產生的可滿足實例可作為測試局部搜索算法的平臺。

[1]CheesmanP，KanefskyB，Taylor W.Wherethereally hardproblems are[C]//Proceedings of IJCAI-91，1991：331-337.

[2]Mitchell D.Hard problems for CSP Algorithms[C]//Proceedings of 15th National Conf on Artificial Intelligence（AAAI-98），1998：398-405.

[3]Achlioptas D，Naor A，Peres Y.Rigorous location of phase transitions in hard optimization prolems[J].Nature，2005，435（7043）：759-764.

[4]Beame P，Karp R，Pitassi T，et al.The efficiency of resolutionandDavis-Putnamprocedures[J].SIAMJournal on Computing，2002，31（4）：1048-1075.

[5]Ben-Sasson E，Wigderson A.Short proofs are narrow-resolution made simple[J].Journal of ACM，2001，48（10）：149-169.

[6]Gao Y，Culberson J.Resolution complexity of random constraint satisfaction problems：Another half of the story[J]. Discrete Applied Mathematics，2005，153（1/3）：124-140.

[7]Molloy M，Salavatipour M R.The resolution complexity ofrandomconstraintsatisfactionproblems[J].SIAM，2007，7（3）：895-922.

[8]Chvatal V，Szemeraedi E.Many hard examples for resolution[J].Journal of the ACM，1988，35（4）：759-208.

[9]Mitchell D.Resolution complexity of random constraints[C]// Proceedings of the Eighth International Conference on Principles and Practices of Constraint Programming，Ithaca，NewYork，2002.

[10]ShenJ，Li L.Resolutioncomplexityof randomconstraint satisfaction problems with non-constant domain size[J].Journal of Information and Computational Science，2011，8（16）：4149-4156.

[11]Xu K，Li W.Exact phase transitions in random constraint satisfaction problems[J].Journal of Artificial Intelligence Reseach，2001，12（1）：93-103.

[12]Xu K，Li W.Many hard examples in exact phase transition[J].Theoretical Computer Science，2006，355（3）：291-302.

[13]Xu K，Boussemart F，Hemery F，et al.Random constrint satisfaction：Easy generation of hard satifiable instances[J]. Artificial Intelligence，2007，171（8/9）：514-534.

[14]Achlioptas D，Beame P，Molloy M.Exponential bounds for DPLL below the satisfiability threshold[C]//Proc 15th ACM-SIAM Symp Discrete Algorithms，2004：132-133.

[15]Achlioptas D，Gomes C，Kautz H，et al.Generating satisfiable probleminstances[C]//Proceedings of AAAI-00，2000：256-301.

SHEN Jing,MEI Dan

Department of Applied Mathematics,Naval University of Engineering,Wuhan 430033,China

The model GRB is a random model of constraint satisfaction problem,and it exhibits exact solubility phase transitions.For the experimental results that the satisfiability instances in the phase transition region are hard to solve,it uses the relation between the clause width and the resolution complexity to prove that almost all satisfiability instances of the model GRB have no tree-like resolution proofs of length less than exponential size.Therefore it shows theoretically that the satisfiability instances in the phase transition region are hard for the algorithms based on resolution.

resolution complexity;constraint satisfaction problem（CSP）;solubility phase transition

GRB模型是一種隨機約束滿足問題模型，此模型具有精確的可滿足相變現象。針對實驗中出現的GRB模型在相變區域產生的可滿足實例都是難解的現象，利用子句寬度和歸結復雜度的關系證明了GRB模型在相變點附近產生的可滿足實例對于樹型歸結證明具有指數下界。因此從理論上證明了在相變區域產生的可滿足實例對基于歸結的算法是難解的。

歸結復雜度；約束滿足問題；可滿足相變

A

TP301.5

10.3778/j.issn.1002-8331.1301-0137

SHEN Jing,MEI Dan.Resolution complexity of satisfiability instances.Computer Engineering and Applications, 2014,50（22）：69-72.

國家自然科學基金（No.11171370）。

沈靜（1980—），女，博士，講師，研究領域為人工智能；梅丹（1983—），女，碩士。E-mail：shendina@hotmail.com

2013-01-13

2013-02-25

1002-8331（2014）22-0069-04

CNKI網絡優先出版：2013-03-19,http://www.cnki.net/kcms/detail/11.2127.TP.20130319.1424.009.html