具有縱向可比性的體育模型經典參數檢驗方法
蘇 楊
1 研究目的
體育學是一門綜合性的學科,兼有社會科學和自然科學的雙重性質,其研究領域非常廣泛。實際問題的多樣性和復雜性決定了體育科研中統計學方法應用的復雜性。
近年來,計算機的普及和統計分析軟件的廣泛使用給建模帶來了便利[1]。統計檢驗是體育建模中的重點環節,如何正確地運用相應的統計檢驗方法,是體育統計應用中的重點和難點[2]。眾多檢驗方法相互關聯,有著相似甚至相同的特征。研究者若對統計理論理解不深,對統計方法掌握不夠全面,容易導致統計方法的運用生搬硬套[3]。T檢驗、方差分析和回歸分析是統計學中的三類經典參數檢驗方法。本研究通過綜合實例比較,探尋不同檢驗方法的使用條件及適用范圍,提高判別效率。
2 研究方法
文獻資料法,實例比較法。
3 結果與分析
3.1 基本概念
3.1.1 T檢驗
在體育科研和教學中,假設檢驗是常用的統計方法,假設檢驗分為參數檢驗和非參數檢驗[4]。在參數檢驗中較為廣泛采用的是T檢驗。
1)單個樣本T檢驗
單個樣本T檢驗(one-sample t-test)是在單個樣本的條件下,對此樣本的均值與指定的檢測值的進行比較。如檢驗某省18歲男生的平均身高所屬的總體均數μ,是否和已知的全國同年齡同性別的身高μ0相同。
2)配對樣本T檢驗
在體育科研和教學中,經常將研究對象設置實驗組和對照組,檢驗這兩組測試數據有無顯著差異,或是對同一批研究對象進行實驗前后的情況進行差異顯著性檢驗。這兩種樣本數據的比較,往往樣本含量小,須采用配對數據的t檢驗。
配對樣本T檢驗(paired-sample t-test)是比較同一對象在兩種不同條件下各種情況(如平均得分等)的均值異同。這里所說配對樣本是指樣本 x1,x2,……xn與 y1,y2,……ym 可以顛倒順序。如果獨立顛倒,就會改變問題的性質。
例:對8名隊員進行技術訓練,分別測得各人階段訓練前、后兩綜合成績x數據如下:
訓練前 x1:66,85,77,65,70,72,75,66;
訓練后 x2:70,75,80,72,84,65,83,67。
檢驗兩組數據差異是否顯著。取p=0.05。
3)獨立樣本T檢驗
獨立樣本T檢驗(independent t-test)是兩個對象在同一時間下的各種情況的均值比較。這里所說的獨立樣本是指樣本 x1,x2,……xn與 y1,y2,……ym,可以獨立顛倒順序而不對問題產生影響的樣本。
例如:調查對象是某班學生的跳高成績,一組樣本是男生的成績,另一組樣本是女生的成績。對它們可以任意顛倒學號的順序,而不對問題產生影響。
3.1.2 方差分析
方差分析(ANOVA)又稱變異數分析,有時也稱為F檢驗。方差分析是通過均值比較,研究某一個(one-way ANOVA)或多個因素(多指自變量)對因變量所引起的作用。
常見的單因素方差分析(one-way ANOVA)用于完全隨機設計的多個樣本均數間的比較,其統計推斷是推斷各樣本所代表的各總體均數是否相等。
單因素方差分析是把總變異的離均差平方和SS及自由度分別分解為組間和組內兩部分,其計算公式如下:SS組間=離均平方和/組間自由度 ;SS組內=離均平方和/組內自由度;SS總=SS組間+SS組內。
單因素方差分析:核心就是計算組間和組內離均差平方和。兩組或兩組以上數據,大組全部在一組就是組內,以每一組計算一均數,再進行離均平方和的計算:
SS組間=組間離均平方和,MS組間=SS組間/組數-1
SS組內=組內離均平方和,MS組內=SS組內/全部數據-組數
F值=MS組間/MS組內
注意:根據方差分析的這一結果,還不能推斷四個總體均數兩兩之間是否相等。如果要進一步推斷任兩個總體均數是否相同,應作兩兩比較。
3.1.3 回歸分析
在研究中,某個現象的發生或某種結果的得出往往與其他某個或某些因素相關,如果將存在相關的兩個變量,一個作為自變量,另一個作為因變量,并將兩者之間不十分確定、穩定的關系用數學方程式來表達,則可利用該方程由自變量的值來估計、預測因變量的值,這一過程稱為回歸分析。
近年來,隨著我國體育科學化的發展,在體育科研中,應用到的統計方法很多,最常見的是回歸分析,廣泛地應用于體育教學、訓練、管理中諸如預測、評估、控制及因素分析等多方面[5]。
3.2 實例用法比較研究
實例中數據的分析處理都是借助于SPSS20.0實現。
問題一:研究一組運動員在進行運動心理培訓前后的心理測試得分有無明顯差異。
在體育檢測中,絕大多數情況是總體正態或近似正態,而未知原總體方差,T檢驗適合小樣本且又可在方差未知的情形,在此我們選擇獨立樣本T檢驗。此檢驗的假設是:
原假設H。:運動員在進行運動心理培訓前后的心理測試得分無明顯差異;
備選假設H1:運動員在進行運動心理培訓前后的心理測試得分差異顯著。
進行兩個獨立樣本T檢驗后結果如下:
通過表1可以看出,t統計量的顯著(雙尾)概率小于0.05置信水平。所以拒絕原假設,接受H1,表明運動心理培訓對提高運動員心理素質有明顯作用。
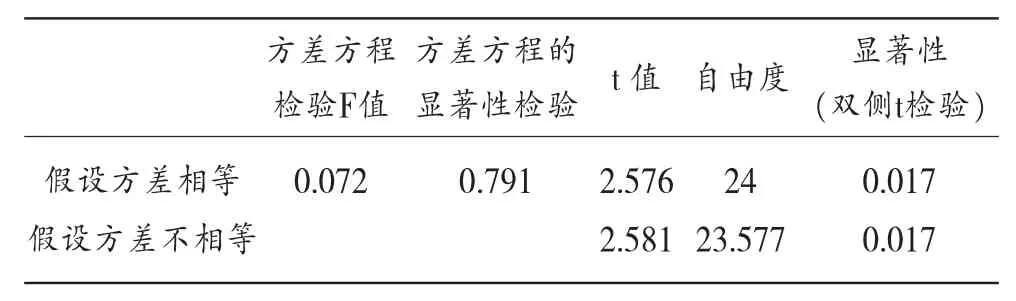
表1 雙樣本檢驗結果獨立樣本T檢驗
問題二:三種不同教學方案下學生的體育成績是否有差異。由于教學方案這個因變量是有三個不同的水平,故選擇單因素方差分析。此檢驗的假設是:
原假設H。:三種不同教學方案下學生的體育成績無差異;
備選假設H1:三種不同教學方案下學生的體育成績有顯著差異。
用單因素方差分析得出的結果如下:
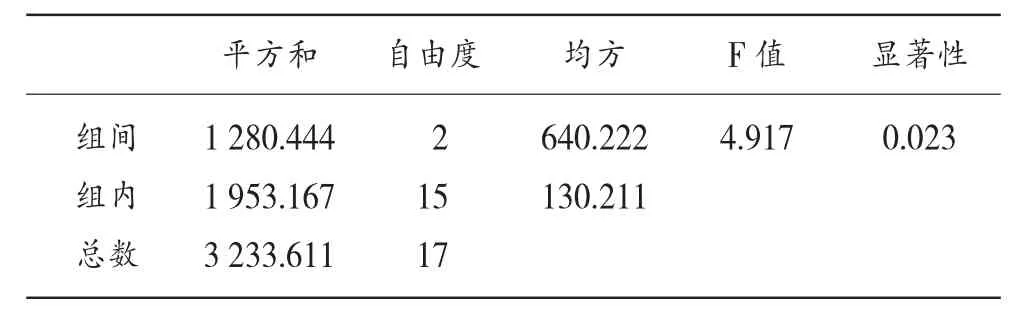
表2 方差分析表單因素方差分析
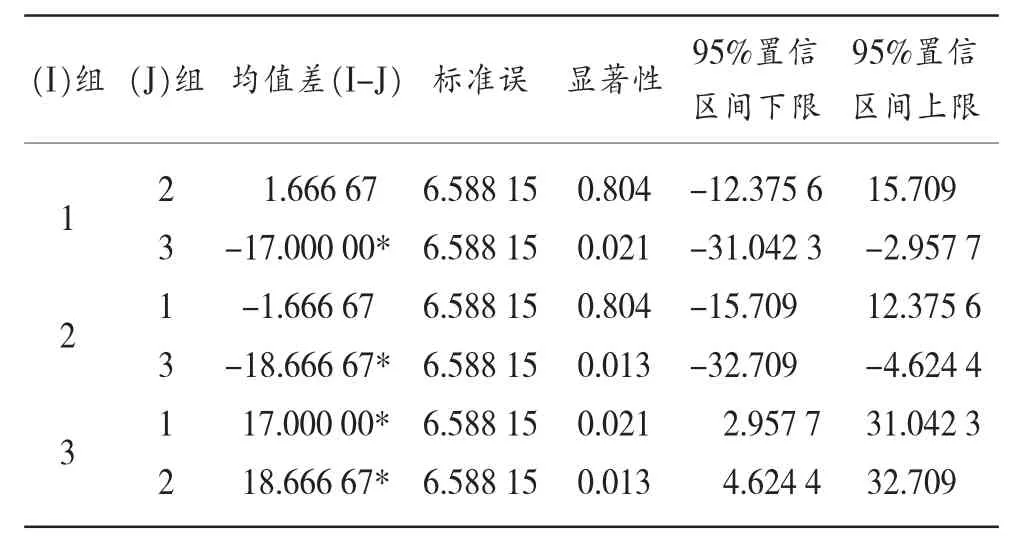
表3 方差分析表單因素方差分析的多重比較
由圖2可知,概率P值為0.023,小于顯著性水平0.05,所以接受H1,認為三種不同教學方案有明顯差異。
由圖3可進一步研究三種教學方案兩兩之間是否存在顯著性差異。
對比問題一和問題二,可以看出:ANOVA和T檢驗都是變異數分析(analysis of variance)的其中一種。而ANOVA可以看作是T檢驗的擴展。T檢驗適用于自變量只有兩個水平的均數的比較,而單因素方差分析適用于自變量有兩個或兩個以上的水平的均數比較。在此要說明的是,T檢驗的工作量很大,如果對同一組均數反復使用T檢驗,犯第一類錯誤的概率會上升。所以,一定不能在多組均數比較的時候貿然使用T檢驗,在多數情況下,方差分析更加合適,其優點是:將變異分類,從而能將變量的交互作用分離出來討論研究。
問題三:在問題二的基礎上,思考不同地區實施不同教學方案后學生的體育成績是否存在差異。即需要考慮這兩個自變量之間是否存在交互作用。單用T檢驗是不能解決這個問題的,在這個雙因素實驗中用方差分析來考察兩個自變量的交互作用。如果交互作用不顯著,則直接比較主要效果;如果交互作用顯著,說明一個變量對另一個變量有影響,直接比較主效應是沒有意義的,需進行單純主要效果的比較。結果如下:
由表4知,地區類型和教學方案這兩個自變量存在交互作用,需進行單純主要效果比較。由此可以看出方差分析與T檢驗的關系:當樣本數為2個時,方差檢驗結果與T檢驗一致。但方差可以同時檢驗所有自變量的均值。
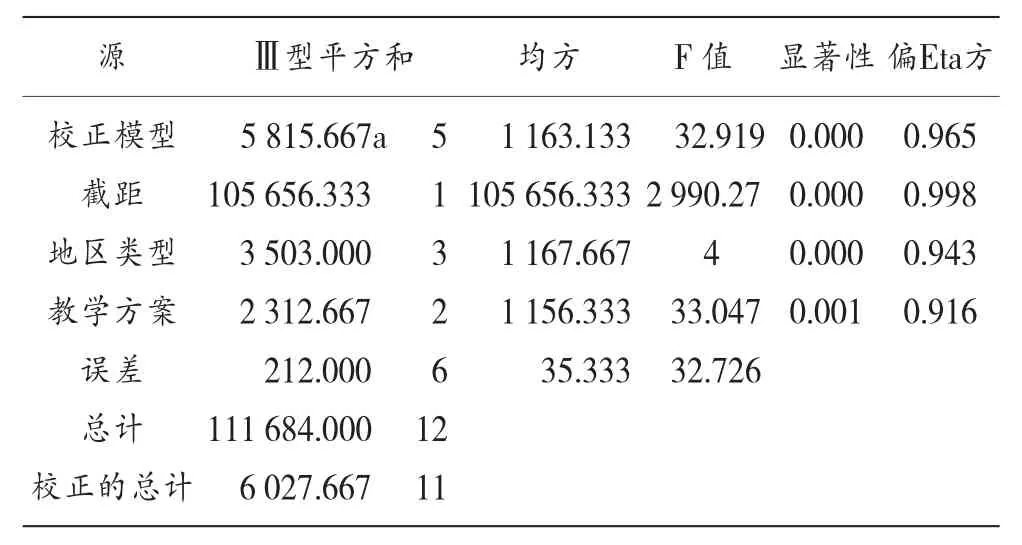
表4 方差分析表雙因素方差分析主體間效應的檢驗
問題四:研究學生體育成績和英語成績是否有相關關系。除了做均數比較還能做出哪些有效的統計推斷。從考慮自變量和因變量的相關入手,可以利用回歸分析得到自變量和因變量的線性關系。以下是采用相關分析得出的結果:
從表5中可以看出,學生體育成績和英語成績的相關系數為0.732,應被認為是中度相關,表明這兩門學科成績之間具有較密切的關系。從更嚴謹的角度,還要進行回歸分析,以提高分析結果的可靠性。基于回歸分析原理,我們把英語成績當成自變量,體育成績作為因變量,用SPSS得到回歸分析,結果如下:

表5 相關性檢驗結果相關性分析(Correlations)
表6可看出,統計量F=11.554,顯著性水平的P=0.007,說明因變量與自變量之間的線性關系明顯。從表7中可以看出估計值及其檢驗結果,常數項等于8.721,回歸系數為0.894,回歸系數檢驗統計量t=3.399,對應的置信水平為0.007,遠比常用的置信水平0.05要小,因此可認為該系數是顯著的,該回歸方程有統計意義:Y=8.721+0.894x。
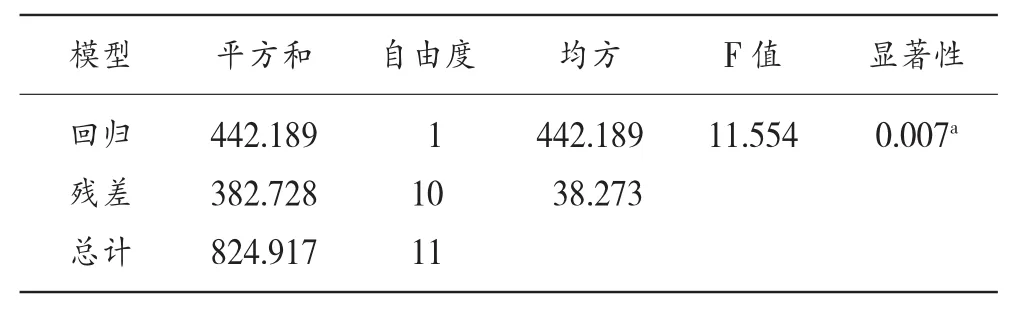
表6 方差分析表(ANOVAb)
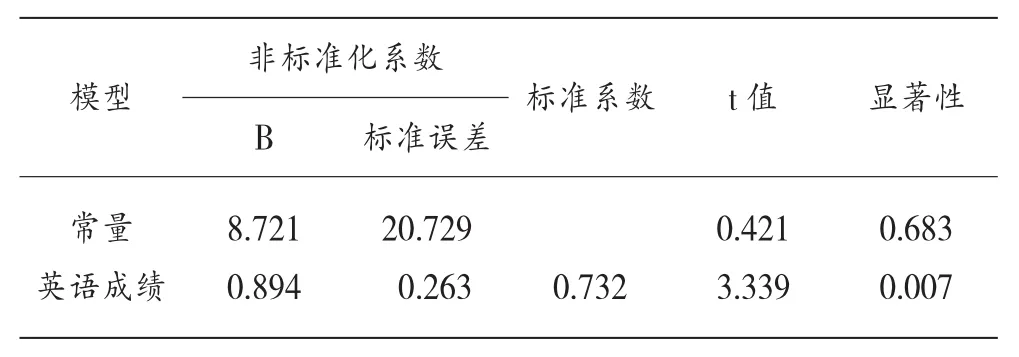
表7 回歸系數表回歸方程系數(Coefficientsa)
綜上可見,回歸分析與方差分析的共同點都是研究變量之間關系。不同之處在于回歸分析著重在尋求變量之間近似的函數關系,方差分析著重考慮一個或一些變量對一特定變量是否有影響及影響大小。
3.3 從變異角度的比較研究
統計分析在很大程度上是分析數據的變異[6]。變異的性質和形式不同導致多種多樣統計推斷方法的產生。總體內個體之差異是造成抽樣誤差的直接原因,正因為抽樣誤差的存在,才需要統計描斷,總體情況不同,抽徉誤差的來源就不一樣,因而其估計量不同,相應的統計方法也就不同。
在T檢驗中,分析抽樣誤差來源于何種變異是正確運用T檢驗方法的關鍵。 例如,對于兩個正態總體 N(μ1,σ2)和N(μ2,σ2),其中參數均未知,欲推斷 μ1和 μ2有無顯著差異。 現從兩個總體中分別抽樣,得到兩個樣本觀測值(x1,x2,……xn)與(y1,y2,……ym),抽樣誤差來自兩個總體內部的個體差異,這就是常用的獨立樣本T檢驗。
方差分析中是將總變異按指定來源分解為若干變異之和,并以組間變異和組內變異來衡量條件因素和隨機因素的影響大小,從而通過比較組間方差和組內方差以檢驗條件因素的作用是否顯著,方差分析本身就是分解變異的一種技巧。自變量固定一個值的時候,因變量不能確定 (存在變異),這才需要回歸分析。
回歸分析與方差分析都是檢驗線性模型。回歸分析中的回歸系數γ2=(SSY-SSresidua)/SSY,它代表因變量y所有的變異中由自變量x造成的變異所占的比例。方差分析中F=(SSBGdfWB)/(dfGBSSWB),F值則表示組內效應與分組效應的比值,兩者都用離差平方和表示。方差分析與T檢驗僅僅是對均數進行比較,回歸則考慮自變量和因變量之間的關系。因此,從某種角度上來說,方差分析是回歸分析的特例。
4 結論與建議
綜上所述,體育模型經典參數檢驗方法之間存在著一定形式的聯系。T檢驗和方差分析是進行均數比較的重要手段,而回歸分析在處理各種復雜變量關系的時候會有更多的解釋力。鑒于體育統計學在體育科學化發展中的重要作用,提高我國廣大體育科研工作者的體育統計應用水平是當務之急。無論是統計理論的學習和理解,還是統計思想和方法的應用,根據使用范圍和前提假設選用正確的模型統計檢驗方法是提高體育統計應用水平的關鍵。相似的檢驗方法之間在應用中需要判別檢驗效率的高低,這些都是需進一步研究的議題。
[1]盧紋岱,朱紅兵,何麗娟,等.統計軟件應用的常見誤區與解決途徑[J].首都體育學院學報,2005(1).
[2]魏登云.提高體育統計應用水平的關鍵正確認識統計總體[J].體育科學,1997(2).
[3]高 亮.比較體育教學方法效果研究的假設檢驗問題[J].湖北體育科技,2002(1).
[4]鄭春玲.淺談假設檢驗在體育統計中的應用[J].景德鎮高專學報,2006(2).
[5]劉厚生.回歸分析方法在體育科研中的應用初探[J].體育科學,1993(3).
[6]魏登云.體育統計中幾個重要概念[J].安徽體育科技,2008(4).

