基于第一扇區坐標分量的SVPWM快速算法

榮 飛 董興發

(1.山西同煤集團煤峪口礦，山西 大同 037000； 2.太原理工大學機械工程學院，太原 030000)

空間矢量脈寬調制(Space Vector Pulse Width Modulation，SVPWM)技術是一種比SPWM技術更為先進的、計算機可高度介入的脈沖寬度調制(Pulse Width Modulation，PWM)方法。它具有諧波含量少、開關損耗小和直流電壓利用率高的優點，且磁鏈軌跡更逼近圓形，轉矩平穩，因此得到了日益廣泛的應用[1]。傳統的SVPWM算法涉及到大量的運算，主要是三角函數運算和矩陣運算，這大大增加了控制器的負擔和程序占用的存儲空間[2]。

筆者提出了一種新型的SVPWM快速算法，該算法能根據參考矢量的坐標分量迅速判斷出參考矢量所在的扇區，且僅需根據坐標分量計算出第一扇區的時間，即可求出其他相關矢量的作用時間，易于數字化應用，具有很好的實用性。

1 SVPWM快速算法①

1.1 扇區判斷

兩電平在三坐標軸坐標系空間中的矢量圖如圖1所示，圖中的扇區號經過了順序調整，該操作的仿真模塊如圖2所示。

圖1 兩電平三坐標軸坐標系中的矢量圖

Ux，Uy，Uz——參考矢量在坐標系的分量；

V1～V6——兩電平空間矢量圖的基本向量；

Vref——參考矢量

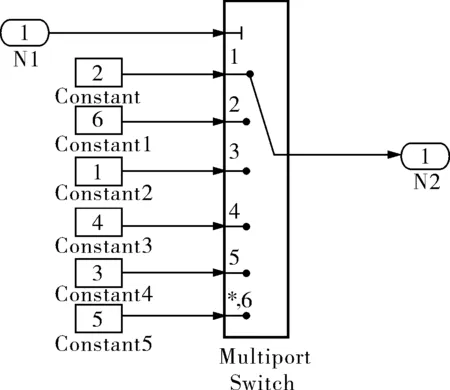
圖2 扇區調整仿真模塊

如圖1所示，在兩電平電壓空間矢量圖中建立一個與所有扇區嚴格坐標系，其中3個坐標軸x，y，z分別位于扇區Ⅰ，Ⅱ，Ⅲ的角平分線上。設參考矢量在坐標系的分量分別為Ux，Uy，Uz[3]，即：

(1)

若Uz>0，則扇區可能為Ⅱ，Ⅲ，Ⅳ；Uy<0，則扇區可能為Ⅳ，Ⅴ，Ⅵ,因此若Uz>0且Uy<0，則參考矢量所在的扇區為Ⅳ，于是得出參考矢量所在扇區的判斷關系見表1[4]。

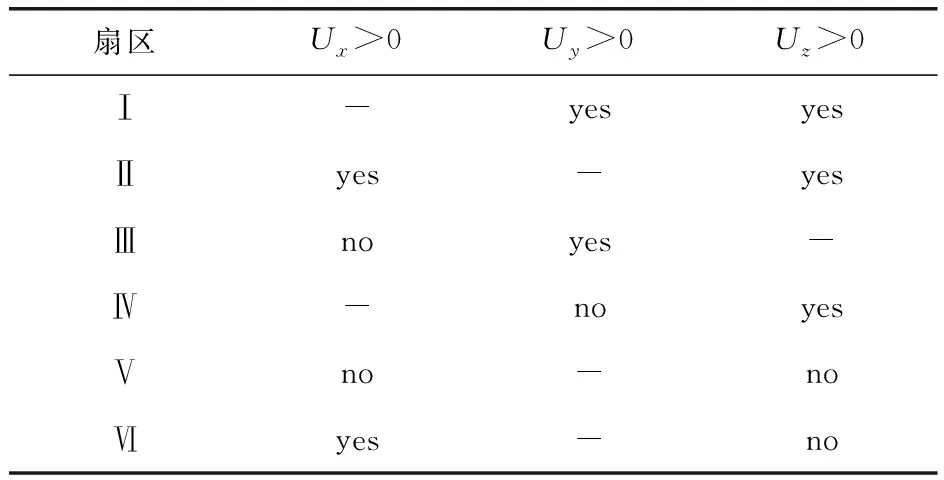
表1 扇區判斷關系表

1.2 相關矢量作用時間計算

相關矢量作用時間的計算依據的是矢量的平行四邊形定則，因此若合成兩個不同參考矢量的平行四邊形是全等的，則它們的相關矢量作用時間要么相同要么順序相反。

如圖3所示，若參考矢量Vref在第二扇區與第一扇區內的模長相等，且第二扇區的參考矢量經角度變換轉化到第一扇區后，與α軸正向的夾角與第一扇區的參考矢量和與α軸正向夾角相等。則這兩個平行四邊形是全等的。圖3中，T11、T12、T21、T22為與參考矢量相關的基本矢量的作用時間，于是得T11=T22,T12=T21。當參考矢量位于第三扇區時，同理可得其作用時間與第一扇區作用時間的對應關系為T31=T11,T32=T12。這樣就可以用第一扇區的時間來代替其他扇區的時間。

圖3 扇區Ⅱ，Ⅰ作用時間關系

設Vref位于第一扇區，由傳統的SVPWM算法可得矢量的作用時間為[5]：

(2)

與式(1)相比較得：

(3)

得到的各扇區的矢量作用時間見表2。

表2 各扇區矢量作用時間

于是將參考矢量旋轉到第一扇區后，就可以用式(3)來求所有扇區相關矢量的作用時間了，參考矢量轉化公式為:

theta=θ-π(N-1)/3

(4)

式中N——扇區數；

θ——參考矢量與α軸正方向的夾角[6]。

2 仿真驗證

在Simulink中建立了該算法和傳統算法的仿真模型。直流電壓設為600V,仿真時間為0.7s，異步電動機參數設置為：額定功率4kW,線電壓有效值400V,頻率50Hz，二對極RS=1.405Ω，LS=0.005 839H,Rr=1.395Ω，Lr=0.005 839H，Lm=0.172 2H,轉動慣量為0.013 1kg·m2，機械負載轉矩為30N·m。圖4、5分別為逆變器在該算法下輸出的相電壓波形圖和線電壓波形圖(橫軸單位為s，縱軸單位為V)，由輸出波形可知該算法是正確的。圖6為電機轉矩曲線，圖7為電機轉速曲線，由電機輸出的曲線可知，該算法有較好的穩定性。

圖4 相電壓波形

圖6 電機轉矩曲線

3 結束語

筆者提出了一種基于第一扇區坐標分量的SVPWM算法，簡化了扇區判斷及相關矢量作用時間的計算量，提高了系統的實時性，系統達到穩態后，運行平穩，且該方法具有很好的實用性。

圖7 電機轉速曲線