基于TC控制與干擾觀測器的Smith預估控制

李 光 鄭恩讓

(陜西科技大學電氣與信息工程學院，西安 710021)

工業過程中滯后現象的存在對系統的穩定性和動態品質影響非常大，會使系統的超調量增大，響應時間變長，更有甚者會使系統出現振蕩、發散的情況，導致系統的控制效果降低。瑞典科學家Smith于1957年提出的Smith預估器從理論上解決了時滯對系統的影響，但是需要知道對象的精確數學模型，而且只能用于定常系統，所以在實際應用中受到限制。另外該方法還存在魯棒性差和抗擾性差的問題，因此許多文獻都提出了擴展型或改進型的方法：文獻[1～6]把自抗擾技術與Smith預估器相結合；文獻[7]通過重復控制的方法對控制器參數進行了自整定；文獻[8，9]對Smith預估器做了修改，增強了抗擾性。

筆者對傳統的Smith預估器也進行了兩方面的改進：首先采用一種控制結構簡單、不需要精確模型、動態響應速度可調且易于實現的魯棒控制器(TC控制器)；其次，加入了干擾觀測器，增強了系統的抗擾性。通過對典型時滯系統的大量仿真，結果表明：當數學模型參數τm變化50%時，系統輸出仍然平滑而且響應速度快，驗證了該方法對于穩定時滯系統的有效性和可行性。

1 改進型Smith預估控制①

為了提高傳統Smith預估控制器的魯棒性和抗擾性，使用TC控制器代替PID控制器，并且加入了干擾觀測器，系統的結構如圖1所示，當被控對象與數學模型完全匹配時系統的閉環傳遞函數為：

(1)

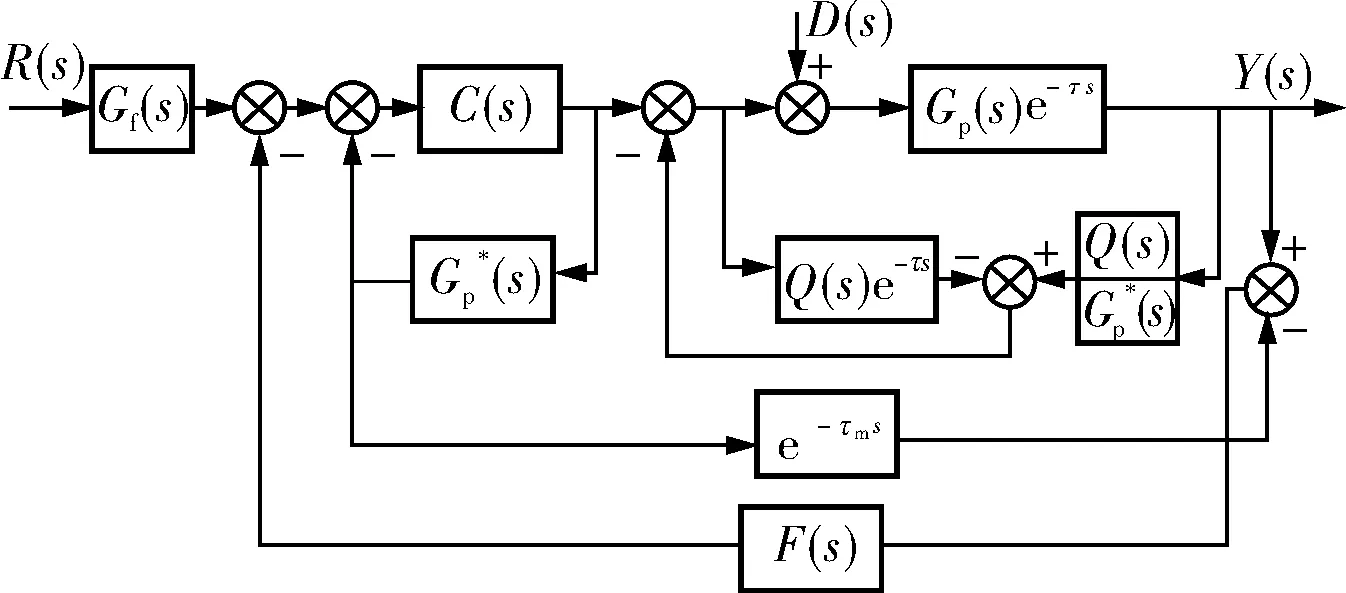
圖1 改進型Smith預估控制器框圖

1.1 TC控制器

1992年，意大利學者Tornambè A和Valigi P提出了TC控制器[10]，其核心在于構造觀測器獲得對擾動的估計和補償以提高控制效果，該方法控制結構簡單，不需要精確模型，易于在工業過程中實現。系統的相對階數為一時，TC控制律為[11]：

(2)

h0——可調預期動力學參數，決定系統的響應速度；

k0——可調參數，決定系統的魯棒性；

y——系統輸出；

yr——系統給定；

ξ——中間變量。

1.2 穩定時滯系統控制器設計

考慮如下形式的一階穩定時滯系統：

(3)

由式(2)得到TC控制器的表達式：

(4)

a=h0+k0,b=h0k0

(5)

E(s)=Yr(s)-Y(s)

(6)

把式(3)、(4)代入式(1)，得到閉環傳遞函數：

(7)

筆者按照文獻[12]的ITAE控制系統優化設計方法來進行參數整定。將特征多項式Ts3+s2+aKs+bK的系數與基于ITAE指標的Φ(s)的最優系數進行對比，求解得到參數a、b的表達式：

(8)

(9)

其中ωn是系統自然頻率。

按照上述方法也可以得到二階穩定時滯系統的參數表達式：

(10)

(11)

(12)

2 干擾觀測器

干擾觀測器的基本設計思想是將外部力矩干擾和模型參數變化造成的實際對象與名義模型輸出的差異統統等效為控制輸入端，即觀測出等效干擾，在控制中引入等量的補償，實現對干擾完全抑制。干擾觀測器的原理如圖2所示。

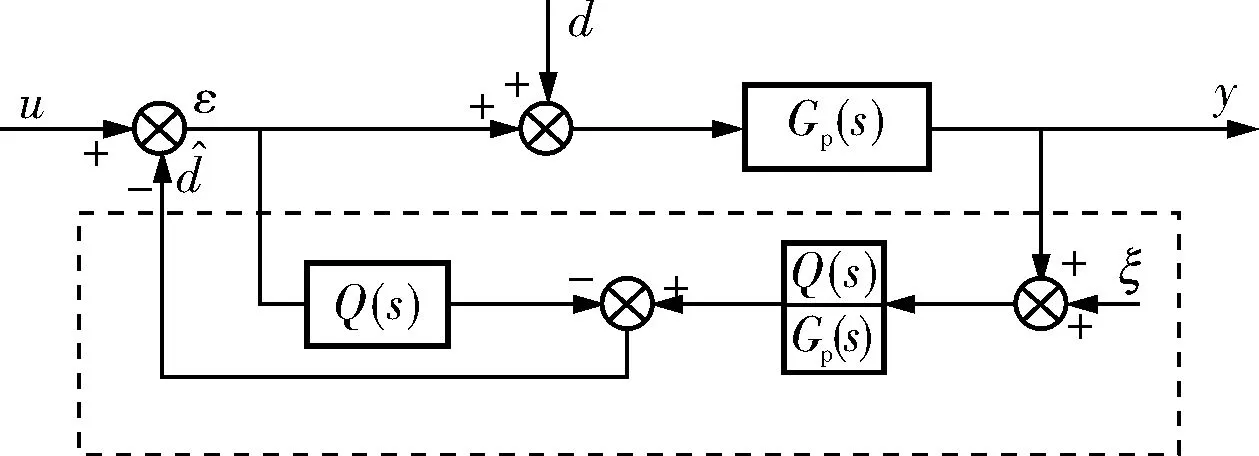
圖2 干擾觀測器原理框圖

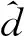
(13)

由圖1可得到擾動輸入的傳遞函數：

Yd(s)=Gp(s)[1-Q(s)e-τs]e-τsD(s)

(14)

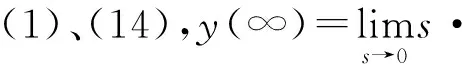
Q(s)的設計是干擾觀測器設計中一個非常重要的環節。首先，為使Q(s)Gp-1正則，Q(s)的相對階應不小于Gp-1的相對階；其次，Q(s)寬帶的設計是在干擾觀測器的魯棒穩定性和干擾抑制能力之間的折中[13]。

設Gp(s)的名義模型為Gn(s)，則不確定對象的集合可以用乘積攝動來描述，即：

Gp(s)=Gn(s)[1+Δ(s)]

(15)

式中Δ(s)——高頻振動。

由魯棒穩定性定理可知，低通濾波器Q(s)魯棒穩定的充分必要條件：

(16)

當被控對象與數學模型失配時,被控對象與預估器模型的誤差為：

(17)

考慮只有τm變化時,對式(17)通過泰勒級數展開：

Df(s)=Gp(s)[0.5(τ-τm)s2-(τ-τm)s]F(s)

考慮一階時滯對象：

(18)

(19)

這樣通過設計濾波器F(s)就可以減小模型失配時的誤差。

3 仿真研究

為驗證筆者提出的改進型Smith預估控制方法，以下用該方法和文獻[14]中的方法對工業過程中典型的一階和二階穩定時滯系統進行仿真研究。

3.1 一階穩定時滯系統仿真

考慮如下一階穩定時滯系統：

(20)

根據文獻[14]中的方法，選取PI控制器的參數為Kp=0.037 5,Ti=3。根據式(5)、(8)，選取TC控制器參數為h0=17.3,k0=2.7，濾波器Q(s)=1/(3s+1)，F(s)=1/(150s+1)。

在模型匹配時，為驗證系統的跟蹤性能和抗擾性，分別在t為1、100s時輸入單位階躍信號和0.2的階躍干擾信號，響應曲線如圖3所示。

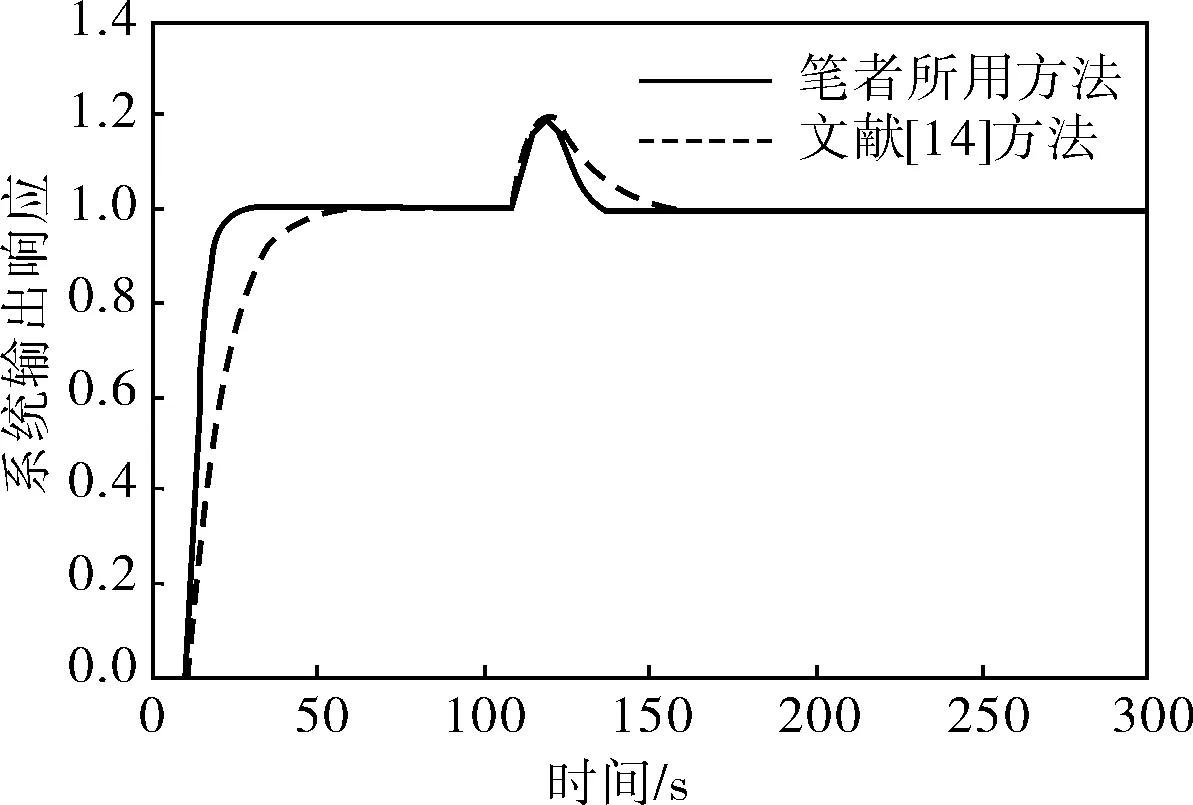
圖3 一階對象模型匹配時系統的響應曲線

在模型失配時，為驗證系統的魯棒性和抗擾性，使數學模型參數τm變化50%時的響應曲線如圖4、5所示。

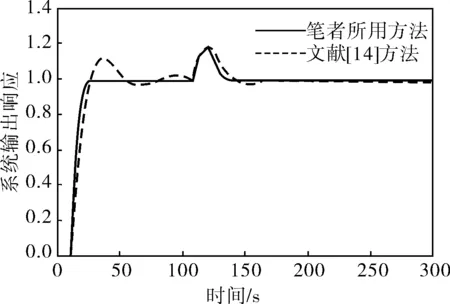
圖4 一階對象模型τm減小50%時的響應曲線

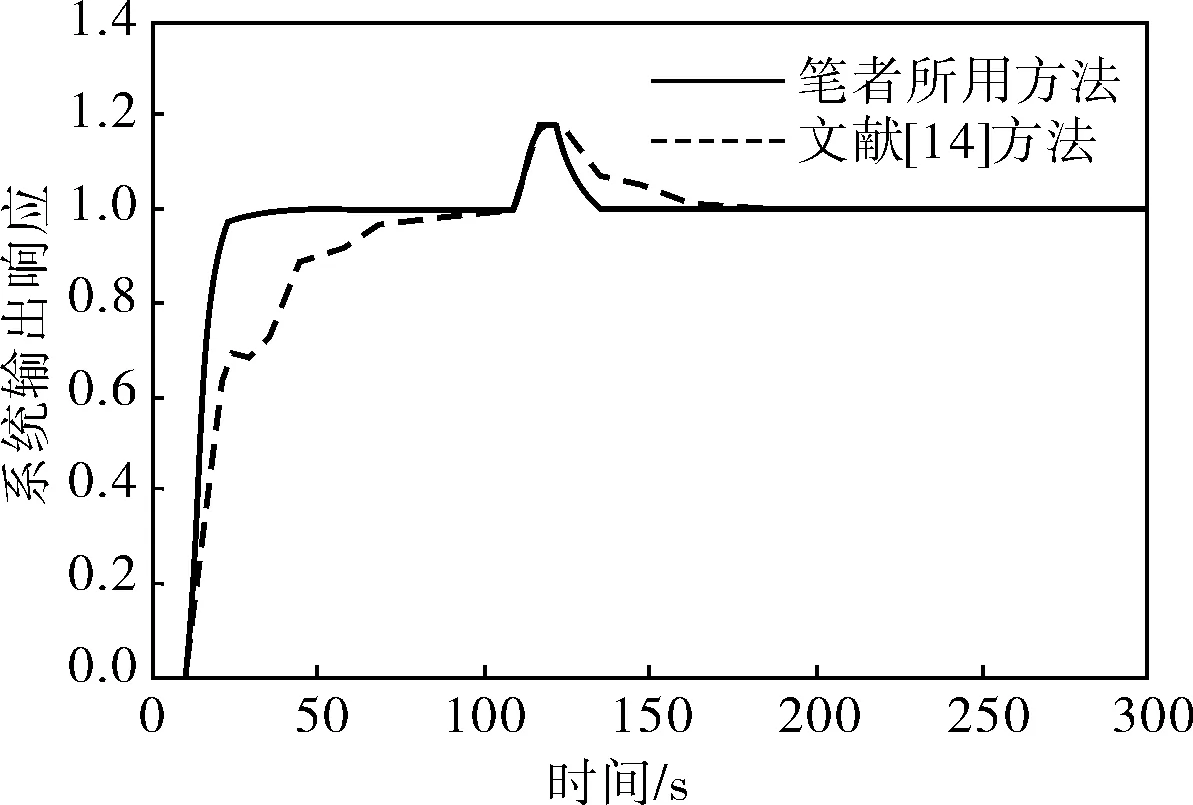
圖5 一階對象模型τm增大50%時的響應曲線

從圖4、5可以看出，雖然預估器模型的純滯后時間變化幅度大，但該方法仍然可以很好地控制系統，在一定程度上不存在所謂的模型失配問題。

3.2 二階穩定時滯系統仿真

考慮如下二階穩定時滯系統：

(21)

按照3.1節所述，選取PID控制器的參數為Kp=0.05,Ti=5,Td=6/5。TC控制器的參數為h0=102,k0=0.5，濾波器Q(s)=1/(3s+1)2，F(s)=1/(150s+1)。

在模型匹配時，在t分別為1、100s時輸入單位階躍信號和0.2的階躍干擾信號，響應曲線如圖6所示。

圖6 二階對象模型匹配時系統的響應曲線

在模型失配時，模型參數τm變化±50%時的響應曲線如圖7、8所示。

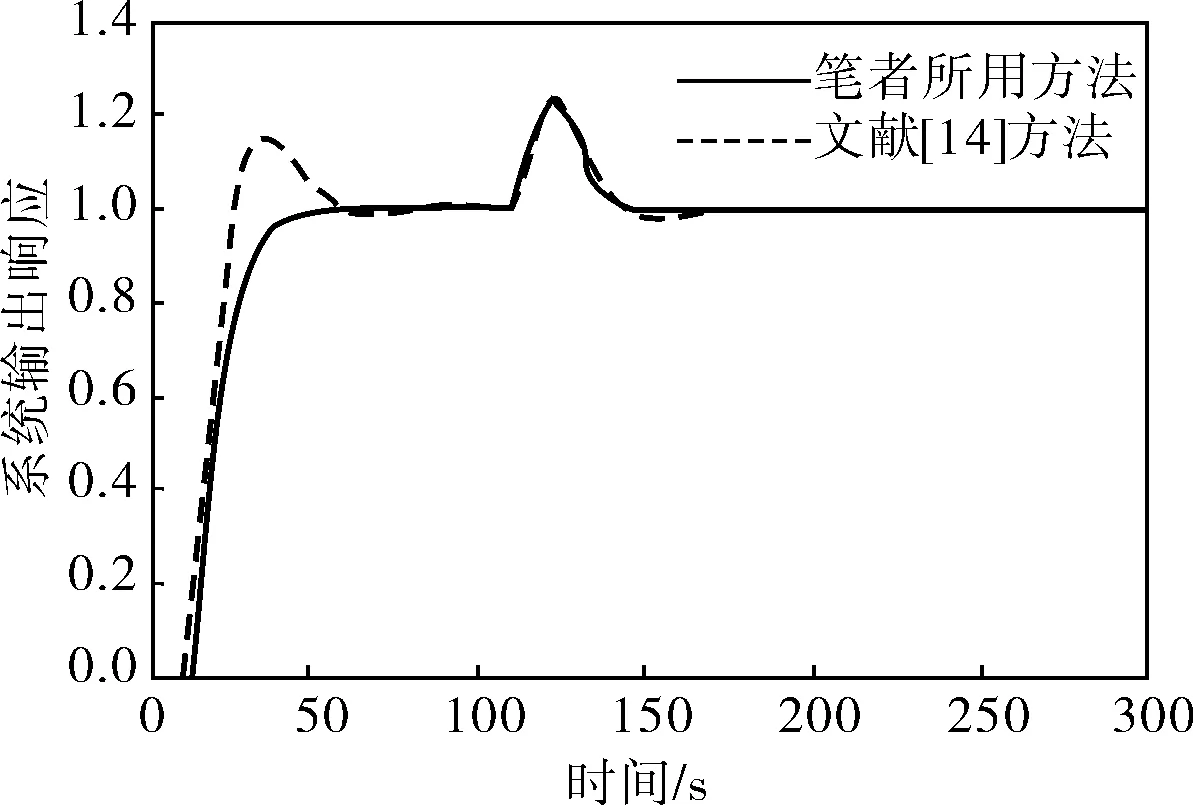
圖7 二階對象模型τm減小50%時的響應曲線

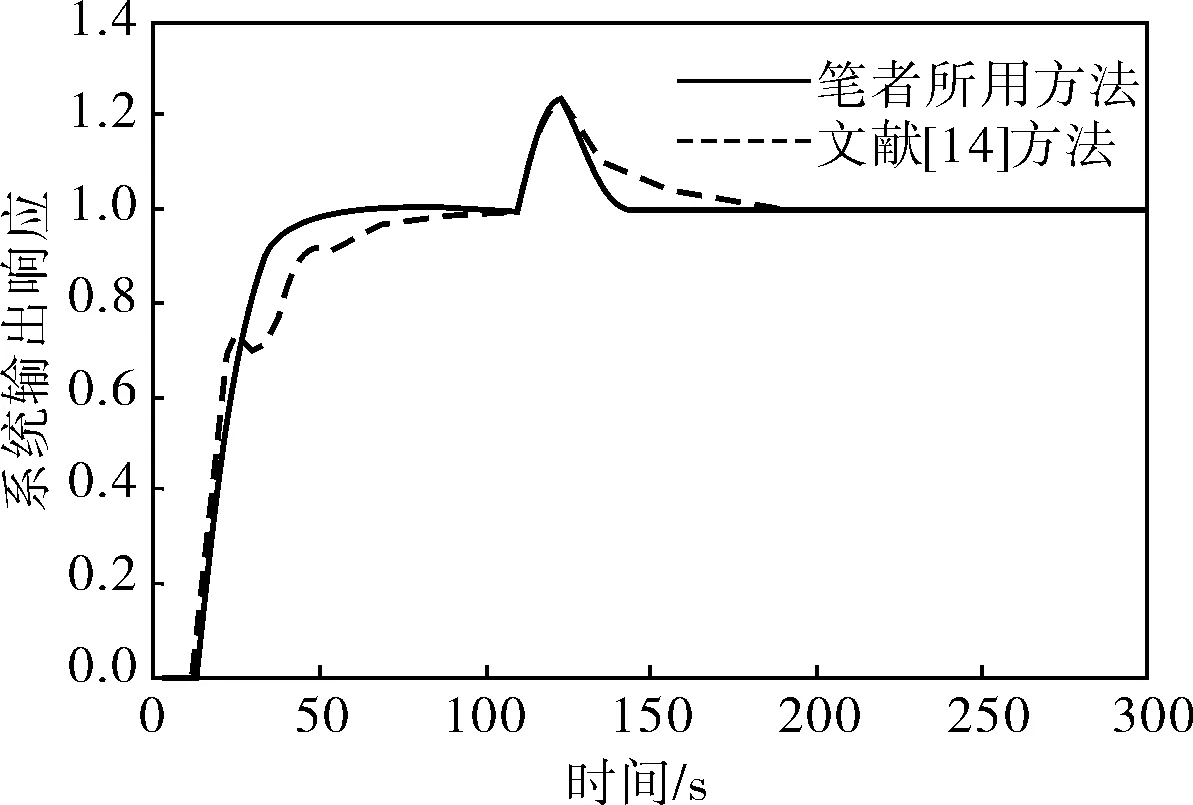
圖8 二階對象模型τm增大50%時的響應曲線

同理，從圖7、8可以看出，筆者所述方法仍然可以有效地控制二階穩定時滯系統。

由仿真結果可知，模型參數變化±50%時，筆者所述方法的系統輸出仍然平滑而且響應速度快，克服了傳統Smith預估器魯棒性差和抗擾性差的缺點，提高了控制系統的品質。

4 結束語

傳統Smith預估控制在實際中控制效果不佳，模型失配時魯棒性和抗擾性差。針對這兩方面提出了一種不依賴于精確數學模型、結構簡單、響應速度快、易于實現的TC控制器與干擾觀測器相結合的改進型Smith預估器。通過對典型穩定時滯系統的大量仿真研究，可以發現該方法克服了傳統Smith預估器的缺點，明顯地改善了控制系統的品質。