針對不穩定對象的改進動態矩陣控制

張 誠 佃松宜

(1.四川建筑職業技術學院，四川 德陽 618000；2.四川大學，成都 610065)

20世紀70年代中期，動態矩陣控制(Dynamic Matrix Control，DMC)就應用在美國殼牌石油公司的生產裝置上[1,2]。1979年，Cutler C R和Ramaker B L在美國化工年會上首次介紹了這一算法[3]。幾十年來，動態矩陣控制在參數優化、多變量系統和與智能控制相結合方面有很大的發展[4,5]。目前，動態矩陣控制在工業控制領域中獲得了大量成功的應用[6,7]。由于動態矩陣控制算法是基于線性對象的有限階躍響應的非參數模型，所以它只適用于漸近穩定的線性對象，不能直接用于不穩定的被控對象。對于不穩定對象的動態矩陣控制研究，席裕庚提出將傳統PID控制與動態矩陣控制相結合的控制策略[1]；孫欣等提出將動態矩陣控制與狀態反饋結合起來的控制策略[8]。針對這一問題，筆者基于傳遞函數互質分解的現代頻域法，提出一種新的改進動態矩陣控制策略。

1 控制系統設計①

筆者提出的改進動態矩陣控制的結構如圖1所示。采用現代頻域法中的互質分解法設計內環控制器D[9]，得到穩定的廣義對象，然后再針對廣義對象進行動態矩陣控制設計。這樣做的好處是不僅可以得到保證內環穩定的所有控制器D，而且還可以利用頻域優化理論來優化內環控制器，使內環的抗擾性和魯棒性達到最優。也就是說，如果能夠最大限度地改善內環的抗擾性，并將內環對受控對象模型失配的敏感度降到最低，就間接地改善了整個DMC系統的抗擾性和魯棒性。利用內環控制器可調節系統的抗擾性和魯棒性，并通過H2理論優化系統的動態性能[10]。

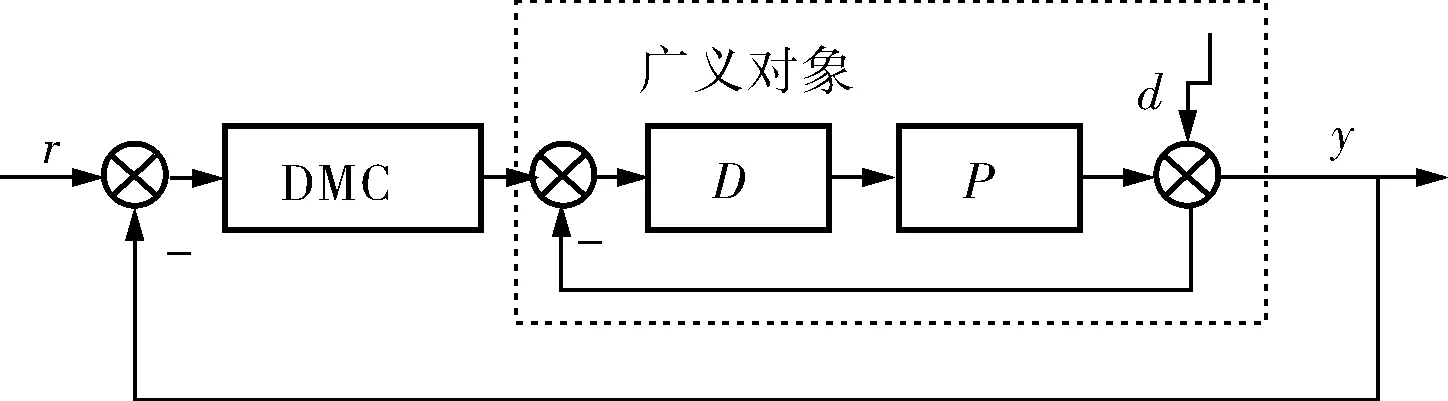
圖1 控制系統結構

1.1 內環控制器D的設計

采用現代頻域法的互質分解法來對控制器D進行設計[11]。將對象P分解為：

(1)

輸入r分解為：

(2)

擾動d分解為：

(3)

其中nP、dP、d1、dd1、dr1、αr、αd∈H∞，dr1、dd1為單模函數，αr、αd的零點全在不穩定域，設αc為αr和αd的最小公倍式，則可以得到所有保證閉環系統穩定和穩態無差的控制器D：

(4)

其中q為自由參數；xP、yP滿足Bezout等式nPxP+αcdPyP=1。

當系統沒有模型失配時，將干擾d到輸出y的傳遞函數定義為敏感性函數，代表干擾對輸出的影響。當系統存在模型失配時，敏感性函數同時也是閉環傳遞函數的相對誤差與對象模型的相對誤差之比，反映模型失配對系統的影響。因此控制系統的敏感性函數為：

(5)

采用H2優化方法來優化敏感性函數，使擾動和模型給系統帶來的影響最小。

當擾動未知時，取性能指標為J=‖W1S‖2，其中W1為加權函數，W1∈H2，反映擾動d或對象模型失配的頻譜。當擾動已知時，可取性能指標為J=‖Sd‖2。因為D是基于互質分解方法設計的，將式(4)代入式(5)得：

S=αc(yp-qnp)dp

(6)

求出使J最小的q就可以得到抗擾性能和魯棒性能最優的控制器D。

1.2 動態矩陣控制算法

動態矩陣控制是一種基于模型預測、滾動優化和反饋校正的控制算法[1]，通過以下3個步驟實現：

a. 得到穩定的廣義對象后，對該對象進行單位階躍響應實驗，適當截斷階躍響應曲線得到階躍響應采樣序列a=[a1,a2,…,aN]T，得到未來P個時刻的輸出預測值yM(k)=y0(k)+A×ΔuM(k)，其中A是系統單位階躍響應系數陣；

b. 利用實際輸出和預測輸出的誤差e(k+1)來修正預測值；

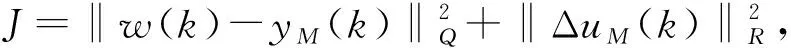
2 設計舉例與仿真結果

其中ε越小越接近最優解。

對廣義對象做階躍響應實驗，在t=9s時截斷曲線，響應值誤差范圍為±0.005，取N(N=30)個采樣值。預測時域p=10，控制時域M=2，誤差加權系數q=1，控制增量加權系數r=2，反饋校正系數h=0.01，根據DMC算法，得到最優控制。

在t=10s時加入幅值為0.2的階躍擾動，圖2是本文方法在參數ε取不同值時的仿真結果。

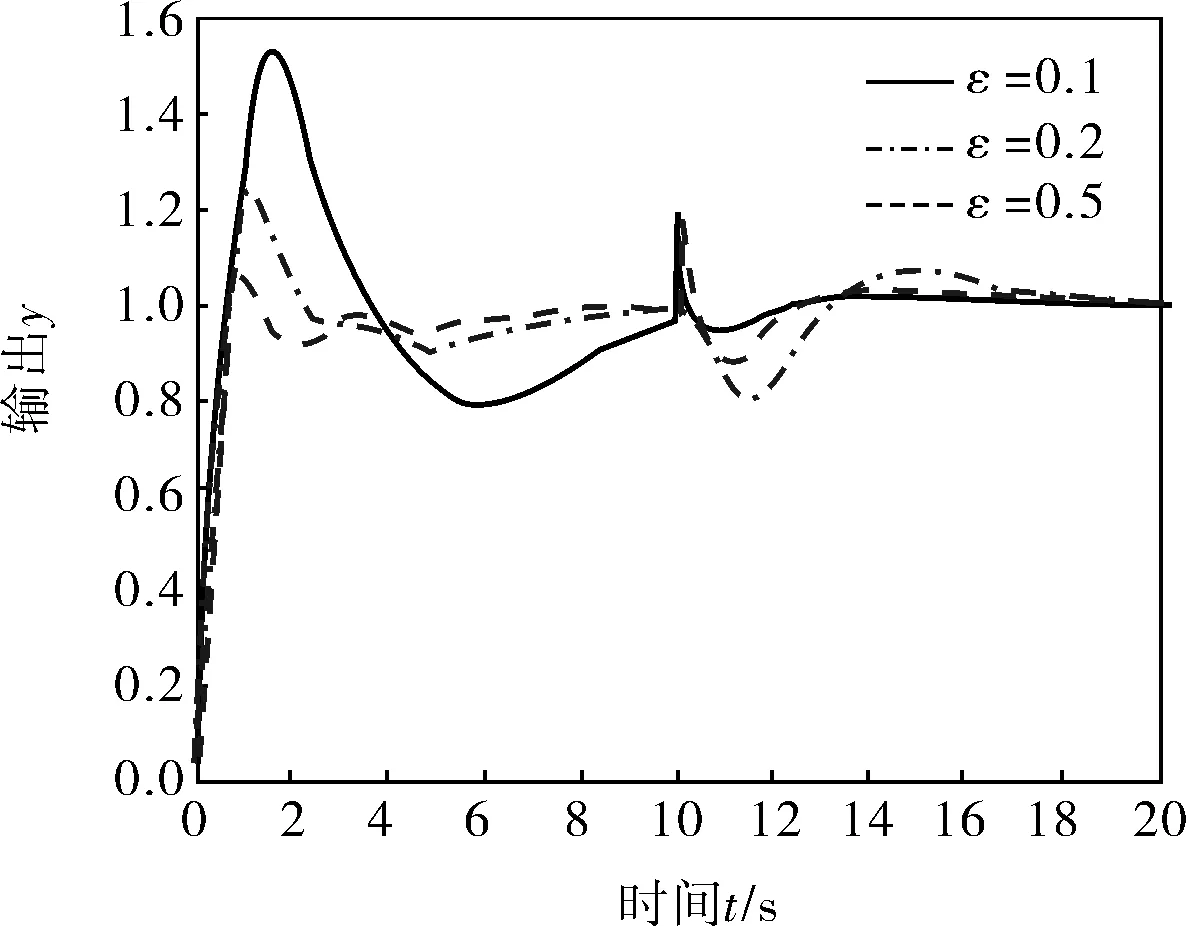
圖2 ε取不同值的仿真結果

由圖2可以看出，ε越小，響應越平滑，響應速度越快，超調越小，抑制干擾，能力越強。

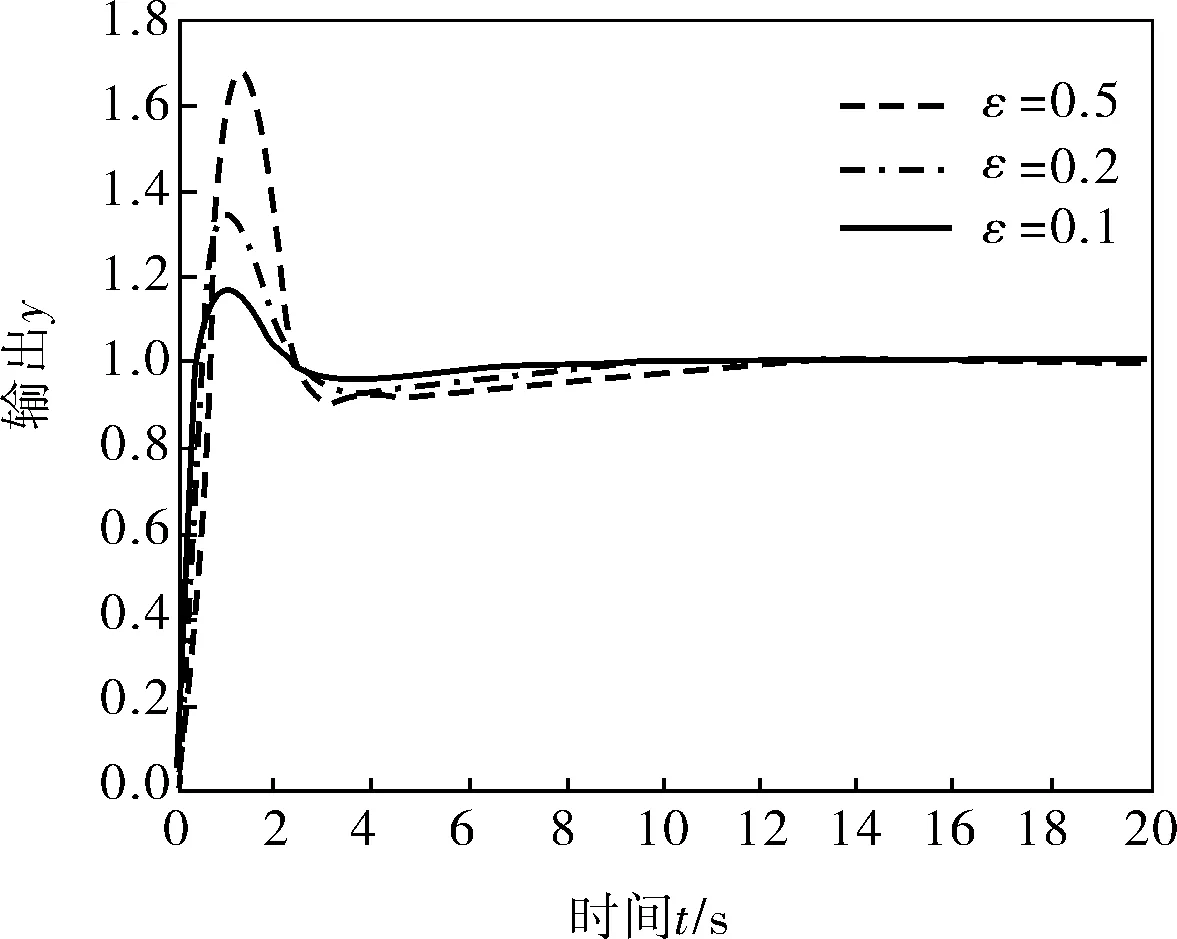
圖3 有模型失配時ε取不同值的仿真結果

由圖3可以看出，ε越小，系統的魯棒性越好。

文獻[8]通過設計狀態反饋增益陣使閉環系統穩定，根據LQR設計狀態反饋陣，再根據此穩定對象進行DMC設計。為比較本文方法與該方法，在t=15s加入幅值為0.2的階躍擾動且系統存在相同的模型失配，設置相同的DMC參數，仿真結果如圖4所示。可以看出，本文方法有更好的抗擾性和魯棒性。

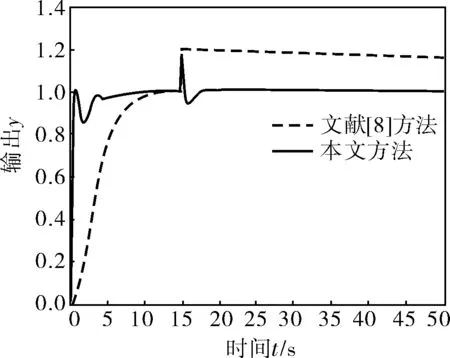
圖4 本文方法與文獻[8]方法的比較

3 結束語

筆者采用基于傳遞函數互質分解的現代頻域法，提出了先利用內環控制器D穩定對象，再對穩定后的廣義對象進行動態矩陣控制設計的方法，不僅能消除不穩定因素對系統的影響，而且能有效地改善系統的抗擾性和魯棒性。對工業上常見的含有不穩定環節的系統，本文方法可以有很好的控制效果。