基于柵格數據的局部奇異性分析迭代方法及其軟件實現
,,3,
(1.中國地質大學地質過程與礦產資源國家重點實驗室,湖北武漢430074; 2.中國地質大學(武漢)資源學院,湖北武漢430074; 3.York大學地球空間科學系和地理系,加拿大多倫多M3J1P3)
基于柵格數據的局部奇異性分析迭代方法及其軟件實現
陳志軍1,2,成秋明1,2,3,陳建國1,2
(1.中國地質大學地質過程與礦產資源國家重點實驗室,湖北武漢430074; 2.中國地質大學(武漢)資源學院,湖北武漢430074; 3.York大學地球空間科學系和地理系,加拿大多倫多M3J1P3)
近些年,弱緩化探異常識別已成為成礦預測和勘查評價中十分關鍵的問題。多重分形理論的局部奇異性分析因其嶄新的思路、簡便的方法、優良的效果而在弱緩異常識別中受到廣泛關注。在深入剖析局部奇異性分析基本思想及計算方法的基礎上,引入正規化尺度參數L,提出了迭代方法來改進局部奇異性指數的估值。給出了奇異性迭代算法并用C++編程實現,軟件功能強勁,操作靈活,不僅適用于各向同性情形,還適用于各向異性尺度的奇異性計算和方向性奇異性計算。軟件的動態鏈接庫版本已在GeoDAS礦產資源定量預測專業軟件中應用。
局部奇異性分析; 柵格數據; 多重分形; 迭代方法; 正規化尺度參數
0 引 言
分形與多重分形在勘查地球化學數據、勘查地球物理數據、礦石品位數據等地質勘查數據中的普遍存在性為成礦過程奇異性與礦產預測定量化的新理論與新方法研究提供了嶄新的思路和新型的數學工具(成秋明, 2007; Agterberg, 2003)。不均勻性、自相似性(自放射性、廣義自相似性)、奇異性等通常被用來描述地球化學場特征、礦床空間分布、熱液成礦系統礦床品位-噸位分形模型的非線性性質。一種五參數的多重級聯模型最近被提出,該模型對de Wijs’s鋅數據等多重分形經典數據的非對稱奇異譜進行了成功建模,為現實世界中地球化學場多重分形性的存在性提供了理論依據。分形維數、多重分形對稱度、多重分形奇異譜等參數從非線性角度對描述成礦物質富集與貧化的統計規律發揮了重要作用(成秋明, 2000, 2007),然而,對于礦產資源定量預測中的“定位”(礦產資源空間分布位置)預測功能則有所不足,需要將全局性統計轉變為局部化模型。基于多重分形理論建立的局部奇異性分析模型,試圖通過局部異常的有效識別來達到空間預測目的,該模型正逐漸在覆蓋區勘查地球化學弱緩異常識別中表現出巨大的應用潛力,成為非線性礦產預測的有效方法之一(成秋明, 2012)。應用的需求也促進了局部奇異性分析自身模型的發展,出現了多種形式的擴展模型(陳志軍, 2007)。主要從提高奇異性指數計算精度方面介紹局部奇異性分析迭代分析方法,設計算法并編程實現,同時指明準確計算奇異性指數需要注意的一些關鍵參數設置。
1 局部奇異性分析方法的基本思想
奇異性理論指出:奇異性是指在很小的時間-空間范圍內具有巨大能量釋放或巨量物質形成的現象(成秋明, 2006; Cheng et al, 2009)。假定在E維(拓撲)空間中有一由質點凝聚成分維數為D的分形(如礦物的富集),L尺度上質點集合的質量M(L)與集合中質點的數目N(L)成正比,則該分形體的密度可表示為(陳颙等, 2005):
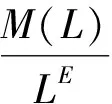
(1)
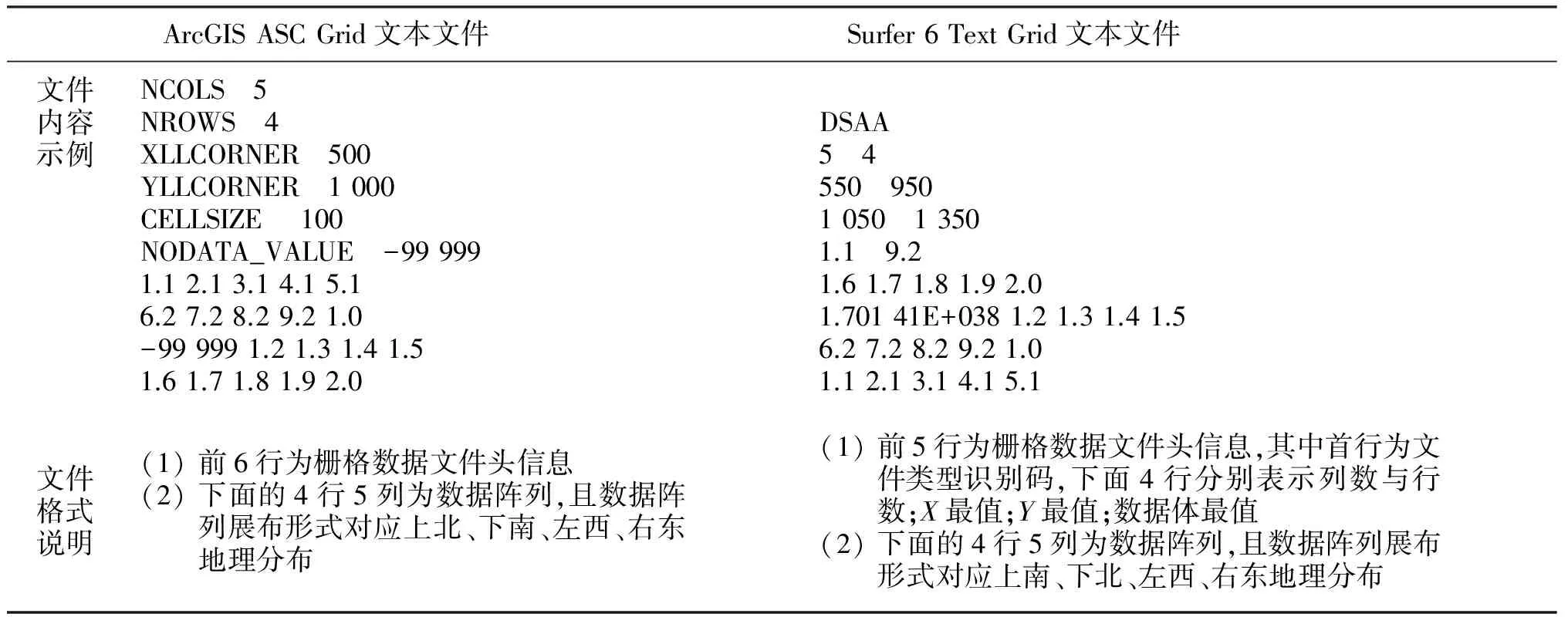
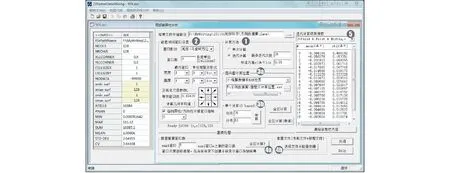
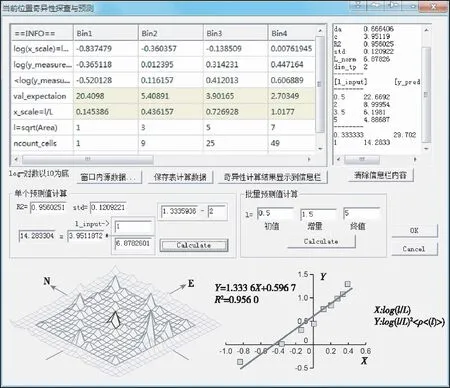
由式(1)可知,當D 該模型的基本內容:記B(x,ε)為任意空間位置x,尺度大小為ε的盒子(可以是方形、矩形、或其他更復雜的形狀),在盒子B(x,ε)覆蓋區域內的金屬量為μ(B(x,ε)),則有: μ(B(x,ε))=c(x,ε)εα(x) (2) 為便于理解與制圖,令: Δα(x) =E-α(x) (3) 設ε大小鄰域上的平均密度為〈ρ(B(x,ε))〉,〈〉表示統計期望,式(2)于是寫成密度形式,有: 〈ρ(B(x,ε))〉 =μ(B(x,ε)) /εE=c(x,ε)ε-Δα(x) (4) 式(4)中,E為研究對象的空間拓撲維數(E=1,2,3,分別對應一維、二維或三維問題),待定系數α(x)稱為空間位置x處的局部奇異性指數,它表征了奇異性的強弱程度,是與尺度無關的量,無量綱;若ε趨近于0且c(x,ε)存在,則此時的c值被認為是位置x處的“α(x)維分形密度”。若ε用最大尺度進行了歸一化,則c(x,ε)值是對該最大尺度的滑動平均的逼近。對地球化學采樣數據,測量所得數據通常表示的是濃度含量,可視為一種廣義的“密度”數據。因此,利用式(4)可直接對化探測量原始數據建模,對結果解釋更直觀,故而在分析中式(4)比式(3)更常用。需要注意的是,式(3)也是非常有用的,特別是在奇異性指數的算法設計方面。式(3)在計算中可直接獲得α值并且其擬合優度高于用式(4)直接獲得的Δα。這是由于普通最小二乘(OLS)模型只考慮縱向誤差,而α的均值水平趨近于E、Δα的均值水平常趨近于0的緣故。(-Δα)作為log-log坐標系中回歸直線的斜率,若其結果近似為0,意味著自變量和應變量不存在相關關系;同樣的數據用α來表示(此時近似為E),自變量和應變量的相關關系將變得顯著。無論用式(3)還是式(4)計算,獲得的奇異性指數和局部系數是一致的,不同的是log-log坐標系下對應的回歸方程具有不同的顯著性水平。要解決此問題,對式(4)和式(3)在log-log坐標系下可選用標準加權最小二乘法(SWLS),權重為1/(1+b2)(其中b為擬合直線斜率),以觀測點到回歸直線的垂直距離平方和最小化來確定直線參數,當然該計算過程比普通最小二乘模型略顯復雜。 奇異性指數α值(或Δα)有著優良的異常指示功能,在實際應用中常用來度量不同空間位置物質(或能量)較其周圍相對富集或虧損的程度。α值與E偏差越大,說明局部富集或虧損越越強烈,也即奇異性越強。以二維化探異常研究為例,此時E取值為2,當α<2(即Δα>0)表示局部正異常,元素相對局部富集;α>2(即Δα<0)表示局部負異常,元素相對局部虧損;而α= 2(即Δα=0)表示無異常,屬于背景。通常在全圖范圍內計算各個位置的α值,對α值(或Δα值)進行制圖表達,從而來識別不同空間位置的局部化探異常,并進一步篩選出有用異常并在空間上圈定出來。沒有奇異性的區域(α=E)所構成子集的分形維數接近于分形盒維數E,對于地球化學背景區域,它們的空間分布通常占全圖的絕大部分,其統計分布規律通常符合正態分布或對數正態分布;而奇異性區域(α≠E)所構成子集的分形維數有很多個,可以由f(α) 利用奇異性指數識別化探異常的效果經常被用來與襯值異常進行比較。陳志軍等(2009)探討了α值和滑動襯值(簡記為CV)之間的定量關系。當無標度區間上符合嚴格的冪律關系時,α的估值可任選2個尺度進行計算,有如下關系成立: (5) 式(5)中,la和lb分別表示較小和較大2個不同尺度的窗口;Δα和log(CV)相比較而非直接比較CV,在統計上更能區分辨別二者的異常能力。由于對數函數是典型的單調函數,log(CV)和CV具有相同的排序值,可以通過比較Δα和CV的排序值(或用百分位數)來判別異常識別能力(陳志軍, 2007)。 局部奇異性指數的計算通常要考察多個尺度的趨勢性變化,由統計分形關系來確定,在log-log雙對數圖中采用回歸分析技術來估值,相對僅由2個窗口度量值所確定的滑動襯值來說,Δα值對局部異常強度的指示作用更穩健,更能代表局部范圍內異常的總體水平。滑動襯值則常因2個窗口選擇的隨意性而易受波動。通常,局部奇異性指數相比滑動襯值異常識別能力更佳(陳志軍等, 2009)。 2.1 柵格數據模型 從計算簡便性考慮,二維情形下基于柵格數據模型的計算方案效率最高。在柵格形式表達中,雖然對于柵格的形狀沒有限制(如等三角形、等六邊形等),然而正方形網格的簡單性、運算方便性、直觀性使得這種形式的柵格數據模型最為普遍。這些形狀一樣的正方形網格作為基本單元(單元格或稱像元)組成了形如數學中規則排列的矩陣。像元大小、空間位置及像元值構成了柵格數據的基本要素。像元大小表示數據的最小尺度,或稱空間分辨率;像元的取值即為空間對象的測量值;每個像元有唯一的行索引和列索引,測量值的空間位置隱含于柵格行列位置,也即可根據行列號轉換成相應的空間坐標。一個柵格數據集描述了某個專題內容在區域的位置、特性和空間上的相對位置。 眾多GIS軟件都支持柵格數據類型,并且有眾多數據格式。表1展示了ArcGIS和Surfer 2種主流的柵格數據文本文件格式,由此可以直觀地了解柵格數據的編碼規則。在對這兩類柵格數據文件進行相互轉化中,需要注意ArcGIS ASC文件所定義的左下角位置是左下角柵格單元的左下邊界的角點,而Surfer 6 Text Grid柵格數據所定義的X最小值和Y最小值位于柵格單元的中心位置,因此兩者偏差半個像元大小(表1示例文件中該偏差值為50)。ArcGIS ASC文件文件頭信息可自定義缺失數據標記值,如-99 999;而在Surfer 6 Text Grid文件中,缺失數據默認標記為1.701 41E+038。此外,兩者數據陣列的存放方案是不一樣的,具有上下對稱的關系。 表1 ArcGIS和Surfer柵格數據文件格式示例 2.2 局部奇異性分析算法中的量綱問題 局部奇異性分析算法通常基于柵格數據的多窗口鄰域統計來開展計算。利用柵格數據在鄰域分析方面的簡便性,可以快速獲得各個空間位置上不同尺度的滑動平均值,進而在log-log坐標下進一步計算奇異性指數(空間維數E=2)。柵格數據模型具有統一的幾何支撐,意味著像元分辨率范圍內研究對象具有同質性。對于某個柵格數據來說,空間分辨率一旦確定,局部奇異性特征尺度區間的最小值也就隨之確定。因此,獲取的局部奇異性指數是在一定尺度區間上估計出來的,揭示的是統計分形規律,在現實中特征尺度不能無限趨近于0。 局部奇異性分析方法算法的一些關鍵計算技術如:空間覆蓋系列盒子的各向同性、各向異性窗口的多種構造方式、空間加權處理、掩模矩陣構置、等效尺度的確定及log-log最小二乘線性擬合、數據邊緣區擴邊、多種測度參見文獻(陳志軍,2007)。為便于推導迭代算法,這里有必要分析一下尺度ε的處理問題。ε的量綱是否及如何影響計算結果?假定窗口由小到大依次遞增序列為:lmin=l1 2.2.1ε=l具有長度量綱 此時,c值在理論上的量綱是[ρ][l]Δα,估計Δα值(或α值)和c值的回歸方程可表示為: log〈ρ(x,li)〉 = log(c(x))-Δα(x)×log(li),i=1,2,3,…,m (6) 用α(x)表示,也即 log〈ρ(x,li)×li2〉=log(c(x))+α(x)×log(li),i=1,2,3,…,m (7) 其中,Δα(x)和log(c(x))為待定系數。式(6)與(7)相比,式(6)在形式上更為簡單,但是由于Δα(x)均值水平接近于0而使得對普通最小二乘(OLS)準則下回歸方程顯著性水平偏低,作者建議先用式(7)形式計算α(x),再由式(3)轉換成Δα(x)。此時,回歸直線段斜率即代表α(x),通常與柵格數據模型的維數2比較接近,然后由式(4)計算Δα(x)。當li=1(帶長度單位)時,可以獲得擬合值即為c(x)值。這里,需要注意到c(x,l1=1)、c(x,l1=lmin)、c(x,l1=lcellsize)三者可以是完全不同的,c(x,l1=lcellsize)才表示原始柵格分辨率意義下對原始測量值的估值。 2.2.2ε=l/L=N(l)/N(L) 消除量綱 引入正規化尺度參數L(為一定值),通過比值l/L消除ε的量綱。在柵格數據模型中,可以直接用窗口邊長所占像元個數的比值:N(l)/N(L)等效表達物理長度比值l/L,這里,N(·)操作符表示取長度覆蓋的柵格像元數,允許取小數表示等效個數。對非方形窗口,借鑒面積與邊長的關系,N(l)的大小可由窗口覆蓋像元數的平方根來等效表達。此時,Δα(x)值與c值均無量綱,Δα(x)值大小與不消除量綱情形獲得的結果相同,而c值則不同。式(3)可轉變為: 〈ρ(x,l)〉=c(x,l)(l/L)-Δα(x) (8) 對x位置處奇異性指數及其系數的估計可由log(l/L)-log(ρ(x,l)×(l/L)2)圖中回歸直線來確定,對應回歸方程可表示為: log〈ρ(x,li)×(li/L)2)〉=log(c(x))+α(x)×log(li/L),i=1,2,3,…,m (9) L參數加入到模型中,增加了模型處理獲得c值的靈活性,以下介紹的迭代方法與L參數有緊密聯系。L參數的取值可以是多樣化的,下面列舉4種典型的情形。 (1)L=lcellsize(柵格數據空間分辨率),此時,ε的大小就是柵格像元個數,也即ε=l/L=N(l)。對柵格數據計算窗口邊長通過數柵格像元個數在實際中操作簡單,僅需對計算窗口的行列號進行操作,不涉及具體空間距離計算,因此在奇異性指數計算中使用頻繁,此種情形c(x)值為原始數據的非線性擬合值。 (2)L=lmax(尺度窗口序列的最大值),這種取值方式在許多分形計算場合常被采用。log(c(x))值在式(9)中為log-log圖中截距(此時li=L),相當于在lmax×lmax窗口滑動平均對數值的擬合值。在log-log擬合中,當L取lmax時,log(c(x))值在橫軸的最大值位置獲得,從回歸分析誤差角度考慮,由于偏離擬合數據的重心而有較大的誤差。 (3)L取值為尺度窗口序列{li} (i=1,2,3,…,m)的幾何平均值: 或表示成等效窗口數: (9) 此種情形克服了式(2)中的不足,log-log回歸分析中平移縱軸使之經過數據重心,從而使得c(x)估值的誤差最小化。用式(9)確定的L進行奇異性分析時,用c(x)值擬合相應窗口大小的滑動平均值具有最佳的預測可信度。 (4)L取值小于柵格數據的分辨率lcellsize。例如L=lcellsize/ 3,此時c(x)估計值表示了x位置處(lcellsize/ 3)空間分辨率意義下的分形插值結果。 綜上可見,ε的量綱對于Δα值(或α值)的估算沒有影響,而c值的大小及其量綱有差異,它的大小取決于正規化尺度參數L的取值方式。某些作者在開展局部奇異性分析模型時,對尺度指標ε的取值張冠李戴,不加區分:在實際處理中采用了像元個數N(l)來進行計算,卻聲稱窗口計算參數為空間距離某某千米變化到某某千米。盡管對于α(x)的估值不受影響,但嚴格來說這是不妥當的,忽視了c(x)值的數量水平、量綱及其應有的意義。 從模型計算的通用性角度考慮,筆者建議用形式上更為一般化的式(8)作為基于柵格數據模型的常規局部奇異性的算法。可以在連續區間[lmin,lmax]上內插預測及適度外推預測任意窗口大小的滑動平均結果,或者獲得更小分辨率的分形插值結果。本研究所介紹的迭代方法是在L>lcellsize的情形下作出推導的,此時c(x)值與原始數據具有相同的量綱,且c(x)值代表了L尺度上的光滑成分。 3.1 迭代方法的基本思想 局部奇異性分析方法的特點在于采用局部化的α估值與空間拓撲維數E值的差異性來實現異常識別,于是合理估計α值(或Δα值)就成為一個關鍵問題。利用一系列方形窗口基于柵格模型的局部奇異性分析算法簡單,運算快捷。然而,嵌套的這一系列尺度窗口一次性計算所得的α值是最好的嗎?最優的α值應該符合怎樣的數學條件?筆者注意到與α值所伴隨的c值的特性有其重要作用。從式(4)可見,局部奇異性分析可將原始數據分離出兩大因子Δα成分和c成分。如果各個位置處的Δα值完全刻畫了奇異性的強度,那么由全體c值構成的c集就應成為一個非奇異性的成分;否則,若c集仍帶有奇異性,那么對應的Δα集便與理想的奇異性指數不對應,c集還可以繼續分離出新的Δα成分和c成分。Δα成分和c成分應該分別代表奇異性因子和非奇異性因子,c成分應足夠光滑,沒有奇異性,具有良好的連續性和可微性。在實際計算中,獲取Δα成分的log-log擬合過程中總會存在剩余誤差,它并沒有完全保證c成分不再帶有奇異性信息。設法去除c集中的奇異性成分,使之具有足夠高的光滑性,而將奇異性信息都歸屬于Δα集,這成為筆者研究局部奇異性分析迭代方法來優化α估值的關鍵思路(Chen et al, 2005, 2007)。 3.2 迭代方法的數學表達 記α*(x)和c*(x)分別為期望獲取的一種最優的局部奇異性指數和局部系數,仍有 ρ(x)=c*(x)εα*(x)-E=c*(x)ε-Δa*(x) (10) 成立。這里,ε=l/L且L>lcellsize,盒子B(x,ε) 內的平均密度簡記為ρ(x),ρ(x)在所有空間位置的取值構成的數據集合稱為ρ集,c*(x)在所有空間位置的取值構成的數據集合稱為c*集。注意到,c*集與ρ集量綱相同,c*集反映了比ρ集更大尺度上的滑動平均非線性擬合信息,c*集比ρ集具有更小的離散程度。c*集可看作是ρ集的一個粗尺度逼近,其細節(粗糙度)信息保存在Δα*圖中,理論上的c*集應不再具有多重分形特征,這樣ρ集的奇異性信息都應集中反映在α*集中。若對c*集再做奇異性分析,則其計算所得的各個α值都趨近于同一個常數,即空間拓撲維數E。 基于同尺度的局部系數圖迭代方法可以不斷校正奇異性指數,將具有奇異性的c(x)通過迭代不斷演化成非奇異的(Chen et al, 2007):首先將ρ(x)分解成c0(x)和α0(x),被估計出來的c0(x)可以進一步估計其局部奇異性,即把它當作新的ρ(x),再次進行分解得到新的c1(x),(下標1表示進行第1次迭代數,下同),可知c1(x)的離散程度比c0(x)小,比ρ(x)更小,不斷重復這樣的過程,可以預料,最終獲取的局部系數圖將趨近于一種平穩狀態,最終將不再具有奇異性,此時它的局部奇異性指數α趨近于自身的歐氏空間維數E,即Δα趨近于0。迭代方法與常規的非迭代方法的區別在于前者考慮了局部系數c(x)的作用。 令c-1(x) =ρ(x),于是有如下迭代形式: ck-1(x)=ck(x)ε-Δαk(x),k=0,1,2,... (11) c集不斷視為新的輸入數據集,再次進行同樣的局部奇異性計算,如此循環,新產生的c集將變得越來越光滑,趨近于一種平穩狀態……于是最終可獲得所期望的c*集。迭代分解的示意見圖1。 圖1 局部奇異性分析迭代方法示意圖 假定進行了n次迭代時達到理論上的迭代終止條件:αn→0時,研究獲取包括第0次(非迭代)和n次迭代的結果,有式(12)成立。 對比式(10)和式(12),于是可得最終局部奇異性指數及系數的估值,見式(13)。 (13) 從中可見,當n=0時,迭代方法退化為常規方法;n>1時,迭代方法獲取的最終奇異性指數α*的結果中則多了一個附加校正項,Δα*的表達則更為簡練,是歷次迭代所產生的Δαk的累加。可見,迭代方法具有對常規方法結果進行校正的能力,且其形式簡潔。奇異性迭代方法得到了學者的關注,α*被稱為最終奇異性指數(Agterberg, 2012)。 3.3 迭代終止條件與邊緣效應 理論上的迭代終止條件要求Δαn中處處取值為0,在實際計算中這一條件過于嚴格,可用均方根誤差(RMSE)作為判別條件,而均方根誤差在數值上與Δαn的標準方差等價,于是,可直接用s(Δαk) < eps(eps為精度要求,例如0.01)迭代約束條件。 當精度要求過高時,將導致迭代過程無法在期望時間內結束,因此與一般的迭代算法一樣,可人為限制迭代最多次數N0,使之定能在有限時間內完成計算。當迭代計數器k>N0時,跳出循環,終止迭代。作者對地質勘查數據的大量計算表明,經過數次迭代(通常3~5次)就能大幅度地降低c集的不光滑度,獲得較理想的奇異性指數。當N0取值為0時,迭代方法就退化為常規方法。 當多尺度窗口滑動到柵格數據邊緣位置時,一些窗口部分位置因覆蓋于數據范圍之外而造成數據獲取的不完整,從而產生邊緣效應,窗口尺度越大且迭代次數越多,邊緣效應會越來越嚴重。對此問題,可以采用傅里葉變換類似的手段來擴邊,補齊數據范圍之外的像元取值;還可以采用缺失數據處理手段,僅對有效數據作鄰域統計量計算,獲得等效的平均密度。 3.4 基于柵格數據的迭代算法設計 局部奇異性分析的迭代算法可設計如下: 設置多尺度窗口參數{li},i=1,2,3,…,m 設置L參數且L>lcellsize 設置迭代精度eps與最多次數N0 輸入數據初始化為原始柵格數據 最終的局部奇異性指數Δα*所有元素初始化為0 for(intk= 0,i<=N0;k++) { //約束迭代次數不超過N0 for(inti= 0,i for(int j=0;j 計算[i][j]柵格焦元位置m個不同 大小窗口的鄰域平均值 //** 雙對數log-log回歸分析獲得奇異性 指數αk[i][j]和系數ck[i][j] } } Δαk=E-αk; //默認二維情形E=2;退化為方向性奇異性,則E=1 Δα*+=Δαk; //最終局部奇異性指數的累計計算 if(s(Δαk)< eps) break; //迭代達到精度要求,結束迭代 else輸入數據賦值更新為計算所得的ck集 } c*=ck; //獲得最終的局部系數 注:**步驟可以采用積分圖快速算法。 利用C++編程語言在Windows平臺下開發了RasterDataMining 1.0軟件,實現了基于柵格數據模型的局部奇異性分析專業分析功能。以主流文本柵格格式ArcGIS ASC Grid、Surfer 6 Text Grid來讀寫文件,制圖功能則可在ArcGIS或Surfer平臺下完成。該軟件從柵格數據局部奇異性分析的深度應用需求出發,具有如下功能(圖2)。 圖2 局部奇異性程序功能界面(圖上帶圈數字編號說明內容見正文功能介紹) 具體功能按數字編號依次介紹如下。 (1) 實現局部奇異性常規方法和迭代方法,并支持缺失數據計算。 (2) 支持各向同性及各向異性鄰域形狀并自動構建多尺度窗口。 在柵格模型下直接以像元空間分辨率為單位來表達尺度大小,尺度大小為窗口邊長所占的像元數,正規化尺度參數L也采用此方案。鄰域形狀可選方形、圓形、矩形、橢圓,有寬度和高度2個維度。窗口數、最內窗口、半徑增量、旋轉角度幾項關鍵參數來創建多尺度鄰域形狀,其中,最內窗口設置值約定取奇數,默認為1,也可以設置成3、5等其他奇數值,此時的最小尺度大于像元的空間分辨率。多尺度窗口序列有2種自動構建方式:線性等間距(Linear space),形成等差數列;對數等間距(Log space),形成等比數列。在自動生成的基礎上,用戶可以自由修改尺度序列。 程序支持各向同性情形的奇異性分析,通過設置非等寬高的窗口參數(還可包括旋轉角度)來實現。開發了某個像元是否在1個橢圓內(帶旋轉角度)的快速判斷算法。 程序支持方向性奇異性分析計算。程序由二維自動退化為一維情形,即E=1。選擇矩形窗口(可設置旋轉角度),固定其中一個維度的窗口大小不變化。例如,在高度方向窗口數設置為1或者3等定值(長度單位為柵格空間分辨率)且尺度半徑增量固定為0,于是奇異性指數沿著東西方向進行計算。若高度窗口數固定為1,相當于原始柵格數據被分成多條東西向的一維數據序列;若高度窗口固定為3,則等效于原始柵格數據作南北向3個窗口的滑動平均后的多條一維數據序列。此時的奇異性指數圖可突出南北向的差異性。 (3) 支持自定義計算位置,包括2個方面。圖2中3a:自定義感興趣區域進行計算,有3種選擇:數據格網所有位置、數據格網有效數據為準、用戶文件自定義位置;圖2中3b:指定某一空間位置進行奇異性探查與預測(圖3)。 圖3 局部奇異性分析特定計算位置奇異性探查與預測 (4) 支持批量計算,包括2個方面。圖2中4a:對多套不同的多尺度窗口進行批量計算;圖2中4b:對多個輸入柵格數據進行批量計算。 (5) 輸出結果多樣化,滿足進一步分析的需要。結果文件保存不局限于奇異性指數,還包括系數c集,擬合優度等多種指標,可以追蹤歷次迭代的詳細結果,也可以只保留最終結果。 此外,程序還提供了友好的柵格數據管理功能(支持ArcGIS和Surfer柵格數據批量相互轉換)以及地圖代數常見分析功能。 為幫助用戶優化參數設置,程序提供了單個位置的計算功能,用戶可以獲得該位置的感興趣信息:數據子集提取、鄰域窗口統計、雙對數回歸分析、奇異性模型計算結果、因變量預測。圖3顯示WX數據集在行列坐標(53,75)位置處的奇異性計算信息,該位置計算所得Δα值為0.67(對應α值為1.33),表明具有較強的正奇異性,擬合優度系數達到95.6%,可以通過顯著性檢驗。按照所建立的奇異性模型,當窗口大小為lcellsize/2和lcellsize/3時,預測結果分別為22.67,29.70,明顯高于原始柵格像元值20.41,與該位置的正奇異性特征一致,這提供了一種非線性插值方法。對應窗口大小為3.5個像元單位時,也可以通過奇異性公式獲得預測值,為6.20,該預測值為分數維窗口內的滑動平均估值。 在前述參數設置條件下,增加迭代計算約束條件:標準誤差s(Δαk)≤0.01,最多迭代次為25次,對整個數據集計算全圖范圍的局部奇異性(圖4)。程序運行結果表明,當迭代到第20次時,s(Δαk)=0.009 7,于是終止迭代。圖4展示了20次迭代過程中計算結果空間模式和常見統計量的變化趨勢。圖4曲線展示了s(Δαk)隨迭代次數k的變化,可見由s(Δα0)到s(Δα1)具有最大的變化性,迭代4~5次后,s(Δαk)的下降速度越來越緩慢,趨近于0。與之相對應,局部系數c圖也變得越來越光滑。原始數據是一個典型的多重分形數據集,具有強烈的不均勻性,對原始數據制圖,僅能分辨有限的若干高值(顯性異常,形如“大型山峰”),而更多局部鄰域上相對高值(弱緩異常,形如“小型山峰”)難以識別,將數據轉換成對數后在一定程度上達到了異常增強效果,可以識別較多的局部異常。通過局部奇異性常規分析所獲得的Δα0圖可見,原始數據還有更多空間位置具有局部弱緩異常存在。通過迭代方法,可以獲得任意迭代次數后的最終奇異性指數,由圖4下面所展示的3個結果來看,異常的總體面貌雷同,但清晰程度各有差別。實際上,欲獲得較好的奇異性指數,結合s(Δαk)曲線的變化性,對該數據集迭代4~5次就可得到較優的結果。 此外,對于批量處理等功能,限于篇幅,在此不一一展示。綜上所述,所研發的基于柵格數據的局部奇異性分析程序計算效率高,功能全面,實用性強。核心算法代碼還編譯生成了動態鏈接庫,提供給第三方使用。軟件GeoDAS就采用了本程序的動態鏈接庫,將局部奇異性計算與可視化結合到1個環境中,促進了方法的推廣并方便了用戶的使用。 圖4 局部奇異性迭代分析結果空間模式和常見統計量趨勢(枚舉了迭代次數為0, 1,10,20的c圖和Δα圖,圖件由Surfer軟件生成,圖件渲染顏色僅表示該圖自身取值的相對高低,不同圖件相同顏色值所對應的數據值無對比性,常見統計量見左統計表) 在深入在剖析局部奇異性分析基本思想及計算方法的基礎上,引入正規化尺度參數L,提出了迭代方法來改進局部奇異性指數的估值。迭代方法使得在計算中通常被忽視的局部系數c值的作用被挖掘并利用。迭代分析方法的成立是建立在正規化尺度參數L大于柵格空間分辨率的基礎上,通過迭代,可以獲得越來越光滑的c圖,與此相伴,在Δα中將積累更多的奇異性信息,因此迭代分析方法對Δα估值有其良好的特性。不同的L參數取值,可以獲得不同的c值,增加了奇異性模型的靈活性。基于建立的奇異性模型,可以開展非線性空間插值、滑動平均估值。所設計的軟件功能強勁,為用戶應用迭代分析新方法提供了高效便捷的計算工具。不僅支持各向同性情形,還適用于各向異性尺度的奇異性計算和方向性奇異性計算。軟件的動態鏈接庫版本也在GeoDAS軟件中被推廣應用,促進了方法的推廣。 本研究提出的迭代方法的數學公式同樣適用于矢量數據模型。矢量數據作為最主要的空間數據類型之一,由于矢量數據空間位置的不規則性,相比柵格數據模型,需要優化算法提高時間效率,這將是后續研究的方向之一。目前研究的迭代策略是全圖幅同步進行的,迭代使用的鄰域形狀也是全區一樣,這些方面也可能進行局部化而優化迭代分析的結果。迭代方法中局部系數c集在迭代過程中間接地獲取更大范圍上的數據信息,具有加權滑動平均的效應。隨著迭代次數的增加,各空間位置的ck(x)值被磨光的速率可能是不一致的,全圖幅同步迭代將導致一些位置被過度計算。迭代次數越多邊緣效應越嚴重,這在解釋數據時需要引起注意。迭代過程中使用固定的鄰域形狀、固定的尺度變化范圍,簡化了計算,但忽視了局部系數在迭代過程中自身所發生的變化。本程序提供的批處理功能方便了用戶從多種計算方案中優選結果,但這還不夠智能化,更好的方案是從空間數據自身特點著手來發現最合適的窗口形狀及尺度變化范圍,例如借助空間U統計量方法(Cheng et al, 1996, 2007)。這些問題、難題的解決將有助于基于多重分形的局部奇異性方法的進一步發展與完善。 在寫作過程中,筆者與Agterberg博士進行了有益的探討,在此表示由衷的感謝! 成秋明.2000.多重分形理論和地球化學因素分布規律[J].地球科學:中國地質大學學報,25(3):311-318. 成秋明.2004.空間模式的廣義自相似性分析和礦產資源評價[J].地球科學:中國地質大學學報,29(6):733-744. 陳颙,陳凌.2005.分形幾何學[M].2版.北京:地震出版社. 成秋明.2006.非線性成礦預測理論:多重分形奇異性-廣義自相似性-分形譜系模型與方法[J].地球科學:中國地質大學學報,31(3):337-348. 成秋明.2007.成礦過程奇異性與礦產預測定量化的新理論與新方法[J].地學前緣,14(5):42-53. 陳志軍.2007.多重分形局部奇異性分析方法及其在礦產資源信息提取中的應用[D].武漢:中國地質大學(武漢). 陳志軍,成秋明,陳建國.2009.利用樣本排序方法比較化探異常識別模型的效果[J].地球科學:中國地質大學學報,34(2):353-364. 成秋明.2012.覆蓋區礦產綜合預測思路與方法[J].地球科學:中國地質大學學報,37(6):1109-1125. AGTERBERG F P. 2001. Multifractal simulation of geochemical map patterns[J]. Journal of China University of Geosciences, 12(1): 31-39. AGTERBERG F P. 2003. Past and future of mathematical Geology[J]. Journal of China University of Geosciences, 14(3): 191-198. AGTERBERG F P. 2012. Sampling and analysis of chemical element concentration distribution in rock units and orebodies[J]. Nonlin Processes Geophys, 19: 23-44. CHENG QIUMING, AGGTERBERG F P, BONHAM-CARTER G F. 1996.Spatial analysis method for geochemical anomaly separation[J]. Journal of Geochemical Exploration, 56(3): 183-195. CHENG QIUMING. 1999. Multifractality and spatial statistics[J]. Computers & Geosciences, 25(9): 949-961. CHEN ZHIJUN, CHENG QIUMING, CHEN JIANGUO. 2005. Significance of fractal measure in local singularity analysis of multifractal model[C]//CENG QIUMING, GRAEME BONHAM-CATER. Proceedings ofIAMG'05: GIS and Spatial Analysis. International Association for Mathematical Geology. Wuhan, China: China University of Geosciences Printing House, (1): 475-480. CHENG QIUMING. 2006. GIS-based fractal/multifractal anomaly analysis for modeling and prediction of mineralization and mineral deposits[C]//HARRIS J R. GIS Application in the Earth Sciences. St John’s, NL, Canada:Geological Association of Canada, Special book: 289-300.CHEN ZHIJUN, CHENG QIUMING. 2007. Generalized local singularity analysis and its application[J]. Journal of China University of Geosciences, 18(Special issue): 348-350. CHEN ZHIJUN, CHENG QIUMING, XIE SHUYUAN, et al. 2007. A novel iterative approach for mapping local singularities from geochemical data[J]. Nonlin Processes Geophys, 14: 317-324. CHENG QIUMING, AGTERBERG F P. 2009. Singularity analysis of ore-mineral and toxic trace elements in stream sediments[J]. Computers & Geosciences, 35(2): 234-244.EVERTZ C J G, MANDEBROT B B. 1992. Multifractal measures: Appendix B[M]//PEITGEN H O, JURGENS H, SAUPE D. Chaos and Fractals. New York: Springer Verlag, 922-953. Iterative approach to local singularity analysis and software implementation based on raster data CHENZhi-jun1,2,CHENGQiu-ming1,2,3,CHENJian-guo1,2 (1. State Key Laboratory of Geological Processes and Mineral Resources, China University of Geosciences, Wuhan 430074, China; 2. Faculty of Earth Resources, China University of Geosciences (Wuhan), Wuhan 430074, China; 3. Department of Earth and Space Science, Department of Geography, York University, Toronto M3J1P3, Canada) Weak anomaly identification was a challenging problem in the metallogeny prognosis and mineral resource assessment in recent years. Great attentions were drawn to the local singularity analysis based on multifractal theory for its new research ideas, simple method and beneficial effects to anomaly recognition. The authors introduced the singularity principles and its computational methods. The authors took into account the regularization scale parameter L and brought forward the iterative approach for the singularity analysis to improve the estimation of the singularity index. The iterative algorithm and software were realized and implemented using C++ language. This iterative approach could work not only for the isotropic case, but also could apply to the anisotropic scaling case and directional singularity index estimation. The dynamic-link library version of this software had been applied in GeoDAS which was professional GIS software for quantitative prediction of mineral resources. Local singularity analysis; Raster data; Multifractals; Iterative approach; Regularization scale parameter 10.3969/j.issn.1674-3636.2014.04.613 2014-08-18;編輯:陸李萍 國家自然科學基金項目(41272361, 40802081),中國地質調查局工作項目(12120113089300),中央高校基本科研業務費專項資金資助項目(CUG120102) 陳志軍(1978— ),男,副教授,博士,主要從事數學地質的教學與科研工作, E-mail: chenzhijunCS@163.com P628 :A :1674-3636(2014)04-0613-10
2 基于柵格數據的算法剖析
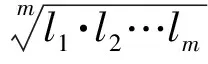
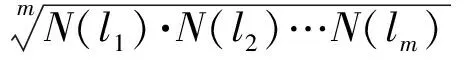
3 迭代方法及算法設計

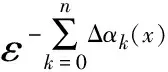
4 軟件功能實現及其效果


5 結 論
6 致 謝

