基于粒子群算法的地震預報方法研究①

張曉煜，李 向

（鄭州航空工業管理學院計算機科學與應用系，河南 鄭州 450015）

0 引言

傳統地震預報研究建立在人們對震例數據和前兆觀測數據的分析之上，而隨著地震臺網前兆觀測數據的飛速猛增和地震預報研究的深入，該方法已不能滿足現實需要［1］。數據挖掘的任務通常可以概括為兩類：對海量數據的描述性挖掘和預測性挖掘。隨著數據挖掘技術的不斷發展，各類數據挖掘算法在財務分析、通信運營、生物科技、入侵檢測等應用領域得到廣泛應用，該技術在地震預報中也有廣泛的應用前景［2］。代表性的研究有：文獻［3］提出了用神經網絡方法通過大量樣本的學習抽取隱含在數據中的震級識別因果關系，但是該模型依賴于樣本選擇，可重用性較差，且計算收斂性問題有待研究。文獻［4］提出了一種新的模糊規則提取方法，采用基于山峰函數的減法聚類自適應確定聚類中心，并給出4條基于孕震空區長軸的震級預報模糊規則。由于該方法基于自組織神經網絡模型訓練規則，同樣是基于有效樣本的震級預報模型，并且預報規則僅考慮了前兆觀測眾多數據種類的一種。文獻［5］把時間序列相似性匹配的概念和方法引入到地震預報中，該方法的重點是建立時間序列的相似性度量模型，是對地震歷史源數據和地質構造專家經驗知識的相似性挖掘。文獻［6－8］對地震參數預測預報中粒子群算法的應用進行了深入研究，建立了不同的反演模型，分別用于反演震源時間函數、振幅譜、斷裂活動速率等參數。文獻［9］利用粒子群算法優化LSSVM模型的懲罰因子和核函數參數，建立了PSO地震預測模型，其本質是利用非線性系統建模進行預測，該模型使用有限樣本數據檢測模型預測結果及誤差，可得到在已有數據信息下的最優解。

由于影響地震的因素較多，實際地震預報具有震級、時間、區域等預報多重困難的特性。一方面震級與前兆及異常的種類有一定關系，另一方面地質構造與異常及時間又有極大的不確定性。因此傳統的數據挖掘及人工智能算法往往不能正確預報。

本文提出基于粒子群聚類算法的地震預報方法，面向前兆數據的多維特性，利用群體智能的分布式和自組織特征，建立新的地震預報模型。該方法克服了神經網絡方法對數據樣本選取的依賴，不需要設計網絡拓撲結構，對史源震例數據的分析和實驗結果表明，該方法優于經典的k－means聚類算法，穩定性強，對震級的預報準確性更高。

1 粒子群算法的基本原理

群體智能研究主要包括蟻群算法和粒子群算法［10］。其中粒子群算法［11］是由 Kennedy和 Eberhart通過對鳥群、魚群和人類社會某些行為進行觀察研究，于1995年提出的一種新穎的進化算法。粒子群優化（Particle Swarm Optimization，即PSO）是一種新興的基于群體智能的啟發式全局隨機搜索算法，具有易理解、易實現、全局搜索能力強等特點，有很多學者對此進行研究，并建立模型推廣應用于數據分析［12］。

與其他進化算法一樣，粒子群算法也是基于“種群”和“進化”的概念，通過個體間的協作與競爭，實現復雜空間最優解的搜索；同時，PSO又不像其他進化算法那樣要對個體進行交叉、變異、選擇等進化算子操作，因此具有很好的生物社會背景，容易理解、參數少且易實現，對非線性、多峰問題具有較強的全局搜索能力。

粒子群算法有6個基本步驟，可用流程圖1表示，具體描述如下：

圖1 粒子群算法流程圖Fig.1 The flow chart of particle swarm algorithm

（1）初始化粒子群，包括群體規模N ，每個粒子的位置xi和速度Vi；

（2）計算每個粒子的適應度值Fit［i］；

（3）對每個粒子，用它的適應度值 Fit［i］和個體極值Pbest（i）比較，如果 Fit［i］＞Pbest（i），則用Fit［i］替換掉Pbest（i）；

（4）對每個粒子，用它的適應度值Fit［i］和全局極值gbest比較，如果 Fit［i］＞Pbest（i）則用Fit［i］替換gbest；

（5）根據公式（1）和（2）更新粒子的速度υi和位置xi；

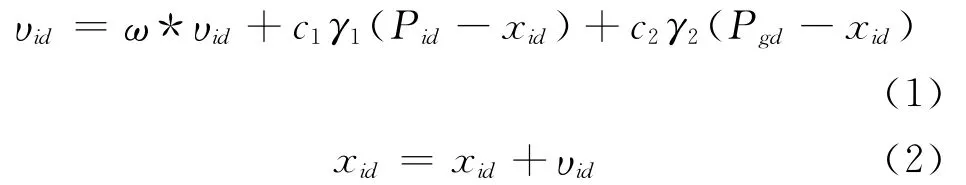
（6）如果滿足結束條件（誤差足夠好或到達最大循環次數）退出，否則返回（2）。

在公式（1）和（2）中：c1和c2為學習因子，也稱加速常數，γ1和γ2為［0，1］范圍內的均勻隨機數。式（1）右邊由三部分組成，第一部分為“慣性”部分，反映了粒子的運動習慣，代表粒子有維持自己先前速度的趨勢；第二部分為“認知”部分，反映了粒子對自身歷史經驗的記憶，代表粒子有向自身歷史最佳位置逼近的趨勢；第三部分為“社會”部分，反映了粒子間協同合作與知識共享的群體歷史經驗，代表粒子有向群體或鄰域歷史最佳位置逼近的趨勢。根據經驗，通常c1＝c2＝2。i＝1，2，Λ，D。υid是粒子的速度，υid∈［－υmax，υmax］，υmax是常數，由用戶設定用來限制粒子的速度。

2 基于粒子群聚類的地震預報

2.1 數據背景

地震學異常指標可以分成測震學指標和前兆指標兩大類。在《中國震例》一書中，按照觀測手段統計，前者測震學異常指標有74項，后者前兆異常指標有84項。對于這些指標的含義，在地震學分析預報方法程式指南［13］中有明確說明。有學者專門研究如何從眾多復雜的地震異常指標中篩選出核心異常的約簡算法，文獻［3］選擇在歷史震例數據中出現次數相對較多的14項異常指標作為基礎數據進行分析。這14項異常指標可分為兩類：

（1）地震學異常時間：條帶、空區、應變釋放、地震頻次、b值、地震窗、波速比。

（2）前兆異常時間：短水準、地傾斜、地電、水氡、水位、應力、宏觀。

式中：yi,j表示新位置的植株，xi,j∈[aj，bj]表示Xi的第j條路徑值，aj，bj分別為搜索空間的上邊界值與下邊界值，α是[0,1]的隨機數。將種群按照適應度值優劣分為兩類：

由于一次地震前可能出現多臺異常（即多個臺站觀察都觀察到該類異常），并且一項異常可能在孕震的不同階段出現，因此當某項前兆異常在多個臺站出現，可根據常規方法，取各臺站加權和為研究對象，計算公式如式（3）所示：

式中tij為某臺站某項前兆異常的持續時間；ωj為權值，計算公式為

需要說明的是，如果某臺站的某項異常在中期、短期或臨震3個階段中都有異常，《中國震例》一書中取3個異常持續時間，而我們是取異常開始至發震的時間段為tij；如在2個階段中有異常，則取其2個異常時段的時間之和為tij。

本文選擇典型的地震震例驗證基于粒子群聚類的地震預報方法，實驗中把震級分為三組，第一組為3次7級以上地震序列；第二組為9次6級至6.9級地震序列；第三組為18次5級至5.9級地震序列，實驗數據如表1所示。

表1 地震樣本數據［3］Table 1 The sample data of earthquake［3］

2.2 算法步驟

本文所提出的基于粒子群聚類的地震預報算法模型描述如下：

（1）對震例原始數據進行歸一化，消除量綱效應。

采用區間值歸一化變換法對各維數據進行無量綱化處理，設數據樣本集為，其中 xi，j表示第i個樣本的第j維值，n表示樣本的個數，p表示樣本的維數。經歸一化處理之后的樣本可以表示為，計算公式如式（5）所示：

（2）初始化算法參數。

設定粒子數n，對于每個粒子，其位置xi和速度Vi，確定 的r1和r2的初始值為0，在［0，1］范圍內由程序自動選取均勻隨機數，用于計算更新每個粒子的位置和速度。

（3）應用粒子群算法加快速度，設計更新策略。

（4）設計評價函數，如果算法滿足評價函數，則停止算法，輸出最優解，否則轉到步驟（3）。

3 實驗結果與分析

為了驗證基于粒子群聚類算法在地震預報中的正確性及效率，在Matlab 2007a環境下進行實驗并與經典的k－means聚類算法對比。

3.1 實驗結果及準確率分析

經過多次實驗，算法中粒子群數目設置為500，參數設置為：α＝0.5，k＋＝0.8，k－＝0.5。圖2給出了聚類結果譜系圖。

從圖2中可看出，粒子群聚類算法用于地震預報效果較好，具體數據結果如表2所示。表中分類結果的1代表5～6級地震，2代表6～7級地震，3代表7級以上地震。利用k－means聚類的實驗共進行了20次，表2中給出的是最好的一次結果，其中加粗顯示的為震級分類錯誤的序列。

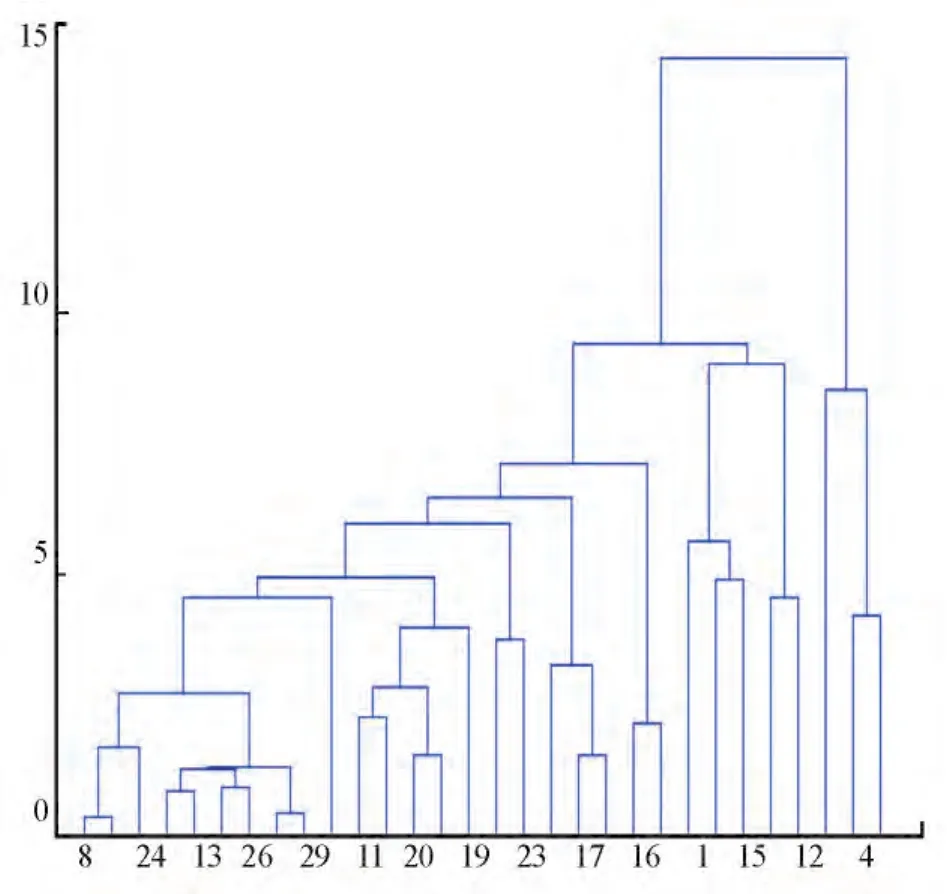
圖2 聚類分析譜系圖Fig.2 The pedigree chart of cluster analysis

從表2中數據分析可知，k－means算法的總體預報準確率僅為73.3%，而粒子群聚類算法可將準確率提高到83.3%。與k－means算法的結果對比發現，粒子群算法可以將6級以下及7級以上的震級完全正確區分開，而三類震級中，k－means算法準確率分別為88.7%、44.3%和66.7%。

表2 粒子群算法與k－means算法分析地震數據的結果Table 2 The analysis results of PSO and k－means algorithm

3.2 穩定性與時間復雜性分析

對算法步驟和代碼分析可知，基于粒子群聚類的地震預報算法時間復雜度為O（n），空間復雜度為O（n2）。

為了分析算法穩定性和時間復雜性，隨機選擇5次實驗結果計算類間平均距離和所用時間，如表3所示。可看出在地震震級預報中，雖然粒子群算法比k－means算法稍微耗時一點，但是粒子群聚類算法進行聚類的平均距離比k－means算法要小，這表明粒子群聚類算法比經典的k－means聚類算法有較好的穩定性優勢。

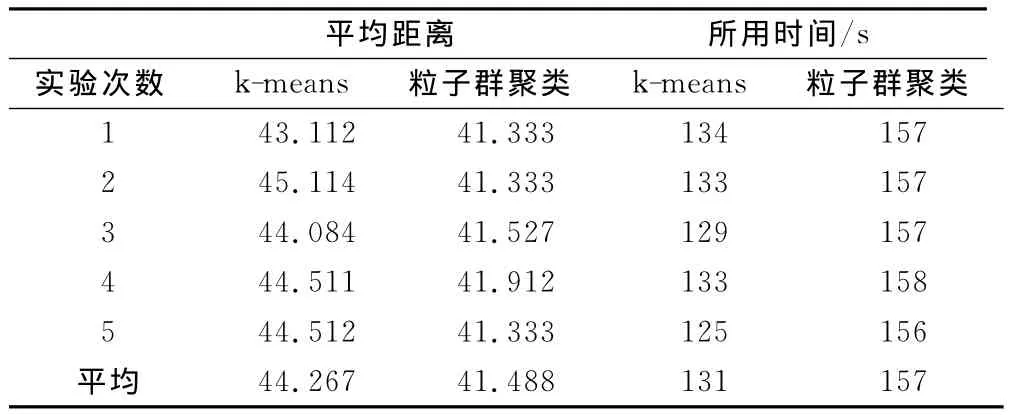
表3 粒子群算法與k－means算法處理地震數據的對比Table 3 The comparison of earthquake data processing of PSO algorithm and k－means algorithm

4 小結

本文采用數據挖掘技術結合群體智能粒子群算法來研究地震預報。實驗結果表明，粒子群聚類算法與經典聚類算法k－means相比雖然在計算速度上稍遜一籌，但聚類的平均距離較小，且不依賴于數據樣本特征，具有全局優化能力，可以更有效地找到最優解。而且粒子群算法可用于多維數據分析，面向不同數據樣本時，能根據不同的衡量參數自行優化，在應用中很有競爭力，是值得深入研究的方法。對于將數據聚類后，如何進行類內更細的分級需要深入研究。當然，這里也需指出，計算機和聚類算法只能是作為地震預報的輔助，并不能取代人們對地震學規律的認識、分析和表達。

（References）

［1］王煒，林命週，馬欽忠.數據挖掘及其在地震預報中的應用前景［J］.國際地震動態，2005，12：1－13.WANG Wei，LIN Ming－zhou，MA Qing－zhong.The Application Prospect of Data Mining in Earthquake Prediction［J］.Recent Developments in World Seismology，2005，12：1－13.（in Chinese）

［2］HAN J.W.Kamber Micheline，PEI J.Data Mining Concept and Techniques（2nd）［M］.San Francisco，Morgan Kaufmann Publishers，2006：359－362.

［3］王煒，蔣春曦，張軍，等.BP神經網絡在地震綜合預報中的應用［J］.地震，1999，19（2）：118－126.WANG Wei，JIANG Chun－xi，ZHANG Jun，et al.The Application of BP Neural Network to Comprehensive Earthquake Prediction［J］.Earthquake，1999，19（2）：118－126.（in Chinese）

［4］吳淑芳，吳耿鋒，王煒.一種新的模糊規則提取方法［J］.計算機工程，2005，31（6）：157－159.WU Shu－fang，WU Geng－feng，WANG Wei.A New Method for Fuzzy Rule Extraction［J］.Computer Engineering，2005，31（6）：157－159.（in Chinese）

［5］吳紹春，吳耿鋒，王煒，等.尋找地震相關地區的時間序列相似性匹配算法［J］.軟件學報，2006，17（2）：185－192.WU Shao－chun，WU Geng－feng，WANG Wei，et al.A Timesequence Similarity Matching Algorithm for Seismological Relevant Zones［J］.Journal of Software，2006，17（2）：185－192.（in Chinese）

［6］柳旭峰，許才軍.利用改進的粒子群算法反演視震源時間函數［J］.地震學報，2013，35（3）：151－159.LIU Xu－feng，XU Cai－jun.Retrieving Apparent Source Time Function by Improved PSO Algorithm［J］.Acta SeismologicaSinica，2013，35（3）：151－159.（in Chinese）

［7］鄭建常，陳運泰.基于粒子群優化的雙力偶模型振幅譜反演方法及應用［J］.地震學報，2012，34（3）：308－322.ZHENG Jian－chang，CHEN Yun－tai.Amplitude Spectrum Inversion for Double－couple Source Method with Particle Swarm Optimization Algorithm［J］.Acta Seismologica Sinica，2012，34（3）：308－322.（in Chinese）

［8］張永志，徐海軍，王衛東，等.渭河盆地斷裂活動速率的粒子群算法反演［J］.西北地震學報，2011，33（4）：322－325.ZHANG Yong－zhi，XU Hai－jun，WANG Wei－dong，et al.Inversion on Slip Velocity of Main Faults in Weihe Basin by Particle Swarm Optimization Algorithm with GPS Data［J］.Northwestern Seismological Journal，2011，33（4）：322－325.（in Chinese）

［9］徐松金，龍文.基于粒子群優化最小二乘向量機的地震預測模型［J］.西北地震學報，2012，34（3）：220－233.XU Song－jin，LONG Wen.Earthquake Forecast Model Based on the Particle Swarm Optimization Algorithm Used in LSSVM［J］.Northwestern Seismological Journal，2012，34（3）：220－233.（in Chinese）

［10］余建平，周新民，陳明.群體智能典型算法研究綜述［J］.計算機工程與應用，2010，46（25）：1－4.YU Jian－ping，ZHOU Xin－min，CHEN Ming.Research on Representative Algorithms of Swarm Intelligence［J］.Computer Engineering and Application，2010，46（25）：1－4.（in Chinese）

［11］Kennedy J，Eberhart R.Particle swarm optimization［C］∥Proceedings of the 4th IEEE International Conference on Neural Networks.Piscataway：IEEE Service Center，1995：1942－1948.

［12］王萬良，唐宇.微粒群算法的研究現狀與展望［J］.浙江工業大學學報，2007，35（2）：136－141.WANG Wan－liang TANG Yu.The State of Art in Particle Swarm Optimization Algorithms［J］.Journal of Zhejing University of Technology，2007，35（2）：136－141.（in Chinese）

［13］國家地震局科技監測司.地震學分析預報方法程式指南［M］.北京：地震出版社，1990：7－15.Science and Technology Monitoring of China Earthquake Administration.The Method and Program Guide of Seismological Analysis and Prediction［M］.Beijing：Seismological Press，1990：7－15.（in Chinese）