基于EMD的生物雷達回波信號噪聲抑制研究

孫權，張洋，曹陽，溫中一

中國人民解放軍海軍總醫院 醫務部，北京 100048

基于EMD的生物雷達回波信號噪聲抑制研究

孫權，張洋，曹陽，溫中一

中國人民解放軍海軍總醫院 醫務部，北京 100048

目的基于經驗模態分解（EMD）的多尺度時域濾波特性，抑制生物雷達回波信號噪聲。方法將經過預處理的雷達回波信號進行EMD分解，獲取固有模態函數（IMF）分量；根據噪聲與信號自相關函數的特性差異將IMF區分為有用信號占主導模態與噪聲占主導模態兩部分；然后用基于小波軟閾值的去噪方法提取噪聲占主導模態部分中的有用成分，與有用信號占主導模態部分的固有模態函數疊加，獲取雷達回波信號中的生命信息。結果基于EMD的噪聲抑制方法有效地去除了雷達回波信號中的高頻噪聲成分，提取出了有用信息。結論基于EMD的噪聲抑制方法能為生命體目標的識別提供更多信息。

生物雷達；經驗模態分解；固有模態函數；噪聲抑制

生物雷達融合了雷達技術和生物醫學工程技術，可穿透非金屬介質（磚墻、廢墟等）探測生命體信息（呼吸、心跳、 體 動等）[1-2]。 生物雷達經歷了連續波（Continuous Wave，CW）生物雷達和超寬帶 (Ultra Wideband，UWB)生物雷達兩個發展階段，UWB生物雷達因具有高距離的分辨力和目標識別力等優點已成為研究熱點[3-4]。在實際應用中，生物雷達發射的電磁波穿透障礙物照射到人體目標，經反射產生雷達回波信號，但信號中往往含有大量的雜波和噪聲，人體生命信息非常微弱。因此，去除雜波和噪聲，提取回波信號中有用的人體信息是生物雷達研究的難點。

生物雷達回波信號去噪方法中，常用的是傅里葉變換去噪[5]。生物雷達回波信號中包含的人體呼吸、心跳信號均屬于低頻信號，通過低通濾波器能去除高頻噪聲，保留大部分有用的人體信號，這種方法在信號平穩且具有明顯區別于噪聲的頻譜特性時比較有效。但雷達回波信號屬于非平穩信號，且傅立葉變換方法不具有時頻分析的局 域 性[6]，去噪的同時也平滑了信號的突變部分，可能導致突變位置攜帶的重要信息丟失。小波變換作為一種非平穩信號分析與處理的工具，具有多分辨率的特點，可以方便地從混有強噪聲的信號中提取原始信號，在信號濾 波 去噪 方 面 得 到 了 廣 泛 應 用[7]。 小 波 基 選 擇 的 正 確 與否很大程度上影響小波去噪的效果，但小波基的選擇具有一定的主觀性和經驗性，自適應性相對缺乏，給實際應用帶來了不便[8]。

美國工程院院士 N.E.Huang 等人提出了一種可用于非線性和非平穩信號處理的新的時頻分析方法 Hilbert-Huang變換（簡稱 HHT）[9]。HHT 吸取了小波變換多分辨率的優勢，同時克服了小波變換中需要選擇小波基的困難，可以用于生物雷達回波信號的濾波和去噪[10]。雷達回波信號信噪比較高時，基于固有模態函數（Intrinsic Mode Function，IMF）分量能量分析與小波軟閾值去噪的方法能有效地去除回波信號的高頻成分，保留低頻有用人體信息[11]。然而在低信噪比情況下，基于 IMF 分量能量的分析方法無法確定噪聲占主導模態部分與有用信號占主導模態部分的分界點，無法針對不同 IMF 分量特點提取其中的有用人體信息。本文利用基于噪聲與信號自相關函數特性差異的方法來確定 IMF 分量中噪聲占主導模態部分與有用人體信息占主導模態部分的分界點，在低信噪比情況下達到既能去除噪聲，又能最大限度地保留信號中有用成分的目的，為生物雷達識別人體目標奠定良好的基礎。

1 UWB生物雷達系統

UWB生物雷達系統由脈沖振蕩器產生脈沖信號，觸發電磁脈沖發生器產生窄脈沖，并通過發射天線輻射出去。反射信號經過接收天線送到取樣積分器，由脈沖振蕩器產生的信號經過延時電路產生距離門，對接收信號進行選擇。信號通過積分電路，實現對成千上萬個脈沖的積累，提高信噪比，然后進行放大濾波，經高速采集后送入計算機。一般情況下，UWB 雷達中心頻率越低，穿透力越強[12],因此該系統采用了中心頻率較低（400/500 MHz）的 UWB 雷達，以滿足實際應用中對穿透力的要求。系統原理框圖，見圖1。

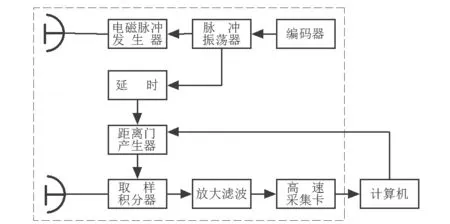
圖1 基于UWB雷達的非接觸生命探測系統原理框圖

2 噪聲抑制方法

2.1 EMD算法

經 驗 模 態 分 解（Empirical Mode Decomposition，EMD）是一種基于信號局部極值特征的自適應信號分析方法，可將復雜信號分解成有限數目、不同尺度的數據列之和，每個子數據列稱為 1 個 IMF 分量，都具有準正弦特性和窄帶特性。每個 IMF 分量需要滿足以下條件 ：① 在整個信號長度上，信號極值和零點的數目必須相等或最多相差1個；② 在任意一點，由極大值點定義的上包絡線和由極小值點定義的下包絡線的平均值為0。

2.2 EMD分解

EMD 分解過程也稱為篩分過程，即通過篩分得到 IMF分量，篩分過程如下：

（1）找出信號x(t) 中所有極值點，然后利用 3 次樣條函數分別擬合出極大值點與極小值點的上包絡線與下包絡線，求出上、下包絡線的均值m1(t)。

（2）將信號 x(t) 減去包絡線均值 m1(t) 得到 1 個新序列h1(t)，即 ：

h1(t) 通常并 不是 1 個平穩信 號序列，將其 作為待 處理信號x(t)，重復步驟①、②直至滿足判定條件 ：

（3）將信號 x(t) 減去 C1(t) 得到 1 個去除了高頻成分的信號序列r1(t) ：

（4） 對 r1(t) 重 復 上 述 3 個步 驟 得到 第 2 個 IMF 分量C2(t)，如此重復下去， 直 至 得 到 的 rn(t) 為一單 調 函 數 或常量，篩分過程結束，rn(t)通常表示原信號的趨勢項或直流分量，至此EMD分解過程結束。

經過 EMD 篩分，原信號x(t)被分解為有限個 IMF 分量：C1(t)，C2(t)，…，Cn(t) 和 1 個余項 rn(t)，因此原信號可表示為：

信 號 經 EMD 分 解 為 IMF 分 量 C1(t)，C2(t)， … ，Cn(t)，階數低的 IMF 分量對應信號的高頻部分，一般信號尖銳部分主要為噪聲 ；階數高的 IMF 分量對應信號的低頻部分，一般有用的人體信息集中于該部分，且該部分中噪聲影響很小。

2.3 基于EMD的噪聲抑制方法

Wu 和 Huang[13]等研究結果表明 ：EMD 分解的高斯白噪聲信號分量的能量隨著分解階數的增加而逐漸減小，因此認為 IMF 分量能量的第一個極小值點即為噪聲占主導模態部分與有用信號占主導模態部分的分界點，基于EMD的噪聲抑制方法的主要思想就在于尋找該分界點。以EMD分解得到的 IMF 階數為橫坐標，各階 IMF 對應的能量為縱坐標，分別畫出信噪比高、低兩種情況下的能量曲線，見圖2～3。可見在信噪比高的情況下，IMF 分量的能量曲線會出現極小值點 ；在信噪比低的情況下，IMF 分量的能量曲線單調遞減，沒有出現極小值點。

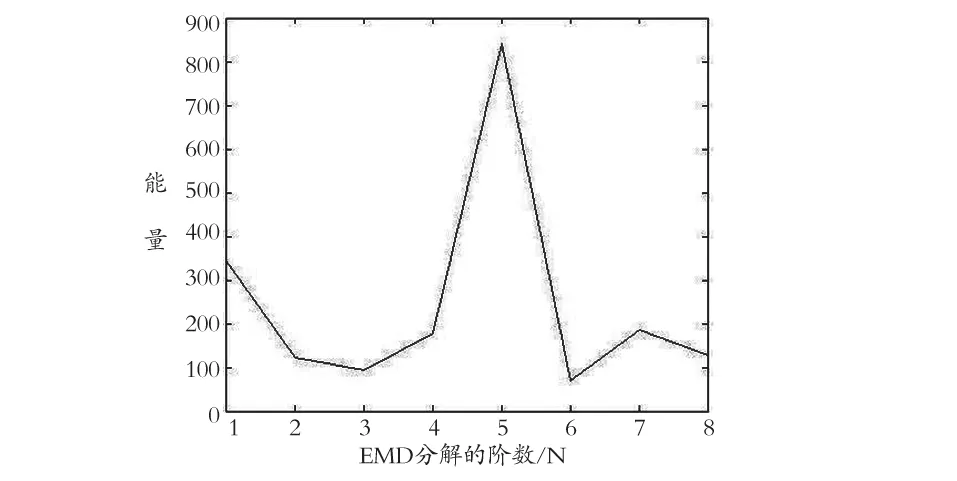
圖2 高性噪比下IMF分量能量曲線

圖3 低性噪比下IMF分量能量曲線

信噪比低的情況下，無法通過尋找 IMF 分量能量曲線極小值點的方法來確定噪聲占主導模態部分與有用信號占主導模態部分的分界點，此時引入基于噪聲與信號自相關函數特性差異的方法來確定該分界點。

自相關函數是信號時域特性的平均度量，描述了隨機信號x(t)在任意不同時刻t1和t2取值間的相關程度，一般定義為：

下面對比噪聲強度為 3 dBW 的高斯白噪聲n(t)與信號y(t) 的自相關函數（圖 4）：

y(t)= 5×sin ( 2×pi×0.2×t+6 )+10×sin ( 2×pi×1×t+10 )

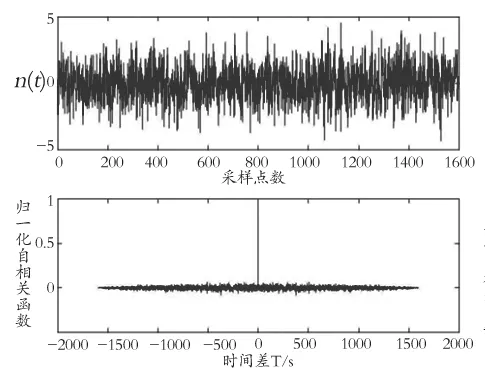
圖4 噪聲n(t)與信號y(t)及各自的自相關函數

由圖可見，高斯白噪聲n(t)由于其隨機性以及各時刻的弱相關性，自相關函數在零點出現了最大值，而其他點的值則迅速衰減 ；信號y(t)的自相關函數在零點出現了最大值，由于信號間存在相關性，因此其他點的值并未迅速衰減，而是隨著信號變化而變化。噪聲與信號通常都是夾雜在一起的，生物雷達回波信號也是如此。IMF 分量中噪聲占主導模態部分的自相關函數特性近似于高斯白噪聲n(t)，但沒有那么明顯 ；有用信號占主導模態部分的自相關函 數 的 統 計 特 性 則 近 似 于 信 號 y(t)。通過 IMF 分 量 自 相 關函數呈現出來的特性即可判定它是噪聲占主導模態還是有用信號占主導模態。

基于噪聲與信號自相關函數特性差異的分析方法處理步驟如下：

① 對 雷 達 回 波 信 號x(t)進 行 EMD 分 解， 得 到 n 個IMF 分 量 ；② 分 別 計 算 每 一 階 IMF 分 量 的 自 相 關 函 數xcorr(τ)=E [ IMFi(t) IMFi( t+τ) ]；③ 根據 IMF 分量自相關函數呈現的特點，判斷 IMF 分量中噪聲占主導模態部分與信號占主導模態部分的分界點k；④ 對噪聲占主導模態部分 的 IMF1～IMFk進行小波軟閾值去噪處理[14]，提取該部 分中包含的有用人體信息，得到 處理后的分 量 IMF1'～IMFk'，即 為 該 部 分 中 包 含 的 有 用 信 息 ；⑤ 將 IMF1'～IMFk'與信 號 占 主 導 模 態 部 分 的 IMFk～IMFN相 加 得 到 信 號 x(t)'：，即為最終經過噪聲抑制后的信號。

3 實驗測試

（1）實驗目標 ：與 UWB 生物雷達（型號為 SJ-3000）相隔一面實驗室穿單墻（厚度 28 cm），正對 UWB 雷達的人體。

（2）實驗預處理：為了減少運算量以及提高信噪比，對原始數據進行了空域積累與背景去除，經過積累與去背景的預處理后，信號中仍夾雜有大量高頻噪聲，需要對其進行去噪處理。

（3）實驗結果。對采集到的生物雷達回波信號經過預處理后的一個信噪比較低的點信號進行EMD分解，得到9個 IMF 分量。IMF 分量的能量曲線，見圖 5。

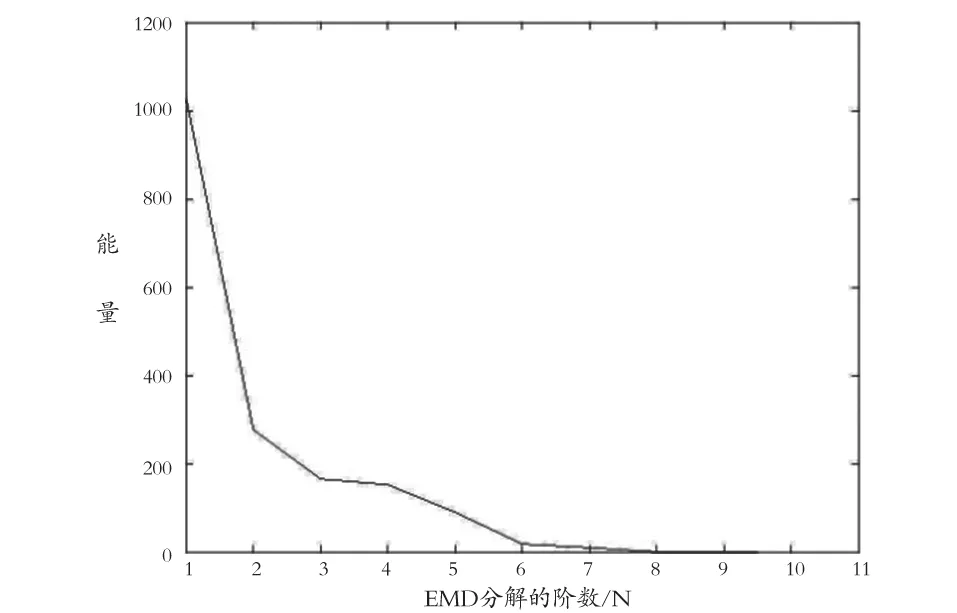
圖5 低信噪比信號IMF分量的能量曲線

由圖 5 可見 IMF 分量的能量曲線單調遞減，未出現極小值點，故需要采用基于噪聲與信號自相關函數特性差異的方法來進行噪聲處理。

分別求得 9 個 IMF 分量的自相關函數，發現前 4 階IMF 的自相關函數呈現出噪聲特性；從第 5 階 IMF 分量開始，自相關函數呈現信號特性，因此認為前 4 階 IMF 為噪聲占主導模態，5～9 階 IMF 為有用信號占主導模態，這樣就確定出了分界點k=5。按照前面敘述的步驟對信號進行處理，結果見圖6，有效去除了雷達回波信號中夾雜的高頻噪聲，保留了低頻有用人體信息。對其進行 FFT 頻譜分析，結果見圖7，可見信號中的高頻成分得到了有效抑制，低頻成分得以保留，達到了抑制高頻噪聲干擾的目的。

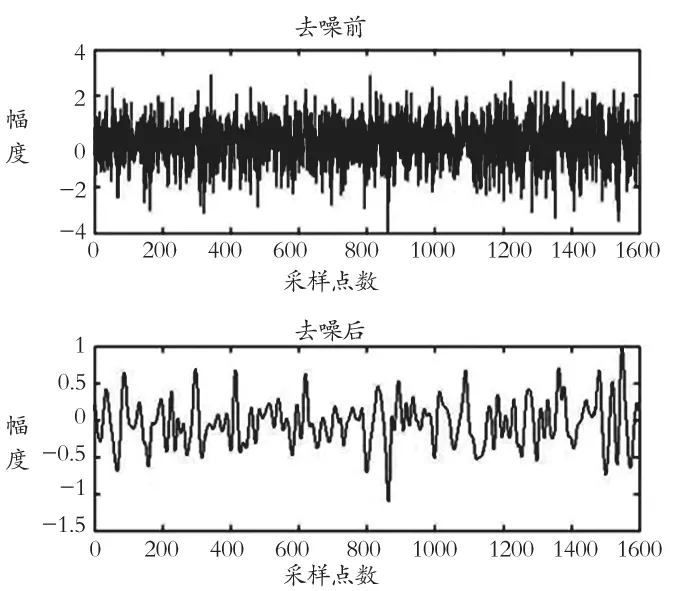
圖6 原信號與去噪后的信號

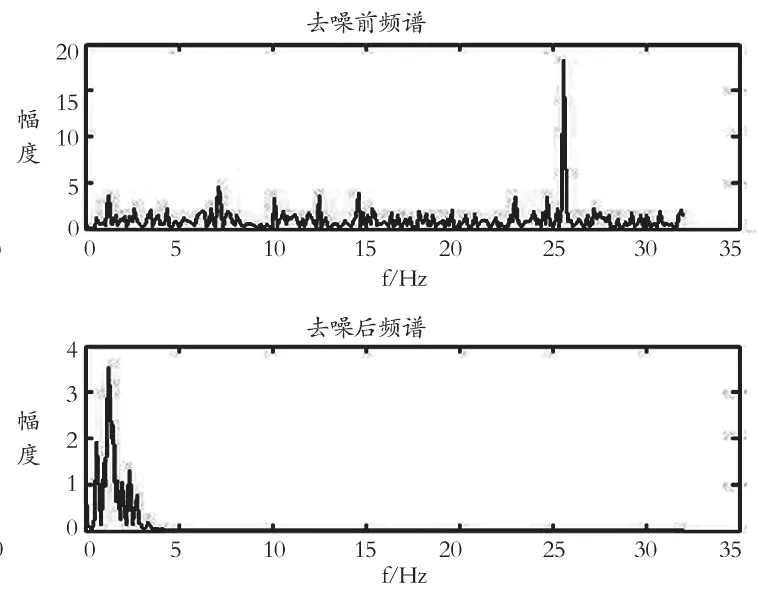
圖7 信號去噪前后的FFT譜分析

4 討論

對于信噪比較低的信號，通過基于噪聲與信號自相關函數特性差異的分析方法有效地去除了高頻噪聲成分，保留了低頻有用信息，且整個過程都以雷達回波信號經EMD分解得到的 IMF 分量的自相關函數特性為依據，未引入主觀參數，體現了該方法的自適應性。雖然該方法取得了一定效果，但還需要進一步的改進與細化，噪聲占主導模態部分與信號占主導模態部分的自相關函數特性都具有明顯的特性，但是兩部分可能會出現混疊的情況，即某一 IMF分量的自相關函數特性同時呈現出噪聲與信號特性，對于該情況的劃分還需進一步進行研究。

[1] 王健琪,鄭崇勛,路國華,等．雷達式生命探測儀中人體與動物識別技術的研究[J]．生物醫學工程學雜志,2005,22(6):1161-1164．

[2] Chen Kun-mu,Misra D,Wang Hui,et al．An X-Band microwave lifedetection system[J]．IEEE Trans Biomed End,1986,33(7):697-701．

[3] Staderini EM．UWB radars in medicine[J]．IEEE Aerospace and Electronic Systems Magazine,2002,17(1):13-18．

[4] Yarovoy AG,Ligthart LP,Matuzas J,et al．UWB radar for human being detection[J]．IEEE Aerospace and Electronic Systems Magazine,2006,21(3):10-14．

[5] 翟波,楊峰,孫水明,等．基于二維濾波的探地雷達數據去噪研究[J]．南京師范大學學報,2007,7(3):79-83．

[6] 司禎禎．傅里葉變換與小波變換在信號去噪中的應用[J]．電子設計工程,2011,19(4):155-157．

[7] Weiss LG．Wavelets and wideband correlation processing[J]．IEEE Signal Processing Magazine,1994,11(1):13-32．

[8] Baboli M,Ghorashi SA,Saniei N,et al．A new wavelet based algorithm respiratory motion rate using UWB radar[C]．Proc of International Conference on Biomedical and Pharmaoeutional Enginerring,Singapore,2009:1-3．

[9] N．E．Huang,Zhang Shen,Steven R Long,et al．The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]．Proc．R．Soc．Lond．A,1998,454(A):903-995．

[10] 樊迎迎．基于HHT算法的EEG信號分析與研究[D]．哈爾濱:哈爾濱理工大學,2012．

[11] 王健琪,薛慧君,呂昊,等．非接觸生理信號檢測技術[J]．中國醫療設備,2013,28(11):5-8,80．

[12] Lv Hao,Lu Guohua,Jing Xijin,et al．A new ultra-wideband radar for detecting survivors buried under earthquake rubbles[J]．Microwave and Optical Technology Letters,2010,52(11):2621-2642．

[13] Wu ZH,Huang NE．A study of the characteristics of white noise using the empirical mode decomposition method[J]．Proc．R．Soc．Lond．A,2004,460:1597-1611．

[14] Boudraa AO,Cexus JC,Saidi Z．EMD based signal noise reduction[J]．International Journal of Signal Processing,2004,(1):33-36．

Research on Noise Suppression of Bioradar Echo Signal Based on EMD

SUN Quan, ZHANG Yang, CAO Yang, WEN Zhong-yi
Department of Medical Administration, Navy General Hospital of PLA, Beijng 100048, China

ObjectiveTo suppress the noise of bioradar echo signal based on multiscale time-domain filtering features of empirical mode decomposition (EMD).MethodsEMD decomposition of preprocessed bioradar echo signal was conducted to obtain intrinsic mode functions (IMFs), which were divided into one mode with noise as its dominant components and the other mode with useful signal as its dominant components according to the differences of the features of noise and signal autocorrelation functions. Then the useful information of MIFs in the mode with noise as its dominant components extracted through the denoising method based on wavelet soft threshold was superimposed on MIFs in the mode with useful signal as its dominant components to obtain the life information of bioradar echo signal.ResultsThe high-frequency noise of bioradar echo signal has been fi ltered and the useful information of bioradar echo signal has been extracted with the noise suppression method based on EMD.ConclusionThe noise suppression method based on EMD can provide more useful information for the identify of organism objectives.

bioradar; empirical mode decomposition; intrinsic mode function; noise suppression

TN957.51

A

10.3969/j.issn.1674-163

1674-1633(2014)08-0025-04

2014-04-09

2014-06-23

作者郵箱：sunquan-007@163．com

3.2014.08.007