考慮初始幾何缺陷的大跨度上承式鋼管混凝土拱橋的非線性穩定研究

曾 勇，于 福，譚紅梅

(1.重慶交通大學山區橋梁結構與材料教育部工程研究中心，重慶 400074;2.重慶交通大學山區橋梁與隧道工程省部共建國家重點實驗室培育基地，重慶 400074;3.中交一航局第二工程有限公司，山東青島 266071)

鋼管混凝土拱橋按橋面在拱上的位置不同，分為上承式鋼管混凝土拱橋、中承式鋼管混凝土拱橋和下承式鋼管混凝土拱橋[1]。鋼管混凝土拱橋的主要受力構件以受壓彎為主，且鋼管混凝土拱橋隨著跨徑的增大，穩定問題更為突出。結構一旦發生失穩破壞，往往導致結構整體垮塌，帶來極大的損失，其危害性往往比強度破壞更大。目前，國內外學者對鋼管混凝土拱橋進行了廣泛研究，但這部分研究大都針對中、下承式鋼管混凝土拱橋，而對上承式鋼管混凝土拱橋研究較少，目前僅見于文獻[2-3]，但文獻[2]未研究非線性穩定。本文結合凈跨430 m的某鋼管混凝土拱橋，針對該橋跨度大、橫向剛度較弱的特點，研究了上承式鋼管混凝土拱橋的第二類穩定問題，得出了一些對設計和科研有意義的結論。

1 計算理論

在鋼管混凝土工程實踐中，恒載壓力線與拱軸線的偏離、施工預拱度的設置、施工偏差導致的初始變形、非對稱加載等因素使拱橋的失穩形態大部分屬于第二類失穩。鋼管混凝土拱橋隨跨徑的增大、材料強度的提高，在第二類失穩破壞時結構表現出大位移、大應變的特點，在實際試驗研究中充分說明這一點[4]。因此在對鋼管混凝土拱橋進行有限元分析時，應考慮結構的幾何非線性、材料非線性，或雙重非線性。拱的幾何非線性屬于彈性大變形問題，采用全量方法求解概念明確，易于理解。

拱橋結構的非線性平衡方程可寫為[5]

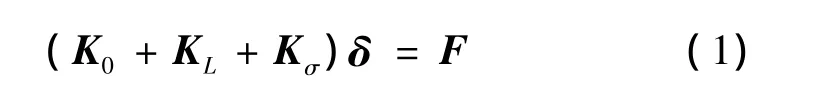
式中:K0為小位移線性剛度矩陣;KL為大位移矩陣;Kσ為初應力矩陣;δ為節點位移;F為等效節點荷載。另外，KL和Kσ是δ的函數，因此式(2)為非線性方程組。

非線性方程組的求解一般采用荷載增量法。荷載從0開始，按照某種增量形式逐步增大到λiF。當δ開始發散時，λiF即為拱橋極限承載力，可用Euler法，自修正Euler法等求解。如荷載增量步分得較細，可以偏于安全地認為前一級荷載為拱橋極限承載力，避免更加復雜的計算。

鋼結構的本構關系采用剛塑性本構關系，現行鋼橋設計規范對二類穩定安全系數尚沒有明確規定。根據失穩破壞不得先于強度破壞的原則，采用邊緣纖維屈服準則得到的不考慮荷載分項系數的整體穩定安全系數，應該大于容許應力安全系數，即對于鋼結構最小穩定安全系數應該＞1.7。混凝土的應力應變本構關系[6]，按式(2)考慮，混凝土極限應變取0.003 5。

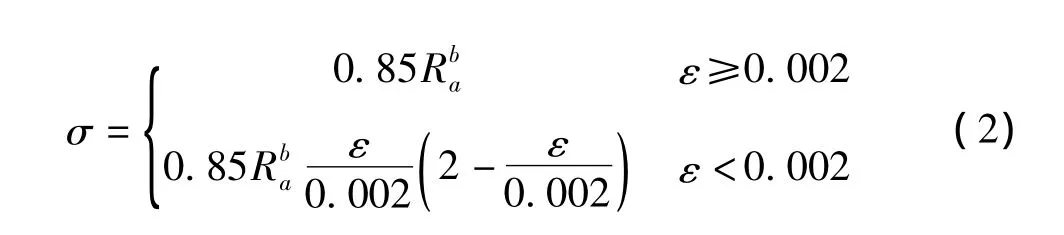
2 非線性穩定分析

2.1 工程概況

主拱圈采用鋼管混凝土與鋼管組成的桁架式斷面，斷面高度從拱腳13 m變化至拱頂6.5 m;單拱肋寬度4 m，由4根鋼管組成，兩單拱肋間中心距13 m。拱肋鋼管外徑1200 mm，最大管壁厚度35 mm。全橋立面圖和主梁截面布置圖分別見圖1和圖2。

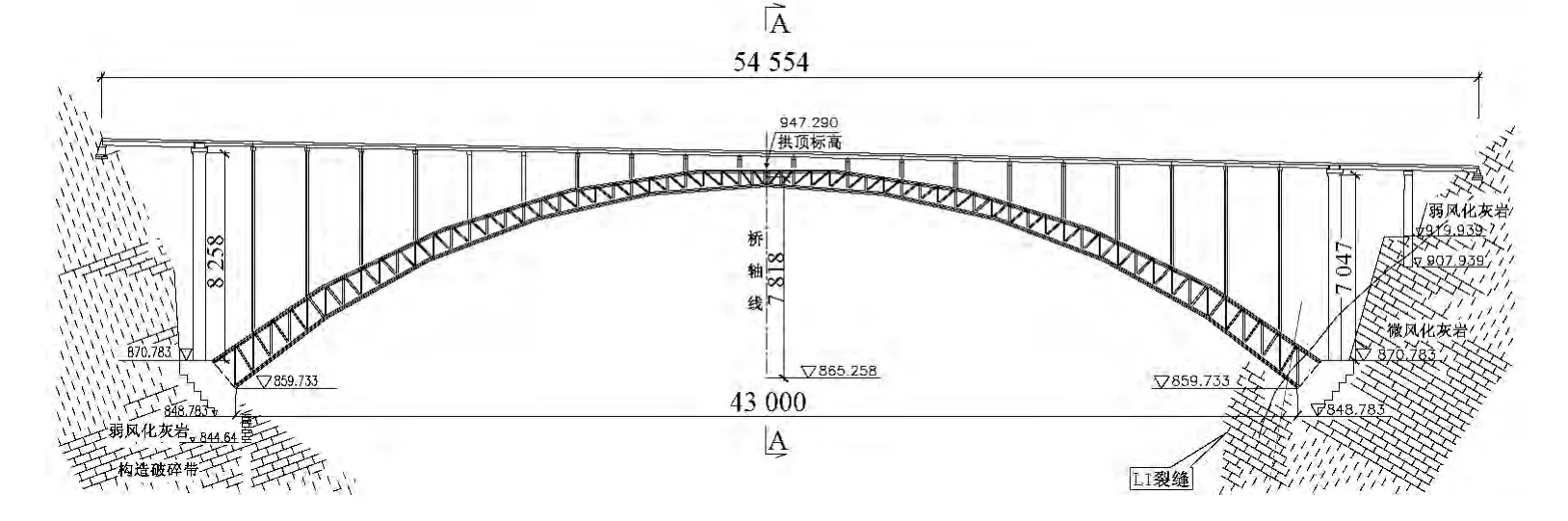
圖1 全橋立面(單位:cm)

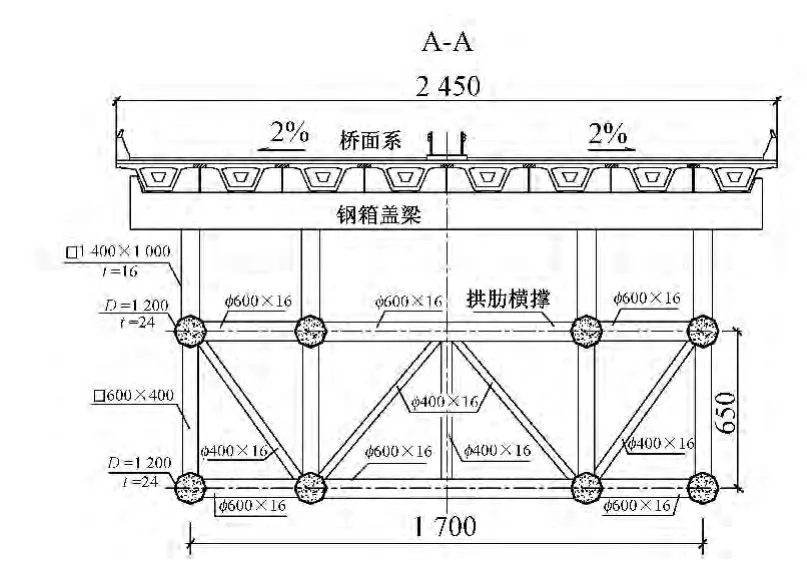
圖2 主梁截面(單位:cm)

鋼管混凝土拱肋截面由鋼管與混凝土兩種材料組成，本文不按換算截面法做等效轉換[1]，而是采用共用節點的分析模式，即將鋼管混凝土模擬成鋼管梁模型和混凝土梁模型，兩種梁模型采用公共節點，保證鋼管和混凝土的共同受力。

對于恒載，穩定系數定義為恒載的λ倍，即λg;對于活載則為相應活載的倍數，恒載不進行累加，即結構發生失穩時的荷載為g+λq。二類穩定分析采用的是考慮幾何非線性和材料非線性的靜力分析[7]。

2.2 計算工況

分析該橋成橋階段的第二類穩定，先不考慮初始幾何缺陷的影響，分為以下6種荷載工況:①橋梁恒載作用(工況1);②恒載+風荷載作用(工況2);③恒載+全跨滿布公路—Ⅰ級汽車荷載作用(工況3);④恒載+左半跨滿布公路—Ⅰ級汽車荷載作用(工況4);⑤恒載+右半跨滿布公路—Ⅰ級汽車荷載作用(工況5);⑥恒載+全跨半橋寬滿布公路—Ⅰ級汽車荷載作用(工況6)。

不考慮缺陷時各工況的分析結果見表1。

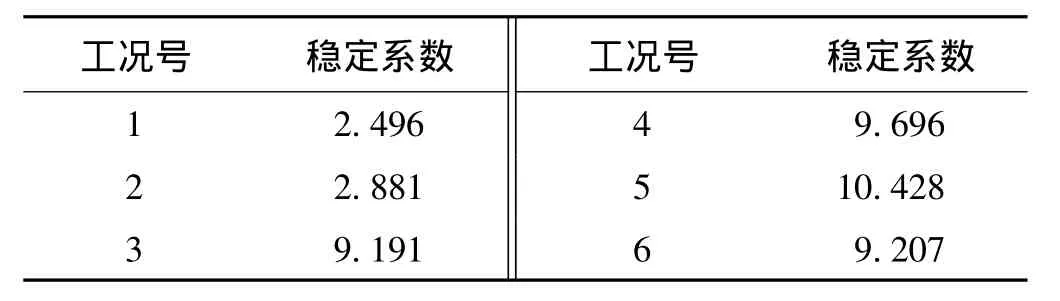
表1 不考慮缺陷的第二類穩定的穩定系數

3 考慮初始幾何缺陷的非線性穩定分析

由于在制造、運輸及安裝等各施工環節中，拱肋會產生一定的變形，鋼管成拱后的拱軸線往往達不到理想拱軸線，即拱肋存在初始的偏差。同時在結構自重及外荷載作用下，拱肋會產生附加的內力和變形。所以在鋼管混凝土拱橋的建造過程中，不可避免地存在著初始幾何缺陷。

穩定性分析考慮初始缺陷的大小為:第一種情況正對稱初始幾何缺陷，主拱圈橫向偏移半個正弦波，最大位移為0.15 m。第二種情況反對稱初始幾何缺陷，主拱圈橫向偏移一個正弦波，最大位移為0.15 m。考慮偏心的非線性穩定分析采用的假定和失穩判別準則同上節一致。在成橋階段，對主橋結構進行第二類穩定分析，分別考慮正、反對稱缺陷的影響，考慮的荷載工況與一類穩定一樣。

在成橋階段，對主橋結構進行第二類穩定分析，分別考慮正、反對稱缺陷的影響，分為12種荷載工況。各種工況下二類穩定系數對比見表2。典型工況作用下的二類穩定失穩形態見圖3。

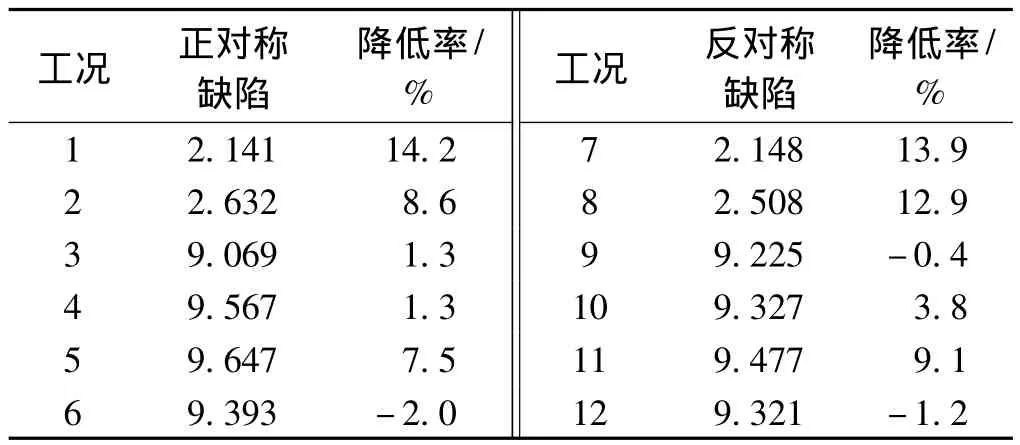
表2 各種工況下二類穩定系數對比

從表2和圖3可以看出，考慮了正、反對稱偏心后，會降低結構的穩定系數。初始幾何缺陷削弱了結構的剛度，增大了拱橋的初始幾何缺陷彎矩。對應于工況1，初始幾何偏心缺陷降低了拱橋結構的穩定性。不考慮初始幾何偏心缺陷，穩定系數越低的工況，初始幾何偏心缺陷則降低穩定系數的比例越少。但有趣的是，對于工況6，初始幾何缺陷使得結構的穩定性有所提高，主要原因是施加初始幾何缺陷的方向與全橋半幅汽車加載的方向相反，起著有利的作用。如果偏心施加的方向與全橋半幅汽車加載方向相同，穩定系數則會降低。

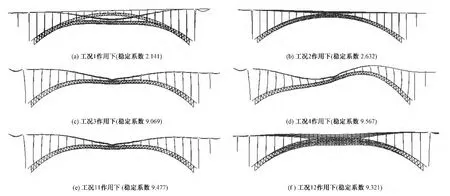
圖3 第二類失穩形態示意

4 結論

1)通過考慮有正、反對稱初始幾何缺陷的第二類穩定分析，該大跨度上承式鋼管混凝土拱橋在不同的工況下穩定系數均＞2，滿足相應的規范要求。

2)非線性因素對大跨度上承式鋼管混凝土拱橋的穩定性影響顯著，考慮非線性因素才能求得真正的穩定系數。各工況下結構的失穩形態與自重荷載工況類似，主要原因是結構自重為主要荷載，其它荷載的作用效應均小于自重引起的荷載效應。

3)考慮了正、反對稱幾何初始缺陷后，會降低結構的穩定系數。初始幾何缺陷削弱了結構的剛度，同時也加大了荷載引起的初始幾何缺陷彎矩，應當引起重視。

4)雖然正、反對稱偏心不會改變結構的失穩形態，但會在一定程度上降低結構的穩定系數。

[1]陳寶春.鋼管混凝土拱橋設計與施工[M].北京:人民交通出版社，2000.

[2]趙河清，徐亮，楊惠林，等.大跨度上承式鋼管混凝土拱橋的穩定性分析[M].公路交通科技，2006(11):82-85.

[3]曾勇，馬如進，陳艾榮.大跨度上承式鋼管混凝土拱橋的非線性穩定分析[J].上海公路，2008(2):50-53，64.

[4]項海帆.高等橋梁結構理論[M].北京:人民交通出版社，2001.

[5]李國豪.橋梁結構穩定與振動[M].北京:中國鐵道出版社，1996.

[6]過鎮海.混凝土的強度和本構關系——原理與應用[M].北京:中國建筑工業出版社，1999.

[7]張興春.鋼管混凝土系桿拱橋施工關鍵技術及整體穩定性分析[J].鐵道建筑，2012(8):5-7.