(2+1)維五次非線性薛定諤方程的無窮序列新解

阿如娜,套格圖桑

(內蒙古師范大學數學科學學院,呼和浩特 010022)

(2+1)維五次非線性薛定諤方程的無窮序列新解

阿如娜,套格圖桑

(內蒙古師范大學數學科學學院,呼和浩特 010022)

利用第二種橢圓方程的解和B¨acklund變換,獲得了(2+1)維五次非線性薛定諤方程的新解.這些解是由Jacobi橢圓函數、三角函數、Riemann theta函數和指數函數組成的無窮序列新解.

第二種橢圓方程;B¨acklund變換;無窮序列新解

1 引言

許多文獻研究不同設置下自聚焦和自散焦非線性時空效應[13].如鎖模激光器[4],光纖和波導的脈沖傳播[5],激光等離子體相互作用[67].物理學中許多現象是由非線性偏微分方程(NPDES)描述的.尋找非線性偏微分方程的解是解釋其描述的自然現象的最有效方法之一.

(2+1)維五次非線性薛定諤方程[8](CQNLSE):

這里x和z是橫向和傳播坐標,t是所謂的減少時間.(2+1)維五次非線性薛定諤方程,是描述多種物理系統的數學模型.文獻[8-9]給出了CQNLSE方程的一些固定解.

本文對(2+1)維五次非線性薛定諤方程進行了行波變換后,利用第二種橢圓方程的已知解和B¨acklund變換,獲得了(2+1)維五次非線性薛定諤方程的無窮序列解,這些解包括Jacobi橢圓函數、三角函數、Riemann theta函數和指數函數解.

2 (2+1)維五次非線性薛定諤方程的解

對(2+1)維五次非線性薛定諤方程(1)作變換:

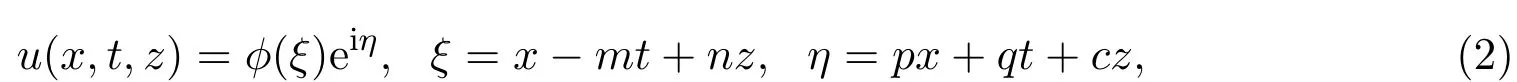
這里m,n,p,q和c是待定常數.

將(2)式代入方程(1),化簡后得到如下常微分方程:

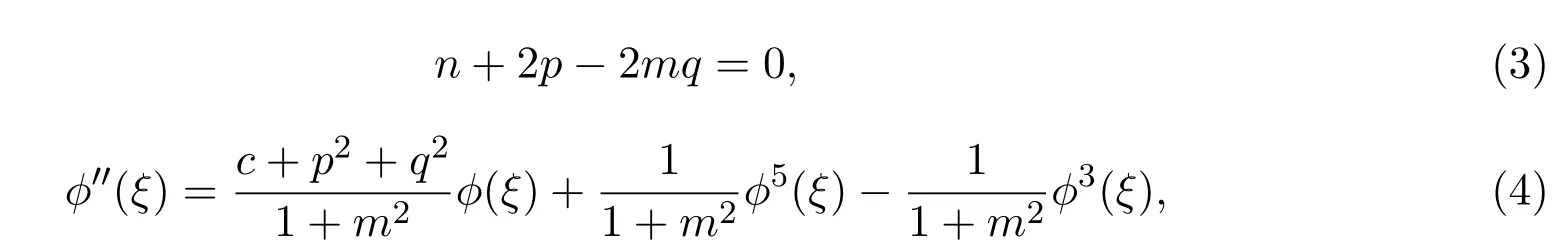
用?′(ξ)乘方程(4)的兩邊,并對ξ積分一次后得到下列方程:

這里k是積分常數.

利用函數變換φ(ξ)=?2(ξ),把方程(5)轉化為下列常微分方程:

在方程(6)中取

這里g1,g2,g3,g4和g5是任意常數,其中z(ξ)滿足下列第二種橢圓方程:

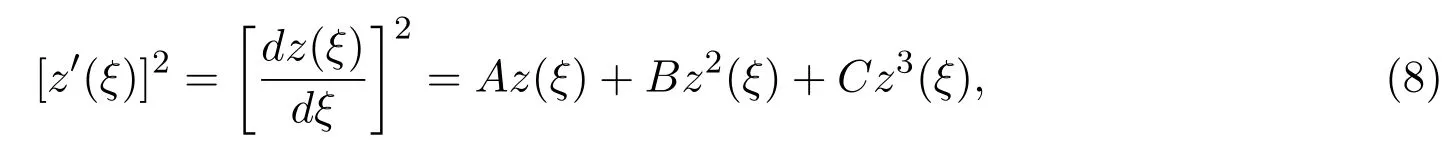
將(7)和(8)式一起代入(6)式,并令zi(ξ)(i=0,1,2,···,7)的系數為零后得到下列非線性代數方程組

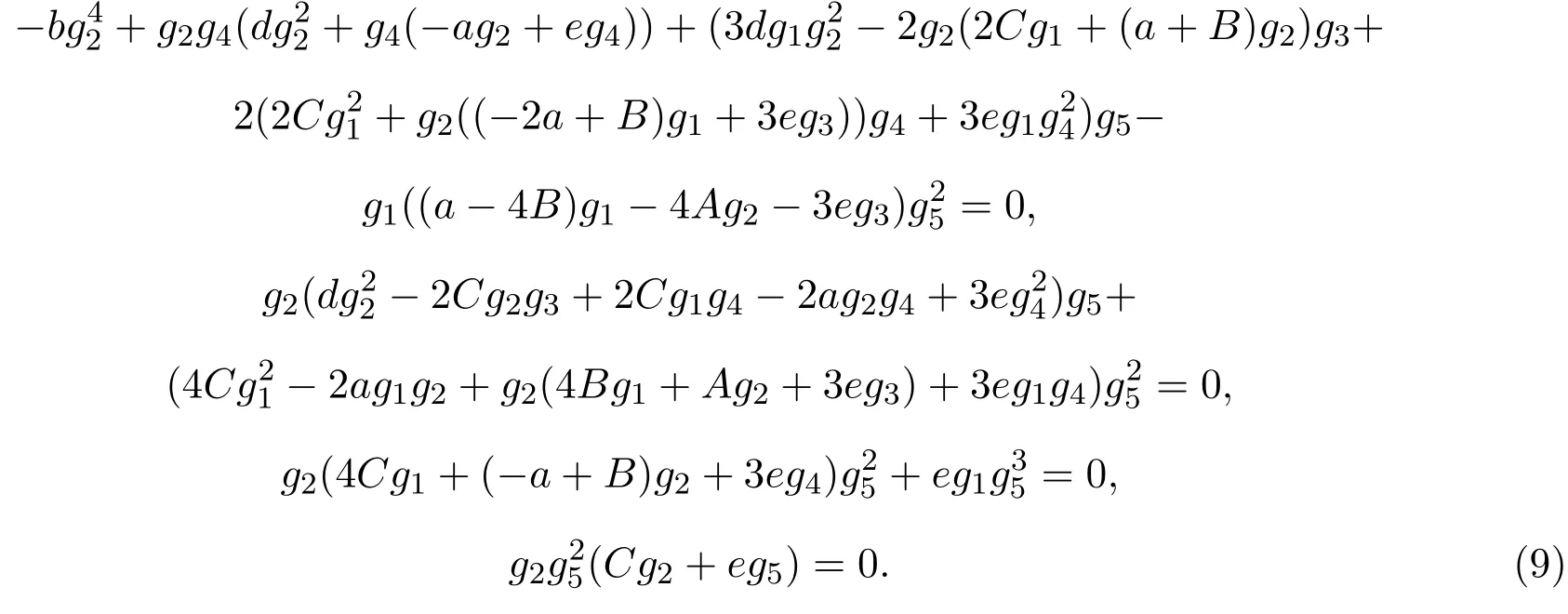
用符號計算系統Mathematica求出該方程組的下列解:

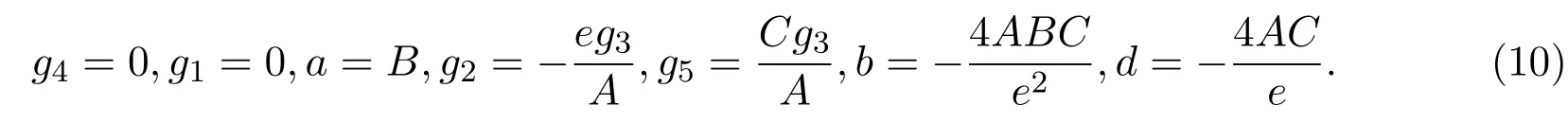
其中,A,B,C,e和g3為不全為零的任意常數,A,B和C是方程(8)的系數.

將(10)式代入(7)式后,得到方程(6)的下列形式解:

其中e為任意常數,A和C是方程(8)的系數,z(ξ)滿足方程(8).

由形式解(11)和φ(ξ)=?2(ξ)得到方程(4)的下列解:這里e為任意常數,A和C是方程(8)的系數,z(ξ)滿足方程(8).

2.1 第二種橢圓方程的解

2.1.1 第二種橢圓方程 (8)的Jacobi橢圓函數解

文獻[10]中獲得了方程(8)的如下解:

當A=4,B=?4(1+k2),C=4k2時,(13)式是第二種橢圓方程(8)的解:

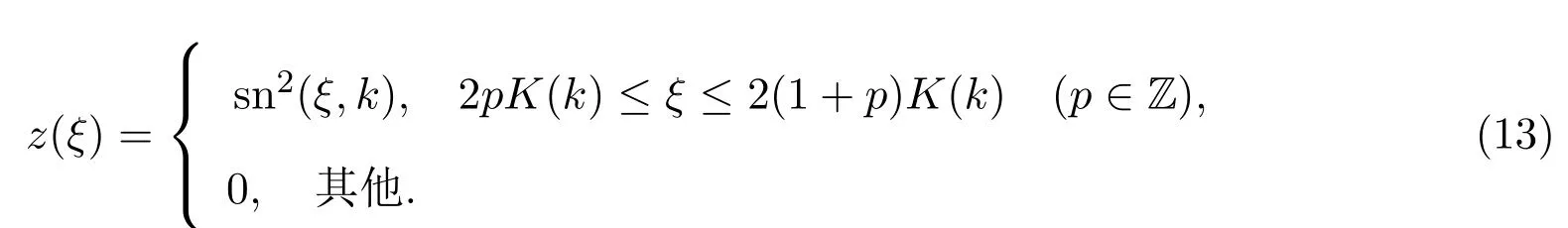
當A=4(1?k2),B=4(2k2?1),C=?4k2時,獲得第二種橢圓方程(8)的如下解:

2.1.2 第二種橢圓方程(8)的Riemann theta函數新解

(15)式為 Riemann theta函數的定義,文獻 [10]中獲得了第二種橢圓方程 (8)的如下Riemann theta函數:

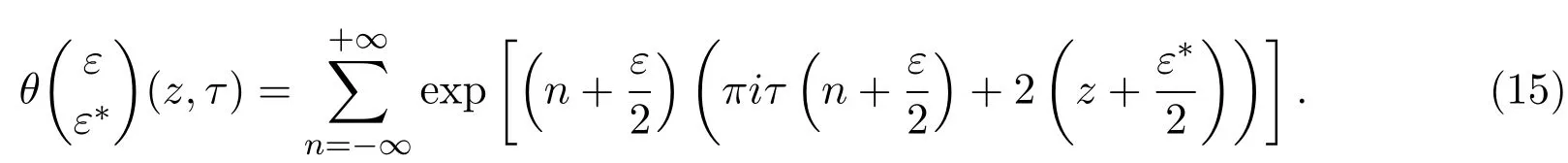
2.1.3 第二種橢圓方程 (8)的三角函數型解

由文獻[10]可得到第二種橢圓方程(8)的如下三角函數解.

當C=0時,得到第二種橢圓方程(8)的下列解:

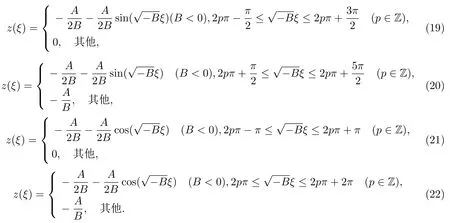
2.1.4 第二種橢圓方程 (8)的指數函數型解

文獻[11]給出了方程(8)的下列解.

當B2?4AC=0時,可得到第二種橢圓方程(8)的下列解:

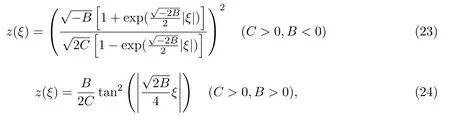
當A=C=0時,經計算獲得第二種橢圓方程(8)的如下解:

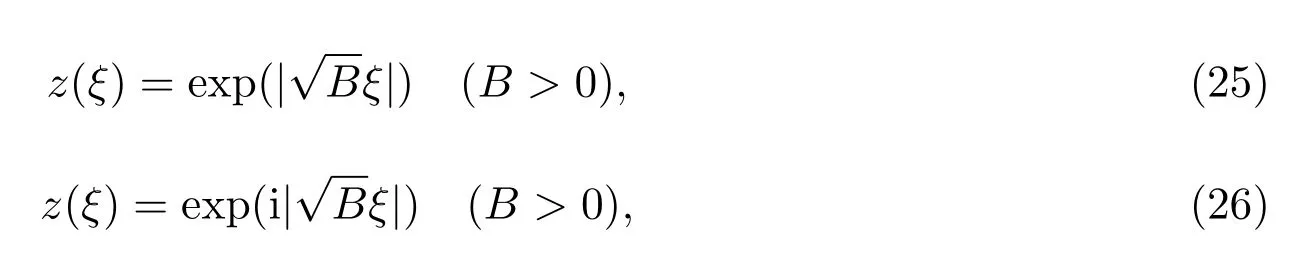
當A=0時,可得到第二種橢圓方程(8)的如下解:

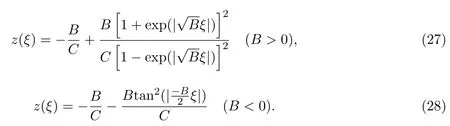
2.2 第二種橢圓方程的B¨acklund變換

由文獻[11]可知,如果zr?1(ξ)是第二種橢圓方程(8)的解,則下列zr(ξ)也是第二種橢圓方程(8)的解.

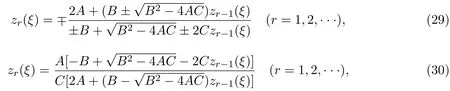
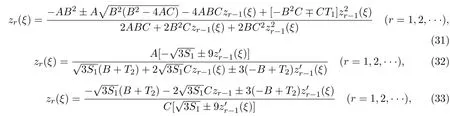
其中

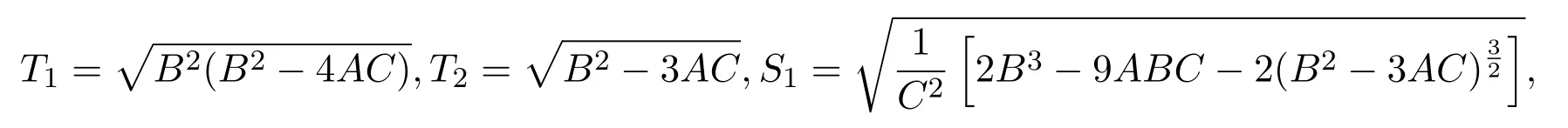
A,B和C是第二種橢圓方程(8)的系數.

情形 1(2+1)維五次非線性薛定諤方程的Jacobi橢圓函數型無窮序列解

將(13)式(或(14)),(12)式和(29)式代入(2)式,可得到(2+1)維五次非線性薛定諤方程的Jacobi橢圓函數型無窮序列解.

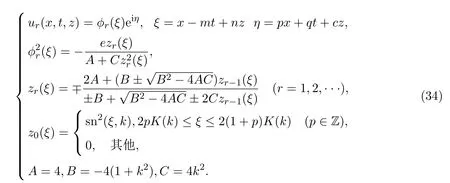
其中

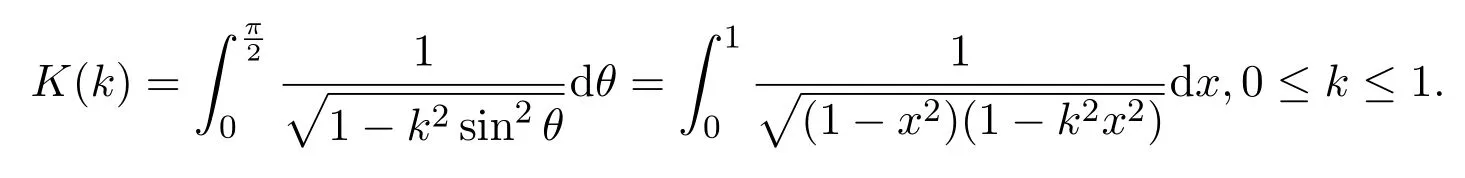
情形 2(2+1)維五次非線性薛定諤方程的三角函數型無窮序列解

通過下列疊加公式,可獲得(2+1)維五次非線性薛定諤方程的三角函數型無窮序列解.

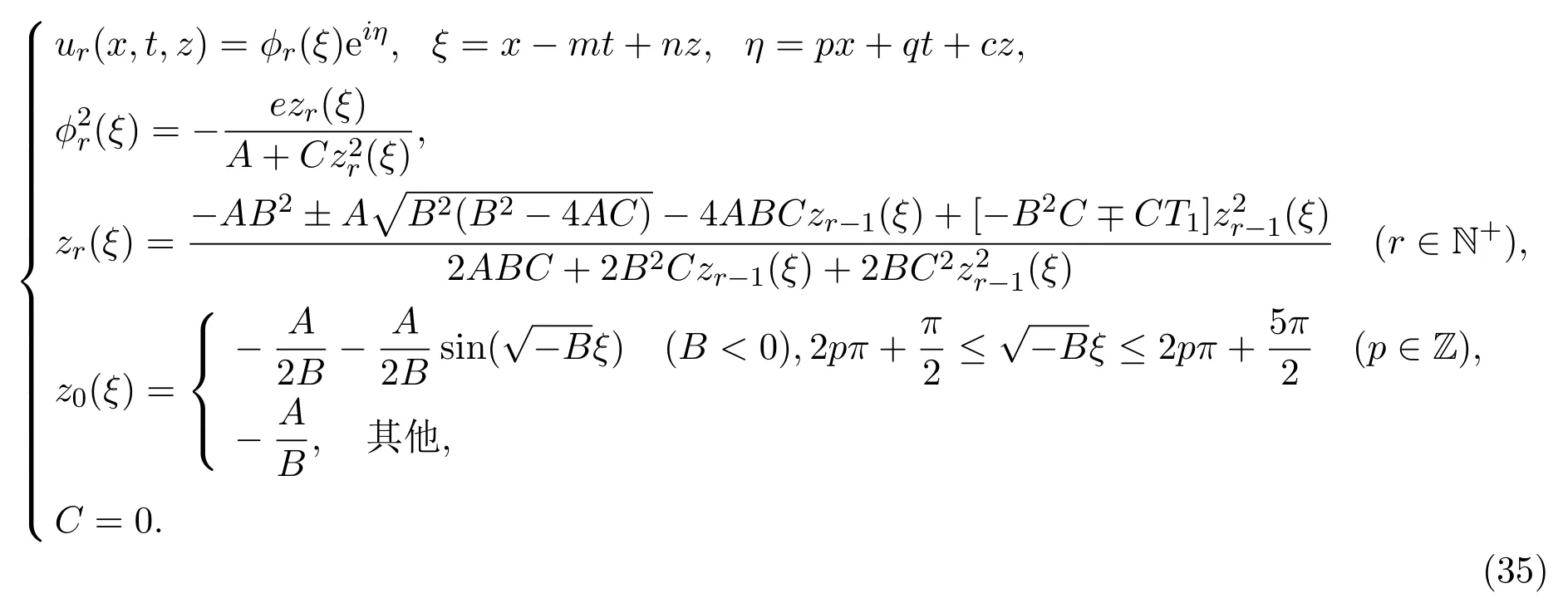
情形 3(2+1)維五次非線性薛定諤方程的指數函數型無窮序列解

由以下迭代公式,可構造(2+1)維五次非線性薛定諤方程的指數函數型無窮序列解.

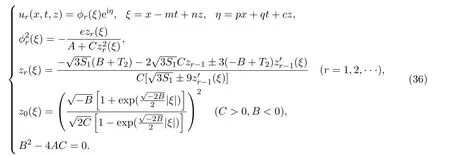
情形 4(2+1)維五次非線性薛定諤方程的Riemann theta函數型無窮序列解

通過以下公式,可獲得(2+1)維五次非線性薛定諤方程的Riemann theta函數型無窮序列解.

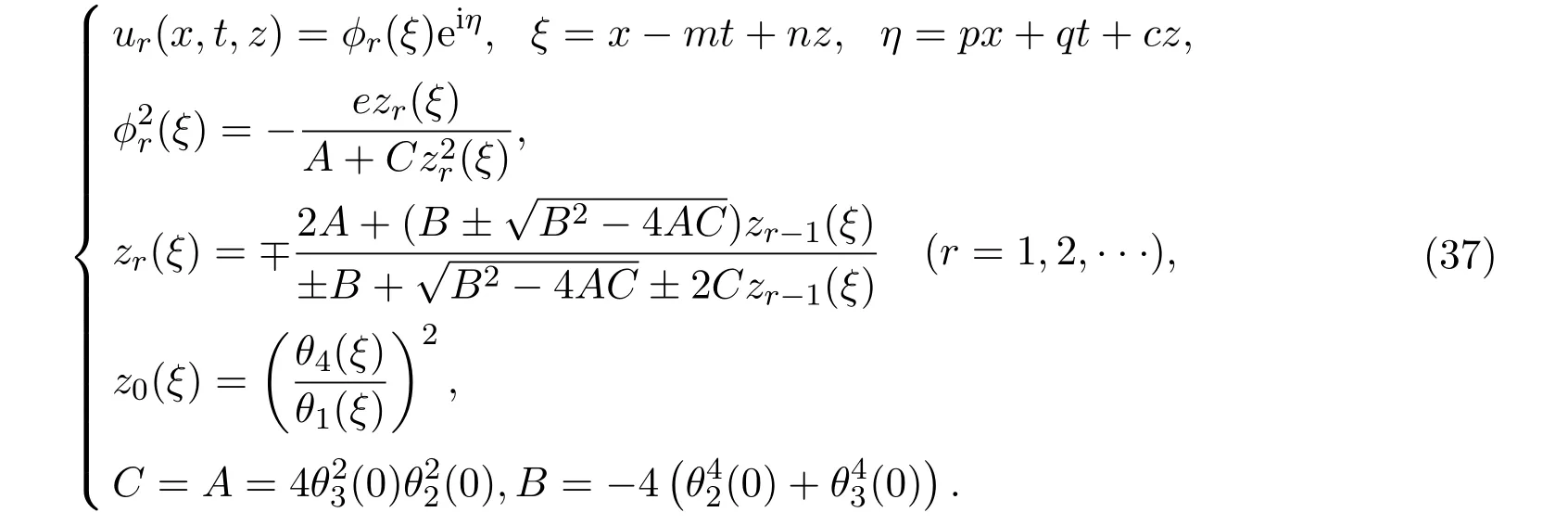
在以上的(34)-(37)式中,n,m,p,q是滿足方程(3)的任意常數,A,B和C是方程(8)的系數.

3 結論

文獻[12]獲得了(2+1)維五次非線性薛定諤方程的雙曲函數型和Jacobi橢圓函數型有限多個新解.本文利用行波變換、第二種橢圓方程的解和B¨acklund變換,構造了(2+1)維五次非線性薛定諤方程的由Jacobi橢圓函數、三角函數、Riemann theta函數和指數函數組成的無窮序列新解,所獲得的解包括文獻[12]所獲得解.例如:文獻[12]得到了方程(1)的下列形式解:

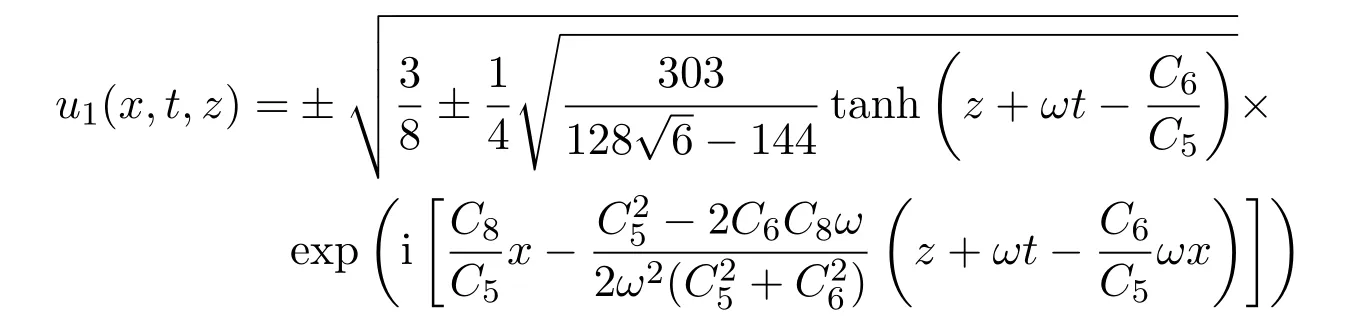
在迭代公式(34)中,當k→1時,sn(ξ,k)→tanh(ξ),便可得到方程(1)形如u1(x,t,z)的解.

參考文獻

[1] Towers I N,Malomed B A,Wise F W.Light bullets in quadratic media with normal dispersion at the second harmonic[J].Phys.Rev.Lett.,2003,90:123902.

[2] Mihalache D,Mazilu D,Towers I,et al.Stable spinning optical solitons in three dimensions[J].Phys.Rev. Lett.,2002,88:073902.

[3] Mihalache D,Mazilu D,Lederer F,et al.Stable vortex tori in the three-dimensional cubic-quintic Ginzburg-Landau equation[J].Phys.Rev.Lett.,2006,97:073904.

[4] Moores J D.On the Ginzburg-Landau laser mode-locking model with fi fth-order saturable absorber term[J]. Opt.Commun.,1993,96:65-70.

[5] Mihalache D,Mazilu D,Bertolotti M,et al.Exact solution for nonlinear thin- fi lm guided waves in higherorder nonlinear media[J].J.Opt.Soc.Am.B,1988,5:565-570.

[6] Chen Y X,Lu X H.Spatiotemporal similaritons in(3+1)-dimensional inhomogeneous nonlinear medium with cubic-quintic nonlinearit[J].Commun.Theor.Phys.,2011,55:871-877.

[7] Liu H,Beech R,Osman F,et al.Periodic and solitary waves of the cubic-quintic nonlinear Schr¨odinger equation[J].J.Plasma Phys.,2004,70:415-429.

[8] Malomed B A,Crasovan L C,Mihalache D.Stability of vortex solitons in the cubic-quintic model[J]. Physica.D,2002,161:187-201.

[9] Quiroga-Teixeiro M,Michinel H.Stable azimuthal stationary state in quintic nonlinear optical media[J].J. Opt.Soc.Am.B,1997,14:2004-2009.

[10] 套格圖桑,白玉梅.非線性發展方程的Riemann theta函數等幾種新解[J].物理學報,2013,62(10):100201.

[11] 套格圖桑.論非線性發展方程求解中輔助方程法的歷史演進[M].北京:中央民族大學出版社,2012,6:251-255.

[12] Guo A L,Lin J.(2+1)-dimensional analytical solutions of the combining cubic-quintic nonlinear Schr¨odinger equation[J].Commun.Theor.Phys.,2012,57:523-529.

New in fi nite sequence solutions of(2+1)-dimensional cubic-quintic nonlinear Schr¨odinger equation

Aruna,Taogetusang
(College of Mathematical Science,Inner Mongolia Normal University,Huhhot 010022,China)

In order to obtain a new in fi nite sequence solutions of(2+1)-dimensional cubic-quintic nonlinear Schr¨odinger equation,this paper uses the solutions and B¨acklund transform of second kind of elliptic equations to construct the new in fi nite sequence solutions of(2+1)-dimensional cubic-quintic nonlinear Schr¨odinger equation consisting of Jacobi elliptic function,trigonometric function,Riemann theta function and exponential function.

the second kind of elliptic equation,B¨acklund transform,new in fi nite sequence solutions

O175.29

A

1008-5513(2014)04-0412-08

10.3969/j.issn.1008-5513.2014.04.011

2014-05-11.

國家自然科學基金(11361040);內蒙古自治區高等學校科學研究基金(NJZY12031);內蒙古自治區自然科學基金(2010MS0111).

阿如娜(1991-),碩士生,研究方向：孤立子與可積系統理論及其應用.

2010 MSC:35Q51